One extent of space research is seen in the Mars Opportunity mission
The first major scientific discovery made from space was the dangerous Van Allen radiation belts
Space research is scientific study carried out in outer space, and by studying outer space. From the use of space technology to the observable universe, space research is a wide research field. Earth science, materials science, biology, medicine, and physics all apply to the space research environment. The term includes scientific payloads at any altitude from deep space to low Earth orbit, extended to include sounding rocket research in the upper atmosphere, and high-altitude balloons.
Space exploration is also a form of space research.
History
The first US satellite was the Explorer 1, seen here launching, 1st February 1958
First image of the far side of the Moon, sent back to Earth by the Luna 3 mission
Rockets
The Chinese used rockets in ceremony and as weaponry since the 13th century, but no rocket would overcome Earth's gravity
until the latter half of the 20th century. Space-capable rocketry
appeared simultaneously in the work of three scientists, in three
separate countries. In Russia, Konstantin Tsiolkovski, in the United States, Robert Goddard, and in Germany, Hermann Oberth.
The United States and the Soviet Union
created their own missile programs. The space research field evolved as
scientific investigation based on advancing rocket technology.
In 1948–1949 detectors on V-2 rocket flights detected x-rays from the Sun. Sounding rockets helped show us the structure of the upper atmosphere. As higher altitudes were reached, space physics emerged as a field of research with studies of Earths aurorae, ionosphere and magnetosphere.
Artificial satellites
The first artificial satellite, Russian Sputnik 1, launched on October 4, 1957, four months before the United States first, Explorer 1. The first major discovery of satellite research was in 1958, when Explorer 1 detected the Van Allen radiation belts. Planetology reached a new stage with the Russian Luna programme, between 1959 and 1976, a series of lunar probes
which gave us evidence of the Moons chemical composition, gravity,
temperature, soil samples, the first photographs of the far side of the
Moon by Luna 3, and the first remotely controlled robots (Lunokhod) to land on another planetary body.
Yuri Gagarin was the first passenger on a space flight, the Vostok 1, first flight of the Vostok programme
Astronauts
The early space researchers obtained an important international forum with the establishment of the Committee on Space Research
(COSPAR) in 1958, which achieved an exchange of scientific information
between east and west during the cold war, despite the military origin
of the rocket technology underlying the research field.
On April 12, 1961, Russian Lieutenant Yuri Gagarin was the first human to orbit Earth, in Vostok 1. In 1961, US astronaut Alan Shepard was the first American in space. And on July 20, 1969, astronaut Neil Armstrong was the first human on the Moon.
On April 19, 1971, the Soviet Union launched the Salyut 1,
the first space station of substantial duration, a successful 23 day
mission, sadly ruined by transport disasters. On May 14, 1973, Skylab, the first American space station launched, on a modified Saturn V rocket. Skylab was occupied for 24 weeks.
Interstellar
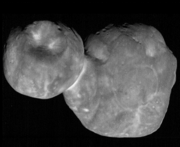
"Ultima Thule" (2014 MU69) is the farthest object visited by human spacecraft
"Ultima Thule"
is the nickname of the farthest and most primitive object visited by
human spacecraft. Originally named "1110113Y" when detected by Hubble in 2014, the planetessimal was reached by the New Horizons
probe on 1st January 2019 after a week long manoeuvering phase. New
Horizons detected Ultima Thule from 107 million miles and performed a
total 9 days of manoeuvres to pass within 3,500 miles of the 19 mile
long contact binary. Ultima Thule has an orbital period around 298 years, is 4.1 billion miles from Earth, and over 1 billion miles beyond Pluto.
Two Pioneer
probes and the New Horizons probe are expected to enter interstellar
medium, but these three are expected to have depleted available power
before then, so the point of exit cannot be confirmed precisely.
Predicting probes speed is imprecise as they pass through the variable heliosphere. Pioneer 10 is roughly at the outer edge of the heliosphere in 2019. New Horizons should reach it by 2040, and Pioneer 11 by 2060.
The Voyager 1 probe launched 41 years, 8 months and 18 days ago, and flew beyond the edge our solar system in August 2012 to the interstellar medium. The farthest human object from the Earth, predictions include collision, an Oort cloud, and destiny, "perhaps eternally—to wander the Milky Way."
Voyager 2
launched on 20th August 1977 travelling slower than Voyager 1 and
reached interstellar medium by the end of 2018. Voyager 2 is the only
Earth probe to have visited the ice giants of Neptune or Uranus.
Neither Voyager is aimed at a particular visible object. Both continue to send research data to NASA Deep Space Network as of 2019.
Two Voyager probes have reached interstellar medium, and three other probes are expected to join that list.
Research fields
Space research includes the following fields of science:
- Earth observations, using remote sensing techniques to interpret optical and radar data from Earth observation satellites
- Geodesy, using gravitational perturbations of satellite orbits
- Atmospheric sciences, aeronomy using satellites, sounding rockets and high-altitude balloons
- Space physics, the in situ study of space plasmas, e.g. aurorae, the ionosphere, the magnetosphere and space weather
- Planetology, using space probes to study objects in the planetary system
- Astronomy, using space telescopes and detectors that are not limited by looking through the atmosphere
- Materials sciences, taking advantage of the micro-g environment on orbital platforms
- Life sciences, including human physiology, using the space radiation environment and weightlessness
- Physics, using space as a laboratory for studies in fundamental physics.
Space research from artificial satellites
Upper Atmosphere Research Satellite
Upper Atmosphere Research Satellite was a NASA-led
mission launched on September 12, 1991. The 5,900 kg (13,000 lb)
satellite was deployed from the Space Shuttle Discovery during the STS-48
mission on 15 September 1991. It was the first multi-instrumented
satellite to study various aspects of the Earth's atmosphere and have a
better understanding of photochemistry. After 14 years of service, the UARS finished its scientific career in 2005.
Great Observatories program
Great Observatories program telescopes are combined for enhanced detail in this image of the Crab Nebula
Great Observatories program is the flagship NASA
telescope program. The Great Observatories program pushes forward our
understanding of the universe with detailed observation of the sky,
based in gamma rays, ultraviolet, x-ray, infrared, and visible, light spectrums. The four main telescopes for the Great Observatories program are, Hubble Space Telescope (visible, ultraviolet), launched 1990, Compton Gamma Ray Observatory (gamma), launched 1991, Chandra X-Ray Observatory (x-ray), launched 1999, and Spitzer Space Telescope (infrared), launched 2003.
Origins of the Hubble, named after American astronomer Edwin Hubble, go back as far as 1946. In the present day, the Hubble is used to identify exo-planets
and give detailed accounts of events in our own solar system. Hubbles
visible-light observations are combined with the other great
observatories to give us some of the most detailed images of the visible
universe.
International Gamma-Ray Astrophysics Laboratory
INTEGRAL is one of the most powerful gamma-ray observatories, launched by the European Space Agency
in 2002, and continuing to operate (as of March 2019). INTEGRAL
provides insight into the most energetic cosmological formations in
space including, black holes, neutron stars, and supernovas. INTEGRAL plays an important role researching gamma-rays, one of the most exotic and energetic phenomena in space.
Gravity and Extreme Magnetism Small Explorer
The NASA-led GEMS mission was scheduled to launch for November 2014.
The spacecraft would use an X-Ray telescope to measure the polarization
of x-rays coming from black holes and neutron stars. It would research
into remnants of supernovae, stars that have exploded. Few experiments
have been conducted in X-Ray polarization since the 1970s, and
scientists anticipated GEMS to break new ground. Understanding x-ray
polarisation will improve scientists knowledge of black holes, in
particular whether matter around a black hole is confined, to a
flat-disk, a puffed disk, or a squirting jet. The GEMS project was
cancelled in June 2012, projected to fail time and finance limits. The
purpose of the GEMS mission continues to be relevant (as of 2019).
Space research on space stations
Russian station Mir was the first long term inhabited station
Salyut 1
Salyut 1 was the first space station ever built. It was launched in April 19, 1971 by the Soviet Union.
The first crew failed entry into the space station. The second crew was
able to spend twenty-three days in the space station, but this
achievement was quickly overshadowed since the crew died on reentry to
Earth. Salyut 1 was intentionally deorbited six months into orbit since
it prematurely ran out of fuel.
Skylab
Skylab
was the first American space station. It was 4 times larger than Salut
1. Skylab was launched in May 19, 1973. It rotated through three crews
of three during its operational time. Skylab’s experiments confirmed coronal holes and were able to photograph eight solar flares.
Mir
The International Space Station of today is a modern research facility
Russian station Mir,
from 1986 to 2001, was the first long term inhabited space station.
Occupied in low Earth orbit for twelve and a half years, Mir served a
permanent microgravity laboratory. Crews experimented with biology, human biology, physics, astronomy, meteorology and spacecraft systems. Goals included developing technologies for permanent occupation of space.
International Space Station
The International Space Station received its first crew as part of Expedition 1,
in November 2000, an internationally co-operative mission of almost 20
participants. The station has been continuously occupied for 18 years
and 202 days, exceeding the previous record, almost ten years by Russian
station Mir.
The ISS provides research in microgravity, and exposure to the local
space environment. Crew members conduct tests relevant to biology,
physics, astronomy, and others. Even studying the experience and health
of the crew advances space research.