Schwarzschild metric

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Schwarzschild_metric

In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild vacuum or Schwarzschild solution) is the solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. It was found by Karl Schwarzschild in 1916, and around the same time independently by Johannes Droste, who published his much more complete and modern-looking discussion only four months after Schwarzschild.

According to Birkhoff's theorem, the Schwarzschild metric is the most general spherically symmetric vacuum solution of the Einstein field equations. A Schwarzschild black hole or static black hole is a black hole that has neither electric charge nor angular momentum. A Schwarzschild black hole is described by the Schwarzschild metric, and cannot be distinguished from any other Schwarzschild black hole except by its mass.

The Schwarzschild black hole is characterized by a surrounding spherical boundary, called the event horizon, which is situated at the Schwarzschild radius, often called the radius of a black hole. The boundary is not a physical surface, and if a person fell through the event horizon (before being torn apart by tidal forces), they would not notice any physical surface at that position; it is a mathematical surface which is significant in determining the black hole's properties. Any non-rotating and non-charged mass that is smaller than its Schwarzschild radius forms a black hole. The solution of the Einstein field equations is valid for any mass M, so in principle (according to general relativity theory) a Schwarzschild black hole of any mass could exist if conditions became sufficiently favorable to allow for its formation.

The Schwarzschild metric

The Schwarzschild metric is a spherically symmetric Lorentzian metric (here, with signature convention (-, +, +, +),) defined on (a subset of)

${\displaystyle \mathbb {R} \times \left(E^{3}-O\right)\cong \mathbb {R} \times (0,\infty )\times S^{2}}$

where ${\displaystyle E^{3}}$ is 3 dimensional Euclidean space, and ${\displaystyle S^{2}\subset E^{3}}$ is the two sphere. The rotation group ${\displaystyle SO(3)=SO(E^{3})}$ acts on the ${\displaystyle E^{3}-O}$ or ${\displaystyle S^{2}}$ factor as rotations around the center ${\displaystyle O}$, while leaving the first ${\displaystyle \mathbb {R} }$ factor unchanged. The Schwarzschild metric is a solution of Einstein's field equations in empty space, meaning that it is valid only outside the gravitating body. That is, for a spherical body of radius ${\displaystyle R}$ the solution is valid for ${\displaystyle r>R}$. To describe the gravitational field both inside and outside the gravitating body the Schwarzschild solution must be matched with some suitable interior solution at ${\displaystyle r=R}$, such as the interior Schwarzschild metric.

In Schwarzschild coordinates ${\displaystyle (t,r,\theta ,\phi )}$ the Schwarzschild metric (or equivalently, the line element for proper time) has the form

${\displaystyle g=-c^{2}\,{d\tau }^{2}=-\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)c^{2}\,dt^{2}+\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)^{-1}\,dr^{2}+r^{2}g_{\Omega },}$

where ${\displaystyle g_{\Omega }}$ is the metric on the two sphere, i.e. ${\displaystyle g_{\Omega }=\left(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}\right)}$. Furthermore,

• ${\displaystyle d\tau ^{2}}$ is positive for time like curves, and ${\displaystyle \tau }$ is the proper time (time measured by a clock moving along the same world line with the test particle),
• ${\displaystyle c}$ is the speed of light,
• ${\displaystyle t}$ is the time coordinate (measured by a stationary clock located infinitely far from the massive body),
• ${\displaystyle r}$ is the radial coordinate (measured as the circumference, divided by 2π, of a sphere centered around the massive body),
• ${\displaystyle \Omega }$ is a point on the two sphere ${\displaystyle S^{2}}$,
• ${\displaystyle \theta }$ is the colatitude of ${\displaystyle \Omega }$ (angle from north, in units of radians) defined after arbitrarily choosing a z-axis,
• ${\displaystyle \phi }$ is the longitude of ${\displaystyle \Omega }$ (also in radians) around the chosen z-axis, and
• ${\displaystyle r_{s}}$ is the Schwarzschild radius of the massive body, a scale factor which is related to its mass ${\displaystyle M}$ by ${\displaystyle r_{s}={\frac {2GM}{c^{2}}}}$, where ${\displaystyle G}$ is the gravitational constant.

The Schwarzschild metric has a singularity for ${\displaystyle r=0}$ which is an intrinsic curvature singularity. It also seems to have a singularity on the event horizon ${\displaystyle r=r_{s}}$. Depending on the point of view, the metric is therefore defined only on the exterior region ${\displaystyle r>r_{s}}$, only on the interior region ${\displaystyle r$ or their disjoint union. However, the metric is actually non singular across the event horizon as one sees in suitable coordinates (see below). For ${\displaystyle r\gg r_{s}}$, the Schwarzschild metric is asymptotic to the standard Lorentz metric on Minkowski space. For almost all astrophysical objects, the ratio ${\displaystyle {\frac {r_{s}}{r}}}$ is extremely small. For example, the Schwarzschild radius ${\displaystyle r_{s}^{(\mathrm {Earth} )}}$ of the Earth is roughly 8.9 mm, while the Sun, which is 3.3×10⁵ times as massive has a Schwarzschild radius ${\displaystyle r_{s}^{(\mathrm {Sun} )}}$ of approximately 3.0 km. The ratio becomes large only in close proximity to black holes and other ultra-dense objects such as neutron stars.

The radial coordinate turns out to have physical significance as the "proper distance between two events that occur simultaneously relative to the radially moving geodesic clocks, the two events lying on the same radial coordinate line".

The Schwarzschild solution is analogous to a classical Newtonian theory of gravity that corresponds to the gravitational field around a point particle. Even at the surface of the Earth, the corrections to Newtonian gravity are only one part in a billion.

History

The Schwarzschild solution is named in honour of Karl Schwarzschild, who found the exact solution in 1915 and published it in January 1916, a little more than a month after the publication of Einstein's theory of general relativity. It was the first exact solution of the Einstein field equations other than the trivial flat space solution. Schwarzschild died shortly after his paper was published, as a result of a disease he contracted while serving in the German army during World War I.

Johannes Droste in 1916 independently produced the same solution as Schwarzschild, using a simpler, more direct derivation.

In the early years of general relativity there was a lot of confusion about the nature of the singularities found in the Schwarzschild and other solutions of the Einstein field equations. In Schwarzschild's original paper, he put what we now call the event horizon at the origin of his coordinate system. In this paper he also introduced what is now known as the Schwarzschild radial coordinate (r in the equations above), as an auxiliary variable. In his equations, Schwarzschild was using a different radial coordinate that was zero at the Schwarzschild radius. 

A more complete analysis of the singularity structure was given by David Hilbert in the following year, identifying the singularities both at r = 0 and r = r_s. Although there was general consensus that the singularity at r = 0 was a 'genuine' physical singularity, the nature of the singularity at r = r_s remained unclear.

In 1921 Paul Painlevé and in 1922 Allvar Gullstrand independently produced a metric, a spherically symmetric solution of Einstein's equations, which we now know is coordinate transformation of the Schwarzschild metric, Gullstrand–Painlevé coordinates, in which there was no singularity at r = r_s. They, however, did not recognize that their solutions were just coordinate transforms, and in fact used their solution to argue that Einstein's theory was wrong. In 1924 Arthur Eddington produced the first coordinate transformation (Eddington–Finkelstein coordinates) that showed that the singularity at r = r_s was a coordinate artifact, although he also seems to have been unaware of the significance of this discovery. Later, in 1932, Georges Lemaître gave a different coordinate transformation (Lemaître coordinates) to the same effect and was the first to recognize that this implied that the singularity at r = r_s was not physical. In 1939 Howard Robertson showed that a free falling observer descending in the Schwarzschild metric would cross the r = r_s singularity in a finite amount of proper time even though this would take an infinite amount of time in terms of coordinate time t.

In 1950, John Synge produced a paper that showed the maximal analytic extension of the Schwarzschild metric, again showing that the singularity at r = r_s was a coordinate artifact and that it represented two horizons. A similar result was later rediscovered by George Szekeres, and independently Martin Kruskal. The new coordinates nowadays known as Kruskal-Szekeres coordinates were much simpler than Synge's but both provided a single set of coordinates that covered the entire spacetime. However, perhaps due to the obscurity of the journals in which the papers of Lemaître and Synge were published their conclusions went unnoticed, with many of the major players in the field including Einstein believing that singularity at the Schwarzschild radius was physical.

Real progress was made in the 1960s when the more exact tools of differential geometry entered the field of general relativity, allowing more exact definitions of what it means for a Lorentzian manifold to be singular. This led to definitive identification of the r = r_s singularity in the Schwarzschild metric as an event horizon (a hypersurface in spacetime that can be crossed in only one direction).

Singularities and black holes

The Schwarzschild solution appears to have singularities at r = 0 and r = r_s; some of the metric components "blow up" (entail division by zero or division by infinity) at these radii. Since the Schwarzschild metric is expected to be valid only for those radii larger than the radius R of the gravitating body, there is no problem as long as R > r_s. For ordinary stars and planets this is always the case. For example, the radius of the Sun is approximately 700000 km, while its Schwarzschild radius is only 3 km.

The singularity at r = r_s divides the Schwarzschild coordinates in two disconnected patches. The exterior Schwarzschild solution with r > r_s is the one that is related to the gravitational fields of stars and planets. The interior Schwarzschild solution with 0 ≤ r < r_s, which contains the singularity at r = 0, is completely separated from the outer patch by the singularity at r = r_s. The Schwarzschild coordinates therefore give no physical connection between the two patches, which may be viewed as separate solutions. The singularity at r = r_s is an illusion however; it is an instance of what is called a coordinate singularity. As the name implies, the singularity arises from a bad choice of coordinates or coordinate conditions. When changing to a different coordinate system (for example Lemaitre coordinates, Eddington–Finkelstein coordinates, Kruskal–Szekeres coordinates, Novikov coordinates, or Gullstrand–Painlevé coordinates) the metric becomes regular at r = r_s and can extend the external patch to values of r smaller than r_s. Using a different coordinate transformation one can then relate the extended external patch to the inner patch.

The case r = 0 is different, however. If one asks that the solution be valid for all r one runs into a true physical singularity, or gravitational singularity, at the origin. To see that this is a true singularity one must look at quantities that are independent of the choice of coordinates. One such important quantity is the Kretschmann invariant, which is given by

${\displaystyle R^{\alpha \beta \gamma \delta }R_{\alpha \beta \gamma \delta }={\frac {12r_{\mathrm {s} }^{2}}{r^{6}}}={\frac {48G^{2}M^{2}}{c^{4}r^{6}}}\,.}$

At r = 0 the curvature becomes infinite, indicating the presence of a singularity. At this point the metric, and spacetime itself, is no longer well-defined. For a long time it was thought that such a solution was non-physical. However, a greater understanding of general relativity led to the realization that such singularities were a generic feature of the theory and not just an exotic special case. 

The Schwarzschild solution, taken to be valid for all r > 0, is called a Schwarzschild black hole. It is a perfectly valid solution of the Einstein field equations, although it has some rather bizarre properties. For r < r_s the Schwarzschild radial coordinate r becomes timelike and the time coordinate t becomes spacelike. A curve at constant r is no longer a possible worldline of a particle or observer, not even if a force is exerted to try to keep it there; this occurs because spacetime has been curved so much that the direction of cause and effect (the particle's future light cone) points into the singularity. The surface r = r_s demarcates what is called the event horizon of the black hole. It represents the point past which light can no longer escape the gravitational field. Any physical object whose radius R becomes less than or equal to the Schwarzschild radius will undergo gravitational collapse and become a black hole.

Alternative coordinates

The Schwarzschild solution can be expressed in a range of different choices of coordinates besides the Schwarzschild coordinates used above. Different choices tend to highlight different features of the solution.

Flamm's paraboloid

A plot of Flamm's paraboloid. It should not be confused with the unrelated concept of a gravity well.

 

The spatial curvature of the Schwarzschild solution for r > r_s can be visualized as the graphic shows. Consider a constant time equatorial slice through the Schwarzschild solution (θ = ​^π⁄₂, t = constant) and let the position of a particle moving in this plane be described with the remaining Schwarzschild coordinates (r, φ). Imagine now that there is an additional Euclidean dimension w, which has no physical reality (it is not part of spacetime). Then replace the (r, φ) plane with a surface dimpled in the w direction according to the equation (Flamm's paraboloid)

${\displaystyle w=2{\sqrt {r_{\mathrm {s} }\left(r-r_{\mathrm {s} }\right)}}.}$

This surface has the property that distances measured within it match distances in the Schwarzschild metric, because with the definition of w above,

${\displaystyle dw^{2}+dr^{2}+r^{2}\,d\varphi ^{2}=-c^{2}\,d\tau ^{2}={\frac {dr^{2}}{1-{\frac {r_{\mathrm {s} }}{r}}}}+r^{2}\,d\varphi ^{2}}$

Thus, Flamm's paraboloid is useful for visualizing the spatial curvature of the Schwarzschild metric. It should not, however, be confused with a gravity well. No ordinary (massive or massless) particle can have a worldline lying on the paraboloid, since all distances on it are spacelike (this is a cross-section at one moment of time, so any particle moving on it would have an infinite velocity). Even a tachyon would not move along the path that one might naively expect from a "rubber sheet" analogy: in particular, if the dimple is drawn pointing upward rather than downward, the tachyon's path still curves toward the central mass, not away. See the gravity well article for more information. 

Flamm's paraboloid may be derived as follows. The Euclidean metric in the cylindrical coordinates (r, φ, w) is written

${\displaystyle ds^{2}=dw^{2}+dr^{2}+r^{2}\,d\varphi ^{2}\,.}$

Letting the surface be described by the function w = w(r), the Euclidean metric can be written as

${\displaystyle ds^{2}=\left(1+\left({\frac {dw}{dr}}\right)^{2}\right)\,dr^{2}+r^{2}\,d\varphi ^{2}\,,}$

Comparing this with the Schwarzschild metric in the equatorial plane (θ = π/2) at a fixed time (t = constant, dt = 0)

${\displaystyle ds^{2}=\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)^{-1}\,dr^{2}+r^{2}\,d\varphi ^{2}\,,}$

yields an integral expression for w(r):

${\displaystyle w(r)=\int {\frac {dr}{\sqrt {{\frac {r}{r_{\mathrm {s} }}}-1}}}=2r_{\mathrm {s} }{\sqrt {{\frac {r}{r_{\mathrm {s} }}}-1}}+{\mbox{constant}}}$

whose solution is Flamm's paraboloid.

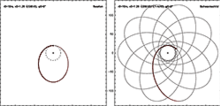
Orbital motion

Comparison between the orbit of a test particle in Newtonian (left) and Schwarzschild (right) spacetime; note the Apsidal precession on the right.

A particle orbiting in the Schwarzschild metric can have a stable circular orbit with r > 3r_s. Circular orbits with r between 1.5r_s and 3r_s are unstable, and no circular orbits exist for r < 1.5r_s. The circular orbit of minimum radius 1.5r_s corresponds to an orbital velocity approaching the speed of light. It is possible for a particle to have a constant value of r between r_s and 1.5r_s, but only if some force acts to keep it there.

Noncircular orbits, such as Mercury's, dwell longer at small radii than would be expected classically. This can be seen as a less extreme version of the more dramatic case in which a particle passes through the event horizon and dwells inside it forever. Intermediate between the case of Mercury and the case of an object falling past the event horizon, there are exotic possibilities such as knife-edge orbits, in which the satellite can be made to execute an arbitrarily large number of nearly circular orbits, after which it flies back outward.

Symmetries

The group of isometries of the Schwarzschild metric is the subgroup of the ten-dimensional Poincaré group which takes the time axis (trajectory of the star) to itself. It omits the spatial translations (three dimensions) and boosts (three dimensions). It retains the time translations (one dimension) and rotations (three dimensions). Thus it has four dimensions. Like the Poincaré group, it has four connected components: the component of the identity; the time reversed component; the spatial inversion component; and the component which is both time reversed and spatially inverted.

Curvatures

The Ricci curvature scalar and the Ricci curvature tensor are both zero. Non-zero components of the Riemann curvature tensor are

${\displaystyle R^{t}{}_{rrt}=2R^{\theta }{}_{r\theta r}=2R^{\phi }{}_{r\phi r}={\frac {r_{s}}{r^{2}(r_{s}-r)}},}$

${\displaystyle 2R^{t}{}_{\theta \theta t}=2R^{r}{}_{\theta \theta r}=R^{\phi }{}_{\theta \phi \theta }={\frac {r_{s}}{r}},}$

${\displaystyle 2R^{t}{}_{\phi \phi t}=2R^{r}{}_{\phi \phi r}=-R^{\theta }{}_{\phi \phi \theta }={\frac {r_{s}\sin ^{2}(\theta )}{r}},}$

${\displaystyle R^{r}{}_{trt}=-2R^{\theta }{}_{t\theta t}=-2R^{\phi }{}_{t\phi t}=c^{2}{\frac {r_{s}(r_{s}-r)}{r^{4}}}}$

Components which are obtainable by the symmetries of the Riemann tensor are not displayed.

To understand the physical meaning of these quantities, it is useful to express the curvature tensor in an orthonormal basis. In an orthonormal basis of an observer the non-zero components in geometric units are

${\displaystyle R^{\hat {r}}{}_{{\hat {t}}{\hat {r}}{\hat {t}}}=-R^{\hat {\theta }}{}_{{\hat {\phi }}{\hat {\theta }}{\hat {\phi }}}=-{\frac {r_{s}}{r^{3}}},}$

${\displaystyle R^{\hat {\theta }}{}_{{\hat {t}}{\hat {\theta }}{\hat {t}}}=R^{\hat {\phi }}{}_{{\hat {t}}{\hat {\phi }}{\hat {t}}}=-R^{\hat {r}}{}_{{\hat {\theta }}{\hat {r}}{\hat {\theta }}}=-R^{\hat {r}}{}_{{\hat {\phi }}{\hat {r}}{\hat {\phi }}}={\frac {r_{s}}{2r^{3}}}.}$

Again, components which are obtainable by the symmetries of the Riemann tensor are not displayed. These results are invariant to any Lorentz boost, thus the components do not change for non-static observers. The geodesic deviation equation shows that the tidal acceleration between two observers separated by ${\displaystyle \xi ^{\hat {j}}}$ is ${\displaystyle D^{2}\xi ^{\hat {j}}/D\tau ^{2}=-R^{\hat {j}}{}_{{\hat {t}}{\hat {k}}{\hat {t}}}\xi ^{\hat {k}}}$, so a body of length ${\displaystyle L}$ is stretched in the radial direction by an apparent acceleration ${\displaystyle (r_{s}/r^{3})c^{2}L}$ and squeezed in the perpendicular directions by ${\displaystyle -(r_{s}/(2r^{3}))c^{2}L}$.

Quran desecration

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Quran_desecration

The term "Quran desecration" is defined as insulting the Quran—which Muslims believe to be the literal word of God, in its original Arabic form—by defiling or defacing copies. Intentionally insulting the Quran is regarded by Muslims as blasphemous.

Most traditional schools of Islamic law require wudu (ritual handwashing) before a Muslim may touch the Quran. Muslims must always treat the printed book with reverence, which may even extend to excerpts of text.

Disposal of worn copies is also of concern to Muslims. Because the Quran contains no specifics on how to dispose of a worn or defective text, different and conflicting methods of disposal have been adopted in different regions by different sects. According to Islamic historian Michael Cook the Quran should be wrapped in cloth and buried on holy ground where it is unlikely to be trampled on or "safely" placed where it is unlikely to come into contact with impurity. According to Arab News, Muslims are forbidden to recycle, pulp, or shred worn-out copies of the text; instead, burning or burying the worn-out copies in a respectful manner is required.

Respect for the written text of the Quran is an important element of religious faith in Islam. Intentionally desecrating a copy of the Quran is punishable by imprisonment in some countries (up to life imprisonment in Pakistan, according to Article 295-B of the Penal Code) and could lead to death in Afghanistan, Saudi Arabia, Somalia and Pakistan.

Notable instances

2005 - Guantanamo

In mid-2005, allegations of deliberate desecration of the Quran in front of Muslim prisoners at the United States military Guantanamo Bay detention camp, Cuba fueled widespread controversy and led to ensuing Muslim riots. A US military investigation confirmed four instances of Quran desecration by US personnel (two of which were described as "unintentional"), and fifteen instances of desecration by Muslim prisoners. According to CBC News, "The statement did not provide any explanation about why the detainees might have abused their own Holy books." In May 2005, a report in Newsweek, claiming that it was U.S. interrogators who desecrated the Quran at the Guantanamo Bay base, further sparking Muslim unrest.

2007 - Nigeria

In 2007, Nigerian Christian teacher Christianah Oluwatoyin Oluwasesin was stabbed to death after allegations that she had desecrated a Quran.

2010/2011 - United States

In 2010, Christian pastor Terry Jones of the Dove World Outreach Center, a church in Gainesville, Florida, provoked international condemnation after announcing plans to burn a Quran on the anniversary of the Islamic terrorist September 11 attacks on the United States. He later cancelled the plans; however, on March 20, 2011, he oversaw the burning of a Quran. In response, Muslims in Afghanistan rioted and 12 people were killed.

In the 2011 Louis Theroux documentary America's Most Hated Family in Crisis, Megan Phelps of the Westboro Baptist Church explained in an interview that they deliberately and publicly burned a copy of the Quran.

2012 - Bangladesh

On September 29, an Islamic mob estimated at 25,000 vandalized and torched Buddhist temples, shrines, and houses, along with Hindu temples as incited by an alleged Facebook Buddhist posting of an image depicting the desecration of a Quran. The violence started in Ramu Upazila in Cox's Bazar District and later spread to other areas of Bangladesh.

2012/2015 - Afghanistan

In February 2012, protests broke out in various parts of Afghanistan over the improper disposal of Qurans at the US military Bagram Air Base. Protesters shouted "Death to America" and burned US flags. At least 30 people were killed and hundreds injured. Also,6 U.S. soldiers were killed after members of the Afghan National Security Forces turned their weapons on them and the Afghan protesters.

On March 19, 2015, Farkhunda Malikzada, a 27-year-old Afghan woman, was publicly beaten and slain by a mob of hundreds of people in Kabul. Farkhunda had previously been arguing with a mullah named Zainuddin, in front of a mosque where she worked as a religious teacher, about his practice of selling charms at the Shah-Do Shamshira Mosque, the Shrine of the King of Two Swords, a religious shrine in Kabul. During this argument, Zainuddin reportedly falsely accused her of burning the Quran. Police investigations revealed that she had not burned anything. A number of prominent public officials turned to Facebook immediately after the death to endorse the murder. After it was revealed that she did not burn the Quran, the public reaction in Afghanistan turned to shock and anger. Her murder led to 49 arrests; three adult men received twenty-year prison sentences, eight other adult males received sixteen year sentences, a minor received a ten-year sentence, and eleven police officers received one-year prison terms for failing to protect Farkhunda. Her murder and the subsequent protests served to draw attention to women's rights in Afghanistan.

Others

Saudi Arabia destroys Qurans of pilgrims that fall short of state standards. The preferred method is by burning, to avoid soiling the pages.

In March 2013, the al Qaeda English-language magazine Inspire published a poster stating "Wanted dead or alive for crimes against Islam" with a prominent image of Terry Jones, known for public Quran burning events. Iran's news agency, IRIB, reported on April 8, 2013, that Terry Jones planned another Quran burning event on September 11, 2013. On April 11, IRIB published statements from an Iranian MP who said the West must stop the event and warned that "the blasphemous move will spark an uncontrollable wave of outrage among over 1.6 billion people across the globe who follow Islam." In Pakistan, protesters set the American flag and effigy of the US pastor Terry Jones on fire, condemning the 9/11 plan, according to an April 14, 2013 article in The Nation.

In October 2013, a Turkish woman was arrested on suspicion of blasphemy and inciting religious hatred after allegedly stepping on Quran and then posting the picture on Twitter.

Proposals to recycle old Qurans in Pakistan have met with opposition.

On July 31, 2016, a couple of days after the Normandy church attack, several copies of the Quran at the multi-faith room of Mater Dei Hospital in Malta were desecrated when slices of pork were laid inside the book. The perpetrators also left a photo of Jacques Hamel, the Catholic priest murdered during the attack, with the caption "Victim of Islam".