Rocket

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Rocket 

The Soyuz TMA-9 spacecraft launches from the Baikonur Cosmodrome, Site 1/5 in Kazakhstan

A rocket (from Italian: rocchetto, lit. 'bobbin/spool') is a spacecraft, aircraft, vehicle or projectile that obtains thrust from a rocket engine. Rocket engine exhaust is formed entirely from propellant carried within the rocket. Rocket engines work by action and reaction and push rockets forward simply by expelling their exhaust in the opposite direction at high speed, and can therefore work in the vacuum of space.

In fact, rockets work more efficiently in the vacuum of space than in an atmosphere. Multistage rockets are capable of attaining escape velocity from Earth and therefore can achieve unlimited maximum altitude. Compared with airbreathing engines, rockets are lightweight and powerful and capable of generating large accelerations. To control their flight, rockets rely on momentum, airfoils, auxiliary reaction engines, gimballed thrust, momentum wheels, deflection of the exhaust stream, propellant flow, spin, or gravity.

Rockets for military and recreational uses date back to at least 13th-century China. Significant scientific, interplanetary and industrial use did not occur until the 20th century, when rocketry was the enabling technology for the Space Age, including setting foot on the Earth's moon. Rockets are now used for fireworks, weaponry, ejection seats, launch vehicles for artificial satellites, human spaceflight, and space exploration.

Chemical rockets are the most common type of high power rocket, typically creating a high speed exhaust by the combustion of fuel with an oxidizer. The stored propellant can be a simple pressurized gas or a single liquid fuel that disassociates in the presence of a catalyst (monopropellant), two liquids that spontaneously react on contact (hypergolic propellants), two liquids that must be ignited to react (like kerosene (RP1) and liquid oxygen, used in most liquid-propellant rockets), a solid combination of fuel with oxidizer (solid fuel), or solid fuel with liquid or gaseous oxidizer (hybrid propellant system). Chemical rockets store a large amount of energy in an easily released form, and can be very dangerous. However, careful design, testing, construction and use minimizes risks.

History

The oldest known depiction of rocket arrows, from the Huolongjing. The left arrow reads 'fire arrow' (huo jian), the middle is an 'dragon shaped arrow frame' (long xing jian jia), and the left is a 'complete fire arrow' (huo jian quan shi)

 

Main article: History of rockets

Further information: Timeline of rocket and missile technology

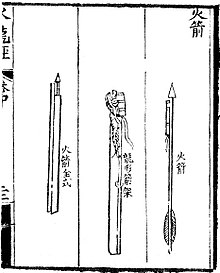
The first gunpowder-powered rockets evolved in medieval China under the Song dynasty by the 13th century. They also developed an early form of MLRS during this time. The Mongols adopted Chinese rocket technology and the invention spread via the Mongol invasions to the Middle East and to Europe in the mid-13th century. Rockets are recorded in use by the Song navy in a military exercise dated to 1245. Internal-combustion rocket propulsion is mentioned in a reference to 1264, recording that the "ground-rat", a type of firework, had frightened the Empress-Mother Gongsheng at a feast held in her honor by her son the Emperor Lizong. Subsequently, rockets are included in the military treatise Huolongjing, also known as the Fire Drake Manual, written by the Chinese artillery officer Jiao Yu in the mid-14th century. This text mentions the first known multistage rocket, the 'fire-dragon issuing from the water' (Huo long chu shui), thought to have been used by the Chinese navy.

Medieval and early modern rockets were used militarily as incendiary weapons in sieges. Between 1270 and 1280, Hasan al-Rammah wrote al-furusiyyah wa al-manasib al-harbiyya (The Book of Military Horsemanship and Ingenious War Devices), which included 107 gunpowder recipes, 22 of them for rockets. In Europe, Konrad Kyeser described rockets in his military treatise Bellifortis around 1405.

William Congreve at the bombardment of Copenhagen (1807)

The name "rocket" comes from the Italian rocchetta, meaning "bobbin" or "little spindle", given due to the similarity in shape to the bobbin or spool used to hold the thread from a spinning wheel. Leonhard Fronsperger and Conrad Haas adopted the Italian term into German in the mid-16th century; "rocket" appears in English by the early 17th century. Artis Magnae Artilleriae pars prima, an important early modern work on rocket artillery, by Casimir Siemienowicz, was first printed in Amsterdam in 1650.

An East India Company battalion was defeated during the Battle of Guntur, by the forces of Hyder Ali, who effectively utilized Mysorean rockets and rocket artillery against the closely massed East India Company forces.

The Mysorean rockets were the first successful iron-cased rockets, developed in the late 18th century in the Kingdom of Mysore (part of present-day India) under the rule of Hyder Ali. The Congreve rocket was a British weapon designed and developed by Sir William Congreve in 1804. This rocket was based directly on the Mysorean rockets, used compressed powder and was fielded in the Napoleonic Wars. It was Congreve rockets to which Francis Scott Key was referring, when he wrote of the "rockets’ red glare" while held captive on a British ship that was laying siege to Fort McHenry in 1814. Together, the Mysorean and British innovations increased the effective range of military rockets from 100 to 2,000 yards.

The first mathematical treatment of the dynamics of rocket propulsion is due to William Moore (1813). In 1814 William Congreve published a book in which he discussed the use of multiple rocket launching apparatus. In 1815 Alexander Dmitrievich Zasyadko constructed rocket-launching platforms, which allowed rockets to be fired in salvos (6 rockets at a time), and gun-laying devices. William Hale in 1844 greatly increased the accuracy of rocket artillery. Edward Mounier Boxer further improved the Congreve rocket in 1865.

William Leitch first proposed the concept of using rockets to enable human spaceflight in 1861. Konstantin Tsiolkovsky later (in 1903) also conceived this idea, and extensively developed a body of theory that has provided the foundation for subsequent spaceflight development.

The British Royal Flying Corps designed a guided rocket during World War I. Archibald Low stated “...in 1917 the Experimental Works designed an electrically steered rocket… Rocket experiments were conducted under my own patents with the help of Cdr. Brock” The patent “Improvements in Rockets” was raised in July 1918 but not published until February 1923 for security reasons. Firing and Guidance controls could be either wire or wireless. The propulsion and guidance rocket eflux emerged from the deflecting cowl at the nose.

In 1920, Professor Robert Goddard of Clark University published proposed improvements to rocket technology in A Method of Reaching Extreme Altitudes. In 1923, Hermann Oberth (1894–1989) published Die Rakete zu den Planetenräumen ("The Rocket into Planetary Space")

Goddard with a liquid oxygen-gasoline rocket (1926)

Modern rockets originated in 1926 when Goddard attached a supersonic (de Laval) nozzle to a high pressure combustion chamber. These nozzles turn the hot gas from the combustion chamber into a cooler, hypersonic, highly directed jet of gas, more than doubling the thrust and raising the engine efficiency from 2% to 64%. His use of liquid propellants instead of gunpowder greatly lowered the weight and increased the effectiveness of rockets. Their use in World War II artillery developed the technology further and opened up the possibility of human spaceflight after 1945.

In 1943 production of the V-2 rocket began in Germany. In parallel with the German guided-missile programme, rockets were also used on aircraft, either for assisting horizontal take-off (RATO), vertical take-off (Bachem Ba 349 "Natter") or for powering them (Me 163, see list of World War II guided missiles of Germany). The Allies' rocket programs were less technological, relying mostly on unguided missiles like the Soviet Katyusha rocket in the artillery role, and the American anti tank bazooka projectile. These used solid chemical propellants.

The Americans captured a large number of German rocket scientists, including Wernher von Braun, in 1945, and brought them to the United States as part of Operation Paperclip. After World War II scientists used rockets to study high-altitude conditions, by radio telemetry of temperature and pressure of the atmosphere, detection of cosmic rays, and further techniques; note too the Bell X-1, the first crewed vehicle to break the sound barrier (1947). Independently, in the Soviet Union's space program research continued under the leadership of the chief designer Sergei Korolev (1907–1966).

During the Cold War rockets became extremely important militarily with the development of modern intercontinental ballistic missiles (ICBMs). The 1960s saw rapid development of rocket technology, particularly in the Soviet Union (Vostok, Soyuz, Proton) and in the United States (e.g. the X-15). Rockets came into use for space exploration. American crewed programs (Project Mercury, Project Gemini and later the Apollo programme) culminated in 1969 with the first crewed landing on the Moon – using equipment launched by the Saturn V rocket.

Types

Vehicle configurations

Play media

Launch of Apollo 15 Saturn V rocket: T − 30 s through T + 40 s

Rocket vehicles are often constructed in the archetypal tall thin "rocket" shape that takes off vertically, but there are actually many different types of rockets including:

• tiny models such as balloon rockets, water rockets, skyrockets or small solid rockets that can be purchased at a hobby store
• missiles
• space rockets such as the enormous Saturn V used for the Apollo program
• rocket cars
• rocket bike
• rocket-powered aircraft (including rocket assisted takeoff of conventional aircraft – RATO)
• rocket sleds
• rocket trains
• rocket torpedoes
• rocket-powered jet packs
• rapid escape systems such as ejection seats and launch escape systems
• space probes

Design

A rocket design can be as simple as a cardboard tube filled with black powder, but to make an efficient, accurate rocket or missile involves overcoming a number of difficult problems. The main difficulties include cooling the combustion chamber, pumping the fuel (in the case of a liquid fuel), and controlling and correcting the direction of motion.

Components

Rockets consist of a propellant, a place to put propellant (such as a propellant tank), and a nozzle. They may also have one or more rocket engines, directional stabilization device(s) (such as fins, vernier engines or engine gimbals for thrust vectoring, gyroscopes) and a structure (typically monocoque) to hold these components together. Rockets intended for high speed atmospheric use also have an aerodynamic fairing such as a nose cone, which usually holds the payload.

As well as these components, rockets can have any number of other components, such as wings (rocketplanes), parachutes, wheels (rocket cars), even, in a sense, a person (rocket belt). Vehicles frequently possess navigation systems and guidance systems that typically use satellite navigation and inertial navigation systems.

Engines

Main article: Rocket engine

 

Viking 5C rocket engine

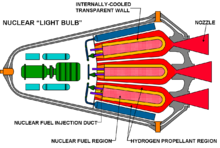
Rocket engines employ the principle of jet propulsion. The rocket engines powering rockets come in a great variety of different types; a comprehensive list can be found in the main article, Rocket engine. Most current rockets are chemically powered rockets (usually internal combustion engines, but some employ a decomposing monopropellant) that emit a hot exhaust gas. A rocket engine can use gas propellants, solid propellant, liquid propellant, or a hybrid mixture of both solid and liquid. Some rockets use heat or pressure that is supplied from a source other than the chemical reaction of propellant(s), such as steam rockets, solar thermal rockets, nuclear thermal rocket engines or simple pressurized rockets such as water rocket or cold gas thrusters. With combustive propellants a chemical reaction is initiated between the fuel and the oxidizer in the combustion chamber, and the resultant hot gases accelerate out of a rocket engine nozzle (or nozzles) at the rearward-facing end of the rocket. The acceleration of these gases through the engine exerts force ("thrust") on the combustion chamber and nozzle, propelling the vehicle (according to Newton's Third Law). This actually happens because the force (pressure times area) on the combustion chamber wall is unbalanced by the nozzle opening; this is not the case in any other direction. The shape of the nozzle also generates force by directing the exhaust gas along the axis of the rocket.

Propellant

Main article: Rocket propellant

Gas Core light bulb

Rocket propellant is mass that is stored, usually in some form of propellant tank or casing, prior to being used as the propulsive mass that is ejected from a rocket engine in the form of a fluid jet to produce thrust. For chemical rockets often the propellants are a fuel such as liquid hydrogen or kerosene burned with an oxidizer such as liquid oxygen or nitric acid to produce large volumes of very hot gas. The oxidiser is either kept separate and mixed in the combustion chamber, or comes premixed, as with solid rockets.

Sometimes the propellant is not burned but still undergoes a chemical reaction, and can be a 'monopropellant' such as hydrazine, nitrous oxide or hydrogen peroxide that can be catalytically decomposed to hot gas.

Alternatively, an inert propellant can be used that can be externally heated, such as in steam rocket, solar thermal rocket or nuclear thermal rockets.

For smaller, low performance rockets such as attitude control thrusters where high performance is less necessary, a pressurised fluid is used as propellant that simply escapes the spacecraft through a propelling nozzle.

Pendulum rocket fallacy

The first liquid-fuel rocket, constructed by Robert H. Goddard, differed significantly from modern rockets. The rocket engine was at the top and the fuel tank at the bottom of the rocket, based on Goddard's belief that the rocket would achieve stability by "hanging" from the engine like a pendulum in flight. However, the rocket veered off course and crashed 184 feet (56 m) away from the launch site, indicating that the rocket was no more stable than one with the rocket engine at the base.

Uses

Rockets or other similar reaction devices carrying their own propellant must be used when there is no other substance (land, water, or air) or force (gravity, magnetism, light) that a vehicle may usefully employ for propulsion, such as in space. In these circumstances, it is necessary to carry all the propellant to be used.

However, they are also useful in other situations:

Military

Main articles: Rocket artillery and Missile

A Trident II missile launched from sea.

Some military weapons use rockets to propel warheads to their targets. A rocket and its payload together are generally referred to as a missile when the weapon has a guidance system (not all missiles use rocket engines, some use other engines such as jets) or as a rocket if it is unguided. Anti-tank and anti-aircraft missiles use rocket engines to engage targets at high speed at a range of several miles, while intercontinental ballistic missiles can be used to deliver multiple nuclear warheads from thousands of miles, and anti-ballistic missiles try to stop them. Rockets have also been tested for reconnaissance, such as the Ping-Pong rocket, which was launched to surveil enemy targets, however, recon rockets have never come into wide use in the military.

Science and research

See also: Space probe

A Bumper sounding rocket

Sounding rockets are commonly used to carry instruments that take readings from 50 kilometers (31 mi) to 1,500 kilometers (930 mi) above the surface of the Earth. The first images of Earth from space were obtained from a V-2 rocket in 1946 (flight #13).

Rocket engines are also used to propel rocket sleds along a rail at extremely high speed. The world record for this is Mach 8.5.

Spaceflight

Main article: Spaceflight

Larger rockets are normally launched from a launch pad that provides stable support until a few seconds after ignition. Due to their high exhaust velocity—2,500 to 4,500 m/s (9,000 to 16,200 km/h; 5,600 to 10,100 mph)—rockets are particularly useful when very high speeds are required, such as orbital speed at approximately 7,800 m/s (28,000 km/h; 17,000 mph). Spacecraft delivered into orbital trajectories become artificial satellites, which are used for many commercial purposes. Indeed, rockets remain the only way to launch spacecraft into orbit and beyond. They are also used to rapidly accelerate spacecraft when they change orbits or de-orbit for landing. Also, a rocket may be used to soften a hard parachute landing immediately before touchdown (see retrorocket).

Rescue

Apollo LES pad abort test with boilerplate crew module.

Rockets were used to propel a line to a stricken ship so that a Breeches buoy can be used to rescue those on board. Rockets are also used to launch emergency flares.

Some crewed rockets, notably the Saturn V and Soyuz, have launch escape systems. This is a small, usually solid rocket that is capable of pulling the crewed capsule away from the main vehicle towards safety at a moments notice. These types of systems have been operated several times, both in testing and in flight, and operated correctly each time.

This was the case when the Safety Assurance System (Soviet nomenclature) successfully pulled away the L3 capsule during three of the four failed launches of the Soviet moon rocket, N1 vehicles 3L, 5L and 7L. In all three cases the capsule, albeit uncrewed, was saved from destruction. Only the three aforementioned N1 rockets had functional Safety Assurance Systems. The outstanding vehicle, 6L, had dummy upper stages and therefore no escape system giving the N1 booster a 100% success rate for egress from a failed launch.

A successful escape of a crewed capsule occurred when Soyuz T-10, on a mission to the Salyut 7 space station, exploded on the pad.

Solid rocket propelled ejection seats are used in many military aircraft to propel crew away to safety from a vehicle when flight control is lost.

Hobby, sport, and entertainment

Main article: model rocket

A model rocket is a small rocket designed to reach low altitudes (e.g., 100–500 m (330–1,640 ft) for 30 g (1.1 oz) model) and be recovered by a variety of means.

According to the United States National Association of Rocketry (nar) Safety Code, model rockets are constructed of paper, wood, plastic and other lightweight materials. The code also provides guidelines for motor use, launch site selection, launch methods, launcher placement, recovery system design and deployment and more. Since the early 1960s, a copy of the Model Rocket Safety Code has been provided with most model rocket kits and motors. Despite its inherent association with extremely flammable substances and objects with a pointed tip traveling at high speeds, model rocketry historically has proven to be a very safe hobby and has been credited as a significant source of inspiration for children who eventually become scientists and engineers.

Hobbyists build and fly a wide variety of model rockets. Many companies produce model rocket kits and parts but due to their inherent simplicity some hobbyists have been known to make rockets out of almost anything. Rockets are also used in some types of consumer and professional fireworks. A water rocket is a type of model rocket using water as its reaction mass. The pressure vessel (the engine of the rocket) is usually a used plastic soft drink bottle. The water is forced out by a pressurized gas, typically compressed air. It is an example of Newton's third law of motion.

The scale of amateur rocketry can range from a small rocket launched in one's own backyard to a rocket that reached space. Amateur rocketry is split into three categories according to total engine impulse: low-power, mid-power, and high-power.

Hydrogen peroxide rockets are used to power jet packs, and have been used to power cars and a rocket car holds the all time (albeit unofficial) drag racing record.

Corpulent Stump is the most powerful non-commercial rocket ever launched on an Aerotech engine in the United Kingdom.

Flight

Play media

Video of the launch of Space Shuttle Endeavour on STS-134

Launches for orbital spaceflights, or into interplanetary space, are usually from a fixed location on the ground, but would also be possible from an aircraft or ship.

Rocket launch technologies include the entire set of systems needed to successfully launch a vehicle, not just the vehicle itself, but also the firing control systems, mission control center, launch pad, ground stations, and tracking stations needed for a successful launch or recovery or both. These are often collectively referred to as the "ground segment".

Orbital launch vehicles commonly take off vertically, and then begin to progressively lean over, usually following a gravity turn trajectory.

Once above the majority of the atmosphere, the vehicle then angles the rocket jet, pointing it largely horizontally but somewhat downwards, which permits the vehicle to gain and then maintain altitude while increasing horizontal speed. As the speed grows, the vehicle will become more and more horizontal until at orbital speed, the engine will cut off.

All current vehicles stage, that is, jettison hardware on the way to orbit. Although vehicles have been proposed which would be able to reach orbit without staging, none have ever been constructed, and, if powered only by rockets, the exponentially increasing fuel requirements of such a vehicle would make its useful payload tiny or nonexistent. Most current and historical launch vehicles "expend" their jettisoned hardware, typically by allowing it to crash into the ocean, but some have recovered and reused jettisoned hardware, either by parachute or by propulsive landing.

Doglegged flight path of a PSLV launch to polar inclinations avoiding Sri Lankan landmass.

When launching a spacecraft to orbit, a "dogleg" is a guided, powered turn during ascent phase that causes a rocket's flight path to deviate from a "straight" path. A dogleg is necessary if the desired launch azimuth, to reach a desired orbital inclination, would take the ground track over land (or over a populated area, e.g. Russia usually does launch over land, but over unpopulated areas), or if the rocket is trying to reach an orbital plane that does not reach the latitude of the launch site. Doglegs are undesirable due to extra onboard fuel required, causing heavier load, and a reduction of vehicle performance.

Noise

Workers and media witness the Sound Suppression Water System test at Launch Pad 39A.

Rocket exhaust generates a significant amount of acoustic energy. As the supersonic exhaust collides with the ambient air, shock waves are formed. The sound intensity from these shock waves depends on the size of the rocket as well as the exhaust velocity. The sound intensity of large, high performance rockets could potentially kill at close range.

The Space Shuttle generated 180 dB of noise around its base. To combat this, NASA developed a sound suppression system which can flow water at rates up to 900,000 gallons per minute (57 m³/s) onto the launch pad. The water reduces the noise level from 180 dB down to 142 dB (the design requirement is 145 dB). Without the sound suppression system, acoustic waves would reflect off of the launch pad towards the rocket, vibrating the sensitive payload and crew. These acoustic waves can be so severe as to damage or destroy the rocket.

Noise is generally most intense when a rocket is close to the ground, since the noise from the engines radiates up away from the jet, as well as reflecting off the ground. This noise can be reduced somewhat by flame trenches with roofs, by water injection around the jet and by deflecting the jet at an angle.

For crewed rockets various methods are used to reduce the sound intensity for the passengers, and typically the placement of the astronauts far away from the rocket engines helps significantly. For the passengers and crew, when a vehicle goes supersonic the sound cuts off as the sound waves are no longer able to keep up with the vehicle.

Physics

Operation

Main article: Rocket engine

A balloon with a tapering nozzle. In this case, the nozzle itself does not push the balloon but is pulled by it. A convergent/divergent nozzle would be better.

The effect of the combustion of propellant in the rocket engine is to increase the internal energy of the resulting gases, utilizing the stored chemical energy in the fuel. As the internal energy increases, pressure increases, and a nozzle is utilized to convert this energy into a directed kinetic energy. This produces thrust against the ambient environment to which these gases are released. The ideal direction of motion of the exhaust is in the direction so as to cause thrust. At the top end of the combustion chamber the hot, energetic gas fluid cannot move forward, and so, it pushes upward against the top of the rocket engine's combustion chamber. As the combustion gases approach the exit of the combustion chamber, they increase in speed. The effect of the convergent part of the rocket engine nozzle on the high pressure fluid of combustion gases, is to cause the gases to accelerate to high speed. The higher the speed of the gases, the lower the pressure of the gas (Bernoulli's principle or conservation of energy) acting on that part of the combustion chamber. In a properly designed engine, the flow will reach Mach 1 at the throat of the nozzle. At which point the speed of the flow increases. Beyond the throat of the nozzle, a bell shaped expansion part of the engine allows the gases that are expanding to push against that part of the rocket engine. Thus, the bell part of the nozzle gives additional thrust. Simply expressed, for every action there is an equal and opposite reaction, according to Newton's third law with the result that the exiting gases produce the reaction of a force on the rocket causing it to accelerate the rocket.

Rocket thrust is caused by pressures acting on both the combustion chamber and nozzle

In a closed chamber, the pressures are equal in each direction and no acceleration occurs. If an opening is provided in the bottom of the chamber then the pressure is no longer acting on the missing section. This opening permits the exhaust to escape. The remaining pressures give a resultant thrust on the side opposite the opening, and these pressures are what push the rocket along.

The shape of the nozzle is important. Consider a balloon propelled by air coming out of a tapering nozzle. In such a case the combination of air pressure and viscous friction is such that the nozzle does not push the balloon but is pulled by it. Using a convergent/divergent nozzle gives more force since the exhaust also presses on it as it expands outwards, roughly doubling the total force. If propellant gas is continuously added to the chamber then these pressures can be maintained for as long as propellant remains. Note that in the case of liquid propellant engines, the pumps moving the propellant into the combustion chamber must maintain a pressure larger than the combustion chamber – typically on the order of 100 atmospheres.

As a side effect, these pressures on the rocket also act on the exhaust in the opposite direction and accelerate this exhaust to very high speeds (according to Newton's Third Law). From the principle of conservation of momentum the speed of the exhaust of a rocket determines how much momentum increase is created for a given amount of propellant. This is called the rocket's specific impulse. Because a rocket, propellant and exhaust in flight, without any external perturbations, may be considered as a closed system, the total momentum is always constant. Therefore, the faster the net speed of the exhaust in one direction, the greater the speed of the rocket can achieve in the opposite direction. This is especially true since the rocket body's mass is typically far lower than the final total exhaust mass.

Forces on a rocket in flight

Forces on a rocket in flight

The general study of the forces on a rocket is part of the field of ballistics. Spacecraft are further studied in the subfield of astrodynamics.

Flying rockets are primarily affected by the following:

• Thrust from the engine(s)
• Gravity from celestial bodies
• Drag if moving in atmosphere
• Lift; usually relatively small effect except for rocket-powered aircraft

In addition, the inertia and centrifugal pseudo-force can be significant due to the path of the rocket around the center of a celestial body; when high enough speeds in the right direction and altitude are achieved a stable orbit or escape velocity is obtained.

These forces, with a stabilizing tail (the empennage) present will, unless deliberate control efforts are made, naturally cause the vehicle to follow a roughly parabolic trajectory termed a gravity turn, and this trajectory is often used at least during the initial part of a launch. (This is true even if the rocket engine is mounted at the nose.) Vehicles can thus maintain low or even zero angle of attack, which minimizes transverse stress on the launch vehicle, permitting a weaker, and hence lighter, launch vehicle.

Drag

Main articles: Drag (physics), Gravity drag, and Aerodynamic drag

Drag is a force opposite to the direction of the rocket's motion relative to any air it is moving through. This slows the speed of the vehicle and produces structural loads. The deceleration forces for fast-moving rockets are calculated using the drag equation.

Drag can be minimised by an aerodynamic nose cone and by using a shape with a high ballistic coefficient (the "classic" rocket shape—long and thin), and by keeping the rocket's angle of attack as low as possible.

During a launch, as the vehicle speed increases, and the atmosphere thins, there is a point of maximum aerodynamic drag called max Q. This determines the minimum aerodynamic strength of the vehicle, as the rocket must avoid buckling under these forces.

Net thrust

For a more detailed model of the net thrust of a rocket engine that includes the effect of atmospheric pressure, see Rocket engine § Net thrust.

 

A rocket jet shape varies based on external air pressure. From top to bottom:

• Underexpanded
• Ideally expanded
• Overexpanded
• Grossly overexpanded

A typical rocket engine can handle a significant fraction of its own mass in propellant each second, with the propellant leaving the nozzle at several kilometres per second. This means that the thrust-to-weight ratio of a rocket engine, and often the entire vehicle can be very high, in extreme cases over 100. This compares with other jet propulsion engines that can exceed 5 for some of the better engines.

It can be shown that the net thrust of a rocket is:

${\displaystyle F_{n}={\dot {m}}\;v_{e}}$

where:

${\displaystyle {\dot {m}}=\,}$propellant flow (kg/s or lb/s)

${\displaystyle v_{e}=\,}$the effective exhaust velocity (m/s or ft/s)

The effective exhaust velocity ${\displaystyle v_{e}}$ is more or less the speed the exhaust leaves the vehicle, and in the vacuum of space, the effective exhaust velocity is often equal to the actual average exhaust speed along the thrust axis. However, the effective exhaust velocity allows for various losses, and notably, is reduced when operated within an atmosphere.

The rate of propellant flow through a rocket engine is often deliberately varied over a flight, to provide a way to control the thrust and thus the airspeed of the vehicle. This, for example, allows minimization of aerodynamic losses and can limit the increase of g-forces due to the reduction in propellant load.

Total impulse

Main article: Impulse (physics)

Impulse is defined as a force acting on an object over time, which in the absence of opposing forces (gravity and aerodynamic drag), changes the momentum (integral of mass and velocity) of the object. As such, it is the best performance class (payload mass and terminal velocity capability) indicator of a rocket, rather than takeoff thrust, mass, or "power". The total impulse of a rocket (stage) burning its propellant is:

${\displaystyle I=\int Fdt}$

When there is fixed thrust, this is simply:

${\displaystyle I=Ft\;}$

The total impulse of a multi-stage rocket is the sum of the impulses of the individual stages.

Specific impulse

Main article: specific impulse

I_sp in vacuum of various rockets

Rocket	Propellants	Isp, vacuum (s)
Space shuttle liquid engines	LOX/LH2	453
Space shuttle solid motors	APCP	268
Space shuttle OMS	NTO/MMH	313
Saturn V stage 1	LOX/RP-1	304

As can be seen from the thrust equation, the effective speed of the exhaust controls the amount of thrust produced from a particular quantity of fuel burnt per second.

An equivalent measure, the net impulse per weight unit of propellant expelled, is called specific Impulse, ${\displaystyle I_{sp}}$, and this is one of the most important figures that describes a rocket's performance. It is defined such that it is related to the effective exhaust velocity by:

${\displaystyle v_{e}=I_{sp}\cdot g_{0}}$

where:

${\displaystyle I_{sp}}$ has units of seconds

${\displaystyle g_{0}}$ is the acceleration at the surface of the Earth

Thus, the greater the specific impulse, the greater the net thrust and performance of the engine. ${\displaystyle I_{sp}}$ is determined by measurement while testing the engine. In practice the effective exhaust velocities of rockets varies but can be extremely high, ~4500 m/s, about 15 times the sea level speed of sound in air.

Delta-v (rocket equation)

Main article: Tsiolkovsky rocket equation

 

A map of approximate Delta-v's around the solar system between Earth and Mars

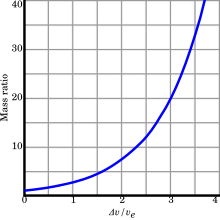
The delta-v capacity of a rocket is the theoretical total change in velocity that a rocket can achieve without any external interference (without air drag or gravity or other forces).

When ${\displaystyle v_{e}}$ is constant, the delta-v that a rocket vehicle can provide can be calculated from the Tsiolkovsky rocket equation:

${\displaystyle \Delta v\ =v_{e}\ln {\frac {m_{0}}{m_{1}}}}$}

where:

${\displaystyle m_{0}}$ is the initial total mass, including propellant, in kg (or lb)

${\displaystyle m_{1}}$ is the final total mass in kg (or lb)

${\displaystyle v_{e}}$ is the effective exhaust velocity in m/s (or ft/s)

${\displaystyle \Delta v\ }$ is the delta-v in m/s (or ft/s)

When launched from the Earth practical delta-vs for a single rockets carrying payloads can be a few km/s. Some theoretical designs have rockets with delta-vs over 9 km/s.

The required delta-v can also be calculated for a particular manoeuvre; for example the delta-v to launch from the surface of the Earth to Low earth orbit is about 9.7 km/s, which leaves the vehicle with a sideways speed of about 7.8 km/s at an altitude of around 200 km. In this manoeuvre about 1.9 km/s is lost in air drag, gravity drag and gaining altitude.

The ratio ${\displaystyle {\frac {m_{0}}{m_{1}}}}$ is sometimes called the mass ratio.

Mass ratios

Main article: Mass ratio

The Tsiolkovsky rocket equation gives a relationship between the mass ratio and the final velocity in multiples of the exhaust speed

Almost all of a launch vehicle's mass consists of propellant. Mass ratio is, for any 'burn', the ratio between the rocket's initial mass and its final mass. Everything else being equal, a high mass ratio is desirable for good performance, since it indicates that the rocket is lightweight and hence performs better, for essentially the same reasons that low weight is desirable in sports cars.

Rockets as a group have the highest thrust-to-weight ratio of any type of engine; and this helps vehicles achieve high mass ratios, which improves the performance of flights. The higher the ratio, the less engine mass is needed to be carried. This permits the carrying of even more propellant, enormously improving the delta-v. Alternatively, some rockets such as for rescue scenarios or racing carry relatively little propellant and payload and thus need only a lightweight structure and instead achieve high accelerations. For example, the Soyuz escape system can produce 20 g.

Achievable mass ratios are highly dependent on many factors such as propellant type, the design of engine the vehicle uses, structural safety margins and construction techniques.

The highest mass ratios are generally achieved with liquid rockets, and these types are usually used for orbital launch vehicles, a situation which calls for a high delta-v. Liquid propellants generally have densities similar to water (with the notable exceptions of liquid hydrogen and liquid methane), and these types are able to use lightweight, low pressure tanks and typically run high-performance turbopumps to force the propellant into the combustion chamber.

Some notable mass fractions are found in the following table (some aircraft are included for comparison purposes):

Vehicle	Takeoff mass	Final mass	Mass ratio	Mass fraction
Ariane 5 (vehicle + payload)	746,000 kg  (~1,645,000 lb)	2,700 kg + 16,000 kg (~6,000 lb + ~35,300 lb)	39.9	0.975
Titan 23G first stage	117,020 kg (258,000 lb)	4,760 kg (10,500 lb)	24.6	0.959
Saturn V	3,038,500 kg (~6,700,000 lb)	13,300 kg + 118,000 kg (~29,320 lb + ~260,150 lb)	23.1	0.957
Space Shuttle (vehicle + payload)	2,040,000 kg (~4,500,000 lb)	104,000 kg + 28,800 kg (~230,000 lb + ~63,500 lb)	15.4	0.935
Saturn 1B (stage only)	448,648 kg (989,100 lb)	41,594 kg (91,700 lb)	10.7	0.907
Virgin Atlantic GlobalFlyer	10,024.39 kg (22,100 lb)	1,678.3 kg (3,700 lb)	6.0	0.83
V-2	13,000 kg (~28,660 lb) (12.8 ton)		3.85	0.74
X-15	15,420 kg (34,000 lb)	6,620 kg (14,600 lb)	2.3	0.57
Concorde	~181,000 kg (400,000 lb )		2	0.5
Boeing 747	~363,000 kg (800,000 lb)		2	0.5

Staging

Main article: Multistage rocket

 

Spacecraft staging involves dropping off unnecessary parts of the rocket to reduce mass.

 

Apollo 6 while dropping the interstage ring

Thus far, the required velocity (delta-v) to achieve orbit has been unattained by any single rocket because the propellant, tankage, structure, guidance, valves and engines and so on, take a particular minimum percentage of take-off mass that is too great for the propellant it carries to achieve that delta-v carrying reasonable payloads. Since Single-stage-to-orbit has so far not been achievable, orbital rockets always have more than one stage.

For example, the first stage of the Saturn V, carrying the weight of the upper stages, was able to achieve a mass ratio of about 10, and achieved a specific impulse of 263 seconds. This gives a delta-v of around 5.9 km/s whereas around 9.4 km/s delta-v is needed to achieve orbit with all losses allowed for.

This problem is frequently solved by staging—the rocket sheds excess weight (usually empty tankage and associated engines) during launch. Staging is either serial where the rockets light after the previous stage has fallen away, or parallel, where rockets are burning together and then detach when they burn out.

The maximum speeds that can be achieved with staging is theoretically limited only by the speed of light. However the payload that can be carried goes down geometrically with each extra stage needed, while the additional delta-v for each stage is simply additive.

Acceleration and thrust-to-weight ratio

Main article: thrust-to-weight ratio

From Newton's second law, the acceleration, ${\displaystyle a}$, of a vehicle is simply:

${\displaystyle a={\frac {F_{n}}{m}}}$

where m is the instantaneous mass of the vehicle and ${\displaystyle F_{n}}$ is the net force acting on the rocket (mostly thrust, but air drag and other forces can play a part).

As the remaining propellant decreases, rocket vehicles become lighter and their acceleration tends to increase until the propellant is exhausted. This means that much of the speed change occurs towards the end of the burn when the vehicle is much lighter. However, the thrust can be throttled to offset or vary this if needed. Discontinuities in acceleration also occur when stages burn out, often starting at a lower acceleration with each new stage firing.

Peak accelerations can be increased by designing the vehicle with a reduced mass, usually achieved by a reduction in the fuel load and tankage and associated structures, but obviously this reduces range, delta-v and burn time. Still, for some applications that rockets are used for, a high peak acceleration applied for just a short time is highly desirable.

The minimal mass of vehicle consists of a rocket engine with minimal fuel and structure to carry it. In that case the thrust-to-weight ratio of the rocket engine limits the maximum acceleration that can be designed. It turns out that rocket engines generally have truly excellent thrust to weight ratios (137 for the NK-33 engine; some solid rockets are over 1000), and nearly all really high-g vehicles employ or have employed rockets.

The high accelerations that rockets naturally possess means that rocket vehicles are often capable of vertical takeoff, and in some cases, with suitable guidance and control of the engines, also vertical landing. For these operations to be done it is necessary for a vehicle's engines to provide more than the local gravitational acceleration.

Energy

Energy efficiency

Main article: propulsive efficiency

 

Space Shuttle Atlantis during launch phase

The energy density of a typical rocket propellant is often around one-third that of conventional hydrocarbon fuels; the bulk of the mass is (often relatively inexpensive) oxidizer. Nevertheless, at take-off the rocket has a great deal of energy in the fuel and oxidizer stored within the vehicle. It is of course desirable that as much of the energy of the propellant end up as kinetic or potential energy of the body of the rocket as possible.

Energy from the fuel is lost in air drag and gravity drag and is used for the rocket to gain altitude and speed. However, much of the lost energy ends up in the exhaust.

In a chemical propulsion device, the engine efficiency is simply the ratio of the kinetic power of the exhaust gases and the power available from the chemical reaction:

${\displaystyle \eta _{c}={\frac {{\frac {1}{2}}{\dot {m}}v_{e}^{2}}{\eta _{combustion}P_{chem}}}}$

100% efficiency within the engine (engine efficiency ${\displaystyle \eta _{c}=100\%}$) would mean that all the heat energy of the combustion products is converted into kinetic energy of the jet. This is not possible, but the near-adiabatic high expansion ratio nozzles that can be used with rockets come surprisingly close: when the nozzle expands the gas, the gas is cooled and accelerated, and an energy efficiency of up to 70% can be achieved. Most of the rest is heat energy in the exhaust that is not recovered. The high efficiency is a consequence of the fact that rocket combustion can be performed at very high temperatures and the gas is finally released at much lower temperatures, and so giving good Carnot efficiency.

However, engine efficiency is not the whole story. In common with the other jet-based engines, but particularly in rockets due to their high and typically fixed exhaust speeds, rocket vehicles are extremely inefficient at low speeds irrespective of the engine efficiency. The problem is that at low speeds, the exhaust carries away a huge amount of kinetic energy rearward. This phenomenon is termed propulsive efficiency (${\displaystyle \eta _{p}}$).

However, as speeds rise, the resultant exhaust speed goes down, and the overall vehicle energetic efficiency rises, reaching a peak of around 100% of the engine efficiency when the vehicle is travelling exactly at the same speed that the exhaust is emitted. In this case the exhaust would ideally stop dead in space behind the moving vehicle, taking away zero energy, and from conservation of energy, all the energy would end up in the vehicle. The efficiency then drops off again at even higher speeds as the exhaust ends up traveling forwards – trailing behind the vehicle.

Plot of instantaneous propulsive efficiency (blue) and overall efficiency for a rocket accelerating from rest (red) as percentages of the engine efficiency

From these principles it can be shown that the propulsive efficiency ${\displaystyle \eta _{p}}$ for a rocket moving at speed ${\displaystyle u}$ with an exhaust velocity ${\displaystyle c}$ is:

${\displaystyle \eta _{p}={\frac {2{\frac {u}{c}}}{1+({\frac {u}{c}})^{2}}}}$

And the overall (instantaneous) energy efficiency ${\displaystyle \eta }$ is:

${\displaystyle \eta =\eta _{p}\eta _{c}}$

For example, from the equation, with an ${\displaystyle \eta _{c}}$ of 0.7, a rocket flying at Mach 0.85 (which most aircraft cruise at) with an exhaust velocity of Mach 10, would have a predicted overall energy efficiency of 5.9%, whereas a conventional, modern, air-breathing jet engine achieves closer to 35% efficiency. Thus a rocket would need about 6x more energy; and allowing for the specific energy of rocket propellant being around one third that of conventional air fuel, roughly 18x more mass of propellant would need to be carried for the same journey. This is why rockets are rarely if ever used for general aviation.

Since the energy ultimately comes from fuel, these considerations mean that rockets are mainly useful when a very high speed is required, such as ICBMs or orbital launch. For example, NASA's space shuttle fires its engines for around 8.5 minutes, consuming 1,000 tonnes of solid propellant (containing 16% aluminium) and an additional 2,000,000 litres of liquid propellant (106,261 kg of liquid hydrogen fuel) to lift the 100,000 kg vehicle (including the 25,000 kg payload) to an altitude of 111 km and an orbital velocity of 30,000 km/h. At this altitude and velocity, the vehicle has a kinetic energy of about 3 TJ and a potential energy of roughly 200 GJ. Given the initial energy of 20 TJ, the Space Shuttle is about 16% energy efficient at launching the orbiter.

Thus jet engines, with a better match between speed and jet exhaust speed (such as turbofans—in spite of their worse ${\displaystyle \eta _{c}}$)—dominate for subsonic and supersonic atmospheric use, while rockets work best at hypersonic speeds. On the other hand, rockets serve in many short-range relatively low speed military applications where their low-speed inefficiency is outweighed by their extremely high thrust and hence high accelerations.

Oberth effect

Main article: Oberth effect

One subtle feature of rockets relates to energy. A rocket stage, while carrying a given load, is capable of giving a particular delta-v. This delta-v means that the speed increases (or decreases) by a particular amount, independent of the initial speed. However, because kinetic energy is a square law on speed, this means that the faster the rocket is travelling before the burn the more orbital energy it gains or loses.

This fact is used in interplanetary travel. It means that the amount of delta-v to reach other planets, over and above that to reach escape velocity can be much less if the delta-v is applied when the rocket is travelling at high speeds, close to the Earth or other planetary surface; whereas waiting until the rocket has slowed at altitude multiplies up the effort required to achieve the desired trajectory.

Safety, reliability and accidents

See also: List of spaceflight-related accidents and incidents

Space Shuttle Challenger torn apart T+73 seconds after hot gases escaped the SRBs, causing the breakup of the Shuttle stack

The reliability of rockets, as for all physical systems, is dependent on the quality of engineering design and construction.

Because of the enormous chemical energy in rocket propellants (greater energy by weight than explosives, but lower than gasoline), consequences of accidents can be severe. Most space missions have some problems. In 1986, following the Space Shuttle Challenger disaster, American physicist Richard Feynman, having served on the Rogers Commission, estimated that the chance of an unsafe condition for a launch of the Shuttle was very roughly 1%; more recently the historical per person-flight risk in orbital spaceflight has been calculated to be around 2% or 4%.

In May, 2003 the astronaut office made clear its position on the need and feasibility of improving crew safety for future NASA manned missions indicating their "consensus that an order of magnitude reduction in the risk of human life during ascent, compared to the Space Shuttle, is both achievable with current technology and consistent with NASA's focus on steadily improving rocket reliability".

Costs and economics

The costs of rockets can be roughly divided into propellant costs, the costs of obtaining and/or producing the 'dry mass' of the rocket, and the costs of any required support equipment and facilities.

Most of the takeoff mass of a rocket is normally propellant. However propellant is seldom more than a few times more expensive than gasoline per kilogram (as of 2009 gasoline was about $1/kg [$0.45/lb] or less), and although substantial amounts are needed, for all but the very cheapest rockets, it turns out that the propellant costs are usually comparatively small, although not completely negligible. With liquid oxygen costing $0.15 per kilogram ($0.068/lb) and liquid hydrogen $2.20/kg ($1.00/lb), the Space Shuttle in 2009 had a liquid propellant expense of approximately $1.4 million for each launch that cost $450 million from other expenses (with 40% of the mass of propellants used by it being liquids in the external fuel tank, 60% solids in the SRBs).

Even though a rocket's non-propellant, dry mass is often only between 5–20% of total mass, nevertheless this cost dominates. For hardware with the performance used in orbital launch vehicles, expenses of $2000–$10,000+ per kilogram of dry weight are common, primarily from engineering, fabrication, and testing; raw materials amount to typically around 2% of total expense. For most rockets except reusable ones (shuttle engines) the engines need not function more than a few minutes, which simplifies design.

Extreme performance requirements for rockets reaching orbit correlate with high cost, including intensive quality control to ensure reliability despite the limited safety factors allowable for weight reasons. Components produced in small numbers if not individually machined can prevent amortization of R&D and facility costs over mass production to the degree seen in more pedestrian manufacturing. Amongst liquid-fueled rockets, complexity can be influenced by how much hardware must be lightweight, like pressure-fed engines can have two orders of magnitude lesser part count than pump-fed engines but lead to more weight by needing greater tank pressure, most often used in just small maneuvering thrusters as a consequence.

To change the preceding factors for orbital launch vehicles, proposed methods have included mass-producing simple rockets in large quantities or on large scale, or developing reusable rockets meant to fly very frequently to amortize their up-front expense over many payloads, or reducing rocket performance requirements by constructing a non-rocket spacelaunch system for part of the velocity to orbit (or all of it but with most methods involving some rocket use).

The costs of support equipment, range costs and launch pads generally scale up with the size of the rocket, but vary less with launch rate, and so may be considered to be approximately a fixed cost.

Rockets in applications other than launch to orbit (such as military rockets and rocket-assisted take off), commonly not needing comparable performance and sometimes mass-produced, are often relatively inexpensive.

2010s emerging private competition

Further information: Space launch market competition § 2010s: Competition and pricing pressure

Since the early 2010s, new private options for obtaining spaceflight services emerged, bringing substantial price pressure into the existing market.

Protein design

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Protein_design

Protein design is the rational design of new protein molecules to design novel activity, behavior, or purpose, and to advance basic understanding of protein function. Proteins can be designed from scratch (de novo design) or by making calculated variants of a known protein structure and its sequence (termed protein redesign). Rational protein design approaches make protein-sequence predictions that will fold to specific structures. These predicted sequences can then be validated experimentally through methods such as peptide synthesis, site-directed mutagenesis, or artificial gene synthesis.

Rational protein design dates back to the mid-1970s. Recently, however, there were numerous examples of successful rational design of water-soluble and even transmembrane peptides and proteins, in part due to a better understanding of different factors contributing to protein structure stability and development of better computational methods.

Overview and history

The goal in rational protein design is to predict amino acid sequences that will fold to a specific protein structure. Although the number of possible protein sequences is vast, growing exponentially with the size of the protein chain, only a subset of them will fold reliably and quickly to one native state. Protein design involves identifying novel sequences within this subset. The native state of a protein is the conformational free energy minimum for the chain. Thus, protein design is the search for sequences that have the chosen structure as a free energy minimum. In a sense, it is the reverse of protein structure prediction. In design, a tertiary structure is specified, and a sequence that will fold to it is identified. Hence, it is also termed inverse folding. Protein design is then an optimization problem: using some scoring criteria, an optimized sequence that will fold to the desired structure is chosen.

When the first proteins were rationally designed during the 1970s and 1980s, the sequence for these was optimized manually based on analyses of other known proteins, the sequence composition, amino acid charges, and the geometry of the desired structure. The first designed proteins are attributed to Bernd Gutte, who designed a reduced version of a known catalyst, bovine ribonuclease, and tertiary structures consisting of beta-sheets and alpha-helices, including a binder of DDT. Urry and colleagues later designed elastin-like fibrous peptides based on rules on sequence composition. Richardson and coworkers designed a 79-residue protein with no sequence homology to a known protein. In the 1990s, the advent of powerful computers, libraries of amino acid conformations, and force fields developed mainly for molecular dynamics simulations enabled the development of structure-based computational protein design tools. Following the development of these computational tools, great success has been achieved over the last 30 years in protein design. The first protein successfully designed completely de novo was done by Stephen Mayo and coworkers in 1997, and, shortly after, in 1999 Peter S. Kim and coworkers designed dimers, trimers, and tetramers of unnatural right-handed coiled coils. In 2003, David Baker's laboratory designed a full protein to a fold never seen before in nature. Later, in 2008, Baker's group computationally designed enzymes for two different reactions. In 2010, one of the most powerful broadly neutralizing antibodies was isolated from patient serum using a computationally designed protein probe. Due to these and other successes (e.g., see examples below), protein design has become one of the most important tools available for protein engineering. There is great hope that the design of new proteins, small and large, will have uses in biomedicine and bioengineering.

Underlying models of protein structure and function

Protein design programs use computer models of the molecular forces that drive proteins in in vivo environments. In order to make the problem tractable, these forces are simplified by protein design models. Although protein design programs vary greatly, they have to address four main modeling questions: What is the target structure of the design, what flexibility is allowed on the target structure, which sequences are included in the search, and which force field will be used to score sequences and structures.

Target structure

The Top7 protein was one of the first proteins designed for a fold that had never been seen before in nature

Protein function is heavily dependent on protein structure, and rational protein design uses this relationship to design function by designing proteins that have a target structure or fold. Thus, by definition, in rational protein design the target structure or ensemble of structures must be known beforehand. This contrasts with other forms of protein engineering, such as directed evolution, where a variety of methods are used to find proteins that achieve a specific function, and with protein structure prediction where the sequence is known, but the structure is unknown.

Most often, the target structure is based on a known structure of another protein. However, novel folds not seen in nature have been made increasingly possible. Peter S. Kim and coworkers designed trimers and tetramers of unnatural coiled coils, which had not been seen before in nature. The protein Top7, developed in David Baker's lab, was designed completely using protein design algorithms, to a completely novel fold. More recently, Baker and coworkers developed a series of principles to design ideal globular-protein structures based on protein folding funnels that bridge between secondary structure prediction and tertiary structures. These principles, which build on both protein structure prediction and protein design, were used to design five different novel protein topologies.

Sequence space

FSD-1 (shown in blue, PDB id: 1FSV) was the first de novo computational design of a full protein. The target fold was that of the zinc finger in residues 33–60 of the structure of protein Zif268 (shown in red, PDB id: 1ZAA). The designed sequence had very little sequence identity with any known protein sequence.

In rational protein design, proteins can be redesigned from the sequence and structure of a known protein, or completely from scratch in de novo protein design. In protein redesign, most of the residues in the sequence are maintained as their wild-type amino-acid while a few are allowed to mutate. In de novo design, the entire sequence is designed anew, based on no prior sequence.

Both de novo designs and protein redesigns can establish rules on the sequence space: the specific amino acids that are allowed at each mutable residue position. For example, the composition of the surface of the RSC3 probe to select HIV-broadly neutralizing antibodies was restricted based on evolutionary data and charge balancing. Many of the earliest attempts on protein design were heavily based on empiric rules on the sequence space. Moreover, the design of fibrous proteins usually follows strict rules on the sequence space. Collagen-based designed proteins, for example, are often composed of Gly-Pro-X repeating patterns. The advent of computational techniques allows designing proteins with no human intervention in sequence selection.

Structural flexibility

Common protein design programs use rotamer libraries to simplify the conformational space of protein side chains. This animation loops through all the rotamers of the isoleucine amino acid based on the Penultimate Rotamer Library.

In protein design, the target structure (or structures) of the protein are known. However, a rational protein design approach must model some flexibility on the target structure in order to increase the number of sequences that can be designed for that structure and to minimize the chance of a sequence folding to a different structure. For example, in a protein redesign of one small amino acid (such as alanine) in the tightly packed core of a protein, very few mutants would be predicted by a rational design approach to fold to the target structure, if the surrounding side-chains are not allowed to be repacked.

Thus, an essential parameter of any design process is the amount of flexibility allowed for both the side-chains and the backbone. In the simplest models, the protein backbone is kept rigid while some of the protein side-chains are allowed to change conformations. However, side-chains can have many degrees of freedom in their bond lengths, bond angles, and χ dihedral angles. To simplify this space, protein design methods use rotamer libraries that assume ideal values for bond lengths and bond angles, while restricting χ dihedral angles to a few frequently observed low-energy conformations termed rotamers.

Rotamer libraries are derived from the statistical analysis of many protein structures. Backbone-independent rotamer libraries describe all rotamers. Backbone-dependent rotamer libraries, in contrast, describe the rotamers as how likely they are to appear depending on the protein backbone arrangement around the side chain. Most protein design programs use one conformation (e.g., the modal value for rotamer dihedrals in space) or several points in the region described by the rotamer; the OSPREY protein design program, in contrast, models the entire continuous region.

Although rational protein design must preserve the general backbone fold a protein, allowing some backbone flexibility can significantly increase the number of sequences that fold to the structure while maintaining the general fold of the protein. Backbone flexibility is especially important in protein redesign because sequence mutations often result in small changes to the backbone structure. Moreover, backbone flexibility can be essential for more advanced applications of protein design, such as binding prediction and enzyme design. Some models of protein design backbone flexibility include small and continuous global backbone movements, discrete backbone samples around the target fold, backrub motions, and protein loop flexibility.

Energy function

Comparison of various potential energy functions. The most accurate energy are those that use quantum mechanical calculations, but these are too slow for protein design. On the other extreme, heuristic energy functions, are based on statistical terms and are very fast. In the middle are molecular mechanics energy functions that are physically-based but are not as computationally expensive as quantum mechanical simulations.

Rational protein design techniques must be able to discriminate sequences that will be stable under the target fold from those that would prefer other low-energy competing states. Thus, protein design requires accurate energy functions that can rank and score sequences by how well they fold to the target structure. At the same time, however, these energy functions must consider the computational challenges behind protein design. One of the most challenging requirements for successful design is an energy function that is both accurate and simple for computational calculations.

The most accurate energy functions are those based on quantum mechanical simulations. However, such simulations are too slow and typically impractical for protein design. Instead, many protein design algorithms use either physics-based energy functions adapted from molecular mechanics simulation programs, knowledge based energy-functions, or a hybrid mix of both. The trend has been toward using more physics-based potential energy functions.

Physics-based energy functions, such as AMBER and CHARMM, are typically derived from quantum mechanical simulations, and experimental data from thermodynamics, crystallography, and spectroscopy. These energy functions typically simplify physical energy function and make them pairwise decomposable, meaning that the total energy of a protein conformation can be calculated by adding the pairwise energy between each atom pair, which makes them attractive for optimization algorithms. Physics-based energy functions typically model an attractive-repulsive Lennard-Jones term between atoms and a pairwise electrostatics coulombic term between non-bonded atoms.

Water-mediated hydrogen bonds play a key role in protein–protein binding. One such interaction is shown between residues D457, S365 in the heavy chain of the HIV-broadly-neutralizing antibody VRC01 (green) and residues N58 and Y59 in the HIV envelope protein GP120 (purple).

Statistical potentials, in contrast to physics-based potentials, have the advantage of being fast to compute, of accounting implicitly of complex effects and being less sensitive to small changes in the protein structure. These energy functions are based on deriving energy values from frequency of appearance on a structural database.

Protein design, however, has requirements that can sometimes be limited in molecular mechanics force-fields. Molecular mechanics force-fields, which have been used mostly in molecular dynamics simulations, are optimized for the simulation of single sequences, but protein design searches through many conformations of many sequences. Thus, molecular mechanics force-fields must be tailored for protein design. In practice, protein design energy functions often incorporate both statistical terms and physics-based terms. For example, the Rosetta energy function, one of the most-used energy functions, incorporates physics-based energy terms originating in the CHARMM energy function, and statistical energy terms, such as rotamer probability and knowledge-based electrostatics. Typically, energy functions are highly customized between laboratories, and specifically tailored for every design.

Challenges for effective design energy functions

Water makes up most of the molecules surrounding proteins and is the main driver of protein structure. Thus, modeling the interaction between water and protein is vital in protein design. The number of water molecules that interact with a protein at any given time is huge and each one has a large number of degrees of freedom and interaction partners. Instead, protein design programs model most of such water molecules as a continuum, modeling both the hydrophobic effect and solvation polarization.

Individual water molecules can sometimes have a crucial structural role in the core of proteins, and in protein–protein or protein–ligand interactions. Failing to model such waters can result in mispredictions of the optimal sequence of a protein–protein interface. As an alternative, water molecules can be added to rotamers.

As an optimization problem

This animation illustrates the complexity of a protein design search, which typically compares all the rotamer-conformations from all possible mutations at all residues. In this example, the residues Phe36 and His 106 are allowed to mutate to, respectively, the amino acids Tyr and Asn. Phe and Tyr have 4 rotamers each in the rotamer library, while Asn and His have 7 and 8 rotamers, respectively, in the rotamer library (from the Richardson's penultimate rotamer library). The animation loops through all (4 + 4) x (7 + 8) = 120 possibilities. The structure shown is that of myoglobin, PDB id: 1mbn.

The goal of protein design is to find a protein sequence that will fold to a target structure. A protein design algorithm must, thus, search all the conformations of each sequence, with respect to the target fold, and rank sequences according to the lowest-energy conformation of each one, as determined by the protein design energy function. Thus, a typical input to the protein design algorithm is the target fold, the sequence space, the structural flexibility, and the energy function, while the output is one or more sequences that are predicted to fold stably to the target structure.

The number of candidate protein sequences, however, grows exponentially with the number of protein residues; for example, there are 20¹⁰⁰ protein sequences of length 100. Furthermore, even if amino acid side-chain conformations are limited to a few rotamers (see Structural flexibility), this results in an exponential number of conformations for each sequence. Thus, in our 100 residue protein, and assuming that each amino acid has exactly 10 rotamers, a search algorithm that searches this space will have to search over 200¹⁰⁰ protein conformations.

The most common energy functions can be decomposed into pairwise terms between rotamers and amino acid types, which casts the problem as a combinatorial one, and powerful optimization algorithms can be used to solve it. In those cases, the total energy of each conformation belonging to each sequence can be formulated as a sum of individual and pairwise terms between residue positions. If a designer is interested only in the best sequence, the protein design algorithm only requires the lowest-energy conformation of the lowest-energy sequence. In these cases, the amino acid identity of each rotamer can be ignored and all rotamers belonging to different amino acids can be treated the same. Let r_i be a rotamer at residue position i in the protein chain, and E(r_i) the potential energy between the internal atoms of the rotamer. Let E(r_i, r_j) be the potential energy between r_i and rotamer r_j at residue position j. Then, we define the optimization problem as one of finding the conformation of minimum energy (E_T):

${\displaystyle \min E_{T}=\sum _{i}{\Big [}E_{i}(r_{i})+\sum _{i\neq j}E_{ij}(r_{i},r_{j}){\Big ]}\,}$

1

The problem of minimizing E_T is an NP-hard problem. Even though the class of problems is NP-hard, in practice many instances of protein design can be solved exactly or optimized satisfactorily through heuristic methods.

Algorithms

Several algorithms have been developed specifically for the protein design problem. These algorithms can be divided into two broad classes: exact algorithms, such as dead-end elimination, that lack runtime guarantees but guarantee the quality of the solution; and heuristic algorithms, such as Monte Carlo, that are faster than exact algorithms but have no guarantees on the optimality of the results. Exact algorithms guarantee that the optimization process produced the optimal according to the protein design model. Thus, if the predictions of exact algorithms fail when these are experimentally validated, then the source of error can be attributed to the energy function, the allowed flexibility, the sequence space or the target structure (e.g., if it cannot be designed for).

Some protein design algorithms are listed below. Although these algorithms address only the most basic formulation of the protein design problem, Equation (1), when the optimization goal changes because designers introduce improvements and extensions to the protein design model, such as improvements to the structural flexibility allowed (e.g., protein backbone flexibility) or including sophisticated energy terms, many of the extensions on protein design that improve modeling are built atop these algorithms. For example, Rosetta Design incorporates sophisticated energy terms, and backbone flexibility using Monte Carlo as the underlying optimizing algorithm. OSPREY's algorithms build on the dead-end elimination algorithm and A* to incorporate continuous backbone and side-chain movements. Thus, these algorithms provide a good perspective on the different kinds of algorithms available for protein design.

In July 2020 scientists reported the development of an AI-based process using genome databases for evolution-based designing of novel proteins. They used deep learning to identify design-rules.

With mathematical guarantees

Dead-end elimination

Main article: Dead-end elimination

The dead-end elimination (DEE) algorithm reduces the search space of the problem iteratively by removing rotamers that can be provably shown to be not part of the global lowest energy conformation (GMEC). On each iteration, the dead-end elimination algorithm compares all possible pairs of rotamers at each residue position, and removes each rotamer r′_i that can be shown to always be of higher energy than another rotamer r_i and is thus not part of the GMEC:

${\displaystyle E(r_{i}^{\prime })+\sum _{j\neq i}\min _{r_{j}}E(r_{i}^{\prime },r_{j})>E(r_{i})+\sum _{j\neq i}\max _{r_{j}}E(r_{i},r_{j})}$

Other powerful extensions to the dead-end elimination algorithm include the pairs elimination criterion, and the generalized dead-end elimination criterion. This algorithm has also been extended to handle continuous rotamers with provable guarantees.

Although the Dead-end elimination algorithm runs in polynomial time on each iteration, it cannot guarantee convergence. If, after a certain number of iterations, the dead-end elimination algorithm does not prune any more rotamers, then either rotamers have to be merged or another search algorithm must be used to search the remaining search space. In such cases, the dead-end elimination acts as a pre-filtering algorithm to reduce the search space, while other algorithms, such as A*, Monte Carlo, Linear Programming, or FASTER are used to search the remaining search space.

Branch and bound

Main article: Branch and bound

The protein design conformational space can be represented as a tree, where the protein residues are ordered in an arbitrary way, and the tree branches at each of the rotamers in a residue. Branch and bound algorithms use this representation to efficiently explore the conformation tree: At each branching, branch and bound algorithms bound the conformation space and explore only the promising branches.

A popular search algorithm for protein design is the A* search algorithm. A* computes a lower-bound score on each partial tree path that lower bounds (with guarantees) the energy of each of the expanded rotamers. Each partial conformation is added to a priority queue and at each iteration the partial path with the lowest lower bound is popped from the queue and expanded. The algorithm stops once a full conformation has been enumerated and guarantees that the conformation is the optimal.

The A* score f in protein design consists of two parts, f=g+h. g is the exact energy of the rotamers that have already been assigned in the partial conformation. h is a lower bound on the energy of the rotamers that have not yet been assigned. Each is designed as follows, where d is the index of the last assigned residue in the partial conformation.

${\displaystyle g=\sum _{i=1}^{d}(E(r_{i})+\sum _{j=i+1}^{d}E(r_{i},r_{j}))}$

${\displaystyle h=\sum _{j=d+1}^{n}[\min _{r_{j}}(E(r_{j})+\sum _{i=1}^{d}E(r_{i},r_{j})+\sum _{k=j+1}^{n}\min _{r_{k}}E(r_{j},r_{k}))]}$

Integer linear programming

Further information: Linear programming § Integer unknowns, and Integer programming

The problem of optimizing E_T (Equation (1)) can be easily formulated as an integer linear program (ILP). One of the most powerful formulations uses binary variables to represent the presence of a rotamer and edges in the final solution, and constraints the solution to have exactly one rotamer for each residue and one pairwise interaction for each pair of residues:

${\displaystyle \ \min \sum _{i}\sum _{r_{i}}E_{i}(r_{i})q_{i}(r_{i})+\sum _{j\neq i}\sum _{r_{j}}E_{ij}(r_{i},r_{j})q_{ij}(r_{i},r_{j})\,}$

s.t.

${\displaystyle \sum _{r_{i}}q_{i}(r_{i})=1,\ \forall i}$

${\displaystyle \sum _{r_{j}}q_{ij}(r_{i},r_{j})=q_{i}(r_{i}),\forall i,r_{i},j}$

${\displaystyle q_{i},q_{ij}\in \{0,1\}}$

ILP solvers, such as CPLEX, can compute the exact optimal solution for large instances of protein design problems. These solvers use a linear programming relaxation of the problem, where q_i and q_ij are allowed to take continuous values, in combination with a branch and cut algorithm to search only a small portion of the conformation space for the optimal solution. ILP solvers have been shown to solve many instances of the side-chain placement problem.

Message-passing based approximations to the linear programming dual

ILP solvers depend on linear programming (LP) algorithms, such as the Simplex or barrier-based methods to perform the LP relaxation at each branch. These LP algorithms were developed as general-purpose optimization methods and are not optimized for the protein design problem (Equation (1)). In consequence, the LP relaxation becomes the bottleneck of ILP solvers when the problem size is large. Recently, several alternatives based on message-passing algorithms have been designed specifically for the optimization of the LP relaxation of the protein design problem. These algorithms can approximate both the dual or the primal instances of the integer programming, but in order to maintain guarantees on optimality, they are most useful when used to approximate the dual of the protein design problem, because approximating the dual guarantees that no solutions are missed. Message-passing based approximations include the tree reweighted max-product message passing algorithm, and the message passing linear programming algorithm.

Optimization algorithms without guarantees

Monte Carlo and simulated annealing

Monte Carlo is one of the most widely used algorithms for protein design. In its simplest form, a Monte Carlo algorithm selects a residue at random, and in that residue a randomly chosen rotamer (of any amino acid) is evaluated. The new energy of the protein, E_new is compared against the old energy E_old and the new rotamer is accepted with a probability of:

${\displaystyle p=e^{-\beta (E_{\text{new}}-E_{\text{old}}))},}$

where β is the Boltzmann constant and the temperature T can be chosen such that in the initial rounds it is high and it is slowly annealed to overcome local minima.

FASTER

The FASTER algorithm uses a combination of deterministic and stochastic criteria to optimize amino acid sequences. FASTER first uses DEE to eliminate rotamers that are not part of the optimal solution. Then, a series of iterative steps optimize the rotamer assignment.

Belief propagation

In belief propagation for protein design, the algorithm exchanges messages that describe the belief that each residue has about the probability of each rotamer in neighboring residues. The algorithm updates messages on every iteration and iterates until convergence or until a fixed number of iterations. Convergence is not guaranteed in protein design. The message m_{i→ j}(r_j that a residue i sends to every rotamer (r_j at neighboring residue j is defined as:

${\displaystyle m_{i\to j}(r_{j})=\max _{r_{i}}{\Big (}e^{\frac {-E_{i}(r_{i})-E_{ij}(r_{i},r_{j})}{T}}{\Big )}\prod _{k\in N(i)\backslash j}m_{k\to i(r_{i})}}$

Both max-product and sum-product belief propagation have been used to optimize protein design.

Applications and examples of designed proteins

Enzyme design

The design of new enzymes is a use of protein design with huge bioengineering and biomedical applications. In general, designing a protein structure can be different from designing an enzyme, because the design of enzymes must consider many states involved in the catalytic mechanism. However protein design is a prerequisite of de novo enzyme design because, at the very least, the design of catalysts requires a scaffold in which the catalytic mechanism can be inserted.

Great progress in de novo enzyme design, and redesign, was made in the first decade of the 21st century. In three major studies, David Baker and coworkers de novo designed enzymes for the retro-aldol reaction, a Kemp-elimination reaction, and for the Diels-Alder reaction. Furthermore, Stephen Mayo and coworkers developed an iterative method to design the most efficient known enzyme for the Kemp-elimination reaction. Also, in the laboratory of Bruce Donald, computational protein design was used to switch the specificity of one of the protein domains of the nonribosomal peptide synthetase that produces Gramicidin S, from its natural substrate phenylalanine to other noncognate substrates including charged amino acids; the redesigned enzymes had activities close to those of the wild-type.

Design for affinity

Protein–protein interactions are involved in most biotic processes. Many of the hardest-to-treat diseases, such as Alzheimer's, many forms of cancer (e.g., TP53), and human immunodeficiency virus (HIV) infection involve protein–protein interactions. Thus, to treat such diseases, it is desirable to design protein or protein-like therapeutics that bind one of the partners of the interaction and, thus, disrupt the disease-causing interaction. This requires designing protein-therapeutics for affinity toward its partner.

Protein–protein interactions can be designed using protein design algorithms because the principles that rule protein stability also rule protein–protein binding. Protein–protein interaction design, however, presents challenges not commonly present in protein design. One of the most important challenges is that, in general, the interfaces between proteins are more polar than protein cores, and binding involves a tradeoff between desolvation and hydrogen bond formation. To overcome this challenge, Bruce Tidor and coworkers developed a method to improve the affinity of antibodies by focusing on electrostatic contributions. They found that, for the antibodies designed in the study, reducing the desolvation costs of the residues in the interface increased the affinity of the binding pair.

Scoring binding predictions

Protein design energy functions must be adapted to score binding predictions because binding involves a trade-off between the lowest-energy conformations of the free proteins (E_P and E_L) and the lowest-energy conformation of the bound complex (E_PL):

${\displaystyle \Delta _{G}=E_{PL}-E_{P}-E_{L}}$.

The K* algorithm approximates the binding constant of the algorithm by including conformational entropy into the free energy calculation. The K* algorithm considers only the lowest-energy conformations of the free and bound complexes (denoted by the sets P, L, and PL) to approximate the partition functions of each complex:

${\displaystyle K^{*}={\frac {\sum \limits _{x\in PL}e^{-E(x)/RT}}{\sum \limits _{x\in P}e^{-E(x)/RT}\sum \limits _{x\in L}e^{-E(x)/RT}}}}$

Design for specificity

The design of protein–protein interactions must be highly specific because proteins can interact with a large number of proteins; successful design requires selective binders. Thus, protein design algorithms must be able to distinguish between on-target (or positive design) and off-target binding (or negative design). One of the most prominent examples of design for specificity is the design of specific bZIP-binding peptides by Amy Keating and coworkers for 19 out of the 20 bZIP families; 8 of these peptides were specific for their intended partner over competing peptides. Further, positive and negative design was also used by Anderson and coworkers to predict mutations in the active site of a drug target that conferred resistance to a new drug; positive design was used to maintain wild-type activity, while negative design was used to disrupt binding of the drug. Recent computational redesign by Costas Maranas and coworkers was also capable of experimentally switching the cofactor specificity of Candida boidinii xylose reductase from NADPH to NADH.

Protein resurfacing

Protein resurfacing consists of designing a protein's surface while preserving the overall fold, core, and boundary regions of the protein intact. Protein resurfacing is especially useful to alter the binding of a protein to other proteins. One of the most important applications of protein resurfacing was the design of the RSC3 probe to select broadly neutralizing HIV antibodies at the NIH Vaccine Research Center. First, residues outside of the binding interface between the gp120 HIV envelope protein and the formerly discovered b12-antibody were selected to be designed. Then, the sequence spaced was selected based on evolutionary information, solubility, similarity with the wild-type, and other considerations. Then the RosettaDesign software was used to find optimal sequences in the selected sequence space. RSC3 was later used to discover the broadly neutralizing antibody VRC01 in the serum of a long-term HIV-infected non-progressor individual.

Design of globular proteins

Globular proteins are proteins that contain a hydrophobic core and a hydrophilic surface. Globular proteins often assume a stable structure, unlike fibrous proteins, which have multiple conformations. The three-dimensional structure of globular proteins is typically easier to determine through X-ray crystallography and nuclear magnetic resonance than both fibrous proteins and membrane proteins, which makes globular proteins more attractive for protein design than the other types of proteins. Most successful protein designs have involved globular proteins. Both RSD-1, and Top7 were de novo designs of globular proteins. Five more protein structures were designed, synthesized, and verified in 2012 by the Baker group. These new proteins serve no biotic function, but the structures are intended to act as building-blocks that can be expanded to incorporate functional active sites. The structures were found computationally by using new heuristics based on analyzing the connecting loops between parts of the sequence that specify secondary structures.

Design of membrane proteins

Several transmembrane proteins have been successfully designed, along with many other membrane-associated peptides and proteins. Recently, Costas Maranas and his coworkers developed an automated tool to redesign the pore size of Outer Membrane Porin Type-F (OmpF) from E.coli to any desired sub-nm size and assembled them in membranes to perform precise angstrom scale separation.

Other applications

One of the most desirable uses for protein design is for biosensors, proteins that will sense the presence of specific compounds. Some attempts in the design of biosensors include sensors for unnatural molecules including TNT. More recently, Kuhlman and coworkers designed a biosensor of the PAK1.