Metamaterial cloaking is the usage of metamaterials in an invisibility cloak. This is accomplished by manipulating the paths traversed by light through a novel optical material. Metamaterials direct and control the propagation and transmission of specified parts of the light spectrum and demonstrate the potential to render an object seemingly invisible. Metamaterial cloaking, based on transformation optics, describes the process of shielding something from view by controlling electromagnetic radiation. Objects in the defined location are still present, but incident waves are guided around them without being affected by the object itself.
Electromagnetic metamaterials
Electromagnetic metamaterials respond to chosen parts of radiated light, also known as the electromagnetic spectrum, in a manner that is difficult or impossible to achieve with natural materials. In other words, these metamaterials can be further defined as artificially structured composite materials, which exhibit interaction with light usually not available in nature (electromagnetic interactions). At the same time, metamaterials have the potential to be engineered and constructed with desirable properties that fit a specific need. That need will be determined by the particular application.
The artificial structure for cloaking applications is a lattice design – a sequentially repeating network – of identical elements. Additionally, for microwave frequencies, these materials are analogous to crystals for optics. Also, a metamaterial is composed of a sequence of elements and spacings, which are much smaller than the selected wavelength of light. The selected wavelength could be radio frequency, microwave, or other radiations, now just beginning to reach into the visible frequencies. Macroscopic properties can be directly controlled by adjusting characteristics of the rudimentary elements, and their arrangement on, or throughout the material. Moreover, these metamaterials are a basis for building very small cloaking devices in anticipation of larger devices, adaptable to a broad spectrum of radiated light.
Hence, although light consists of an electric field and a magnetic field, ordinary optical materials, such as optical microscope lenses, have a strong reaction only to the electric field. The corresponding magnetic interaction is essentially nil. This results in only the most common optical effects, such as ordinary refraction with common diffraction limitations in lenses and imaging.
Since the beginning of optical sciences, centuries ago, the ability to control the light with materials has been limited to these common optical effects. Metamaterials, on the other hand, are capable of a very strong interaction, or coupling, with the magnetic component of light. Therefore, the range of response to radiated light is expanded beyond the ordinary optical limitations that are described by the sciences of physical optics and optical physics. In addition, as artificially constructed materials, both the magnetic and electric components of the radiated light can be controlled at will, in any desired fashion as it travels, or more accurately propagates, through the material. This is because a metamaterial's behavior is typically formed from individual components, and each component responds independently to a radiated spectrum of light. At this time, however, metamaterials are limited. Cloaking across a broad spectrum of frequencies has not been achieved, including the visible spectrum. Dissipation, absorption, and dispersion are also current drawbacks, but this field is still in its optimistic infancy.
Metamaterials and transformation optics
The field of transformation optics is founded on the effects produced by metamaterials.
Transformation optics has its beginnings in the conclusions of two research endeavors. They were published on May 25, 2006, in the same issue of Science, a peer reviewed journal. The two papers are tenable theories on bending or distorting light to electromagnetically conceal an object. Both papers notably map the initial configuration of the electromagnetic fields on to a Cartesian mesh. Twisting the Cartesian mesh, in essence, transforms the coordinates of the electromagnetic fields, which in turn conceal a given object. Hence, with these two papers, transformation optics is born.
Transformation optics subscribes to the capability of bending light, or electromagnetic waves and energy, in any preferred or desired fashion, for a desired application. Maxwell's equations do not vary even though coordinates transform. Instead it is the values of the chosen parameters of the materials which "transform", or alter, during a certain time period. So, transformation optics developed from the capability to choose the parameters for a given material. Hence, since Maxwell's equations retain the same form, it is the successive values of the parameters, permittivity and permeability, which change over time. Furthermore, permittivity and permeability are in a sense responses to the electric and magnetic fields of a radiated light source respectively, among other descriptions. The precise degree of electric and magnetic response can be controlled in a metamaterial, point by point. Since so much control can be maintained over the responses of the material, this leads to an enhanced and highly flexible gradient-index material. Conventionally predetermined refractive index of ordinary materials instead become independent spatial gradients in a metamaterial, which can be controlled at will. Therefore, transformation optics is a new method for creating novel and unique optical devices.
Science of cloaking devices
The purpose of a cloaking device is to hide something, so that a defined region of space is invisibly isolated from passing electromagnetic fields (or sound waves), as with Metamaterial cloaking.
Cloaking objects, or making them appear invisible with metamaterials, is roughly analogous to a magician's sleight of hand, or his tricks with mirrors. The object or subject doesn't really disappear; the vanishing is an illusion. With the same goal, researchers employ metamaterials to create directed blind spots by deflecting certain parts of the light spectrum (electromagnetic spectrum). It is the light spectrum, as the transmission medium, that determines what the human eye can see.
In other words, light is refracted or reflected determining the view, color, or illusion that is seen. The visible extent of light is seen in a chromatic spectrum such as the rainbow. However, visible light is only part of a broad spectrum, which extends beyond the sense of sight. For example, there are other parts of the light spectrum which are in common use today. The microwave spectrum is employed by radar, cell phones, and wireless Internet. The infrared spectrum is used for thermal imaging technologies, which can detect a warm body amidst a cooler night time environment, and infrared illumination is combined with specialized digital cameras for night vision. Astronomers employ the terahertz band for submillimeter observations to answer deep cosmological questions.
Furthermore, electromagnetic energy is light energy, but only a small part of it is visible light. This energy travels in waves. Shorter wavelengths, such as visible light and infrared, carry more energy per photon than longer waves, such as microwaves and radio waves. For the sciences, the light spectrum is known as the electromagnetic spectrum.
The properties of optics and light
Prisms, mirrors, and lenses have a long history of altering the diffracted visible light that surrounds all. However, the control exhibited by these ordinary materials is limited. Moreover, the one material which is common among these three types of directors of light is conventional glass. Hence, these familiar technologies are constrained by the fundamental, physical laws of optics. With metamaterials in general, and the cloaking technology in particular, it appears these barriers disintegrate with advancements in materials and technologies never before realized in the natural physical sciences. These unique materials became notable because electromagnetic radiation can be bent, reflected, or skewed in new ways. The radiated light could even be slowed or captured before transmission. In other words, new ways to focus and project light and other radiation are being developed. Furthermore, the expanded optical powers presented in the science of cloaking objects appear to be technologically beneficial across a wide spectrum of devices already in use. This means that every device with basic functions that rely on interaction with the radiated electromagnetic spectrum could technologically advance. With these beginning steps a whole new class of optics has been established.
Interest in the properties of optics and light
Interest in the properties of optics, and light, date back to almost 2000 years to Ptolemy (AD 85 – 165). In his work entitled Optics, he writes about the properties of light, including reflection, refraction, and color. He developed a simplified equation for refraction without trigonometric functions. About 800 years later, in AD 984, Ibn Sahl discovered a law of refraction mathematically equivalent to Snell's law. He was followed by the most notable Islamic scientist, Ibn Al-Haytham (c.965–1039), who is considered to be "one of the few most outstanding figures in optics in all times." He made significant advances in the science of physics in general, and optics in particular. He anticipated the universal laws of light articulated by seventeenth century scientists by hundreds of years.
In the seventeenth century both Willebrord Snellius and Descartes were credited with discovering the law of refraction. It was Snellius who noted that Ptolemy's equation for refraction was inexact. Consequently, these laws have been passed along, unchanged for about 400 years, like the laws of gravity.
Perfect cloak and theory
Electromagnetic radiation and matter have a symbiotic relationship. Radiation does not simply act on a material, nor is it simply acted upon by a given material. Radiation interacts with matter. Cloaking applications which employ metamaterials alter how objects interact with the electromagnetic spectrum. The guiding vision for the metamaterial cloak is a device that directs the flow of light smoothly around an object, like water flowing past a rock in a stream, without reflection, rendering the object invisible. In reality, the simple cloaking devices of the present are imperfect, and have limitations. One challenge up to the present date has been the inability of metamaterials, and cloaking devices, to interact at frequencies, or wavelengths, within the visible light spectrum.
Challenges presented by the first cloaking device
The principle of cloaking, with a cloaking device, was first proved (demonstrated) at frequencies in the microwave radiation band on October 19, 2006. This demonstration used a small cloaking device. Its height was less than one half inch (< 13 mm) and its diameter five inches (125 mm), and it successfully diverted microwaves around itself. The object to be hidden from view, a small cylinder, was placed in the center of the device. The invisibility cloak deflected microwave beams so they flowed around the cylinder inside with only minor distortion, making it appear almost as if nothing were there at all.
Such a device typically involves surrounding the object to be cloaked with a shell which affects the passage of light near it. There was reduced reflection of electromagnetic waves (microwaves), from the object. Unlike a homogeneous natural material with its material properties the same everywhere, the cloak's material properties vary from point to point, with each point designed for specific electromagnetic interactions (inhomogeneity), and are different in different directions (anisotropy). This accomplishes a gradient in the material properties. The associated report was published in the journal Science.
Although a successful demonstration, three notable limitations can be shown. First, since its effectiveness was only in the microwave spectrum the small object is somewhat invisible only at microwave frequencies. This means invisibility had not been achieved for the human eye, which sees only within the visible spectrum. This is because the wavelengths of the visible spectrum are tangibly shorter than microwaves. However, this was considered the first step toward a cloaking device for visible light, although more advanced nanotechnology-related techniques would be needed due to light's short wavelengths. Second, only small objects can be made to appear as the surrounding air. In the case of the 2006 proof of cloaking demonstration, the hidden from view object, a copper cylinder, would have to be less than five inches in diameter, and less than one half inch tall. Third, cloaking can only occur over a narrow frequency band, for any given demonstration. This means that a broad band cloak, which works across the electromagnetic spectrum, from radio frequencies to microwave to the visible spectrum, and to x-ray, is not available at this time. This is due to the dispersive nature of present-day metamaterials. The coordinate transformation (transformation optics) requires extraordinary material parameters that are only approachable through the use of resonant elements, which are inherently narrow band, and dispersive at resonance.
Usage of metamaterials
At the very beginning of the new millennium, metamaterials were established as an extraordinary new medium, which expanded control capabilities over matter. Hence, metamaterials are applied to cloaking applications for a few reasons. First, the parameter known as material response has broader range. Second, the material response can be controlled at will.
Third, optical components, such as lenses, respond within a certain defined range to light. As stated earlier – the range of response has been known, and studied, going back to Ptolemy – eighteen hundred years ago. The range of response could not be effectively exceeded, because natural materials proved incapable of doing so. In scientific studies and research, one way to communicate the range of response is the refractive index of a given optical material. Every natural material so far only allows for a positive refractive index. Metamaterials, on the other hand, are an innovation that are able to achieve negative refractive index, zero refractive index, and fractional values in between zero and one. Hence, metamaterials extend the material response, among other capabilities. However, negative refraction is not the effect that creates invisibility-cloaking. It is more accurate to say that gradations of refractive index, when combined, create invisibility-cloaking. Fourth, and finally, metamaterials demonstrate the capability to deliver chosen responses at will.
Device
Before actually building the device, theoretical studies were conducted. The following is one of two studies accepted simultaneously by a scientific journal, as well being distinguished as one of the first published theoretical works for an invisibility cloak.
Controlling electromagnetic fields
The exploitation of "light", the electromagnetic spectrum, is accomplished with common objects and materials which control and direct the electromagnetic fields. For example, a glass lens in a camera is used to produce an image, a metal cage may be used to screen sensitive equipment, and radio antennas are designed to transmit and receive daily FM broadcasts. Homogeneous materials, which manipulate or modulate electromagnetic radiation, such as glass lenses, are limited in the upper limit of refinements to correct for aberrations. Combinations of inhomogeneous lens materials are able to employ gradient refractive indices, but the ranges tend to be limited.
Metamaterials were introduced about a decade ago, and these expand control of parts of the electromagnetic spectrum; from microwave, to terahertz, to infrared. Theoretically, metamaterials, as a transmission medium, will eventually expand control and direction of electromagnetic fields into the visible spectrum. Hence, a design strategy was introduced in 2006, to show that a metamaterial can be engineered with arbitrarily assigned positive or negative values of permittivity and permeability, which can also be independently varied at will. Then direct control of electromagnetic fields becomes possible, which is relevant to novel and unusual lens design, as well as a component of the scientific theory for cloaking of objects from electromagnetic detection.
Each component responds independently to a radiated electromagnetic wave as it travels through the material, resulting in electromagnetic inhomogeneity for each component. Each component has its own response to the external electric and magnetic fields of the radiated source. Since these components are smaller than the radiated wavelength it is understood that a macroscopic view includes an effective value for both permittivity and permeability. These materials obey the laws of physics, but behave differently from normal materials. Metamaterials are artificial materials engineered to provide properties which "may not be readily available in nature". These materials usually gain their properties from structure rather than composition, using the inclusion of small inhomogeneities to enact effective macroscopic behavior.
The structural units of metamaterials can be tailored in shape and size. Their composition, and their form or structure, can be finely adjusted. Inclusions can be designed, and then placed at desired locations in order to vary the function of a given material. As the lattice is constant, the cells are smaller than the radiated light.
The design strategy has at its core inhomogeneous composite metamaterials which direct, at will, conserved quantities of electromagnetism. These quantities are specifically, the electric displacement field D, the magnetic field intensity B, and the Poynting vector S. Theoretically, when regarding the conserved quantities, or fields, the metamaterial exhibits a twofold capability. First, the fields can be concentrated in a given direction. Second, they can be made to avoid or surround objects, returning without perturbation to their original path. These results are consistent with Maxwell's equations and are more than only ray approximation found in geometrical optics. Accordingly, in principle, these effects can encompass all forms of electromagnetic radiation phenomena on all length scales.
The hypothesized design strategy begins with intentionally choosing a configuration of an arbitrary number of embedded sources. These sources become localized responses of permittivity, ε, and magnetic permeability, μ. The sources are embedded in an arbitrarily selected transmission medium with dielectric and magnetic characteristics. As an electromagnetic system the medium can then be schematically represented as a grid.
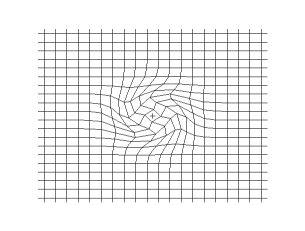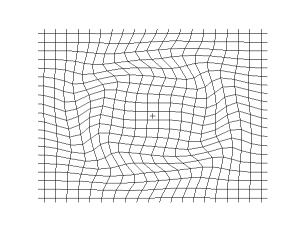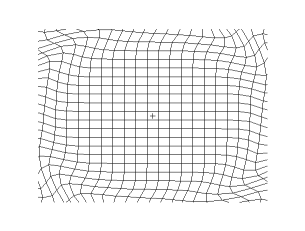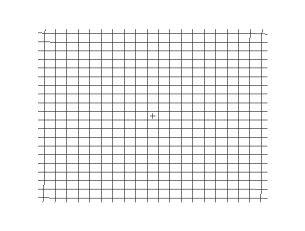
The first requirement might be to move a uniform electric field through space, but in a definite direction, which avoids an object or obstacle. Next remove and embed the system in an elastic medium that can be warped, twisted, pulled or stretched as desired. The initial condition of the fields is recorded on a Cartesian mesh. As the elastic medium is distorted in one, or combination, of the described possibilities, the same pulling and stretching process is recorded by the Cartesian mesh. The same set of contortions can now be recorded, occurring as coordinate transformation:
- a (x,y,z), b (x,y,z), c (x,y,z), d (x,y,z) ....
Hence, the permittivity, ε, and permeability, µ, is proportionally calibrated by a common factor. This implies that less precisely, the same occurs with the refractive index. Renormalized values of permittivity and permeability are applied in the new coordinate system. For the renormalization equations see ref. #.
Application to cloaking devices
Given the above parameters of operation, the system, a metamaterial, can now be shown to be able to conceal an object of arbitrary size. Its function is to manipulate incoming rays, which are about to strike the object. These incoming rays are instead electromagnetically steered around the object by the metamaterial, which then returns them to their original trajectory. As part of the design it can be assumed that no radiation leaves the concealed volume of space, and no radiation can enter the space. As illustrated by the function of the metamaterial, any radiation attempting to penetrate is steered around the space or the object within the space, returning to the initial direction. It appears to any observer that the concealed volume of space is empty, even with an object present there. An arbitrary object may be hidden because it remains untouched by external radiation.
A sphere with radius R1 is chosen as the object to be hidden. The cloaking region is to be contained within the annulus R1 < r < R2. A simple transformation that achieves the desired result can be found by taking all fields in the region r < R2 and compressing them into the region R1 < r < R2. The coordinate transformations do not alter Maxwell's equations. Only the values of ε′ and µ′ change over time.
Cloaking hurdles
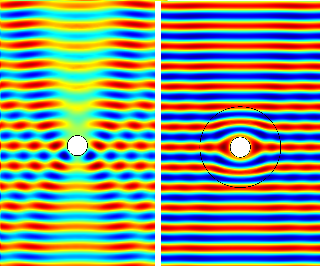
There are issues to be dealt with to achieve invisibility cloaking. One issue, related to ray tracing, is the anisotropic effects of the material on the electromagnetic rays entering the "system". Parallel bundles of rays, (see above image), headed directly for the center are abruptly curved and, along with neighboring rays, are forced into tighter and tighter arcs. This is due to rapid changes in the now shifting and transforming permittivity ε′ and permeability µ′. The second issue is that, while it has been discovered that the selected metamaterials are capable of working within the parameters of the anisotropic effects and the continual shifting of ε′ and µ′, the values for ε′ and µ′ cannot be very large or very small. The third issue is that the selected metamaterials are currently unable to achieve broad, frequency spectrum capabilities. This is because the rays must curve around the "concealed" sphere, and therefore have longer trajectories than traversing free space, or air. However, the rays must arrive around the other side of the sphere in phase with the beginning radiated light. If this is happening then the phase velocity exceeds the velocity of light in a vacuum, which is the speed limit of the universe. (Note, this does not violate the laws of physics). And, with a required absence of frequency dispersion, the group velocity will be identical with phase velocity. In the context of this experiment, group velocity can never exceed the velocity of light, hence the analytical parameters are effective for only one frequency.
Optical conformal mapping and ray tracing in transformation media
The goal then is to create no discernible difference between a concealed volume of space and the propagation of electromagnetic waves through empty space. It would appear that achieving a perfectly concealed (100%) hole, where an object could be placed and hidden from view, is not probable. The problem is the following: in order to carry images, light propagates in a continuous range of directions. The scattering data of electromagnetic waves, after bouncing off an object or hole, is unique compared to light propagating through empty space, and is therefore easily perceived. Light propagating through empty space is consistent only with empty space. This includes microwave frequencies.
Although mathematical reasoning shows that perfect concealment is not probable because of the wave nature of light, this problem does not apply to electromagnetic rays, i.e., the domain of geometrical optics. Imperfections can be made arbitrarily, and exponentially small for objects that are much larger than the wavelength of light.
Mathematically, this implies n < 1, because the rays follow the shortest path and hence in theory create a perfect concealment. In practice, a certain amount of acceptable visibility occurs, as noted above. The range of the refractive index of the dielectric (optical material) needs to be across a wide spectrum to achieve concealment, with the illusion created by wave propagation across empty space. These places where n < 1 would be the shortest path for the ray around the object without phase distortion. Artificial propagation of empty space could be reached in the microwave-to-terahertz range. In stealth technology, impedance matching could result in absorption of beamed electromagnetic waves rather than reflection, hence, evasion of detection by radar. These general principles can also be applied to sound waves, where the index n describes the ratio of the local phase velocity of the wave to the bulk value. Hence, it would be useful to protect a space from any sound sourced detection. This also implies protection from sonar. Furthermore, these general principles are applicable in diverse fields such as electrostatics, fluid mechanics, classical mechanics, and quantum chaos.
Mathematically, it can be shown that the wave propagation is indistinguishable from empty space where light rays propagate along straight lines. The medium performs an optical conformal mapping to empty space.
Microwave frequencies
The next step, then, is to actually conceal an object by controlling electromagnetic fields. Now, the demonstrated and theoretical ability for controlled electromagnetic fields has opened a new field, transformation optics. This nomenclature is derived from coordinate transformations used to create variable pathways for the propagation of light through a material. This demonstration is based on previous theoretical prescriptions, along with the accomplishment of the prism experiment. One possible application of transformation optics and materials is electromagnetic cloaking for the purpose of rendering a volume or object undetectable to incident radiation, including radiated probing.
This demonstration, for the first time, of actually concealing an object with electromagnetic fields, uses the method of purposely designed spatial variation. This is an effect of embedding purposely designed electromagnetic sources in the metamaterial.
As discussed earlier, the fields produced by the metamaterial are compressed into a shell (coordinate transformations) surrounding the now concealed volume. Earlier this was supported theory; this experiment demonstrated the effect actually occurs. Maxwell's equations are scalar when applying transformational coordinates, only the permittivity tensor and permeability tensor are affected, which then become spatially variant, and directionally dependent along different axes. The researchers state:
By implementing these complex material properties, the concealed volume plus the cloak appear to have the properties of free space when viewed externally. The cloak thus neither scatters waves nor imparts a shadow in the either of which would enable the cloak to be detected. Other approaches to invisibility either rely on the reduction of backscatter or make use of a resonance in which the properties of the cloaked object and the must be carefully matched. ...Advances in the development of [negative index metamaterials], especially with respect to gradient index lenses, have made the physical realization of the specified complex material properties feasible. We implemented a two-dimensional (2D) cloak because its fabrication and measurement requirements were simpler than those of a 3D cloak.
Before the actual demonstration, the experimental limits of the transformational fields were computationally determined, in addition to simulations, as both were used to determine the effectiveness of the cloak.
A month prior to this demonstration, the results of an experiment to spatially map the internal and external electromagnetic fields of negative refractive metamaterial was published in September 2006. This was innovative because prior to this the microwave fields were measured only externally. In this September experiment the permittivity and permeability of the microstructures (instead of external macrostructure) of the metamaterial samples were measured, as well as the scattering by the two-dimensional negative index metamaterials. This gave an average effective refractive index, which results in assuming homogeneous metamaterial.
Employing this technique for this experiment, spatial mapping of phases and amplitudes of the microwave radiations interacting with metamaterial samples was conducted. The performance of the cloak was confirmed by comparing the measured field maps to simulations.
For this demonstration, the concealed object was a conducting cylinder at the inner radius of the cloak. As the largest possible object designed for this volume of space, it has the most substantial scattering properties. The conducting cylinder was effectively concealed in two dimensions.
Infrared frequencies
The definition optical frequency, in metamaterials literature, ranges from far infrared, to near infrared, through the visible spectrum, and includes at least a portion of ultra-violet. To date when literature refers optical frequencies these are almost always frequencies in the infrared, which is below the visible spectrum. In 2009 a group of researchers announced cloaking at optical frequencies. In this case the cloaking frequency was centered at 1500 nm or 1.5 micrometers – the infrared.
Sonic frequencies
A laboratory metamaterial device, applicable to ultra-sound waves was demonstrated in January 2011. It can be applied to sound wavelengths corresponding to frequencies from 40 to 80 kHz.
The metamaterial acoustic cloak is designed to hide objects submerged in water. The metamaterial cloaking mechanism bends and twists sound waves by intentional design.
The cloaking mechanism consists of 16 concentric rings in a cylindrical configuration. Each ring has acoustic circuits. It is intentionally designed to guide sound waves in two dimensions.
Each ring has a different index of refraction. This causes sound waves to vary their speed from ring to ring. "The sound waves propagate around the outer ring, guided by the channels in the circuits, which bend the waves to wrap them around the outer layers of the cloak". It forms an array of cavities that slow the speed of the propagating sound waves. An experimental cylinder was submerged and then disappeared from sonar. Other objects of various shape and density were also hidden from the sonar. The acoustic cloak demonstrated effectiveness for frequencies of 40 kHz to 80 kHz.
In 2014 researchers created a 3D acoustic cloak from stacked plastic sheets dotted with repeating patterns of holes. The pyramidal geometry of the stack and the hole placement provide the effect.
Invisibility in diffusive light scattering media
In 2014, scientists demonstrated good cloaking performance in murky water, demonstrating that an object shrouded in fog can disappear completely when appropriately coated with metamaterial. This is due to the random scattering of light, such as that which occurs in clouds, fog, milk, frosted glass, etc., combined with the properties of the metatmaterial coating. When light is diffused, a thin coat of metamaterial around an object can make it essentially invisible under a range of lighting conditions.
Cloaking attempts
Broadband ground-plane cloak
If a transformation to quasi-orthogonal coordinates is applied to Maxwell's equations in order to conceal a perturbation on a flat conducting plane rather than a singular point, as in the first demonstration of a transformation optics-based cloak, then an object can be hidden underneath the perturbation. This is sometimes referred to as a "carpet" cloak.
As noted above, the original cloak demonstrated utilized resonant metamaterial elements to meet the effective material constraints. Utilizing a quasi-conformal transformation in this case, rather than the non-conformal original transformation, changed the required material properties. Unlike the original (singular expansion) cloak, the "carpet" cloak required less extreme material values. The quasi-conformal carpet cloak required anisotropic, inhomogeneous materials which only varied in permittivity. Moreover, the permittivity was always positive. This allowed the use of non-resonant metamaterial elements to create the cloak, significantly increasing the bandwidth.
An automated process, guided by a set of algorithms, was used to construct a metamaterial consisting of thousands of elements, each with its own geometry. Developing the algorithm allowed the manufacturing process to be automated, which resulted in fabrication of the metamaterial in nine days. The previous device used in 2006 was rudimentary in comparison, and the manufacturing process required four months in order to create the device. These differences are largely due to the different form of transformation: the original 2006 cloak transformed a singular point, while the ground-plane version transforms a plane, and the transformation in the carpet cloak was quasi-conformal, rather than non-conformal.
Other theories of cloaking
Other theories of cloaking discuss various science and research based theories for producing an electromagnetic cloak of invisibility. Theories presented employ transformation optics, event cloaking, dipolar scattering cancellation, tunneling light transmittance, sensors and active sources, and acoustic cloaking.
Institutional research
The research in the field of metamaterials has diffused out into the American government science research departments, including the US Naval Air Systems Command, US Air Force, and US Army. Many scientific institutions are involved including:
- California Institute of Technology
- Massachusetts Institute of Technology
- Colorado State University
- Pennsylvania State University
- Duke University
- Harvard University
- Aalto University
- Imperial College London
- Max Planck Society
- MSU Faculty of Physics
- National Institute of Standards and Technology
- Nederlandse Organisatie voor Wetenschappelijk Onderzoek
- University College London
- University of California, Berkeley
- University of California, Irvine
- University of California, Los Angeles
- University of California, San Diego
- University of Colorado
- University of Delaware
- University of Rochester
Funding for research into this technology is provided by the following American agencies:
- Air Force Research Laboratory
- Defense Advanced Research Projects Agency
- Director of Central Intelligence
- National Geospatial-Intelligence Agency
- Naval Air Systems Command
- Office of Naval Research
Through this research, it has been realized that developing a method for controlling electromagnetic fields can be applied to escape detection by radiated probing, or sonar technology, and to improve communications in the microwave range; that this method is relevant to superlens design and to the cloaking of objects within and from electromagnetic fields.
In the news
On October 20, 2006, the day after Duke University achieved enveloping and "disappearing" an object in the microwave range, the story was reported by Associated Press. Media outlets covering the story included USA Today, MSNBC's Countdown With Keith Olbermann: Sight Unseen, The New York Times with Cloaking Copper, Scientists Take Step Toward Invisibility, (London) The Times with Don't Look Now—Visible Gains in the Quest for Invisibility, Christian Science Monitor with Disappear Into Thin Air? Scientists Take Step Toward Invisibility, Australian Broadcasting, Reuters with Invisibility Cloak a Step Closer, and the (Raleigh) News & Observer with 'Invisibility Cloak a Step Closer.
On November 6, 2006, the Duke University research and development team was selected as part of the Scientific American best 50 articles of 2006.
In the month of November 2009, "research into designing and building unique 'metamaterials' has received a £4.9 million funding boost. Metamaterials can be used for invisibility 'cloaking' devices, sensitive security sensors that can detect tiny quantities of dangerous substances, and flat lenses that can be used to image tiny objects much smaller than the wavelength of light."
In November 2010, scientists at the University of St Andrews in Scotland reported the creation of a flexible cloaking material they call "Metaflex", which may bring industrial applications significantly closer.
In 2014, the world 's first 3D acoustic device was built by Duke engineers.