Nuclear binding energy

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Nuclear_binding_energy

Nuclear binding energy in experimental physics is the minimum energy that is required to disassemble the nucleus of an atom into its constituent protons and neutrons, known collectively as nucleons. The binding energy for stable nuclei is always a positive number, as the nucleus must gain energy for the nucleons to move apart from each other. Nucleons are attracted to each other by the strong nuclear force. In theoretical nuclear physics, the nuclear binding energy is considered a negative number. In this context it represents the energy of the nucleus relative to the energy of the constituent nucleons when they are infinitely far apart. Both the experimental and theoretical views are equivalent, with slightly different emphasis on what the binding energy means.

The mass of an atomic nucleus is less than the sum of the individual masses of the free constituent protons and neutrons. The difference in mass can be calculated by the Einstein equation, E = mc², where E is the nuclear binding energy, c is the speed of light, and m is the difference in mass. This 'missing mass' is known as the mass defect, and represents the energy that was released when the nucleus was formed.

The term "nuclear binding energy" may also refer to the energy balance in processes in which the nucleus splits into fragments composed of more than one nucleon. If new binding energy is available when light nuclei fuse (nuclear fusion), or when heavy nuclei split (nuclear fission), either process can result in release of this binding energy. This energy may be made available as nuclear energy and can be used to produce electricity, as in nuclear power, or in a nuclear weapon. When a large nucleus splits into pieces, excess energy is emitted as gamma rays and the kinetic energy of various ejected particles (nuclear fission products).

These nuclear binding energies and forces are on the order of one million times greater than the electron binding energies of light atoms like hydrogen.

Introduction

Nuclear energy

An absorption or release of nuclear energy occurs in nuclear reactions or radioactive decay; those that absorb energy are called endothermic reactions and those that release energy are exothermic reactions. Energy is consumed or released because of differences in the nuclear binding energy between the incoming and outgoing products of the nuclear transmutation.

The best-known classes of exothermic nuclear transmutations are nuclear fission and nuclear fusion. Nuclear energy may be released by fission, when heavy atomic nuclei (like uranium and plutonium) are broken apart into lighter nuclei. The energy from fission is used to generate electric power in hundreds of locations worldwide. Nuclear energy is also released during fusion, when light nuclei like hydrogen are combined to form heavier nuclei such as helium. The Sun and other stars use nuclear fusion to generate thermal energy which is later radiated from the surface, a type of stellar nucleosynthesis. In any exothermic nuclear process, nuclear mass might ultimately be converted to thermal energy, emitted as heat.

In order to quantify the energy released or absorbed in any nuclear transmutation, one must know the nuclear binding energies of the nuclear components involved in the transmutation.

The nuclear force

Electrons and nuclei are kept together by electrostatic attraction (negative attracts positive). Furthermore, electrons are sometimes shared by neighboring atoms or transferred to them (by processes of quantum physics); this link between atoms is referred to as a chemical bond and is responsible for the formation of all chemical compounds.

The electric force does not hold nuclei together, because all protons carry a positive charge and repel each other. If two protons were touching, their repulsion force would be almost 40 Newton. Because each of the neutrons carries total charge zero, a proton could electrically attract a neutron if the proton could induce the neutron to become electrically polarized. However, having the neutron between two protons (so their mutual repulsion decreases to 10 N) would attract the neutron only for an electric quadrupole (− + + −) arrangement. Higher multipoles, needed to satisfy more protons, cause weaker attraction, and quickly become implausible.

After the proton and neutron magnetic moments were measured and verified, it was apparent that their magnetic forces might be 20 or 30 newtons, attractive if properly oriented. A pair of protons would do 10⁻¹³ joules of work to each other as they approach – that is, they would need to release energy of 0.5 MeV in order to stick together. On the other hand, once a pair of nucleons magnetically stick, their external fields are greatly reduced, so it is difficult for many nucleons to accumulate much magnetic energy.

Therefore, another force, called the nuclear force (or residual strong force) holds the nucleons of nuclei together. This force is a residuum of the strong interaction, which binds quarks into nucleons at an even smaller level of distance.

The fact that nuclei do not clump together (fuse) under normal conditions suggests that the nuclear force must be weaker than the electric repulsion at larger distances, but stronger at close range. Therefore, it has short-range characteristics. An analogy to the nuclear force is the force between two small magnets: magnets are very difficult to separate when stuck together, but once pulled a short distance apart, the force between them drops almost to zero.

Unlike gravity or electrical forces, the nuclear force is effective only at very short distances. At greater distances, the electrostatic force dominates: the protons repel each other because they are positively charged, and like charges repel. For that reason, the protons forming the nuclei of ordinary hydrogen—for instance, in a balloon filled with hydrogen—do not combine to form helium (a process that also would require some protons to combine with electrons and become neutrons). They cannot get close enough for the nuclear force, which attracts them to each other, to become important. Only under conditions of extreme pressure and temperature (for example, within the core of a star), can such a process take place.

Physics of nuclei

Main article: Atomic nucleus

There are around 94 naturally occurring elements on earth. The atoms of each element have a nucleus containing a specific number of protons (always the same number for a given element), and some number of neutrons, which is often roughly a similar number. Two atoms of the same element having different numbers of neutrons are known as isotopes of the element. Different isotopes may have different properties – for example one might be stable and another might be unstable, and gradually undergo radioactive decay to become another element.

The hydrogen nucleus contains just one proton. Its isotope deuterium, or heavy hydrogen, contains a proton and a neutron. Helium contains two protons and two neutrons, and carbon, nitrogen and oxygen – six, seven and eight of each particle, respectively. However, a helium nucleus weighs less than the sum of the weights of the two heavy hydrogen nuclei which combine to make it. The same is true for carbon, nitrogen and oxygen. For example, the carbon nucleus is slightly lighter than three helium nuclei, which can combine to make a carbon nucleus. This difference is known as the mass defect.

Mass defect

Not to be confused with mass excess in nuclear physics or mass defect in mass spectrometry.

Mass defect (also called "mass deficit") is the difference between the mass of an object and the sum of the masses of its constituent particles. Discovered by Albert Einstein in 1905, it can be explained using his formula E = mc², which describes the equivalence of energy and mass. The decrease in mass is equal to the energy emitted in the reaction of an atom's creation divided by c². By this formula, adding energy also increases mass (both weight and inertia), whereas removing energy decreases mass. For example, a helium atom containing four nucleons has a mass about 0.8% less than the total mass of four hydrogen atoms (each containing one nucleon). The helium nucleus has four nucleons bound together, and the binding energy which holds them together is, in effect, the missing 0.8% of mass.

If a combination of particles contains extra energy—for instance, in a molecule of the explosive TNT—weighing it reveals some extra mass, compared to its end products after an explosion. (The end products must be weighed after they have been stopped and cooled, however, as the extra mass must escape from the system as heat before its loss can be noticed, in theory.) On the other hand, if one must inject energy to separate a system of particles into its components, then the initial mass is less than that of the components after they are separated. In the latter case, the energy injected is "stored" as potential energy, which shows as the increased mass of the components that store it. This is an example of the fact that energy of all types is seen in systems as mass, since mass and energy are equivalent, and each is a "property" of the other.

The latter scenario is the case with nuclei such as helium: to break them up into protons and neutrons, one must inject energy. On the other hand, if a process existed going in the opposite direction, by which hydrogen atoms could be combined to form helium, then energy would be released. The energy can be computed using E = Δmc² for each nucleus, where Δm is the difference between the mass of the helium nucleus and the mass of four protons (plus two electrons, absorbed to create the neutrons of helium).

For lighter elements, the energy that can be released by assembling them from lighter elements decreases, and energy can be released when they fuse. This is true for nuclei lighter than iron/nickel. For heavier nuclei, more energy is needed to bind them, and that energy may be released by breaking them up into fragments (known as nuclear fission). Nuclear power is generated at present by breaking up uranium nuclei in nuclear power reactors, and capturing the released energy as heat, which is converted to electricity.

As a rule, very light elements can fuse comparatively easily, and very heavy elements can break up via fission very easily; elements in the middle are more stable and it is difficult to make them undergo either fusion or fission in an environment such as a laboratory.

The reason the trend reverses after iron is the growing positive charge of the nuclei, which tends to force nuclei to break up. It is resisted by the strong nuclear interaction, which holds nucleons together. The electric force may be weaker than the strong nuclear force, but the strong force has a much more limited range: in an iron nucleus, each proton repels the other 25 protons, while the nuclear force only binds close neighbors. So for larger nuclei, the electrostatic forces tend to dominate and the nucleus will tend over time to break up.

As nuclei grow bigger still, this disruptive effect becomes steadily more significant. By the time polonium is reached (84 protons), nuclei can no longer accommodate their large positive charge, but emit their excess protons quite rapidly in the process of alpha radioactivity—the emission of helium nuclei, each containing two protons and two neutrons. (Helium nuclei are an especially stable combination.) Because of this process, nuclei with more than 94 protons are not found naturally on Earth (see periodic table). The isotopes beyond uranium (atomic number 92) with the longest half-lives are plutonium-244 (80 million years) and curium-247 (16 million years).

Nuclear reactions in the sun

The nuclear fusion process works as follows: five billion years ago, the new Sun formed when gravity pulled together a vast cloud of hydrogen and dust, from which the Earth and other planets also arose. The gravitational pull released energy and heated the early Sun, much in the way Helmholtz proposed.

Thermal energy appears as the motion of atoms and molecules: the higher the temperature of a collection of particles, the greater is their velocity and the more violent are their collisions. When the temperature at the center of the newly formed Sun became great enough for collisions between hydrogen nuclei to overcome their electric repulsion, and bring them into the short range of the attractive nuclear force, nuclei began to stick together. When this began to happen, protons combined into deuterium and then helium, with some protons changing in the process to neutrons (plus positrons, positive electrons, which combine with electrons and annihilate into gamma-ray photons). This released nuclear energy now keeps up the high temperature of the Sun's core, and the heat also keeps the gas pressure high, keeping the Sun at its present size, and stopping gravity from compressing it any more. There is now a stable balance between gravity and pressure.

Different nuclear reactions may predominate at different stages of the Sun's existence, including the proton–proton reaction and the carbon–nitrogen cycle—which involves heavier nuclei, but whose final product is still the combination of protons to form helium.

A branch of physics, the study of controlled nuclear fusion, has tried since the 1950s to derive useful power from nuclear fusion reactions that combine small nuclei into bigger ones, typically to heat boilers, whose steam could turn turbines and produce electricity. No earthly laboratory can match one feature of the solar powerhouse: the great mass of the Sun, whose weight keeps the hot plasma compressed and confines the nuclear furnace to the Sun's core. Instead, physicists use strong magnetic fields to confine the plasma, and for fuel they use heavy forms of hydrogen, which burn more easily. Magnetic traps can be rather unstable, and any plasma hot enough and dense enough to undergo nuclear fusion tends to slip out of them after a short time. Even with ingenious tricks, the confinement in most cases lasts only a small fraction of a second. Exciton binding energy has been predicted to be key for efficient solar cells due to recent studies.

Combining nuclei

Small nuclei that are larger than hydrogen can combine into bigger ones and release energy, but in combining such nuclei, the amount of energy released is much smaller compared to hydrogen fusion. The reason is that while the overall process releases energy from letting the nuclear attraction do its work, energy must first be injected to force together positively charged protons, which also repel each other with their electric charge.

For elements that weigh more than iron (a nucleus with 26 protons), the fusion process no longer releases energy. In even heavier nuclei energy is consumed, not released, by combining similarly sized nuclei. With such large nuclei, overcoming the electric repulsion (which affects all protons in the nucleus) requires more energy than is released by the nuclear attraction (which is effective mainly between close neighbors). Conversely, energy could actually be released by breaking apart nuclei heavier than iron.

With the nuclei of elements heavier than lead, the electric repulsion is so strong that some of them spontaneously eject positive fragments, usually nuclei of helium that form stable (alpha particles). This spontaneous break-up is one of the forms of radioactivity exhibited by some nuclei.

Nuclei heavier than lead (except for bismuth, thorium, and uranium) spontaneously break up too quickly to appear in nature as primordial elements, though they can be produced artificially or as intermediates in the decay chains of heavier elements. Generally, the heavier the nuclei are, the faster they spontaneously decay.

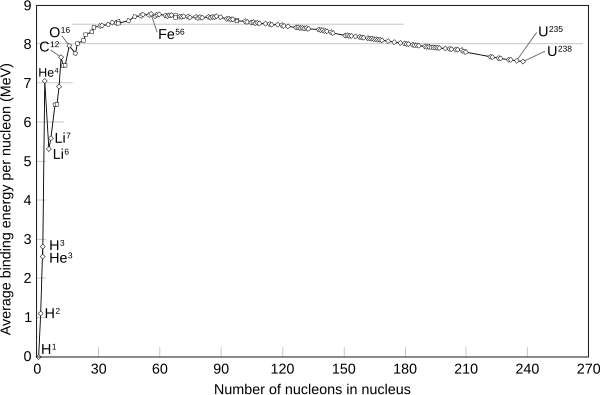
Iron nuclei are the most stable nuclei (in particular iron-56), and the best sources of energy are therefore nuclei whose weights are as far removed from iron as possible. One can combine the lightest ones—nuclei of hydrogen (protons)—to form nuclei of helium, and that is how the Sun generates its energy. Alternatively, one can break up the heaviest ones—nuclei of uranium or plutonium—into smaller fragments, and that is what nuclear reactors do.

Nuclear binding energy

An example that illustrates nuclear binding energy is the nucleus of ¹²C (carbon-12), which contains 6 protons and 6 neutrons. The protons are all positively charged and repel each other, but the nuclear force overcomes the repulsion and causes them to stick together. The nuclear force is a close-range force (it is strongly attractive at a distance of 1.0 fm and becomes extremely small beyond a distance of 2.5 fm), and virtually no effect of this force is observed outside the nucleus. The nuclear force also pulls neutrons together, or neutrons and protons.

The energy of the nucleus is negative with regard to the energy of the particles pulled apart to infinite distance (just like the gravitational energy of planets of the solar system), because energy must be utilized to split a nucleus into its individual protons and neutrons. Mass spectrometers have measured the masses of nuclei, which are always less than the sum of the masses of protons and neutrons that form them, and the difference—by the formula E = mc²—gives the binding energy of the nucleus.

Nuclear fusion

The binding energy of helium is the energy source of the Sun and of most stars. The sun is composed of 74 percent hydrogen (measured by mass), an element having a nucleus consisting of a single proton. Energy is released in the sun when 4 protons combine into a helium nucleus, a process in which two of them are also converted to neutrons.

The conversion of protons to neutrons is the result of another nuclear force, known as the weak (nuclear) force. The weak force, like the strong force, has a short range, but is much weaker than the strong force. The weak force tries to make the number of neutrons and protons into the most energetically stable configuration. For nuclei containing less than 40 particles, these numbers are usually about equal. Protons and neutrons are closely related and are collectively known as nucleons. As the number of particles increases toward a maximum of about 209, the number of neutrons to maintain stability begins to outstrip the number of protons, until the ratio of neutrons to protons is about three to two.

The protons of hydrogen combine to helium only if they have enough velocity to overcome each other's mutual repulsion sufficiently to get within range of the strong nuclear attraction. This means that fusion only occurs within a very hot gas. Hydrogen hot enough for combining to helium requires an enormous pressure to keep it confined, but suitable conditions exist in the central regions of the Sun, where such pressure is provided by the enormous weight of the layers above the core, pressed inwards by the Sun's strong gravity. The process of combining protons to form helium is an example of nuclear fusion.

Producing helium from normal hydrogen would be practically impossible on earth because of the difficulty in creating deuterium. Research is being undertaken on developing a process using deuterium and tritium. The earth's oceans contain a large amount of deuterium that could be used and tritium can be made in the reactor itself from lithium, and furthermore the helium product does not harm the environment, so some consider nuclear fusion a good alternative to supply our energy needs. Experiments to carry out this form of fusion have so far only partially succeeded. Sufficiently hot deuterium and tritium must be confined. One technique is to use very strong magnetic fields, because charged particles (like those trapped in the Earth's radiation belt) are guided by magnetic field lines.

The binding energy maximum and ways to approach it by decay

In the main isotopes of light elements, such as carbon, nitrogen and oxygen, the most stable combination of neutrons and of protons are when the numbers are equal (this continues to element 20, calcium). However, in heavier nuclei, the disruptive energy of protons increases, since they are confined to a tiny volume and repel each other. The energy of the strong force holding the nucleus together also increases, but at a slower rate, as if inside the nucleus, only nucleons close to each other are tightly bound, not ones more widely separated.

The net binding energy of a nucleus is that of the nuclear attraction, minus the disruptive energy of the electric force. As nuclei get heavier than helium, their net binding energy per nucleon (deduced from the difference in mass between the nucleus and the sum of masses of component nucleons) grows more and more slowly, reaching its peak at iron. As nucleons are added, the total nuclear binding energy always increases—but the total disruptive energy of electric forces (positive protons repelling other protons) also increases, and past iron, the second increase outweighs the first. Iron-56 (⁵⁶Fe) is the most efficiently bound nucleus meaning that it has the least average mass per nucleon. However, nickel-62 is the most tightly bound nucleus in terms of binding energy per nucleon. (Nickel-62's higher binding energy does not translate to a larger mean mass loss than ⁵⁶Fe, because ⁶²Ni has a slightly higher ratio of neutrons/protons than does iron-56, and the presence of the heavier neutrons increases nickel-62's average mass per nucleon).

To reduce the disruptive energy, the weak interaction allows the number of neutrons to exceed that of protons—for instance, the main isotope of iron has 26 protons and 30 neutrons. Isotopes also exist where the number of neutrons differs from the most stable number for that number of nucleons. If changing one proton into a neutron or one neutron into a proton increases the stability (lowering the mass), then this will happen through beta decay, meaning the nuclide will be radioactive.

The two methods for this conversion are mediated by the weak force, and involve types of beta decay. In the simplest beta decay, neutrons are converted to protons by emitting a negative electron and an antineutrino. This is always possible outside a nucleus because neutrons are more massive than protons by an equivalent of about 2.5 electrons. In the opposite process, which only happens within a nucleus, and not to free particles, a proton may become a neutron by ejecting a positron and an electron neutrino. This is permitted if enough energy is available between parent and daughter nuclides to do this (the required energy difference is equal to 1.022 MeV, which is the mass of 2 electrons). If the mass difference between parent and daughter is less than this, a proton-rich nucleus may still convert protons to neutrons by the process of electron capture, in which a proton simply electron captures one of the atom's K orbital electrons, emits a neutrino, and becomes a neutron.

Among the heaviest nuclei, starting with tellurium nuclei (element 52) containing 104 or more nucleons, electric forces may be so destabilizing that entire chunks of the nucleus may be ejected, usually as alpha particles, which consist of two protons and two neutrons (alpha particles are fast helium nuclei). (Beryllium-8 also decays, very quickly, into two alpha particles.) This type of decay becomes more and more probable as elements rise in atomic weight past 104.

The curve of binding energy is a graph that plots the binding energy per nucleon against atomic mass. This curve has its main peak at iron and nickel and then slowly decreases again, and also a narrow isolated peak at helium, which is more stable than other low-mass nuclides. The heaviest nuclei in more than trace quantities in nature, uranium ²³⁸U, are unstable, but having a half-life of 4.5 billion years, close to the age of the Earth, they are still relatively abundant; they (and other nuclei heavier than helium) have formed in stellar evolution events like supernova explosions preceding the formation of the solar system. The most common isotope of thorium, ²³²Th, also undergoes alpha particle emission, and its half-life (time over which half a number of atoms decays) is even longer, by several times. In each of these, radioactive decay produces daughter isotopes that are also unstable, starting a chain of decays that ends in some stable isotope of lead.

Calculation of nuclear binding energy

Calculation can be employed to determine the nuclear binding energy of nuclei. The calculation involves determining the mass defect, converting it into energy, and expressing the result as energy per mole of atoms, or as energy per nucleon.

Conversion of mass defect into energy

Mass defect is defined as the difference between the mass of a nucleus, and the sum of the masses of the nucleons of which it is composed. The mass defect is determined by calculating three quantities. These are: the actual mass of the nucleus, the composition of the nucleus (number of protons and of neutrons), and the masses of a proton and of a neutron. This is then followed by converting the mass defect into energy. This quantity is the nuclear binding energy, however it must be expressed as energy per mole of atoms or as energy per nucleon.

Fission and fusion

Nuclear energy is released by the splitting (fission) or merging (fusion) of the nuclei of atom(s). The conversion of nuclear mass–energy to a form of energy, which can remove some mass when the energy is removed, is consistent with the mass–energy equivalence formula:

ΔE = Δm c²,

where

ΔE = energy release,

Δm = mass defect,

and c = the speed of light in a vacuum.

Nuclear energy was first discovered by French physicist Henri Becquerel in 1896, when he found that photographic plates stored in the dark near uranium were blackened like X-ray plates (X-rays had recently been discovered in 1895).

Nickel-62 has the highest binding energy per nucleon of any isotope. If an atom of lower average binding energy per nucleon is changed into two atoms of higher average binding energy per nucleon, energy is emitted. (The average here is the weighted average.) Also, if two atoms of lower average binding energy fuse into an atom of higher average binding energy, energy is emitted. The chart shows that fusion, or combining, of hydrogen nuclei to form heavier atoms releases energy, as does fission of uranium, the breaking up of a larger nucleus into smaller parts.

Nuclear energy is released by three exoenergetic (or exothermic) processes:

• Radioactive decay, where a neutron or proton in the radioactive nucleus decays spontaneously by emitting either particles, electromagnetic radiation (gamma rays), or both. Note that for radioactive decay, it is not strictly necessary for the binding energy to increase. What is strictly necessary is that the mass decrease. If a neutron turns into a proton and the energy of the decay is less than 0.782343 MeV, the difference between the masses of the neutron and proton multiplied by the speed of light squared, (such as rubidium-87 decaying to strontium-87), the average binding energy per nucleon will actually decrease.
• Fusion, two atomic nuclei fuse together to form a heavier nucleus
• Fission, the breaking of a heavy nucleus into two (or more rarely three) lighter nuclei, and some neutrons

The energy producing nuclear interaction of light elements requires some clarification. Frequently, all light element energy-producing nuclear interactions are classified as fusion, however by the given definition above fusion requires that the products include a nucleus that is heavier than the reactants. Light elements can experience energy producing nuclear interactions by fusion or fission. All energy producing nuclear interactions between two Hydrogen isotopes and between hydrogen and helium-3 are fusion as the product of these interactions include a heavier nucleus. However, the energy producing nuclear interaction of a neutron with Lithium–6 produces Hydrogen-3 and Helium-4, each a lighter nucleus. By the definition above, this nuclear interaction is fission, not fusion. When fission is caused by a neutron, as in this case, it is called induced fission.

Light element energy-producing nuclear interactions:

Fusion

¹H + ¹H → ²H  Q ≈ 1.44 MeV

¹H + ²H → ³He  Q ≈ 5.52 MeV

²H + ²H → ³H + p⁺  Q ≈ 4.08 MeV

²H + ²H → ³He + n  Q ≈ 3.27 MeV

²H + ³H → ⁴He + n  Q ≈ 17.53 MeV

²H + ³He → ⁴He + p⁺  Q ≈ 18.34 MeV

³He + ³He → ⁴He + p⁺ + p⁺  Q ≈ 12.85 MeV

³He + ⁶Li → ⁴He + ⁴He + p⁺  Q ≈ 22.36 MeV

Fission

⁶Li + p⁺ → ⁴He + ³He  Q ≈ 4.02 MeV

⁶Li + ²H → ⁴He + ⁴He  Q ≈ 11.18 MeV

⁶Li + ³He → ⁴He + ⁴He + p⁺  Q ≈ 0.94 MeV

⁷Li + p⁺ → ⁴He + ⁴He  Q ≈ 17.34 MeV

⁷Li + ²H → ⁴He + ⁴He + n  Q ≈ 15.11 MeV

¹¹B + p⁺ → ⁴He + ⁴He + ⁴He  Q ≈ 8.68 MeV

Binding energy for atoms

The binding energy of an atom (including its electrons) is not exactly the same as the binding energy of the atom's nucleus. The measured mass deficits of isotopes are always listed as mass deficits of the neutral atoms of that isotope, and mostly in MeV/c². As a consequence, the listed mass deficits are not a measure of the stability or binding energy of isolated nuclei, but for the whole atoms. There is a very practical reason for this, namely that it is very hard to totally ionize heavy elements, i.e. strip them of all of their electrons.

This practice is useful for other reasons, too: stripping all the electrons from a heavy unstable nucleus (thus producing a bare nucleus) changes the lifetime of the nucleus, or the nucleus of a stable neutral atom can likewise become unstable after stripping, indicating that the nucleus cannot be treated independently. Examples of this have been shown in bound-state β decay experiments performed at the GSI heavy ion accelerator. This is also evident from phenomena like electron capture. Theoretically, in orbital models of heavy atoms, the electron orbits partially inside the nucleus (it does not orbit in a strict sense, but has a non-vanishing probability of being located inside the nucleus).

A nuclear decay happens to the nucleus, meaning that properties ascribed to the nucleus change in the event. In the field of physics the concept of "mass deficit" as a measure for "binding energy" means "mass deficit of the neutral atom" (not just the nucleus) and is a measure for stability of the whole atom.

Nuclear binding energy curve

Binding energy per nucleon for a selection of nuclides. The nuclide with the highest value, ⁶²Ni, does not appear. The horizontal lines are at 8 and 8.5 MeV.

In the periodic table of elements, the series of light elements from hydrogen up to sodium is observed to exhibit generally increasing binding energy per nucleon as the atomic mass increases. This increase is generated by increasing forces per nucleon in the nucleus, as each additional nucleon is attracted by other nearby nucleons, and thus more tightly bound to the whole. Helium-4 and oxygen-16 are particularly stable exceptions to the trend (see figure on the right). This is because they are doubly magic, meaning their protons and neutrons both fill their respective nuclear shells.

The region of increasing binding energy is followed by a region of relative stability (saturation) in the sequence from about mass 30 through about mass 90. In this region, the nucleus has become large enough that nuclear forces no longer completely extend efficiently across its width. Attractive nuclear forces in this region, as atomic mass increases, are nearly balanced by repellent electromagnetic forces between protons, as the atomic number increases.

Finally, in the heavier elements, there is a gradual decrease in binding energy per nucleon as atomic number increases. In this region of nuclear size, electromagnetic repulsive forces are beginning to overcome the strong nuclear force attraction.

At the peak of binding energy, nickel-62 is the most tightly bound nucleus (per nucleon), followed by iron-58 and iron-56. This is the approximate basic reason why iron and nickel are very common metals in planetary cores, since they are produced profusely as end products in supernovae and in the final stages of silicon burning in stars. However, it is not binding energy per defined nucleon (as defined above), which controls exactly which nuclei are made, because within stars, neutrons and protons can inter-convert to release even more energy per generic nucleon. In fact, it has been argued that photodisintegration of ⁶²Ni to form ⁵⁶Fe may be energetically possible in an extremely hot star core, due to this beta decay conversion of neutrons to protons. This favors the creation of ⁵⁶Fe, the nuclide with the lowest mass per nucleon. However, at high temperatures not all matter will be in the lowest energy state. This energetic maximum should also hold for ambient conditions, say T = 298 K and p = 1 atm, for neutral condensed matter consisting of ⁵⁶Fe atoms—however, in these conditions nuclei of atoms are inhibited from fusing into the most stable and low energy state of matter.

Elements with high binding energy per nucleon, like iron and nickel, cannot undergo fission, but they can theoretically undergo fusion with hydrogen, deuterium, helium, and carbon, for instance:

⁶²Ni + ¹²C → ⁷⁴Se  Q = 5.467 MeV

It is generally believed that iron-56 is more common than nickel isotopes in the universe for mechanistic reasons, because its unstable progenitor nickel-56 is copiously made by staged build-up of 14 helium nuclei inside supernovas, where it has no time to decay to iron before being released into the interstellar medium in a matter of a few minutes, as the supernova explodes. However, nickel-56 then decays to cobalt-56 within a few weeks, then this radioisotope finally decays to iron-56 with a half life of about 77.3 days. The radioactive decay-powered light curve of such a process has been observed to happen in type II supernovae, such as SN 1987A. In a star, there are no good ways to create nickel-62 by alpha-addition processes, or else there would presumably be more of this highly stable nuclide in the universe.

Binding energy and nuclide masses

The fact that the maximum binding energy is found in medium-sized nuclei is a consequence of the trade-off in the effects of two opposing forces that have different range characteristics. The attractive nuclear force (strong nuclear force), which binds protons and neutrons equally to each other, has a limited range due to a rapid exponential decrease in this force with distance. However, the repelling electromagnetic force, which acts between protons to force nuclei apart, falls off with distance much more slowly (as the inverse square of distance). For nuclei larger than about four nucleons in diameter, the additional repelling force of additional protons more than offsets any binding energy that results between further added nucleons as a result of additional strong force interactions. Such nuclei become increasingly less tightly bound as their size increases, though most of them are still stable. Finally, nuclei containing more than 209 nucleons (larger than about 6 nucleons in diameter) are all too large to be stable, and are subject to spontaneous decay to smaller nuclei.

Nuclear fusion produces energy by combining the very lightest elements into more tightly bound elements (such as hydrogen into helium), and nuclear fission produces energy by splitting the heaviest elements (such as uranium and plutonium) into more tightly bound elements (such as barium and krypton). The nuclear fission of a few light elements (such as Lithium) occurs because Helium-4 is a product and a more tightly bound element than slightly heavier elements. Both processes produce energy as the sum of the masses of the products is less than the sum of the masses of the reacting nuclei.

As seen above in the example of deuterium, nuclear binding energies are large enough that they may be easily measured as fractional mass deficits, according to the equivalence of mass and energy. The atomic binding energy is simply the amount of energy (and mass) released, when a collection of free nucleons are joined together to form a nucleus.

Nuclear binding energy can be computed from the difference in mass of a nucleus, and the sum of the masses of the number of free neutrons and protons that make up the nucleus. Once this mass difference, called the mass defect or mass deficiency, is known, Einstein's mass–energy equivalence formula E = mc² can be used to compute the binding energy of any nucleus. Early nuclear physicists used to refer to computing this value as a "packing fraction" calculation.

For example, the dalton (1 Da) is defined as 1/12 of the mass of a ¹²C atom—but the atomic mass of a ¹H atom (which is a proton plus electron) is 1.007825 Da, so each nucleon in ¹²C has lost, on average, about 0.8% of its mass in the form of binding energy.

Semiempirical formula for nuclear binding energy

Main article: Semi-empirical mass formula

For a nucleus with A nucleons, including Z protons and N neutrons, a semi-empirical formula for the binding energy (E_B) per nucleon is:

$${\displaystyle \frac{E_{\text{B}}}{A\cdot \text{MeV}}=a-\frac{b}{A^{1/3}}-\frac{c{Z}^2}{A^{4/3}}-\frac{d{\left(N-Z\right)}^2}{A^2}\pm \frac{e}{A^{7/4}}}$$

where the coefficients are given by: ${\displaystyle a=14.0}$; ${\displaystyle b=13.0}$; ${\displaystyle c=0.585}$; ${\displaystyle d=19.3}$; ${\displaystyle e=33}$.

The first term ${\displaystyle a}$ is called the saturation contribution and ensures that the binding energy per nucleon is the same for all nuclei to a first approximation. The term ${\displaystyle -b/A^{1/3}}$ is a surface tension effect and is proportional to the number of nucleons that are situated on the nuclear surface; it is largest for light nuclei. The term ${\displaystyle -c{Z}^2/A^{4/3}}$ is the Coulomb electrostatic repulsion; this becomes more important as ${\displaystyle Z}$ increases. The symmetry correction term ${\displaystyle -d(N-Z{)}^2/A^2}$ takes into account the fact that in the absence of other effects the most stable arrangement has equal numbers of protons and neutrons; this is because the n–p interaction in a nucleus is stronger than either the n−n or p−p interaction. The pairing term ${\displaystyle \pm e/A^{7/4}}$ is purely empirical; it is + for even–even nuclei and − for odd–odd nuclei. When A is odd, the pairing term is identically zero.

A graphical representation of the semi-empirical binding energy formula. The binding energy per nucleon in MeV (highest numbers in yellow, in excess of 8.5 MeV per nucleon) is plotted for various nuclides as a function of Z, the atomic number (y-axis), vs. N, the number of neutrons (x-axis). The highest numbers are seen for Z = 26 (iron).

Example values deduced from experimentally measured atom nuclide masses

The following table lists some binding energies and mass defect values. Notice also that we use 1 Da = 931.494028(23) MeV/c². To calculate the binding energy we use the formula Z (m_p + m_e) + N m_n − m_nuclide where Z denotes the number of protons in the nuclides and N their number of neutrons. We take m_p = 938.2720813(58) MeV/c², m_e = 0.5109989461(30) MeV/c² and m_n = 939.5654133(58) MeV/c². The letter A denotes the sum of Z and N (number of nucleons in the nuclide). If we assume the reference nucleon has the mass of a neutron (so that all "total" binding energies calculated are maximal) we could define the total binding energy as the difference from the mass of the nucleus, and the mass of a collection of A free neutrons. In other words, it would be (Z + N) m_n − m_nuclide. The "total binding energy per nucleon" would be this value divided by A.

Most strongly bound nuclides atoms

nuclide	Z	N	mass excess	total mass	total mass / A	total binding energy / A	mass defect	binding energy	binding energy / A
56Fe	26	30	−60.6054 MeV	55.934937 Da	0.9988372 Da	9.1538 MeV	0.528479 Da	492.275 MeV	8.7906 MeV
58Fe	26	32	−62.1534 MeV	57.932276 Da	0.9988496 Da	9.1432 MeV	0.547471 Da	509.966 MeV	8.7925 MeV
60Ni	28	32	−64.472 MeV	59.93079 Da	0.9988464 Da	9.1462 MeV	0.565612 Da	526.864 MeV	8.7811 MeV
62Ni	28	34	−66.7461 MeV	61.928345 Da	0.9988443 Da	9.1481 MeV	0.585383 Da	545.281 MeV	8.7948 MeV

⁵⁶Fe has the lowest nucleon-specific mass of the four nuclides listed in this table, but this does not imply it is the strongest bound atom per hadron, unless the choice of beginning hadrons is completely free. Iron releases the largest energy if any 56 nucleons are allowed to build a nuclide—changing one to another if necessary, The highest binding energy per hadron, with the hadrons starting as the same number of protons Z and total nucleons A as in the bound nucleus, is ⁶²Ni. Thus, the true absolute value of the total binding energy of a nucleus depends on what we are allowed to construct the nucleus out of. If all nuclei of mass number A were to be allowed to be constructed of A neutrons, then ⁵⁶Fe would release the most energy per nucleon, since it has a larger fraction of protons than ⁶²Ni. However, if nuclei are required to be constructed of only the same number of protons and neutrons that they contain, then nickel-62 is the most tightly bound nucleus, per nucleon.

Some light nuclides resp. atoms

nuclide	Z	N	mass excess	total mass	total mass / A	total binding energy / A	mass defect	binding energy	binding energy / A
n	0	1	8.0716 MeV	1.008665 Da	1.008665 Da	0.0000 MeV	0 Da	0 MeV	0 MeV
1H	1	0	7.2890 MeV	1.007825 Da	1.007825 Da	0.7826 MeV	0.0000000146 Da	0.0000136 MeV	13.6 eV
2H	1	1	13.13572 MeV	2.014102 Da	1.007051 Da	1.50346 MeV	0.002388 Da	2.22452 MeV	1.11226 MeV
3H	1	2	14.9498 MeV	3.016049 Da	1.005350 Da	3.08815 MeV	0.0091058 Da	8.4820 MeV	2.8273 MeV
3He	2	1	14.9312 MeV	3.016029 Da	1.005343 Da	3.09433 MeV	0.0082857 Da	7.7181 MeV	2.5727 MeV

In the table above it can be seen that the decay of a neutron, as well as the transformation of tritium into helium-3, releases energy; hence, it manifests a stronger bound new state when measured against the mass of an equal number of neutrons (and also a lighter state per number of total hadrons). Such reactions are not driven by changes in binding energies as calculated from previously fixed N and Z numbers of neutrons and protons, but rather in decreases in the total mass of the nuclide/per nucleon, with the reaction. (Note that the Binding Energy given above for hydrogen-1 is the atomic binding energy, not the nuclear binding energy which would be zero.)

Persecution of Muslims during the Ottoman contraction

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Persecution_of_Muslims_during_the_Ottoman_contraction

During the decline and dissolution of the Ottoman Empire, Muslim (including Ottoman Turks, Albanians, Bosniaks, Circassians, Serb Muslims, Greek Muslims, Muslim Roma, Pomaks) inhabitants living in territories previously under Ottoman control, often found themselves as a persecuted minority after borders were re-drawn. These populations were subject to genocide, expropriation, massacres, and ethnic cleansing.

The 19th century saw the rise of nationalism in the Balkans coincident with the decline of Ottoman power, which resulted in the establishment of an independent Greece, Serbia and Bulgaria and Romania. At the same time, the Russian Empire expanded into previously Ottoman-ruled or Ottoman-allied regions of the Caucasus and the Black Sea region. These conflicts created large numbers of Muslim refugees. Persecutions of Muslims resumed during World War I by the invading Russian troops in the east and during the Turkish War of Independence in the west, east, and south of Anatolia by Greeks and Armenians. After the Greco-Turkish War, a population exchange between Greece and Turkey took place, and most Muslims of Greece left. During these times many Muslim refugees, called Muhacir, settled in Turkey.

Background

Turkish presence and Islamisation of native peoples in the Balkans

For the first time, Ottoman military expeditions shifted from Anatolia to Europe and the Balkans with the occupation of the Gallipoli peninsula in the 1350s. After the region was conquered by the Muslim Ottoman Empire, the Turkish presence grew. Some of the settlers were Yörüks, nomads who quickly became sedentary, and others were from urban classes. They settled in almost all of the towns, but the majority of them settled in the Eastern Balkans. The main areas of settlement were Ludogorie, Dobrudzha, the Thracian plain, the mountains and plains of northern Greece and Eastern Macedonia around the Vardar river.

Between the 15th and 17th centuries, large numbers of native Balkan peoples converted to Islam. Places of mass conversions were in Bosnia, Albania, North Macedonia, Kosovo, Crete, and the Rhodope Mountains. Some of the native population converted to Islam and became Turkish over time, mainly those in Anatolia.

Motives for persecution

Hall points out that atrocities were committed by all sides during the Balkan conflicts. Deliberate terror was designed to instigate population movements out of particular territories. The aim of targeting the civilian population was to carve ethnically homogeneous countries.

Great Turkish War

Further information: Siege of Buda (1686) § Massacre of Jews and Muslims

Even before the Great Turkish War (1683—1699) Austrians and Venetians supported Christian irregulars and rebellious highlanders of Herzegovina, Montenegro and Albania to raid Muslim Slavs.

The end of the Great Turkish War marked the first time the Ottoman Empire lost large areas of territory to Christians. Most of Hungary, Podolia, and the Morea was lost. The Ottomans regained the Morea quickly, and Muslims soon became part of the population or were never thoroughly displaced in the first place.

Most of the Christians who lived in the Ottoman Empire were Orthodox, so Russia was particularly interested in them. In 1711 Peter the Great invited Balkan Christians to revolt against Ottoman Muslim rule.

Hungary

After the Siege of Pécs, local Muslims were forced to convert to Catholicism between 1686 and 1713, or left the region. The city of Hatvan became a haven for Turkish merchants and became a majority Muslim settlement, but after it fell to the Hungarian troops in 1686, all Turkish settlers were forcibly expelled and their holds in the city became property of foreign mercenaries that fought in the Liberation of Buda.

Croatia

About one quarter of all people living in Slavonia in the 16th century were Muslims who mostly lived in towns, with Osijek and Požega being the largest Muslim settlements. Like other Muslims who lived in Croatia (Lika and Kordun) and Dalmatia, they were all forced to leave their homes by the end of 1699. This was the first example of the cleansing of Muslims in this region. This cleansing of Muslims "enjoyed the benediction of Catholic church". Around 130,000 Muslims from Croatia and Slavonia were driven to Ottoman Bosnia and Herzegovina. Basically, all Muslims who lived in Croatia, Slavonia and Dalmatia were either forced to exile, murdered or enslaved.

Thousands of Serb refugees crossed the Danube and populated territories of Habsburg Monarchy left by Muslims. Leopold I granted ethno-religious autonomy to them without giving any privileges to the remaining Muslim population who therefore fled to Bosnia, Herzegovina and Serbia spreading anti-Christian sentiment among other Muslims there. The relations between non-Muslim and Muslim population of Ottoman held Balkans became progressively worse.

At the beginning of the 18th century remaining Muslims of Slavonia moved to Posavina. The Ottoman authorities encouraged hopes of expelled Muslims for a quick return to their homes and settled them in the border regions. The Muslims comprised about 2/3 population of Lika. All of them, like Muslims who lived in other parts of Croatia, were forced to convert to Catholicism or to be expelled. Almost all Ottoman buildings were destroyed in Croatia, after the Ottomans left.

Northern Bosnia

In 1716, Austria occupied northern Bosnia alongside northern Serbia until 1739 when those lands were ceded back to the Ottoman Empire at the Treaty of Belgrade. During this era, the Austrian Empire outlined its position to the Bosnian Muslim population about living within its administration. Two options were offered by Charles VI such as a conversion to Christianity while retaining property and remaining on Austrian territory, or for a departure of those remaining Muslim to other lands.

Montenegro

At the beginning of the 18th century (1709 or 1711) Orthodox Serbs massacred their Muslim neighbors in Montenegro.

National movements

Serbian Revolution

Main article: First Serbian Uprising

After the Dahije, renegade janissaries who defied the Sultan and ruled the Sanjak of Smederevo in tyranny (beginning in 1801), imposing harsh taxes and forced labour, went on to execute leading Serbs throughout the sanjak in 1804, the Serbs rose up against the Dahije. The revolt, known as the First Serbian Uprising, subsequently reached national level after the quick success of the Serbs. The Porte, seeing the Serbs as a threat, ordered their disbandment. The revolutionaries took over Belgrade in 1806 where an armed uprising against a Muslim garrison, including civilians, took place. During the uprising urban centers with sizeable Muslim populations were violently targeted such as Užice and Valjevo, as the Serbian peasantry held a class hatred of the urban Muslim elite. In the end, Serbia became an autonomous country and most of the Muslims were expelled. During the revolts 15,000–20,000 Muslims fled or were expelled. In Belgrade and the rest of Serbia there remained a Muslim population of some 23,000 who were also forcibly expelled after 1862, following a massacre of Serbian civilians by Ottoman soldiers near Kalemegdan. Some Muslim families then migrated and resettled in Bosnia, where their descendants today reside in urban centres such as Šamac, Tuzla, Foča and Sarajevo.

Greek Revolution

See also: Massacre of Tripoli and Navarino massacre

In 1821, a major Greek revolt broke out in Southern Greece. Insurgents gained control of most of the countryside while the Muslims and Jews sheltered themselves in the fortified towns and castles. Each one of them was besieged and gradually through starvation or surrender most were taken over by the Greeks. In the massacres of April 1821 some 15,000 were killed. The worst massacre happened in Tripolitsa, some 8,000 Muslims and Jews died. In response, massive reprisals against Greeks in Constantinople, Smyrna, Cyprus, and elsewhere, took place; thousands were killed and the Ottoman Sultan even considered a policy of total extermination of all Greeks in the Empire. In the end an independent Greece was set up. Most of the Muslims in its area had been killed or expelled during the conflict. British historian William St Clair argues that what he calls "the genocidal process" ended when there were no more Turks to kill in what would become independent Greece.

Bulgarian uprising

Main article: April Uprising

In 1876 a Bulgarian uprising broke out in dozens of villages. The first attacks were made against the local Muslims but in a short time the Ottomans violently suppressed the uprising.

From 1876 until 1989, Muslims from Bulgaria (Turks, Tatars, Pomaks and Muslim Roma) were expelled to Turkey; such as during the Russo-Turkish War (1877–1878), Balkan Wars (1912-1913), and the 1989 expulsion of Turks from Bulgaria.

Russo-Turkish war

Bulgaria

Main article: Russo-Turkish War (1877–78)

The Bulgarian uprising eventually lead to a war between Russia and the Ottomans. Russia invaded the Ottoman Balkans through Dobrudzha and northern Bulgaria attacking the Muslim population. In this war the Ottomans were defeated, and in the process nearly half of the Muslims in Bulgaria fled to Constantinople and Anatolia. It was a cold winter and a large part of them died. Some of them returned after the war but most of these left again. The Bulgarian Muslims (part of them Turks) settled mostly around the Sea of Marmara. Some of them had been wealthy and they played an important part in the Ottoman elite in later years. Almost half of the pre-war 1,5 million Muslim population of Bulgaria was gone, an estimated 200,000 died and the rest fled.

Migration continued in the peacetime, some 350,000 Bulgarian Muslims left the country between 1880 and 1911.

Serbian–Ottoman War (1876–78)

See also: Expulsion of the Albanians 1877–1878

On the eve of the outbreak of a second round of hostilities between Serbia and the Ottoman Empire in 1877, a notable Muslim population existed in the districts of Niš, Pirot, Vranje, Leskovac, Prokuplje and Kuršumlija. The rural parts of Toplica, Kosanica, Pusta Reka and Jablanica valleys and adjoining semi-mountainous interior was inhabited by compact Muslim Albanian population while Serbs in those areas lived near the river mouths and mountain slopes and both peoples inhabited other regions of the South Morava river basin. The Muslim population of most of the area was composed out of ethnic Gheg Albanians and with Turks located in urban centres. Part of the Turks were of Albanian origin. The Muslims in the cities of Niš and Pirot were Turkish-speaking; Vranje and Leskovac were Turkish- and Albanian-speaking; Prokuplje and Kuršumlija were Albanian-speaking. There was also a minority of Circassian refugees settled by the Ottomans during the 1860s, near the then border around the environs of Niš. Estimates vary on the size of the Muslim population on the eve of the war within these areas ranging from as high as 200,000 to as low as 131,000. Estimates as to the number of the Muslim refugees that left the region for the Ottoman Empire due to the war range from 60–70,000 to as low as 30,000. The departure of the Albanian population from these regions was done in a manner that today would be characterized as ethnic cleansing.

Hostilities between Serbian and Ottoman forces broke out on 15 December 1877, after a Russian request for Serbia to enter the Russo-Turkish war. The Serbian military had two objectives: capturing Niš and breaking the Niš-Sofia Ottoman lines of communication. Serbian forces entered the wider Toplica and Morava valleys capturing urban centres such as Niš, Kuršumlija, Prokuplije, Leskovac, and Vranje and their surrounding rural and mountainous districts. In these regions, the Albanian population depending on the area they resided had fled into nearby mountains, leaving livestock, property and other belongings behind. Some Albanians returned and submitted to Serbian authorities, while others continued their flight southward toward Ottoman Kosovo. Serbian forces also encountered heavy Albanian resistance in certain areas which slowed their advance into these regions resulting in having to take villages one by one that became vacant. A small Albanian population remained the Medveđa area, where their descendants still reside today. The retreat of these refugees toward Ottoman Kosovo was halted at the Goljak Mountains when an armistice was declared. The Albanian population was resettled in Lab area and other parts of northern Kosovo alongside the new Ottoman-Serbian border. Most Albanian refugees were resettled in over 30 large rural settlements in central and southeastern Kosovo and in urban centres that increased their populations substantially. Tensions between Albanian refugees and local Kosovo Albanians arose over resources, as the Ottoman Empire found it difficult to accommodate to their needs and meager conditions. Tensions in the form of revenge attacks also arose by incoming Albanian refugees on local Kosovo Serbs that contributed to the beginnings of the ongoing Serbian-Albanian conflict in coming decades.

Bosnia

In 1875, a conflict between Muslims and Christians broke out in Bosnia. After the Ottoman Empire signed the treaty at the 1878 Berlin Congress, Bosnia was occupied by Austria-Hungary. Bosnian Muslims (Bosniaks) perceived this as a betrayal by the Ottomans and left on their own, felt that they were defending their homeland and not the wider Empire. From 9 July until 20 October 1878 or for almost three months, Bosnian Muslims resisted Austro-Hungarian forces in nearly sixty military engagements with 5,000 casualties either wounded or killed. Some Bosnian Muslims concerned about their future and well being under the new non-Muslim administration, left Bosnia for the Ottoman Empire. From 1878 until 1918, between 130,000 and 150,000 Bosnian Muslims departed Bosnia to areas under Ottoman control, some to the Balkans, others to Anatolia, the Levant and Maghreb. Today, these Bosnian populations in the Arab world have become assimilated although they have retained memories of their origins and some bear the ethnonym Bosniak (rendered in Arabic as Bushnak) as a surname.

Circassia

The Russo-Circassian War was the 101 year-long military conflict between Circassia and Russia. Circassia was de jure part of the Ottoman Empire but de facto independent. The conflict started in 1763, when the Russian Empire attempted to establish hostile forts in Circassian territory and quickly annex Circassia, followed by the Circassian refusal of the annexation; only ending 101 years later when the last resistance army of Circassia was defeated on 21 May 1864, making it exhausting and casualty heavy for the Russian Empire as well as being the single longest war Russia ever waged in history.

The end of the war saw the Circassian genocide take place in which Imperial Russia aimed to systematically destroy the Circassian people where several war crimes were committed by the Russian forces and up to 1.5 million Circassians were killed or expelled to the Middle East, especially modern-day Turkey. Russian generals such as Grigory Zass described the Circassians as "subhuman filth", and justified their killing and use in scientific experiments.

South Caucasus

The area around Kars was ceded to Russia. This resulted in a large number of Muslims leaving and settling in remaining Ottoman lands. Batum and its surrounding area was also ceded to Russia causing many local Georgian Muslims to migrate to the west. Most of them settled around the Anatolian Black Sea coast.

Balkan Wars

Main article: Balkan Wars

 

Turkish refugees running from Bulgarian hostilities, First Balkan War, 1913

In 1912 Serbia, Greece, Bulgaria and Montenegro declared war on the Ottomans. The Ottomans quickly lost territory. According to Geert-Hinrich Ahrens, "the invading armies and Christian insurgents committed a wide range of atrocities upon the Muslim population." In Kosovo and Albania most of the victims were Albanians while in other areas most of the victims were Turks and Pomaks. A large number of Pomaks in the Rhodopes were forcibly converted to Orthodoxy but later allowed to reconvert, most of them did. During this war hundreds of thousands of the Turks and Pomaks fled their villages and became refugees. The Report of the International Commission on the Balkan Wars reported that in many districts the Moslem villages were systematically burned by their Christian neighbors. In Monastir 80% of the Muslim villages were burned by the Serbian and Greek army according to a British report. While in Giannitsa the Muslim quarter was burned alongside many Muslim villages in the Salonica province by the Greek army. Massacres and rapes are also reported by the Greek and Bulgarian armies towards Turks. Arnold Toynbee gives the number of Muslim refugees who fled the region that fell under Bulgarian, Serbian and Greek control between 1912–1915 as 297,918. Justin Mccarthy gives the number of refugees during and after the Balkan Wars (1912–20) as 413,922, and further states that in the period between 1911–1926 out of the 2,315,293 Muslims that lived in the areas taken from the Ottoman Empire in Europe (excluding Albania), 812,771 ended up in Turkey (including those of the population exchange between Greece and Turkey), 632,408 died, and 870,114 remained. By 1923, only 38% of the Muslim population of 1912 still lived in the Balkans. According to Emre Erol, 410,000 Muslims were displaced to the Ottoman Empire and more than 100,000 died during their flight. Salonika (Thessaloniki) and Adrianople (Edirne) were crowded with them. By sea and land mostly they settled in Ottoman Thrace and Anatolia.

World War I and the Turkish War of Independence

Caucasus Campaign

Historian Uğur Ümit Üngör noted that during the Russian invasion of Ottoman lands, "many atrocities were carried out against the local Turks and Kurds by the Russian army and Armenian volunteers." General Liakhov gave the order to kill any Turk on sight and destroy any mosque. According to Boris Shakhovskoi the Armenian nationalists wanted to exterminate the Muslims in the occupied regions. A large part of the local Muslim Turks and Kurds fled west after the Russian invasion of 1914–1918, in Talaat Pasha's Notebook the given number is at 702,905 Turks. J. Rummel estimates that 128,000-600,000 Muslim Turks and Kurds were killed by Russian troops and Armenian irregulars; at least 128,000 of them between 1914–1915 according to Turkish statistician Ahmet Emin Yalman. After the formation of the Provisional Government in 1917, some 30,000–40,000 Muslims were killed by irregular Armenian units as retribution. Turkish-German historian Taner Akçam in book A Shameful Act writes of Vehip Pasha's detailed account of the reprisals against Muslims during the retreat of Armenian and Russian forces from Western Armenia in 1917–1918, setting the death figure at 3,000 in the Erzincan and Bayburt areas. Writing also of another eyewitness testimony claiming 3,000 dead in the Erzurum area, and 20,000 dead in Kars in the spring of 1918. Akçam also makes mention of a study of the Vilayet of Erzurum which sets the number of massacred Muslims as 25,000 in the spring of 1918, however, providing the examination of Armenian historian Vahakn Dadrian who claims from the wartime records of the Ottoman Third Army that "altogether some 5,000–5,500 victims are involved." Akçam writes of a Turkish source which describes the number of Muslim deaths during the winter and spring of 1919 in Kars as 6,500, whereas on 22 March 1920, Kâzım Karabekir put the number at 2,000 in certain villages and regions in Kars. In April 1918, 800 Muslims were massacred in the Iğdır Province—In 5 July 1920, 25,000 Muslims had been killed in Kars and Iğdır since 1918. Halil Bey in a 1919 letter to Karabekir claimed 24 villages in Iğdır had been razed.

Franco-Turkish War

Main article: Franco-Turkish War

Cilicia was occupied by the British after World War I, who were later replaced by the French. The French Armenian Legion armed returning Armenian refugees of the Armenian genocide to the region and assisting them. Eventually the Turks responded with resistance against the French occupation, battles took place in Marash, Aintab, and Urfa. Most of these cities were destroyed during the process with large civilian suffering. In Marash, 4.500 Turks died. The French left the area together with the Armenians after 1920. The retribution for the Armenian Genocide served as justification for armed Armenians.

Also during the Franco-Turkish War, the Kaç Kaç incident occurred, which refers to the escape of 40,000 Turks from the city of Adana into more mountainous regions due to the Franco-Armenian operation of July 20, 1920. During the escape, French-Armenian airplanes bombed the fleeing population and the Belemedik hospital.

Greco–Turkish War

Greek Captain Papa Grigoriou – perpetrator of Muslim massacres during the Greco-Turkish War.

 

Main articles: Greco-Turkish War (1919–22) § Greek massacres of Turks, Greco-Turkish War (1919–22) § Greek scorched-earth policy, Yalova Peninsula massacres, Menemen massacre, and Fire of Manisa

After the Greek landing and the following occupation of Western Anatolia during the Greco-Turkish War (1919–1922), the Turkish resistance activity was answered with terror against the local Muslims. Killings, rapes, and village burnings took place as the Greek Army advanced. However, as reported in a British intelligence report at the time, in general "the [Turkish] inhabitants of the occupied zone have in most cases accepted the advent of Greek rule without demur and in some cases undoubtedly prefer it to the [Turkish] Nationalist regime which seems to have been founded on terrorism". British military personnel observed that the Greek army near Uşak was warmly welcomed by the Muslim population for "being freed from the license and oppression of the [Turkish] Nationalist troops"; there were "occasional cases of misconduct" by the Greek troops against the Muslim population, and the perpetrators were prosecuted by the Greek authorities, while the "worst miscreants" were "a handful of Armenians recruited by the Greek army", who were then sent back to Constantinople.

During the Greek occupation, Greek troops and local Greeks, Armenian, and Circassian groups committed the Yalova Peninsula Massacres in early 1921 against the local Muslim population. These resulted, according to some sources, in the deaths of c. 300 of the local Muslim populace, as well c. 27 villages. Precise number of casualties is not exactly known. Statements gathered by Ottoman official, reveal a relatively low number of casualties: based on the Ottoman enquiry to which 177 survivors responded, only 35 were reported as killed, wounded or beaten or missing. This is also in accordance with Toynbee's accounts that one to two murders were enough to drive out the population. Another source estimates that barely 1.500 Muslims out of 7,000 survived in the environment of Yalova.

The Greeks advanced all the way to Central Anatolia. After the Turkish attack in 1922 the Greeks retreated and Norman M. Naimark notes that "the Greek retreat was even more devastating for the local population than the occupation". During the retreat, towns and villages were burned as part of a scorched earth policy, accompanied with massacres and rapes. During this war, a part of Western Anatolia was destroyed, large towns such as Manisa, Salihli together with many villages being burned. 3000 houses in Alaşehir. The Inter-Allied commission, consisting of British, French, American and Italian officers found that "there is a systematic plan of destruction of Turkish villages and extinction of the Muslim population." According to Marjorie Housepian, 4000 Muslims were executed in Izmir under Greek occupation.

During the war, in East Thrace (which was ceded to Greece with the Treaty of Sèvres), around 90,000 Turkish villagers fled to Bulgaria and Istanbul from the Greeks.

 

Durmuş ("Dourmouche"), a boy wounded and hand cut off during the Yalova peninsula massacres.

After the war, peace talks between Greece and Turkey started with the Lausanne Conference of 1922–1923. At the Conference, the chief negotiator of the Turkish delegation, Ismet Pasha, gave an estimate of 1.5 million Anatolian Turks that had been exiled or died in the area of Greek occupation. Of these, McCarthy estimates that 860,000 fled and 640,000 died; with many, if not most of those who died, being refugees as well. The comparison of census figures shows that 1,246,068 Anatolian Muslims had become refugees or had died. Furthermore, Ismet Pasha shared statistics showing the destruction of 141,874 buildings, and the slaughter or theft of 3,291,335 farm animals in the area of Greek occupation. The peace that followed the Greco–Turkish War resulted in a population exchange between Greece and Turkey. As a result, the Muslim population of Greece, with the exception of Western Thrace, and partially, the Muslim Cham Albanians, was relocated to Turkey.

Total casualties

The forced mass displacement of Muslims out of the Balkans during the era of territorial contraction of the Ottoman Empire has only become a topic of recent scholarly interest in the 21st century.

Death toll

According to historian Justin McCarthy, between the years 1821–1922, from the beginning of the Greek War of Independence to the end of the Ottoman Empire, five million Muslims were driven from their lands and another five and a half million died, some of them killed in wars, others perishing as refugees from starvation or disease. However, McCarthy's work has faced harsh criticism by many scholars who have characterized his views as indefensibly biased towards Turkey and defending Turkish atrocities against Armenians, as well as engaging in genocide denial.

According to Matthew Gibney, the total Muslim refugees during these centuries are estimated to be several millions. Roger Owen estimates that during the last decade of the Ottoman Empire (1912–1922) when the Balkan wars, World War I and war of Independence took place, close to 2 million Muslims, civilian and military, died in the area of modern Turkey.

Settlement of refugees

The Ottoman authorities and charities provided some help to the immigrants and sometimes settled them in certain locations. In Turkey most of the Balkan refugees settled in Western Turkey and Thrace. The Caucasians, in addition to these areas also settled in Central Anatolia and around the Black Sea coast. Eastern Anatolia was not largely settled with the exception of some Circassian and Karapapak villages. There were also completely new villages founded by refugees, for example in uninhabited forested areas. Many people of the 1924 exchange were settled in former Greek villages along the Aegean coast. Outside of Turkey, Circassians were settled along the Hedjaz Railway and some Cretan Muslims at Syria's coast.

Academic debate

According to Michael Mann McCarthy is often viewed as a scholar on the Turkish side of the debate over Balkan Muslim death figures. Mann however states that even if those figures were reduced "by as much as 50 percent, they still would horrify". In the discussion about the Armenian Genocide, McCarthy denies the genocide and is considered as the leading pro-Turkish scholar. Scholarly critics of McCarthy acknowledge that his research on Muslim civilian casualties and refugee numbers (19th and early 20th centuries) has brought forth a valuable perspective, previously neglected in the Christian West: that millions of Muslims and Jews also suffered and died during these years. Donald W. Bleacher, though acknowledging that McCarthy is pro-Turkish nonetheless has called his scholarly study Death and Exile on Muslim civilian casualties and refugee numbers "a necessary corrective" challenging the West's model of all victims being Christians and all perpetrators as being Muslims.

Historian Mark Biondich estimates that from 1878–1912 up to two million Muslims left the Balkans either voluntarily or involuntarily while Muslims casualties in the Balkans during 1912–1923 within the context of those killed and expelled exceeded some three million.

Destruction of Muslim heritage

Muslim heritage was extensively targeted during the persecutions. During their long rule the Ottomans had built numerous mosques, madrasas, caravanserais, bath-houses and other types of building. According to current research, around 20,000 buildings of all sizes have been documented in official Ottoman registers. However very little survives of this Ottoman heritage in most Balkan countries. Most of the Ottoman era mosques of the Balkans have been destroyed; the ones still standing often had their minarets destroyed. Before the Habsburg conquest, Osijek had 8–10 mosques, none of which remain today. During the Balkan wars there were cases of desecration, destruction of mosques and Muslim cemeteries. Of the 166 madrasas in the Ottoman Balkans in the 17th century, only eight remain and five of them are near Edirne. It is estimated that 95–98% were destroyed. The same is also valid for other types of buildings, such as markethalls, caravanserais and baths. From a chain of caravanserais across the Balkans only one is preserved while there are vague ruins of four others. There were in the area of Negroponte in 1521: 34 large and small mosques, six hamams, ten schools, and 6 dervish convents. Today only the ruin of one hamam remains.

Destruction of Ottoman mosques.

Town	During Ottoman rule	Still standing
Shumen	40	3
Serres	60	3
Belgrade	>100	1
Sofia	>100	1
Ruse	36	1
Sremska Mitrovica	17	0
Osijek	7	0
Požega	14—15	0

Commemoration

There exists literature in Turkey dealing with these events, but outside of Turkey, the events are largely unknown to the world public.

Impact on Europe

According to Mark Levene, the Victorian public in the 1870s paid much more attention to the massacres and expulsions of Christians than to massacres and expulsions of Muslims, even if on a greater scale. He further suggests that such massacres were even favored by some circles. Mark Levene also argues that the dominant powers, by supporting "nation-statism" at the Congress of Berlin, legitimized "the primary instrument of Balkan nation-building": ethnic cleansing.

Memorials

Iğdır Genocide Memorial and Museum

There is a monument in Iğdır, Turkey, called Iğdır Genocide Memorial and Museum, remembering the Muslim victims of World War I.

A monument was erected in Anaklia, Georgia on 21 May 2012, to commemorate the expulsion of the Circassians.