Factorization

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Factorization

The polynomial x² + cx + d, where a + b = c and ab = d, can be factorized into (x + a)(x + b).

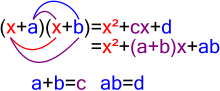
In mathematics, factorization (or factorisation, see English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller or simpler objects of the same kind. For example, 3 × 5 is an integer factorization of 15, and (x – 2)(x + 2) is a polynomial factorization of x² – 4.

Factorization is not usually considered meaningful within number systems possessing division, such as the real or complex numbers, since any ${\displaystyle x}$ can be trivially written as ${\displaystyle (xy)\times (1/y)}$ whenever ${\displaystyle y}$ is not zero. However, a meaningful factorization for a rational number or a rational function can be obtained by writing it in lowest terms and separately factoring its numerator and denominator.

Factorization was first considered by ancient Greek mathematicians in the case of integers. They proved the fundamental theorem of arithmetic, which asserts that every positive integer may be factored into a product of prime numbers, which cannot be further factored into integers greater than 1. Moreover, this factorization is unique up to the order of the factors. Although integer factorization is a sort of inverse to multiplication, it is much more difficult algorithmically, a fact which is exploited in the RSA cryptosystem to implement public-key cryptography.

Polynomial factorization has also been studied for centuries. In elementary algebra, factoring a polynomial reduces the problem of finding its roots to finding the roots of the factors. Polynomials with coefficients in the integers or in a field possess the unique factorization property, a version of the fundamental theorem of arithmetic with prime numbers replaced by irreducible polynomials. In particular, a univariate polynomial with complex coefficients admits a unique (up to ordering) factorization into linear polynomials: this is a version of the fundamental theorem of algebra. In this case, the factorization can be done with root-finding algorithms. The case of polynomials with integer coefficients is fundamental for computer algebra. There are efficient computer algorithms for computing (complete) factorizations within the ring of polynomials with rational number coefficients (see factorization of polynomials).

A commutative ring possessing the unique factorization property is called a unique factorization domain. There are number systems, such as certain rings of algebraic integers, which are not unique factorization domains. However, rings of algebraic integers satisfy the weaker property of Dedekind domains: ideals factor uniquely into prime ideals.

Factorization may also refer to more general decompositions of a mathematical object into the product of smaller or simpler objects. For example, every function may be factored into the composition of a surjective function with an injective function. Matrices possess many kinds of matrix factorizations. For example, every matrix has a unique LUP factorization as a product of a lower triangular matrix L with all diagonal entries equal to one, an upper triangular matrix U, and a permutation matrix P; this is a matrix formulation of Gaussian elimination.

Integers

Main article: Integer factorization

By the fundamental theorem of arithmetic, every integer greater than 1 has a unique (up to the order of the factors) factorization into prime numbers, which are those integers which cannot be further factorized into the product of integers greater than one.

For computing the factorization of an integer n, one needs an algorithm for finding a divisor q of n or deciding that n is prime. When such a divisor is found, the repeated application of this algorithm to the factors q and n / q gives eventually the complete factorization of n.

For finding a divisor q of n, if any, it suffices to test all values of q such that 1 < q and q² ≤ n. In fact, if r is a divisor of n such that r² > n, then q = n / r is a divisor of n such that q² ≤ n.

If one tests the values of q in increasing order, the first divisor that is found is necessarily a prime number, and the cofactor r = n / q cannot have any divisor smaller than q. For getting the complete factorization, it suffices thus to continue the algorithm by searching a divisor of r that is not smaller than q and not greater than √r.

There is no need to test all values of q for applying the method. In principle, it suffices to test only prime divisors. This needs to have a table of prime numbers that may be generated for example with the sieve of Eratosthenes. As the method of factorization does essentially the same work as the sieve of Eratosthenes, it is generally more efficient to test for a divisor only those numbers for which it is not immediately clear whether they are prime or not. Typically, one may proceed by testing 2, 3, 5, and the numbers > 5, whose last digit is 1, 3, 7, 9 and the sum of digits is not a multiple of 3.

This method works well for factoring small integers, but is inefficient for larger integers. For example, Pierre de Fermat was unable to discover that the 6th Fermat number

${\displaystyle 1+2^{2^5}=1+2^{32}=4294967297}$

is not a prime number. In fact, applying the above method would require more than 10000 divisions, for a number that has 10 decimal digits.

There are more efficient factoring algorithms. However they remain relatively inefficient, as, with the present state of the art, one cannot factorize, even with the more powerful computers, a number of 500 decimal digits that is the product of two randomly chosen prime numbers. This ensures the security of the RSA cryptosystem, which is widely used for secure internet communication.

Example

For factoring n = 1386 into primes:

• Start with division by 2: the number is even, and n = 2 · 693. Continue with 693, and 2 as a first divisor candidate.
• 693 is odd (2 is not a divisor), but is a multiple of 3: one has 693 = 3 · 231 and n = 2 · 3 · 231. Continue with 231, and 3 as a first divisor candidate.
• 231 is also a multiple of 3: one has 231 = 3 · 77, and thus n = 2 · 3² · 77. Continue with 77, and 3 as a first divisor candidate.
• 77 is not a multiple of 3, since the sum of its digits is 14, not a multiple of 3. It is also not a multiple of 5 because its last digit is 7. The next odd divisor to be tested is 7. One has 77 = 7 · 11, and thus n = 2 · 3² · 7 · 11. This shows that 7 is prime (easy to test directly). Continue with 11, and 7 as a first divisor candidate.
• As 7² > 11, one has finished. Thus 11 is prime, and the prime factorization is

1386 = 2 · 3² · 7 · 11.

Expressions

Manipulating expressions is the basis of algebra. Factorization is one of the most important methods for expression manipulation for several reasons. If one can put an equation in a factored form E⋅F = 0, then the problem of solving the equation splits into two independent (and generally easier) problems E = 0 and F = 0. When an expression can be factored, the factors are often much simpler, and may thus offer some insight on the problem. For example,

${\displaystyle x^3-a{x}^2-b{x}^2-c{x}^2+abx+acx+bcx-abc}$

having 16 multiplications, 4 subtractions and 3 additions, may be factored into the much simpler expression

${\displaystyle (x-a)(x-b)(x-c),}$

with only two multiplications and three subtractions. Moreover, the factored form immediately gives roots x = a,b,c as the roots of the polynomial.

On the other hand, factorization is not always possible, and when it is possible, the factors are not always simpler. For example, ${\displaystyle x^{10}-1}$ can be factored into two irreducible factors ${\displaystyle x-1}$ and ${\displaystyle x^9+x^8+\cdots +x^2+x+1}$.

Various methods have been developed for finding factorizations; some are described below.

Solving algebraic equations may be viewed as a problem of polynomial factorization. In fact, the fundamental theorem of algebra can be stated as follows: every polynomial in x of degree n with complex coefficients may be factorized into n linear factors ${\displaystyle x-a_i,}$ for i = 1, ..., n, where the a_is are the roots of the polynomial. Even though the structure of the factorization is known in these cases, the a_is generally cannot be computed in terms of radicals (n^th roots), by the Abel–Ruffini theorem. In most cases, the best that can be done is computing approximate values of the roots with a root-finding algorithm.

History of factorization of expressions

The systematic use of algebraic manipulations for simplifying expressions (more specifically equations)) may be dated to 9th century, with al-Khwarizmi's book The Compendious Book on Calculation by Completion and Balancing, which is titled with two such types of manipulation.

However, even for solving quadratic equations, the factoring method was not used before Harriot's work published in 1631, ten years after his death. In his book Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas, Harriot drew tables for addition, subtraction, multiplication and division of monomials, binomials, and trinomials. Then, in a second section, he set up the equation aa − ba + ca = + bc, and showed that this matches the form of multiplication he had previously provided, giving the factorization (a − b)(a + c).

General methods

The following methods apply to any expression that is a sum, or that may be transformed into a sum. Therefore, they are most often applied to polynomials, though they also may be applied when the terms of the sum are not monomials, that is, the terms of the sum are a product of variables and constants.

Common factor

It may occur that all terms of a sum are products and that some factors are common to all terms. In this case, the distributive law allows factoring out this common factor. If there are several such common factors, it is preferable to divide out the greatest such common factor. Also, if there are integer coefficients, one may factor out the greatest common divisor of these coefficients.

For example,

${\displaystyle 6x^3{y}^2+8x^4{y}^3-10x^5{y}^3=2x^3{y}^2(3+4xy-5x^{2}y),}$

since 2 is the greatest common divisor of 6, 8, and 10, and ${\displaystyle x^3{y}^2}$ divides all terms.

Grouping

Grouping terms may allow using other methods for getting a factorization.

For example, to factor

${\displaystyle 4x^2+20x+3xy+15y,}$

one may remark that the first two terms have a common factor x, and the last two terms have the common factor y. Thus

${\displaystyle 4x^2+20x+3xy+15y=(4x^2+20x)+(3xy+15y)=4x(x+5)+3y(x+5).}$

Then a simple inspection shows the common factor x + 5, leading to the factorization

${\displaystyle 4x^2+20x+3xy+15y=(4x+3y)(x+5).}$

In general, this works for sums of 4 terms that have been obtained as the product of two binomials. Although not frequently, this may work also for more complicated examples.

Adding and subtracting terms

Sometimes, some term grouping reveals part of a recognizable pattern. It is then useful to add and subtract terms to complete the pattern.

A typical use of this is the completing the square method for getting the quadratic formula.

Another example is the factorization of ${\displaystyle x^4+1.}$ If one introduces the non-real square root of –1, commonly denoted i, then one has a difference of squares

${\displaystyle x^4+1=(x^2+i)(x^2-i).}$

However, one may also want a factorization with real number coefficients. By adding and subtracting ${\displaystyle 2x^2,}$ and grouping three terms together, one may recognize the square of a binomial:

${\displaystyle x^4+1=(x^4+2x^2+1)-2x^2=(x^2+1{)}^2-{\left(x\sqrt{2}\right)}^2=\left(x^2+x\sqrt{2}+1\right)\left(x^2-x\sqrt{2}+1\right).}$

Subtracting and adding ${\displaystyle 2x^2}$ also yields the factorization:

${\displaystyle x^4+1=(x^4-2x^2+1)+2x^2=(x^2-1{)}^2+{\left(x\sqrt{2}\right)}^2=\left(x^2+x\sqrt{-2}-1\right)\left(x^2-x\sqrt{-2}-1\right).}$

These factorizations work not only over the complex numbers, but also over any field, where either –1, 2 or –2 is a square. In a finite field, the product of two non-squares is a square; this implies that the polynomial ${\displaystyle x^4+1,}$ which is irreducible over the integers, is reducible modulo every prime number. For example,

${\displaystyle x^4+1\equiv (x+1{)}^4(\mathrm{mod}2);}$

${\displaystyle x^4+1\equiv (x^2+x-1)(x^2-x-1)(\mathrm{mod}3),}$since ${\displaystyle 1^2\equiv -2(\mathrm{mod}3);}$

${\displaystyle x^4+1\equiv (x^2+2)(x^2-2)(\mathrm{mod}5),}$since ${\displaystyle 2^2\equiv -1(\mathrm{mod}5);}$

${\displaystyle x^4+1\equiv (x^2+3x+1)(x^2-3x+1)(\mathrm{mod}7),}$since ${\displaystyle 3^2\equiv 2(\mathrm{mod}7).}$

Recognizable patterns

Many identities provide an equality between a sum and a product. The above methods may be used for letting the sum side of some identity appear in an expression, which may therefore be replaced by a product.

Below are identities whose left-hand sides are commonly used as patterns (this means that the variables E and F that appear in these identities may represent any subexpression of the expression that has to be factorized).

Visual proof of the differences between two squares and two cubes

• Difference of two squares

${\displaystyle E^2-F^2=(E+F)(E-F)}$

For example,

${\displaystyle \begin{array}{rl}{a}^2+& 2ab+b^2-x^2+2xy-y^2\\ & =(a^2+2ab+b^2)-(x^2-2xy+y^2)\\ & =(a+b{)}^2-(x-y{)}^2\\ & =(a+b+x-y)(a+b-x+y).\end{array}}$

• Sum/difference of two cubes

${\displaystyle E^3+F^3=(E+F)(E^2-EF+F^2)}$

${\displaystyle E^3-F^3=(E-F)(E^2+EF+F^2)}$

• Difference of two fourth powers

${\displaystyle \begin{array}{rl}{E}^4-F^4& =(E^2+F^2)(E^2-F^2)\\ & =(E^2+F^2)(E+F)(E-F)\end{array}}$

• Sum/difference of two nth powers

In the following identities, the factors may often be further factorized:

• Difference, even exponent

${\displaystyle E^{2n}-F^{2n}=(E^n+F^n)(E^n-F^n)}$

• Difference, even or odd exponent

${\displaystyle E^n-F^n=(E-F)(E^{n-1}+E^{n-2}F+E^{n-3}{F}^2+\cdots +E{F}^{n-2}+F^{n-1})}$

This is an example showing that the factors may be much larger than the sum that is factorized.

• Sum, odd exponent

${\displaystyle E^n+F^n=(E+F)(E^{n-1}-E^{n-2}F+E^{n-3}{F}^2-\cdots -E{F}^{n-2}+F^{n-1})}$

(obtained by changing F by –F in the preceding formula)

• Sum, even exponent

If the exponent is a power of two then the expression cannot, in general, be factorized without introducing complex numbers (if E and F contain complex numbers, this may be not the case). If n has an odd divisor, that is if n = pq with p odd, one may use the preceding formula (in "Sum, odd exponent") applied to ${\displaystyle (E^q{)}^p+(F^q{)}^p.}$

• Trinomials and cubic formulas

${\displaystyle \begin{array}{rl}& x^2+y^2+z^2+2(xy+yz+xz)=(x+y+z{)}^2\\ & x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-xy-xz-yz)\\ & x^3+y^3+z^3+3x^2(y+z)+3y^2(x+z)+3z^2(x+y)+6xyz=(x+y+z{)}^3\\ & x^4+x^2{y}^2+y^4=(x^2+xy+y^2)(x^2-xy+y^2).\end{array}}$

• Binomial expansions

Visualisation of binomial expansion up to the 4th power

The binomial theorem supplies patterns that can easily be recognized from the integers that appear in them

In low degree:

${\displaystyle a^2+2ab+b^2=(a+b{)}^2}$

${\displaystyle a^2-2ab+b^2=(a-b{)}^2}$

${\displaystyle a^3+3a^{2}b+3a{b}^2+b^3=(a+b{)}^3}$

${\displaystyle a^3-3a^{2}b+3a{b}^2-b^3=(a-b{)}^3}$

More generally, the coefficients of the expanded forms of ${\displaystyle (a+b{)}^n}$ and ${\displaystyle (a-b{)}^n}$ are the binomial coefficients, that appear in the nth row of Pascal's triangle.

Roots of unity

The nth roots of unity are the complex numbers each of which is a root of the polynomial ${\displaystyle x^n-1.}$ They are thus the numbers

${\displaystyle e^{2ik\pi /n}=\cos \frac{2\pi k}{n}+i\sin \frac{2\pi k}{n}}$

for ${\displaystyle k=0,\dots ,n-1.}$

It follows that for any two expressions E and F, one has:

${\displaystyle E^n-F^n=(E-F)\prod _{k=1}^{n-1}\left(E-F{e}^{2ik\pi /n}\right)}$

${\displaystyle E^n+F^n=\prod _{k=0}^{n-1}\left(E-F{e}^{(2k+1)i\pi /n}\right)\text{if }n\text{ is even}}$

${\displaystyle E^n+F^n=(E+F)\prod _{k=1}^{n-1}\left(E+F{e}^{2ik\pi /n}\right)\text{if }n\text{ is odd}}$

If E and F are real expressions, and one wants real factors, one has to replace every pair of complex conjugate factors by its product. As the complex conjugate of ${\displaystyle e^{i\alpha }}$ is ${\displaystyle e^{-i\alpha },}$ and

${\displaystyle \left(a-b{e}^{i\alpha }\right)\left(a-b{e}^{-i\alpha }\right)=a^2-ab\left(e^{i\alpha }+e^{-i\alpha }\right)+b^2{e}^{i\alpha }{e}^{-i\alpha }=a^2-2ab\cos \alpha +b^2,}$

one has the following real factorizations (one passes from one to the other by changing k into n – k or n + 1 – k, and applying the usual trigonometric formulas:

${\displaystyle \begin{array}{rl}{E}^{2n}-F^{2n}& =(E-F)(E+F)\prod _{k=1}^{n-1}\left(E^2-2EF\cos \frac{k\pi }{n}+F^2\right)\\ & =(E-F)(E+F)\prod _{k=1}^{n-1}\left(E^2+2EF\cos \frac{k\pi }{n}+F^2\right)\end{array}}$

${\displaystyle \begin{array}{rl}{E}^{2n}+F^{2n}& =\prod _{k=1}^n\left(E^2+2EF\cos \frac{(2k-1)\pi }{2n}+F^2\right)\\ & =\prod _{k=1}^n\left(E^2-2EF\cos \frac{(2k-1)\pi }{2n}+F^2\right)\end{array}}$

The cosines that appear in these factorizations are algebraic numbers, and may be expressed in terms of radicals (this is possible because their Galois group is cyclic); however, these radical expressions are too complicated to be used, except for low values of n. For example,

${\displaystyle a^4+b^4=(a^2-\sqrt{2}ab+b^2)(a^2+\sqrt{2}ab+b^2).}$

${\displaystyle a^5-b^5=(a-b)\left(a^2+\frac{1-\sqrt{5}}{2}ab+b^2\right)\left(a^2+\frac{1+\sqrt{5}}{2}ab+b^2\right),}$

${\displaystyle a^5+b^5=(a+b)\left(a^2-\frac{1-\sqrt{5}}{2}ab+b^2\right)\left(a^2-\frac{1+\sqrt{5}}{2}ab+b^2\right),}$

Often one wants a factorization with rational coefficients. Such a factorization involves cyclotomic polynomials. To express rational factorizations of sums and differences or powers, we need a notation for the homogenization of a polynomial: if ${\displaystyle P(x)=a_0{x}^n+a_i{x}^{n-1}+\cdots +a_n,}$ its homogenization is the bivariate polynomial ${\displaystyle \overline{P}(x,y)=a_0{x}^n+a_i{x}^{n-1}y+\cdots +a_n{y}^n.}$ Then, one has

${\displaystyle E^n-F^n=\prod _{k\mid n}{\overline{Q}}_n(E,F),}$

${\displaystyle E^n+F^n=\prod _{k\mid 2n,k\nmid n}{\overline{Q}}_n(E,F),}$

where the products are taken over all divisors of n, or all divisors of 2n that do not divide n, and ${\displaystyle Q_n(x)}$ is the nth cyclotomic polynomial.

For example,

${\displaystyle a^6-b^6={\overline{Q}}_1(a,b){\overline{Q}}_2(a,b){\overline{Q}}_3(a,b){\overline{Q}}_6(a,b)=(a-b)(a+b)(a^2-ab+b^2)(a^2+ab+b^2),}$

${\displaystyle a^6+b^6={\overline{Q}}_4(a,b){\overline{Q}}_{12}(a,b)=(a^2+b^2)(a^4-a^2{b}^2+b^4),}$

since the divisors of 6 are 1, 2, 3, 6, and the divisors of 12 that do not divide 6 are 4 and 12.

Polynomials

Main article: Factorization of polynomials

For polynomials, factorization is strongly related with the problem of solving algebraic equations. An algebraic equation has the form

${\displaystyle P(x)\stackrel{\text{def}}{=}{a}_0{x}^n+a_1{x}^{n-1}+\cdots +a_n=0,}$

where P(x) is a polynomial in x with ${\displaystyle a_0\ne 0.}$ A solution of this equation (also called a root of the polynomial) is a value r of x such that

${\displaystyle P(r)=0.}$

If ${\displaystyle P(x)=Q(x)R(x)}$ is a factorization of P(x) = 0 as a product of two polynomials, then the roots of P(x) are the union of the roots of Q(x) and the roots of R(x). Thus solving P(x) = 0 is reduced to the simpler problems of solving Q(x) = 0 and R(x) = 0.

Conversely, the factor theorem asserts that, if r is a root of P(x) = 0, then P(x) may be factored as

${\displaystyle P(x)=(x-r)Q(x),}$

where Q(x) is the quotient of Euclidean division of P(x) = 0 by the linear (degree one) factor x – r.

If the coefficients of P(x) are real or complex numbers, the fundamental theorem of algebra asserts that P(x) has a real or complex root. Using the factor theorem recursively, it results that

${\displaystyle P(x)=a_0(x-r_1)\cdots (x-r_n),}$

where ${\displaystyle r_1,\dots ,r_n}$ are the real or complex roots of P, with some of them possibly repeated. This complete factorization is unique up to the order of the factors.

If the coefficients of P(x) are real, one generally wants a factorization where factors have real coefficients. In this case, the complete factorization may have some quadratic (degree two) factors. This factorization may easily be deduced from the above complete factorization. In fact, if r = a + ib is a non-real root of P(x), then its complex conjugate s = a - ib is also a root of P(x). So, the product

${\displaystyle (x-r)(x-s)=x^2-(r+s)x+rs=x^2-2ax+a^2+b^2}$

is a factor of P(x) with real coefficients. Repeating this for all non-real factors gives a factorization with linear or quadratic real factors.

For computing these real or complex factorizations, one needs the roots of the polynomial, which may not be computed exactly, and only approximated using root-finding algorithms.

In practice, most algebraic equations of interest have integer or rational coefficients, and one may want a factorization with factors of the same kind. The fundamental theorem of arithmetic may be generalized to this case, stating that polynomials with integer or rational coefficients have the unique factorization property. More precisely, every polynomial with rational coefficients may be factorized in a product

${\displaystyle P(x)=q{P}_1(x)\cdots P_k(x),}$

where q is a rational number and ${\displaystyle P_1(x),\dots ,P_k(x)}$ are non-constant polynomials with integer coefficients that are irreducible and primitive; this means that none of the ${\displaystyle P_i(x)}$ may be written as the product two polynomials (with integer coefficients) that are neither 1 nor –1 (integers are considered as polynomials of degree zero). Moreover, this factorization is unique up to the order of the factors and the signs of the factors.

There are efficient algorithms for computing this factorization, which are implemented in most computer algebra systems. See Factorization of polynomials. Unfortunately, these algorithms are too complicated to use for paper-and-pencil computations. Besides the heuristics above, only a few methods are suitable for hand computations, which generally work only for polynomials of low degree, with few nonzero coefficients. The main such methods are described in next subsections.

Primitive-part & content factorization

Main article: Polynomial factorization § Primitive part–content factorization

Every polynomial with rational coefficients, may be factorized, in a unique way, as the product of a rational number and a polynomial with integer coefficients, which is primitive (that is, the greatest common divisor of the coefficients is 1), and has a positive leading coefficient (coefficient of the term of the highest degree). For example:

${\displaystyle -10x^2+5x+5=(-5)\cdot (2x^2-x-1)}$

${\displaystyle \frac{1}{3}{x}^5+\frac{7}{2}{x}^2+2x+1=\frac{1}{6}(2x^5+21x^2+12x+6)}$

In this factorization, the rational number is called the content, and the primitive polynomial is the primitive part. The computation of this factorization may be done as follows: firstly, reduce all coefficients to a common denominator, for getting the quotient by an integer q of a polynomial with integer coefficients. Then one divides out the greater common divisor p of the coefficients of this polynomial for getting the primitive part, the content being ${\displaystyle p/q.}$ Finally, if needed, one changes the signs of p and all coefficients of the primitive part.

This factorization may produce a result that is larger than the original polynomial (typically when there are many coprime denominators), but, even when this is the case, the primitive part is generally easier to manipulate for further factorization.

Using the factor theorem

Main article: Factor theorem

The factor theorem states that, if r is a root of a polynomial

${\displaystyle P(x)=a_0{x}^n+a_1{x}^{n-1}+\cdots +a_{n-1}x+a_n,}$

meaning P(r) = 0, then there is a factorization

${\displaystyle P(x)=(x-r)Q(x),}$

where

${\displaystyle Q(x)=b_0{x}^{n-1}+\cdots +b_{n-2}x+b_{n-1},}$

with ${\displaystyle a_0=b_0}$. Then polynomial long division or synthetic division give:

${\displaystyle b_i=a_0{r}^i+\cdots +a_{i-1}r+a_i\text{ for }i=1,\dots ,n-1.}$

This may be useful when one knows or can guess a root of the polynomial.

For example, for ${\displaystyle P(x)=x^3-3x+2,}$ one may easily see that the sum of its coefficients is 0, so r = 1 is a root. As r + 0 = 1, and ${\displaystyle r^2+0r-3=-2,}$ one has

${\displaystyle x^3-3x+2=(x-1)(x^2+x-2).}$

Rational roots

For polynomials with rational number coefficients, one may search for roots which are rational numbers. Primitive part-content factorization (see above) reduces the problem of searching for rational roots to the case of polynomials with integer coefficients having no non-trivial common divisor.

If ${\displaystyle x=\frac{p}{q}}$ is a rational root of such a polynomial

${\displaystyle P(x)=a_0{x}^n+a_1{x}^{n-1}+\cdots +a_{n-1}x+a_n,}$

the factor theorem shows that one has a factorization

${\displaystyle P(x)=(qx-p)Q(x),}$

where both factors have integer coefficients (the fact that Q has integer coefficients results from the above formula for the quotient of P(x) by ${\displaystyle x-p/q}$).

Comparing the coefficients of degree n and the constant coefficients in the above equality shows that, if ${\displaystyle \frac{p}{q}}$ is a rational root in reduced form, then q is a divisor of ${\displaystyle a_0,}$ and p is a divisor of ${\displaystyle a_n.}$ Therefore, there is a finite number of possibilities for p and q, which can be systematically examined.

For example, if the polynomial

${\displaystyle P(x)=2x^3-7x^2+10x-6}$

has a rational root ${\displaystyle \frac{p}{q}}$ with q > 0, then p must divide 6; that is ${\displaystyle p\in \{\pm 1,\pm 2,\pm 3,\pm 6\},}$ and q must divide 2, that is ${\displaystyle q\in \{1,2\}.}$ Moreover, if x < 0, all terms of the polynomial are negative, and, therefore, a root cannot be negative. That is, one must have

${\displaystyle \frac{p}{q}\in \{1,2,3,6,\frac{1}{2},\frac{3}{2}\}.}$

A direct computation shows that only ${\displaystyle \frac{3}{2}}$ is a root, so there can be no other rational root. Applying the factor theorem leads finally to the factorization ${\displaystyle 2x^3-7x^2+10x-6=(2x-3)(x^2-2x+2).}$

Quadratic ac method

The above method may be adapted for quadratic polynomials, leading to the ac method of factorization.

Consider the quadratic polynomial

${\displaystyle P(x)=a{x}^2+bx+c}$

with integer coefficients. If it has a rational root, its denominator must divide a evenly and it may be written as a possibly reducible fraction ${\displaystyle r_1=\frac{r}{a}.}$ By Vieta's formulas, the other root ${\displaystyle r_2}$ is

${\displaystyle r_2=-\frac{b}{a}-r_1=-\frac{b}{a}-\frac{r}{a}=-\frac{b+r}{a}=\frac{s}{a},}$

with ${\displaystyle s=-(b+r).}$ Thus the second root is also rational, and Vieta's second formula ${\displaystyle r_1{r}_2=\frac{c}{a}}$ gives

${\displaystyle \frac{s}{a}\frac{r}{a}=\frac{c}{a},}$

that is

${\displaystyle rs=ac\text{and}r+s=-b.}$

Checking all pairs of integers whose product is ac gives the rational roots, if any.

In summary, if ${\displaystyle a{x}^2+bx+c}$ has rational roots there are integers r and s such ${\displaystyle rs=ac}$ and ${\displaystyle r+s=-b}$ (a finite number of cases to test), and the roots are ${\displaystyle \frac{r}{a}}$ and ${\displaystyle \frac{s}{a}.}$ In other words, one has the factorization

${\displaystyle a(a{x}^2+bx+c)=(ax-r)(ax-s).}$

For example, let consider the quadratic polynomial

${\displaystyle 6x^2+13x+6.}$

Inspection of the factors of ac = 36 leads to 4 + 9 = 13 = b, giving the two roots

${\displaystyle r_1=-\frac{4}{6}=-\frac{2}{3}\text{and}{r}_2=-\frac{9}{6}=-\frac{3}{2},}$

and the factorization

${\displaystyle 6x^2+13x+6=6(x+\frac{2}{3})(x+\frac{3}{2})=(3x+2)(2x+3).}$

Using formulas for polynomial roots

Any univariate quadratic polynomial ${\displaystyle a{x}^2+bx+c}$ can be factored using the quadratic formula:

${\displaystyle a{x}^2+bx+c=a(x-\alpha )(x-\beta )=a\left(x-\frac{-b+\sqrt{b^2-4ac}}{2a}\right)\left(x-\frac{-b-\sqrt{b^2-4ac}}{2a}\right),}$

where ${\displaystyle \alpha }$ and ${\displaystyle \beta }$ are the two roots of the polynomial.

If a, b, c are all real, the factors are real if and only if the discriminant ${\displaystyle b^2-4ac}$ is non-negative. Otherwise, the quadratic polynomial cannot be factorized into non-constant real factors.

The quadratic formula is valid when the coefficients belong to any field of characteristic different from two, and, in particular, for coefficients in a finite field with an odd number of elements.

There are also formulas for roots of cubic and quartic polynomials, which are, in general, too complicated for practical use. The Abel–Ruffini theorem shows that there are no general root formulas in terms of radicals for polynomials of degree five or higher.

Using relations between roots

It may occur that one knows some relationship between the roots of a polynomial and its coefficients. Using this knowledge may help factoring the polynomial and finding its roots. Galois theory is based on a systematic study of the relations between roots and coefficients, that include Vieta's formulas.

Here, we consider the simpler case where two roots ${\displaystyle x_1}$ and ${\displaystyle x_2}$ of a polynomial ${\displaystyle P(x)}$ satisfy the relation

${\displaystyle x_2=Q(x_1),}$

where Q is a polynomial.

This implies that ${\displaystyle x_1}$ is a common root of ${\displaystyle P(Q(x))}$ and ${\displaystyle P(x).}$ It is therefore a root of the greatest common divisor of these two polynomials. It follows that this greatest common divisor is a non constant factor of ${\displaystyle P(x).}$ Euclidean algorithm for polynomials allows computing this greatest common factor.

For example, if one know or guess that: ${\displaystyle P(x)=x^3-5x^2-16x+80}$ has two roots that sum to zero, one may apply Euclidean algorithm to ${\displaystyle P(x)}$ and ${\displaystyle P(-x).}$ The first division step consists in adding ${\displaystyle P(x)}$ to ${\displaystyle P(-x),}$ giving the remainder of

${\displaystyle -10(x^2-16).}$

Then, dividing ${\displaystyle P(x)}$ by ${\displaystyle x^2-16}$ gives zero as a new remainder, and x – 5 as a quotient, leading to the complete factorization

${\displaystyle x^3-5x^2-16x+80=(x-5)(x-4)(x+4).}$

Unique factorization domains

The integers and the polynomials over a field share the property of unique factorization, that is, every nonzero element may be factored into a product of an invertible element (a unit, ±1 in the case of integers) and a product of irreducible elements (prime numbers, in the case of integers), and this factorization is unique up to rearranging the factors and shifting units among the factors. Integral domains which share this property are called unique factorization domains (UFD).

Greatest common divisors exist in UFDs, and conversely, every integral domain in which greatest common divisors exist is an UFD. Every principal ideal domain is an UFD.

A Euclidean domain is an integral domain on which is defined a Euclidean division similar to that of integers. Every Euclidean domain is a principal ideal domain, and thus a UFD.

In a Euclidean domain, Euclidean division allows defining a Euclidean algorithm for computing greatest common divisors. However this does not imply the existence of a factorization algorithm. There is an explicit example of a field F such that there cannot exist any factorization algorithm in the Euclidean domain F[x] of the univariate polynomials over F.

Ideals

Main article: Dedekind domain

In algebraic number theory, the study of Diophantine equations led mathematicians, during 19th century, to introduce generalizations of the integers called algebraic integers. The first ring of algebraic integers that have been considered were Gaussian integers and Eisenstein integers, which share with usual integers the property of being principal ideal domains, and have thus the unique factorization property.

Unfortunately, it soon appeared that most rings of algebraic integers are not principal and do not have unique factorization. The simplest example is ${\displaystyle \mathbb{Z}[\sqrt{-5}],}$ in which

${\displaystyle 9=3\cdot 3=(2+\sqrt{-5})(2-\sqrt{-5}),}$

and all these factors are irreducible.

This lack of unique factorization is a major difficulty for solving Diophantine equations. For example, many wrong proofs of Fermat's Last Theorem (probably including Fermat's "truly marvelous proof of this, which this margin is too narrow to contain") were based on the implicit supposition of unique factorization.

This difficulty was resolved by Dedekind, who proved that the rings of algebraic integers have unique factorization of ideals: in these rings, every ideal is a product of prime ideals, and this factorization is unique up the order of the factors. The integral domains that have this unique factorization property are now called Dedekind domains. They have many nice properties that make them fundamental in algebraic number theory.

Matrices

Matrix rings are non-commutative and have no unique factorization: there are, in general, many ways of writing a matrix as a product of matrices. Thus, the factorization problem consists of finding factors of specified types. For example, the LU decomposition gives a matrix as the product of a lower triangular matrix by an upper triangular matrix. As this is not always possible, one generally considers the "LUP decomposition" having a permutation matrix as its third factor.

See Matrix decomposition for the most common types of matrix factorizations.

A logical matrix represents a binary relation, and matrix multiplication corresponds to composition of relations. Decomposition of a relation through factorization serves to profile the nature of the relation, such as a difunctional relation.

Actualism

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Actualism

In analytic philosophy, actualism is the view that everything there is (i.e., everything that has being, in the broadest sense) is actual. Another phrasing of the thesis is that the domain of unrestricted quantification ranges over all and only actual existents.

The denial of actualism is possibilism, the thesis that there are some entities that are merely possible: these entities have being but are not actual and, hence, enjoy a "less robust" sort of being than do actually existing things. An important, but significantly different notion of possibilism known as modal realism was developed by the philosopher David Lewis. On Lewis's account, the actual world is identified with the physical universe of which we are all a part. Other possible worlds exist in exactly the same sense as the actual world; they are simply spatio-temporally unrelated to our world, and to each other. Hence, for Lewis, "merely possible" entities—entities that exist in other possible worlds—exist in exactly the same sense as do we in the actual world; to be actual, from the perspective of any given individual x in any possible world, is simply to be part of the same world as x.

Actualists face the problem of explaining why many expressions commonly used in natural language are meaningful and sometimes even true despite the fact that they contain references to non-actual entities. Problematic expressions include names of fictional characters, definite descriptions and intentional attitude reports. Actualists have often responded to this problem by paraphrasing the expressions with apparently problematic ontological commitments into ones that are free of such commitments. Actualism has been challenged by truthmaker theory to explain how truths about what is possible or necessary depend on actuality, i.e. to point out which actual entities can act as truthmakers for them. Popular candidates for this role within an actualist ontology include possible worlds conceived as abstract objects, essences and dispositions.

Actualism and possibilism in ethics are two different theories about how future choices affect what the agent should presently do. Actualists assert that it is only relevant what the agent would actually do later for assessing the normative status of an alternative. Possibilists, on the other hand, hold that we should also take into account what the agent could do, even if he wouldn't do it.

Example

Consider the statement "Sherlock Holmes exists." This is a false statement about the world, but is usually accepted as representing a possible truth. This contingency is usually described by the statement "there is a possible world in which Sherlock Holmes exists". The possibilist argues that apparent existential claims such as this (that "there are" possible worlds of various sorts) ought to be taken more or less at face value: as stating the existence of two or more worlds, only one of which (at the most) can be the actual one. Hence, they argue, there are innumerably many possible worlds other than our own, which exist just as much as ours does.

Most actualists will be happy to grant the interpretation of "Sherlock Holmes' existence is possible" in terms of possible worlds. But they argue that the possibilist goes wrong in taking this as a sign that there exist other worlds that are just like ours, except for the fact that we are not actually in them. The actualist argues, instead, that when we claim "possible worlds" exist we are making claims that things exist in our own actual world which can serve as possible worlds for the interpretation of modal claims: that many ways the world could be (actually) exist, but not that any worlds which are those ways exist other than the actual world around us.

Viewpoints

From an actualist point of view, such as Adams', possible worlds are nothing more than fictions created within the actual world. Possible worlds are mere descriptions of ways this world (the actual one) might have been, and nothing else. Thus, as modal constructions, they come in as a handy heuristic device to use with modal logic; as it helps our modal reasoning to imagine ways the world might have been. Thus, the actualist interpretation of "◊p" sees the modality (i.e., "the way" in which it is true) as being de dicto and not entailing any ontological commitment.

So, from this point of view, what distinguishes the actual world from other possible worlds is what distinguishes reality from a description of a simulation of reality, this world from Sherlock Holmes': the former exists and is not a product of imagination and the latter does not exist and is a product of the imagination set in a modal construction.

From a modal realist's point of view, such as Lewis', the proposition "◊p" means that p obtains in at least one other, distinct world that is as real as the one we are in. If a state of affairs is possible, then it really obtains, it physically occurs in at least one world. Therefore, as Lewis is happy to admit, there is a world where someone named Sherlock Holmes lived at 221b Baker Street in Victorian times, there is another world where pigs fly, and there is even another world where both Sherlock Holmes exists and pigs fly.

This leaves open the question, of course, of what an actually existing "way the world could be" is; and on this question actualists are divided. One of the most popular solutions is to claim, as William Lycan and Robert Adams do, that "possible worlds" talk can be reduced to logical relations amongst consistent and maximally complete sets of propositions. "Consistent" here means that none of its propositions contradict one another (if they did, it would not be a possible description of the world); "maximally complete" means that the set covers every feature of the world. (More precisely: a set of propositions is "maximally complete" if, for any meaningful proposition P, P is either an element of the set, or the negation of an element of the set, or entailed by the conjunction of one or more elements of the set, or the negation of a proposition entailed by the conjunction of one or more elements of the set). Here the "possible world" which is said to be actual is actual in virtue of all its elements being true of the world around us.

Another common actualist account, advanced in different forms by Alvin Plantinga and David Armstrong, views "possible worlds" not as descriptions of how the world might be (through a very large set of statements) but rather as a maximally complete state of affairs that covers every state of affairs which might obtain or not obtain. Here, the "possible world" which is said to be actual is actual in virtue of that state of affairs obtaining in the world around us (since it is maximally complete, only one such state of affairs could actually obtain; all the others would differ from the actual world in various large or small ways).

Language and non-actual objects

Actualism, the view that being is restricted to actual being, is usually contrasted with possibilism, the view that being also includes possible entities, so-called possibilia. But there is a third and even wider-ranging view, Meinongianism, which holds that being includes impossible entities. So actualists disagree with both possibilists and Meinongians whether there are possible objects, e.g. unicorns, while actualists and possibilists disagree with Meinongians whether there are impossible objects, e.g. round squares.

The disagreements between these three views touch many areas in philosophy, including the semantics of natural language and the problem of intentionality. This is due to the fact that various expressions commonly used in natural language seem to refer to merely possible and in some cases even impossible objects. Since actualists deny the existence of such objects, it would seem that they are committed to the view that these expressions don't refer to anything and are therefore meaningless. This would be a rather unintuitive consequence of actualism, which is why actualists have proposed different strategies for different types of expressions in order to avoid this conclusion. These strategies usually involve some kind of paraphrase that transforms a sentence with apparently problematic ontological commitments into one that is free of such commitments.

Names and definite descriptions

Names of non-existent entities, like the 'planet' Vulcan, or names of fictional characters, like Sherlock Holmes, are one type of problematic expressions. These expressions are usually considered meaningful despite the fact that neither Vulcan nor Sherlock Holmes have actual existence. Similar cases come from definite descriptions that fail to refer, like "the present king of France". Possibilists and Meinongians have no problem to account for the meaning of these expressions: they just refer to possible objects. (Possibilists share this problem with the actualists in case of definite descriptions involving impossibility like "the round square") A widely known solution to these problems comes from Bertrand Russell. He proposed to analyze both names and definite descriptions in terms of quantified expressions. For example, the expression "The present king of France is bald" could be paraphrased as "there is exactly one thing that is currently king of France, and all such things are bald". This sentence is false, but it doesn't contain a reference to any non-actual entities anymore, thanks to the paraphrase. So the actualist has solved the problem of accounting for its meaning.

Intentional attitude reports

Intentional attitude reports about non-actual entities are another type of problematic cases, for example "Peter likes Superman". Possibilists can interpret the intentional attitude, in this case the liking, as a relation between Peter, an actual person, and Superman, a possible person. One actualist solution to this problem involves treating intentional attitudes not as relations between a subject and an object but as properties of the subject. This approach has been termed "adverbialism" since the object of the intentional attitude is seen as a modification of the attitude: "Peter likes superman-ly". This paraphrase succeeds in removing any reference to non-actual entities.

Truthmaker theory and modal truths

Truthmaker theorists hold that truth depends on reality. In the terms of truthmaker theory: a truthbearer (e.g. a proposition) is true because of the existence of its truthmaker (e.g. a fact). Positing a truth without being able to account for its truthmaker violates this principle and has been labeled "ontological cheating". Actualists face the problem of how to account for the truthmakers of modal truths, like "it was possible for the Cuban Missile Crisis to escalate into a full-scale nuclear war", "there could have been purple cows" or "it is necessary that all cows are animals". Actualists have proposed various solutions, but there is no consensus as to which one is the best solution.

Possible worlds

A well-known account relies on the notion of possible worlds, conceived as actual abstract objects, for example as maximal consistent sets of propositions or of states of affairs. A set of propositions is maximal if, for any statement p, either p or not-p is a member. Possible worlds act as truthmakers for modal truths. For example, there is a possible world which is inhabited by purple cows. This world is a truthmaker for "there could have been purple cows". Cows are animals in all possible worlds that are inhabited by cows. So all worlds are the truthmaker of "it is necessary that all cows are animals". This account relies heavily on a logical notion of modality, since possibility and necessity are defined in terms of consistency. This dependency has prompted some philosophers to assert that no truthmakers at all are needed for modal truths, that modal truths are true "by default". This position involves abandoning truthmaker maximalism.

Essences

An alternative solution to the problem of truthmakers for modal truths is based on the notion of essence. Objects have their properties either essentially or accidentally. The essence of an object involves all the properties it has essentially; it defines the object's nature: what it fundamentally is. On this type of account, the truthmaker for "it is necessary that all cows are animals" is that it belongs to the essence of cows to be animals. The truthmaker for "there could have been purple cows" is that color is not essential to cows. Some essentialist theories focus on object essences, i.e. that certain properties are essential to a specific object. Other essentialist theories focus on kind essences, i.e. that certain properties are essential to the kind or species of the object in question.

Dispositions

Another account attempts to ground modal truths in the dispositions or powers of actually existing entities. So, for example, the claim that "it's possible that the teacup breaks" has its truthmaker in the teacup's disposition to break, i.e. in its fragility. While this type of theory can account for various truths, it has been questioned whether it can account for all truths. Problematic cases include truths like "it's possible that nothing existed" or "it's possible that the laws of nature had been different". A theistic version of this account has been proposed in order to solve these problems: God's power is the truthmaker for modal truths. "There could have been purple cows" because it was in God's power to create purple cows, while "it is necessary that all cows are animals" because it was not in God's power to create cows that are not animals.

Softcore vs hardcore

These solutions proposed on behalf of actualism can be divided into two categories: Softcore actualism and hardcore actualism. The adherents of these positions disagree on which part of the actual world is the foundation supporting modal truths. Softcore actualists hold that modal truths are grounded in the abstract realm, for example in possible worlds conceived as abstract objects existing in the actual world. Hardcore actualists, on the other hand, assert that modal truths are grounded in the concrete constituents of the actual world, for example in essences or in dispositions.

Indexical actuality analysis

According to the indexical conception of actuality, favoured by Lewis (1986), actuality is an attribute which our world has relative to itself, but which all the other worlds have relative to themselves too. Actuality is an intrinsic property of each world, so world w is actual just at world w. "Actual" is seen as an indexical term, and its reference depends on its context. Therefore, there is no feature of this world (nor of any other) to be distinguished in order to infer that the world is actual, "the actual world" is actual simply in virtue of the definition of "actual": a world is actual simpliciter.

Ethics

Actualism and possibilism in ethics are, in contrast to the main part of this article, not concerned with metaphysical claims. Instead, their goal, as ethical theories, is to determine what one ought to do. They are mostly, but not exclusively, relevant for consequentialism, the theory that an action is right if and only if its consequences are better than the consequences of any alternative action. These consequences may include other actions of the agent at a later point in time. Actualists assert that it is only relevant what the agent would actually do later for assessing the value of an alternative. Possibilists, on the other hand, hold that we should also take into account what the agent could do, even if she wouldn't do it.

For example, assume that Gifre has the choice between two alternatives, eating a cookie or not eating anything. Having eaten the first cookie, Gifre could stop eating cookies, which is the best alternative. But after having tasted one cookie, Gifre would freely decide to continue eating cookies until the whole bag is finished, which would result in a terrible stomach ache and would be the worst alternative. Not eating any cookies at all, on the other hand, would be the second-best alternative. Now the question is: should Gifre eat the first cookie or not? Actualists are only concerned with the actual consequences. According to them, Gifre should not eat any cookies at all since it is better than the alternative leading to a stomach ache. Possibilists contend that the best possible course of action involves eating the first cookie and this is therefore what Gifre should do.

One counterintuitive consequence of actualism is that agents can avoid moral obligations simply by having an imperfect moral character. For example, a lazy person might justify rejecting a request to help a friend by arguing that, due to her lazy character, she wouldn't have done the work anyway, even if she had accepted the request. By rejecting the offer right away, she managed at least not to waste anyone's time. Actualists might even consider her behavior praiseworthy since she did what, according to actualism, she ought to have done. This seems to be a very easy way to "get off the hook" that is avoided by possibilism. But possibilism has to face the objection that in some cases it sanctions and even recommends what actually leads to the worst outcome.

Douglas W. Portmore has suggested that these and other problems of actualism and possibilism can be avoided by constraining what counts as a genuine alternative for the agent. On his view, it is a requirement that the agent has rational control over the event in question. For example, eating only one cookie and stopping afterward only is an option for Gifre if she has the rational capacity to repress her temptation to continue eating. If the temptation is irrepressible then this course of action is not considered to be an option and is therefore not relevant when assessing what the best alternative is. Portmore suggests that, given this adjustment, we should prefer a view very closely associated with possibilism called maximalism.