Time dilation

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Time_dilation

 

Time dilation is the difference in elapsed time as measured by two clocks, either because of a relative velocity between them (special relativity), or a difference in gravitational potential between their locations (general relativity). When unspecified, "time dilation" usually refers to the effect due to velocity.

After compensating for varying signal delays resulting from the changing distance between an observer and a moving clock (i.e. Doppler effect), the observer will measure the moving clock as ticking more slowly than a clock at rest in the observer's own reference frame. In addition, a clock that is close to a massive body (and which therefore is at lower gravitational potential) will record less elapsed time than a clock situated farther from the same massive body (and which is at a higher gravitational potential).

These predictions of the theory of relativity have been repeatedly confirmed by experiment, and they are of practical concern, for instance in the operation of satellite navigation systems such as GPS and Galileo.

History

Main article: History of special relativity

Time dilation by the Lorentz factor was predicted by several authors at the turn of the 20th century. Joseph Larmor (1897) wrote that, at least for those orbiting a nucleus, individual electrons describe corresponding parts of their orbits in times shorter for the [rest] system in the ratio: $\sqrt{1-\frac{v^2}{c^2}}$. Emil Cohn (1904) specifically related this formula to the rate of clocks. In the context of special relativity it was shown by Albert Einstein (1905) that this effect concerns the nature of time itself, and he was also the first to point out its reciprocity or symmetry. Subsequently, Hermann Minkowski (1907) introduced the concept of proper time which further clarified the meaning of time dilation.

Time dilation caused by a relative velocity

See also: Special relativity § Time dilation

From the local frame of reference of the blue clock, the red clock, being in motion, is perceived as ticking slower.

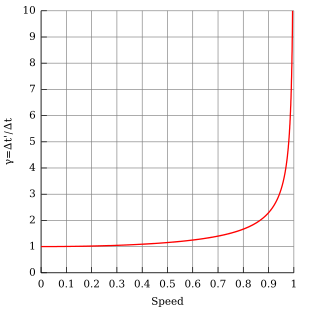
Special relativity indicates that, for an observer in an inertial frame of reference, a clock that is moving relative to the observer will be measured to tick slower than a clock at rest in the observer's frame of reference. This is sometimes called special relativistic time dilation. The faster the relative velocity, the greater the time dilation between them, with time slowing to a stop as one clock approaches the speed of light (299,792,458 m/s).

In theory, time dilation would make it possible for passengers in a fast-moving vehicle to advance into the future in a short period of their own time. With sufficiently high speeds, the effect would be dramatic. For example, one year of travel might correspond to ten years on Earth. Indeed, a constant 1 g acceleration would permit humans to travel through the entire known Universe in one human lifetime.

With current technology severely limiting the velocity of space travel, the differences experienced in practice are minuscule. After 6 months on the International Space Station (ISS), orbiting Earth at a speed of about 7,700 m/s, an astronaut would have aged about 0.005 seconds less than he would have on Earth. The cosmonauts Sergei Krikalev and Sergei Avdeyev both experienced time dilation of about 20 milliseconds compared to time that passed on Earth.

Simple inference

Left: Observer at rest measures time 2L/c between co-local events of light signal generation at A and arrival at A.
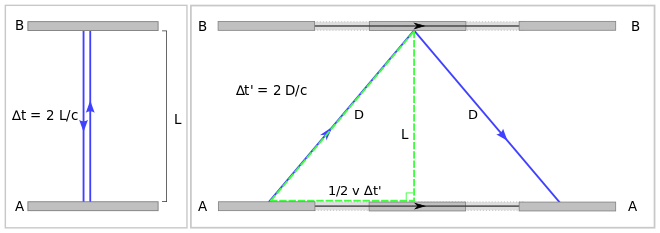
Right: Events according to an observer moving to the left of the setup: bottom mirror A when signal is generated at time t'=0, top mirror B when signal gets reflected at time t'=D/c, bottom mirror A when signal returns at time t'=2D/c

Time dilation can be inferred from the observed constancy of the speed of light in all reference frames dictated by the second postulate of special relativity. This constancy of the speed of light means that, counter to intuition, the speeds of material objects and light are not additive. It is not possible to make the speed of light appear greater by moving towards or away from the light source.

Consider then, a simple vertical clock consisting of two mirrors A and B, between which a light pulse is bouncing. The separation of the mirrors is L and the clock ticks once each time the light pulse hits mirror A.

In the frame in which the clock is at rest (see left part of the diagram), the light pulse traces out a path of length 2L and the time period between the ticks of the clock ${\displaystyle \mathrm{\Delta }t}$ is equal to 2L divided by the speed of light c:

${\displaystyle \mathrm{\Delta }t=\frac{2L}{c}}$

From the frame of reference of a moving observer traveling at the speed v relative to the resting frame of the clock (right part of diagram), the light pulse is seen as tracing out a longer, angled path 2D. Keeping the speed of light constant for all inertial observers requires a lengthening (that is dilation) of the time period between the ticks of this clock ${\displaystyle \mathrm{\Delta }{t}^{\prime }}$ from the moving observer's perspective. That is to say, as measured in a frame moving relative to the local clock, this clock will be running (that is ticking) more slowly, since tick rate equals one over the time period between ticks 1/${\displaystyle \mathrm{\Delta }{t}^{\prime }}$.

Straightforward application of the Pythagorean theorem leads to the well-known prediction of special relativity:

The total time for the light pulse to trace its path is given by:

${\displaystyle \mathrm{\Delta }{t}^{\prime }=\frac{2D}{c}}$

The length of the half path can be calculated as a function of known quantities as:

${\displaystyle D=\sqrt{{\left(\frac{1}{2}v\mathrm{\Delta }{t}^{\prime }\right)}^2+L^2}}$

Elimination of the variables D and L from these three equations results in:

Time dilation equation

${\displaystyle \mathrm{\Delta }{t}^{\prime }=\frac{\mathrm{\Delta }t}{\sqrt{1-\frac{v^2}{c^2}}}=\gamma \mathrm{\Delta }t}$

which expresses the fact that the moving observer's period of the clock ${\displaystyle \mathrm{\Delta }{t}^{\prime }}$ is longer than the period ${\displaystyle \mathrm{\Delta }t}$ in the frame of the clock itself. The Lorentz factor gamma (γ) is defined as

${\displaystyle \gamma =\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}$

Because all clocks that have a common period in the resting frame should have a common period when observed from the moving frame, all other clocks—mechanical, electronic, optical (such as an identical horizontal version of the clock in the example)—should exhibit the same velocity-dependent time dilation.

Reciprocity

Transversal time dilation. The blue dots represent a pulse of light. Each pair of dots with light "bouncing" between them is a clock. In the frame of each group of clocks, the other group is measured to tick more slowly, because the moving clock's light pulse has to travel a larger distance than the stationary clock's light pulse. That is so, even though the clocks are identical and their relative motion is perfectly reciprocal.

Given a certain frame of reference, and the "stationary" observer described earlier, if a second observer accompanied the "moving" clock, each of the observers would perceive the other's clock as ticking at a slower rate than their own local clock, due to them both perceiving the other to be the one that is in motion relative to their own stationary frame of reference.

Common sense would dictate that, if the passage of time has slowed for a moving object, said object would observe the external world's time to be correspondingly sped up. Counterintuitively, special relativity predicts the opposite. When two observers are in motion relative to each other, each will measure the other's clock slowing down, in concordance with them being in motion relative to the observer's frame of reference.

Time UV of a clock in S is shorter compared to Ux′ in S′, and time UW of a clock in S′ is shorter compared to Ux in S.

While this seems self-contradictory, a similar oddity occurs in everyday life. If two persons A and B observe each other from a distance, B will appear small to A, but at the same time, A will appear small to B. Being familiar with the effects of perspective, there is no contradiction or paradox in this situation.

The reciprocity of the phenomenon also leads to the so-called twin paradox where the aging of twins, one staying on Earth and the other embarking on space travel, is compared, and where the reciprocity suggests that both persons should have the same age when they reunite. On the contrary, at the end of the round-trip, the traveling twin will be younger than the sibling on Earth. The dilemma posed by the paradox can be explained by the fact that situation is not symmetric. The twin staying on Earth is in a single inertial frame, and the traveling twin is in two different inertial frames: one on the way out and another on the way back. See also Twin paradox#Role of acceleration.

Experimental testing

Main article: Experimental testing of time dilation

See also: Tests of special relativity

Moving particles

• A comparison of muon lifetimes at different speeds is possible. In the laboratory, slow muons are produced; and in the atmosphere, very fast-moving muons are introduced by cosmic rays. Taking the muon lifetime at rest as the laboratory value of 2.197 μs, the lifetime of a cosmic-ray-produced muon traveling at 98% of the speed of light is about five times longer, in agreement with observations. An example is Rossi and Hall (1941), who compared the population of cosmic-ray-produced muons at the top of a mountain to that observed at sea level.
• The lifetime of particles produced in particle accelerators are longer due to time dilation. In such experiments, the "clock" is the time taken by processes leading to muon decay, and these processes take place in the moving muon at its own "clock rate", which is much slower than the laboratory clock. This is routinely taken into account in particle physics, and many dedicated measurements have been performed. For instance, in the muon storage ring at CERN the lifetime of muons circulating with γ = 29.327 was found to be dilated to 64.378 μs, confirming time dilation to an accuracy of 0.9 ± 0.4 parts per thousand.

Doppler effect

Main article: Ives–Stilwell experiment

• The stated purpose by Ives and Stilwell (1938, 1941) of these experiments was to verify the time dilation effect, predicted by Larmor–Lorentz ether theory, due to motion through the ether using Einstein's suggestion that Doppler effect in canal rays would provide a suitable experiment. These experiments measured the Doppler shift of the radiation emitted from cathode rays, when viewed from directly in front and from directly behind. The high and low frequencies detected were not the classically predicted values:
  $${\displaystyle \frac{f_0}{1-v/c}\text{and}\frac{f_0}{1+v/c}}$$

  
  The high and low frequencies of the radiation from the moving sources were measured as:
  $${\displaystyle \sqrt{\frac{1+v/c}{1-v/c}}{f}_0=\gamma \left(1+v/c\right)f_0\text{and}\sqrt{\frac{1-v/c}{1+v/c}}{f}_0=\gamma \left(1-v/c\right)f_0}$$

  
  as deduced by Einstein (1905) from the Lorentz transformation, when the source is running slow by the Lorentz factor.
• Hasselkamp, Mondry, and Scharmann (1979) measured the Doppler shift from a source moving at right angles to the line of sight. The most general relationship between frequencies of the radiation from the moving sources is given by:
  $${\displaystyle f_{\mathrm{d}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}}=f_{\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}}\left(1-\frac{v}{c}\cos \varphi \right)/\sqrt{1-v^2/c^2}}$$

  
  as deduced by Einstein (1905). For ϕ = 90° (cos ϕ = 0) this reduces to f_detected = f_restγ. This lower frequency from the moving source can be attributed to the time dilation effect and is often called the transverse Doppler effect and was predicted by relativity.
• In 2010 time dilation was observed at speeds of less than 10 metres per second using optical atomic clocks connected by 75 metres of optical fiber.

Proper time and Minkowski diagram

Minkowski diagram and twin paradox

Clock C in relative motion between two synchronized clocks A and B. C meets A at d, and B at f.

 

Twin paradox. One twin has to change frames, leading to different proper times in the twin's world lines.

In the Minkowski diagram from the first image on the right, clock C resting in inertial frame S′ meets clock A at d and clock B at f (both resting in S). All three clocks simultaneously start to tick in S. The worldline of A is the ct-axis, the worldline of B intersecting f is parallel to the ct-axis, and the worldline of C is the ct′-axis. All events simultaneous with d in S are on the x-axis, in S′ on the x′-axis.

The proper time between two events is indicated by a clock present at both events. It is invariant, i.e., in all inertial frames it is agreed that this time is indicated by that clock. Interval df is, therefore, the proper time of clock C, and is shorter with respect to the coordinate times ef=dg of clocks B and A in S. Conversely, also proper time ef of B is shorter with respect to time if in S′, because event e was measured in S′ already at time i due to relativity of simultaneity, long before C started to tick.

From that it can be seen, that the proper time between two events indicated by an unaccelerated clock present at both events, compared with the synchronized coordinate time measured in all other inertial frames, is always the minimal time interval between those events. However, the interval between two events can also correspond to the proper time of accelerated clocks present at both events. Under all possible proper times between two events, the proper time of the unaccelerated clock is maximal, which is the solution to the twin paradox.

Derivation and formulation

Lorentz factor as a function of speed (in natural units where c = 1). Notice that for small speeds (as v tends to zero), γ is approximately 1.

In addition to the light clock used above, the formula for time dilation can be more generally derived from the temporal part of the Lorentz transformation. Let there be two events at which the moving clock indicates ${\displaystyle t_a}$ and ${\displaystyle t_b}$, thus:

${\displaystyle t_a^{\mathrm{\prime }}=\frac{t_a-\frac{v{x}_a}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}},t_b^{\mathrm{\prime }}=\frac{t_b-\frac{v{x}_b}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}}$

Since the clock remains at rest in its inertial frame, it follows ${\displaystyle x_a=x_b}$, thus the interval ${\displaystyle \mathrm{\Delta }{t}^{\mathrm{\prime }}=t_b^{\mathrm{\prime }}-t_a^{\mathrm{\prime }}}$ is given by:

${\displaystyle \mathrm{\Delta }{t}^{\prime }=\gamma \mathrm{\Delta }t=\frac{\mathrm{\Delta }t}{\sqrt{1-\frac{v^2}{c^2}}}}$

where Δt is the time interval between two co-local events (i.e. happening at the same place) for an observer in some inertial frame (e.g. ticks on their clock), known as the proper time, Δt′ is the time interval between those same events, as measured by another observer, inertially moving with velocity v with respect to the former observer, v is the relative velocity between the observer and the moving clock, c is the speed of light, and the Lorentz factor (conventionally denoted by the Greek letter gamma or γ) is:

${\displaystyle \gamma =\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}$

Thus the duration of the clock cycle of a moving clock is found to be increased: it is measured to be "running slow". The range of such variances in ordinary life, where v ≪ c, even considering space travel, are not great enough to produce easily detectable time dilation effects and such vanishingly small effects can be safely ignored for most purposes. As an approximate threshold, time dilation may become important when an object approaches speeds on the order of 30,000 km/s (1/10 the speed of light).

Hyperbolic motion

Main article: Hyperbolic motion (relativity)

In special relativity, time dilation is most simply described in circumstances where relative velocity is unchanging. Nevertheless, the Lorentz equations allow one to calculate proper time and movement in space for the simple case of a spaceship which is applied with a force per unit mass, relative to some reference object in uniform (i.e. constant velocity) motion, equal to g throughout the period of measurement.

Let t be the time in an inertial frame subsequently called the rest frame. Let x be a spatial coordinate, and let the direction of the constant acceleration as well as the spaceship's velocity (relative to the rest frame) be parallel to the x-axis. Assuming the spaceship's position at time t = 0 being x = 0 and the velocity being v₀ and defining the following abbreviation:

${\displaystyle {\gamma }_0=\frac{1}{\sqrt{1-v_0^2/c^2}}}$

the following formulas hold:

Position:

${\displaystyle x(t)=\frac{c^2}{g}\left(\sqrt{1+\frac{{\left(gt+v_0{\gamma }_0\right)}^2}{c^2}}-{\gamma }_0\right)}$

Velocity:

${\displaystyle v(t)=\frac{gt+v_0{\gamma }_0}{\sqrt{1+\frac{{\left(gt+v_0{\gamma }_0\right)}^2}{c^2}}}}$

Proper time as function of coordinate time:

${\displaystyle \tau (t)={\tau }_0+{\int }_0^t\sqrt{1-{\left(\frac{v(t^{\prime })}{c}\right)}^2}d{t}^{\prime }}$

In the case where v(0) = v₀ = 0 and τ(0) = τ₀ = 0 the integral can be expressed as a logarithmic function or, equivalently, as an inverse hyperbolic function:

${\displaystyle \tau (t)=\frac{c}{g}\ln \left(\frac{gt}{c}+\sqrt{1+{\left(\frac{gt}{c}\right)}^2}\right)=\frac{c}{g}\mathrm{arsinh}\left(\frac{gt}{c}\right)}$

As functions of the proper time ${\displaystyle \tau }$ of the ship, the following formulae hold:

Position:

${\displaystyle x(\tau )=\frac{c^2}{g}\left(\cosh \frac{g\tau }{c}-1\right)}$

Velocity:

${\displaystyle v(\tau )=c\tanh \frac{g\tau }{c}}$

Coordinate time as function of proper time:

${\displaystyle t(\tau )=\frac{c}{g}\sinh \frac{g\tau }{c}}$

Clock hypothesis

The clock hypothesis is the assumption that the rate at which a clock is affected by time dilation does not depend on its acceleration but only on its instantaneous velocity. This is equivalent to stating that a clock moving along a path ${\displaystyle P}$ measures the proper time, defined by:

${\displaystyle \tau ={\int }_P\sqrt{d{t}^2-d{x}^2/c^2-d{y}^2/c^2-d{z}^2/c^2}}$

The clock hypothesis was implicitly (but not explicitly) included in Einstein's original 1905 formulation of special relativity. Since then, it has become a standard assumption and is usually included in the axioms of special relativity, especially in light of experimental verification up to very high accelerations in particle accelerators.

Time dilation caused by gravity or acceleration

Main article: Gravitational time dilation

Time dilation explains why two working clocks will report different times after different accelerations. For example, time goes slower at the ISS, lagging approximately 0.01 seconds for every 12 Earth months passed. For GPS satellites to work, they must adjust for similar bending of spacetime to coordinate properly with systems on Earth.

Time passes more quickly further from a center of gravity, as is witnessed with massive objects (like the Earth).

Gravitational time dilation is experienced by an observer that, at a certain altitude within a gravitational potential well, finds that their local clocks measure less elapsed time than identical clocks situated at higher altitude (and which are therefore at higher gravitational potential).

Gravitational time dilation is at play e.g. for ISS astronauts. While the astronauts' relative velocity slows down their time, the reduced gravitational influence at their location speeds it up, although to a lesser degree. Also, a climber's time is theoretically passing slightly faster at the top of a mountain compared to people at sea level. It has also been calculated that due to time dilation, the core of the Earth is 2.5 years younger than the crust. "A clock used to time a full rotation of the Earth will measure the day to be approximately an extra 10 ns/day longer for every km of altitude above the reference geoid." Travel to regions of space where extreme gravitational time dilation is taking place, such as near (but not beyond the event horizon of) a black hole, could yield time-shifting results analogous to those of near-lightspeed space travel.

Contrarily to velocity time dilation, in which both observers measure the other as aging slower (a reciprocal effect), gravitational time dilation is not reciprocal. This means that with gravitational time dilation both observers agree that the clock nearer the center of the gravitational field is slower in rate, and they agree on the ratio of the difference.

Experimental testing

Main article: Experimental testing of time dilation

• In 1959, Robert Pound and Glen A. Rebka measured the very slight gravitational redshift in the frequency of light emitted at a lower height, where Earth's gravitational field is relatively more intense. The results were within 10% of the predictions of general relativity. In 1964, Pound and J. L. Snider measured a result within 1% of the value predicted by gravitational time dilation. (See Pound–Rebka experiment)
• In 2010, gravitational time dilation was measured at the Earth's surface with a height difference of only one meter, using optical atomic clocks.

Combined effect of velocity and gravitational time dilation

Daily time dilation (gain or loss if negative) in microseconds as a function of (circular) orbit radius r = rs/re, where rs is satellite orbit radius and re is the equatorial Earth radius, calculated using the Schwarzschild metric. At r ≈ 1.497^{[Note 1]} there is no time dilation. Here the effects of motion and reduced gravity cancel. ISS astronauts fly below, whereas GPS and geostationary satellites fly above.

High-accuracy timekeeping, low-Earth-orbit satellite tracking, and pulsar timing are applications that require the consideration of the combined effects of mass and motion in producing time dilation. Practical examples include the International Atomic Time standard and its relationship with the Barycentric Coordinate Time standard used for interplanetary objects.

Relativistic time dilation effects for the solar system and the Earth can be modeled very precisely by the Schwarzschild solution to the Einstein field equations. In the Schwarzschild metric, the interval ${\displaystyle d{t}_{\text{E}}}$ is given by:

${\displaystyle d{t}_{\text{E}}^2=\left(1-\frac{2G{M}_{\text{i}}}{r_{\text{i}}{c}^2}\right)d{t}_{\text{c}}^2-{\left(1-\frac{2G{M}_{\text{i}}}{r_{\text{i}}{c}^2}\right)}^{-1}\frac{d{x}^2+d{y}^2+d{z}^2}{c^2}}$

where:

• ${\displaystyle d{t}_{\text{E}}}$ is a small increment of proper time ${\displaystyle t_{\text{E}}}$ (an interval that could be recorded on an atomic clock),
• ${\displaystyle d{t}_{\text{c}}}$ is a small increment in the coordinate ${\displaystyle t_{\text{c}}}$ (coordinate time),
• ${\displaystyle dx,dy,dz}$ are small increments in the three coordinates ${\displaystyle x,y,z}$ of the clock's position,
• ${\displaystyle \frac{-G{M}_i}{r_i}}$ represents the sum of the Newtonian gravitational potentials due to the masses in the neighborhood, based on their distances ${\displaystyle r_i}$ from the clock. This sum includes any tidal potentials.

The coordinate velocity of the clock is given by:

${\displaystyle v^2=\frac{d{x}^2+d{y}^2+d{z}^2}{d{t}_{\text{c}}^2}}$

The coordinate time ${\displaystyle t_c}$ is the time that would be read on a hypothetical "coordinate clock" situated infinitely far from all gravitational masses (${\displaystyle U=0}$), and stationary in the system of coordinates (${\displaystyle v=0}$). The exact relation between the rate of proper time and the rate of coordinate time for a clock with a radial component of velocity is:

${\displaystyle \frac{d{t}_{\text{E}}}{d{t}_{\text{c}}}=\sqrt{1+\frac{2U}{c^2}-\frac{v^2}{c^2}+{\left(\frac{c^2}{2U}+1\right)}^{-1}\frac{{v_{\parallel }}^2}{c^2}}=\sqrt{1-\left({\beta }^2+{\beta }_e^2+\frac{{\beta }_{\parallel }^2{\beta }_e^2}{1-{\beta }_e^2}\right)}}$

where:

• ${\displaystyle v_{\parallel }}$ is the radial velocity,
• ${\displaystyle v_e=\sqrt{\frac{2G{M}_i}{r_i}}}$ is the escape speed,
• ${\displaystyle \beta =v/c}$, ${\displaystyle {\beta }_e=v_e/c}$ and ${\displaystyle {\beta }_{\parallel }=v_{\parallel }/c}$ are velocities as a percentage of speed of light c,
• ${\displaystyle U=\frac{-G{M}_i}{r_i}}$ is the Newtonian potential; hence ${\displaystyle -U}$ equals half the square of the escape speed.

The above equation is exact under the assumptions of the Schwarzschild solution. It reduces to velocity time dilation equation in the presence of motion and absence of gravity, i.e. ${\displaystyle {\beta }_e=0}$. It reduces to gravitational time dilation equation in the absence of motion and presence of gravity, i.e. ${\displaystyle \beta =0={\beta }_{\parallel }}$.

Experimental testing

Daily time dilation over circular orbit height split into its components. On this chart, only Gravity Probe A was launched specifically to test general relativity. The other spacecraft on this chart (except for the ISS, whose range of points is marked "theory") carry atomic clocks whose proper operation depend on the validity of general relativity.

• Hafele and Keating, in 1971, flew caesium atomic clocks east and west around the Earth in commercial airliners, to compare the elapsed time against that of a clock that remained at the U.S. Naval Observatory. Two opposite effects came into play. The clocks were expected to age more quickly (show a larger elapsed time) than the reference clock since they were in a higher (weaker) gravitational potential for most of the trip (c.f. Pound–Rebka experiment). But also, contrastingly, the moving clocks were expected to age more slowly because of the speed of their travel. From the actual flight paths of each trip, the theory predicted that the flying clocks, compared with reference clocks at the U.S. Naval Observatory, should have lost 40±23 nanoseconds during the eastward trip and should have gained 275±21 nanoseconds during the westward trip. Relative to the atomic time scale of the U.S. Naval Observatory, the flying clocks lost 59±10 nanoseconds during the eastward trip and gained 273±7 nanoseconds during the westward trip (where the error bars represent standard deviation). In 2005, the National Physical Laboratory in the United Kingdom reported their limited replication of this experiment. The NPL experiment differed from the original in that the caesium clocks were sent on a shorter trip (London–Washington, D.C. return), but the clocks were more accurate. The reported results are within 4% of the predictions of relativity, within the uncertainty of the measurements.
• The Global Positioning System can be considered a continuously operating experiment in both special and general relativity. The in-orbit clocks are corrected for both special and general relativistic time dilation effects as described above, so that (as observed from the Earth's surface) they run at the same rate as clocks on the surface of the Earth.

In popular culture

Velocity and gravitational time dilation have been the subject of science fiction works in a variety of media. Some examples in film are the movies Interstellar and Planet of the Apes. In Interstellar, a key plot point involves a planet, which is close to a rotating black hole and on the surface of which one hour is equivalent to seven years on Earth due to time dilation. Physicist Kip Thorne collaborated in making the film and explained its scientific concepts in the book The Science of Interstellar.

Time dilation was used in the Doctor Who episodes "World Enough and Time" and "The Doctor Falls", which take place on a spaceship in the vicinity of a black hole. Due to the immense gravitational pull of the black hole and the ship's length (400 miles), time moves faster at one end than the other. When The Doctor's companion, Bill, gets taken away to the other end of the ship, she waits years for him to rescue her; in his time, only minutes pass. Furthermore, the dilation allows the Cybermen to evolve at a "faster" rate than previously seen in the show.

Tau Zero, a novel by Poul Anderson, is an early example of the concept in science fiction literature. In the novel, a spacecraft uses a Bussard ramjet to accelerate to high enough speeds that the crew spends five years on board, but thirty-three years pass on the Earth before they arrive at their destination. The velocity time dilation is explained by Anderson in terms of the tau factor which decreases closer and closer to zero as the ship approaches the speed of light—hence the title of the novel. Due to an accident, the crew is unable to stop accelerating the spacecraft, causing such extreme time dilation that the crew experiences the Big Crunch at the end of the universe. Other examples in literature, such as Rocannon's World, Hyperion and The Forever War, similarly make use of relativistic time dilation as a scientifically plausible literary device to have certain characters age slower than the rest of the universe.

Light effects on circadian rhythm

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Light_effects_on_circadian_rhythm

Light effects on circadian rhythm are the effects that light has on circadian rhythm.

Most animals and other organisms have "built-in clocks" in their brains that regulate the timing of biological processes and daily behavior. These "clocks" are known as circadian rhythms. They allow maintenance of these processes and behaviors relative to the 24-hour day/night cycle in nature. Although these rhythms are maintained by the individual organisms, their length does vary somewhat individually. Therefore, they must, either continually or repeatedly, be reset to synchronize with nature's cycle. In order to maintain synchronization ("entrainment") to 24 hours, external factors must play some role. The human circadian rhythm occurs typically in accordance with nature's cycle. The average activity rhythm cycle is 24.18 hours in adulthood but is shortened as age increases. One of the various factors that influence this entrainment is light exposure to the eyes. When an organism is exposed to a specific wavelength of light stimulus at certain times throughout the day, the hormone melatonin is suppressed, or prevented from being secreted by the pineal gland.

Mechanism

Light first passes into a mammal's system through the retina, then takes one of two paths: the light gets collected by rod cells and cone cells and the retinal ganglion cells (RGCs), or it is directly collected by these RGCs.

The RGCs use the photopigment melanopsin to absorb the light energy. Specifically, this class of RGCs being discussed is referred to as "intrinsically photosensitive," which just means they are sensitive to light. There are five known types of intrinsically photosensitive retinal ganglion cells (ipRGCs): M1, M2, M3, M4, and M5. Each of these differently ipRGC types have different melanopsin content and photosensitivity. These connect to amacrine cells in the inner plexiform layer of the retina. Ultimately, via this retinohypothalamic tract (RHT) the suprachiasmatic nucleus (SCN) of the hypothalamus receives light information from these ipRGCs.

The ipRGCs serve a different function than rods and cones, even when isolated from the other components of the retina, ipRGCs maintain their photo-sensitivity and as a result can be sensitive to different ranges of the light spectrum. Additionally, ipRGC firing patterns may respond to light conditions as low as 1 lux whereas previous research indicated 2500 lux was required to suppress melatonin production. Circadian and other behavioral responses have shown to be more sensitive at lower wavelengths than the photopic luminous efficiency function which is based on sensitivity to cone receptors.

The core region of the SCN houses the majority of light-sensitive neurons. From here, signals are transmitted via a nerve connection with the pineal gland which regulates various hormones in the human body.

There are specific genes that determine the regulation of circadian rhythm in conjunction with light. When light activates NMDA receptors in the SCN, CLOCK gene expression in that region is altered and the SCN is reset, and this is how entrainment occurs. Genes also involved with entrainment are PER1 and PER2.

Some important structures directly impacted by the light-sleep relationship are the superior colliculus-pretectal area and the ventrolateral pre-optic nucleus.

The progressive yellowing of the crystalline lens with age reduces the amount of short-wavelength light reaching the retina and may contribute to circadian alterations observed in older adulthood.

Effects

Primary

All of the mechanisms of light-affected entrainment are not yet fully known, however numerous studies have demonstrated the effectiveness of light entrainment to the day/night cycle. Studies have shown that the timing of exposure to light influences entrainment; as seen on the phase response curve for light for a given species. In diurnal (day-active) species, exposure to light soon after wakening advances the circadian rhythm, whereas exposure before sleeping delays the rhythm. An advance means that the individual will tend to wake up earlier on the following day(s). A delay, caused by light exposure before sleeping, means that the individual will tend to wake up later on the following day(s).

The hormones cortisol and melatonin are affected by the signals light sends through the body's nervous system. These hormones help regulate blood sugar to give the body the appropriate amount of energy that is required throughout the day. Cortisol levels are high upon waking and gradually decrease over the course of the day, melatonin levels are high when the body is entering and exiting a sleeping status and are very low over the course of waking hours. The earth's natural light-dark cycle is the basis for the release of these hormones.

The length of light exposure influences entrainment. Longer exposures have a greater effect than shorter exposures. Consistent light exposure has a greater effect than intermittent exposure. In rats, constant light eventually disrupts the cycle to the point that memory and stress coping may be impaired.

The intensity and the wavelength of light influence entrainment. Dim light can affect entrainment relative to darkness. Brighter light is more effective than dim light. In humans, a lower intensity short wavelength (blue/violet) light appears to be equally effective as a higher intensity of white light.

Exposure to monochromatic light at the wavelengths of 460 nm and 550 nm on two control groups yielded results showing decreased sleepiness at 460 nm tested over two groups and a control group. Additionally, in the same study but testing thermoregulation and heart rate researchers found significantly increased heart rate in 460 nm light over the course of a 1.5 hour exposure period.

In a study done on the effect of lighting intensity on delta waves, a measure of sleepiness, high levels of lighting (1700 lux) showed lower levels of delta waves measured through an EEG than low levels of lighting (450 lux). This shows that lighting intensity is directly correlated with alertness in an office environment.

Humans are sensitive to light with a short wavelength. Specifically, melanopsin is sensitive to blue light with a wavelength of approximately 480 nanometers. The effect this wavelength of light has on melanopsin leads to physiological responses such as the suppression of melatonin production, increased alertness, and alterations to the circadian rhythm.

Secondary

While light has direct effects on circadian rhythm, there are indirect effects seen across studies. Seasonal affective disorder creates a model in which decreased day length during autumn and winter increases depressive symptoms. A shift in the circadian phase response curve creates a connection between the amount of light in a day (day length) and depressive symptoms in this disorder. Light seems to have therapeutic antidepressant effects when an organism is exposed to it at appropriate times during the circadian rhythm, regulating the sleep-wake cycle.

In addition to mood, learning and memory become impaired when the circadian system shifts due to light stimuli, which can be seen in studies modeling jet lag and shift work situations. Frontal and parietal lobe areas involved in working memory have been implicated in melanopsin responses to light information.

"In 2007, the International Agency for Research on Cancer classified shift work with circadian disruption or chronodisruption as a probable human carcinogen."

Exposure to light during the hours of melatonin production reduces melatonin production. Melatonin has been shown to mitigate the growth of tumors in rats. By suppressing the production of melatonin over the course of the night rats showed increased rates of tumors over the course of a four-week period.

Artificial light at night causing circadian disruption additionally impacts sex steroid production. Increased levels of progestogens and androgens was found in night shift workers as compared to "working hour" workers.

The proper exposure to light has become an accepted way to alleviate some of the effects of seasonal affective disorder (SAD). In addition exposure to light in the morning has been shown to assist Alzheimer patients in regulating their waking patterns.

In response to light exposure, alertness levels can increase as a result of suppression of melatonin secretion. A linear relationship has been found between alerting effects of light and activation in the posterior hypothalamus.

Disruption of circadian rhythm as a result of light also produces changes in metabolism.

Measured lighting for rating systems

Historically light was measured in the units of luminous intensity (candelas), luminance (candelas/m²) and illuminance (lumen/m²). After the discovery of ipRGCs in 2002 additional units of light measurement have been researched in order to better estimate the impact of different inputs of the spectrum of light on various photoreceptors. However, due to the variability in sensitivity between rods, cones and ipRGCs and variability between the different ipRGC types a singular unit does not perfectly reflect the effects of light on the human body.

The accepted current unit is equivalent melanopic lux which is a calculated ratio multiplied by the unit lux. The melanopic ratio is determined taking into account the source type of light and the melanopic illuminance values for the eye's photopigments. The source of light, the unit used to measure illuminance and the value of illuminance informs the spectral power distribution. This is used to calculate the Photopic illuminance and the melanopic lux for the five photopigments of the human eye, which is weighted based on the optical density of each photopigment.

The WELL Building standard was designed for "advancing health and well-being in buildings globally" Part of the standard is the implementation of Credit 54: Circadian Lighting Design. Specific thresholds for different office areas are designated in order to achieve credits. Light is measured at 1.2 meters above the finished floor for all areas.

Work areas must have at least a value of 200 equivalent melanopic lux present for 75% or more work stations between the hours of 9:00 A.M. and 1:00 P.M. for each day of the year when daylight is incorporated into calculations. If daylight is not taken into account all workstations require lighting at the value of 150 equivalent melanopic lux or greater.

Living environments, which are bedrooms, bathrooms and rooms with windows, at least one fixture must provide a melanopic lux value of at least 200 during the day and a melanopic lux value less than 50 during the night, measured .76 meters above the finished floor.

Breakrooms require an average melanopic lux of 250.

Learning areas require either that light models which may incorporate daylighting have an equivalent melanopic lux of 125 at at least 75% of desks for at least four hours per day or ambient lights maintain the standard lux recommendations set forth by Table 3 of the IES-ANSI RP-3-13.

The WELL Building standard additionally provides direction for circadian emulation in multi-family residences. In order to more accurately replicate natural cycles lighting users must be able to set a wake and bed time. An equivalent melanopic lux of 250 must be maintained in the period of the day between the indicated wake time and two hours before the indicated bed time. An equivalent melanopic lux of 50 or less is required for the period of the day spanning from two hours before the indicated bed time through the wake time. In addition at the indicated wake time melanopic lux should increase from 0 to 250 over the course of at least 15 minutes.

Other factors

Although many researchers consider light to be the strongest cue for entrainment, it is not the only factor acting on circadian rhythms. Other factors may enhance or decrease the effectiveness of entrainment. For instance, exercise and other physical activity, when coupled with light exposure, results in a somewhat stronger entrainment response. Other factors such as music and properly timed administration of the neurohormone melatonin have shown similar effects. Numerous other factors affect entrainment as well. These include feeding schedules, temperature, pharmacology, locomotor stimuli, social interaction, sexual stimuli and stress.

Circadian-based effects have also been found on visual perception to discomfort glare. The time of day is which people are shown a light source that produces visual discomfort is not perceived evenly. As the day progress, people tend to become more tolerant to the same levels of discomfort glare (i.e., people are more sensitive to discomfort glare in the morning compared to later in the day.) Further studies on chronotype show that early chronotypes can also tolerate more discomfort glare in the morning compared to late chronotypes.

Phytochrome

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Phytochrome

Phytochromes are a class of photoreceptor proteins found in plants, bacteria and fungi. They respond to light in the red and far-red regions of the visible spectrum and can be classed as either Type I, which are activated by far-red light, or Type II that are activated by red light. Recent advances have suggested that phytochromes also act as temperature sensors, as warmer temperatures enhance their de-activation. All of these factors contribute to the plant's ability to germinate.

Phytochromes control many aspects of plant development. They regulate the germination of seeds (photoblasty), the synthesis of chlorophyll, the elongation of seedlings, the size, shape and number and movement of leaves and the timing of flowering in adult plants. Phytochromes are widely expressed across many tissues and developmental stages.

Other plant photoreceptors include cryptochromes and phototropins, which respond to blue and ultraviolet-A light and UVR8, which is sensitive to ultraviolet-B light.

Structure

Phytochromes consist of a protein, covalently linked to a light-sensing bilin chromophore. The protein part comprises two identical chains (A and B). Each chain has a PAS domain, GAF domain and PHY domain. Domain arrangements in plant, bacterial and fungal phytochromes are comparable, insofar as the three N-terminal domains are always PAS, GAF and PHY domains. However C-terminal domains are more divergent. The PAS domain serves as a signal sensor and the GAF domain is responsible for binding to cGMP and also senses light signals. Together, these subunits form the phytochrome region, which regulates physiological changes in plants to changes in red and far red light conditions. In plants, red light changes phytochrome to its biologically active form, while far red light changes the protein to its biologically inactive form.

Isoforms and states

Two hypotheses, explaining the light - induced phytochrome conversions (P_R - red form, P_IR - far red form, B - protein). Left - H⁺ dissociation. Right - formation of the chlorophyll-like ring.

Phytochromes are characterized by a red/far-red photochromicity. Photochromic pigments change their "color" (spectral absorbance properties) upon light absorption. In the case of phytochrome the ground state is P_r, the _r indicating that it absorbs red light particularly strongly. The absorbance maximum is a sharp peak 650–670 nm, so concentrated phytochrome solutions look turquoise-blue to the human eye when viewed with white light. But once a red photon has been absorbed, the pigment undergoes a rapid conformational change to form the P_fr state. Here _fr indicates that now not red but far-red (also called "near infra-red"; 705–740 nm) is differentially absorbed. This shift in absorbance is apparent to the human eye as a slightly more greenish color. When P_fr absorbs far-red light it is converted back to P_r. Hence, red light makes P_fr, far-red light makes P_r. In plants at least P_fr is the physiologically active or "signalling" state.

Phytochromes' effect on phototropism

Phytochromes also have the ability to sense light, which causes the plant to grow towards it. This is called phototropism. Janoudi and his fellow coworkers wanted to see what type of phytochrome was responsible for causing phototropism to occur, and performed a series of experiments. They found that blue light causes the plant Arabidopsis thaliana to exhibit a phototropic response; this curvature is heightened with the addition of red light. They also found that five different phytochromes were present in the plant, while some mutants that did not function properly expressed a lack of phytochromes. Two of these mutant variants were very important for this study: phyA-101 and phyB-1. These are the mutants of phytochrome A and B respectively. The normally functional phytochrome A causes a sensitivity to far red light, and it causes a regulation in the expression of curvature toward the light, whereas phytochrome B is more sensitive to the red light.

The experiment consisted in the wild-type form of Arabidopsis, phyA-101(phytochrome A (phyA) null mutant), phyB-1 (phytochrome B deficient mutant). They were then exposed to white light as a control blue and red light at different fluences of light, the curvature was measured. It was determined that in order to achieve a phenotype of that of the wild-type phyA-101 must be exposed to four orders of higher magnitude or about 100umol m⁻² fluence. However, the fluence that causes phyB-1 to exhibit the same curvature as the wild-type is identical to that of the wild-type. The phytochrome that expressed more than normal amounts of phytochrome A it was found that as the fluence increased the curvature also increased up to 10umol-m⁻² the curvature was similar to the wild-type. The phytochrome expressing more than normal amounts of phytochrome B exhibited curvatures similar to that of the wild type at different fluences of red light up until the fluence of 100umol-m⁻² at fluences higher than this curvature was much higher than the wild-type.

Thus, the experiment resulted in the finding that another phytochrome than just phytochrome A acts in influencing the curvature since the mutant is not that far off from the wild-type, and phyA is not expressed at all. Thus leading to the conclusion that two phases must be responsible for phototropism. They determined that the response occurs at low fluences, and at high fluences. This is because for phyA-101 the threshold for curvature occurred at higher fluences, but curvature also occurs at low fluence values. Since the threshold of the mutant occurs at high fluence values it has been determined that phytochrome A is not responsible for curvature at high fluence values. Since the mutant for phytochrome B exhibited a response similar to that of the wild-type, it had been concluded that phytochrome B is not needed for low or high fluence exposure enhancement. It was predicted that the mutants that over expressed phytochrome A and B would be more sensitive. However, it is shown that an over expression of phy A does not really effect the curvature, thus there is enough of the phytochrome in the wild-type to achieve maximum curvature. For the phytochrome B over expression mutant higher curvature than normal at higher fluences of light indicated that phy B controls curvature at high fluences. Overall, they concluded that phytochrome A controls curvature at low fluences of light.

Phytochrome effect on root growth

Phytochromes can also affect root growth. It has been well documented that gravitropism is the main tropism in roots. However, a recent study has shown that phototropism also plays a role. A red light induced positive phototropism has been recently recorded in an experiment that used Arabidopsis to test where in the plant had the most effect on a positive phototropic response. The experimenters utilized an apparatus that allowed for root apex to be zero degrees so that gravitropism could not be a competing factor. When placed in red light, Arabidopsis roots displayed a curvature of 30 to 40 degrees. This showed a positive phototropic response in the red light. They then wanted to pinpoint exactly where in the plant light is received. When roots were covered there was little to no curvature of the roots when exposed to red light. In contrast, when shoots were covered, there was a positive phototropic response to the red light. This proves that lateral roots is where light sensing takes place. In order to further gather information regarding the phytochromes involved in this activity, phytochrome A, B, D and E mutants, and WT roots were exposed to red light. Phytochrome A and B mutants were severely impaired. There was no significant difference in the response of phyD and phyE compared with the wildtype, proving that phyA and phyB are responsible for positive phototropism in roots.   

Biochemistry

Chemically, phytochrome consists of a chromophore, a single bilin molecule consisting of an open chain of four pyrrole rings, covalently bonded to the protein moiety via highly conserved cysteine amino acid. It is the chromophore that absorbs light, and as a result changes the conformation of bilin and subsequently that of the attached protein, changing it from one state or isoform to the other.

The phytochrome chromophore is usually phytochromobilin, and is closely related to phycocyanobilin (the chromophore of the phycobiliproteins used by cyanobacteria and red algae to capture light for photosynthesis) and to the bile pigment bilirubin (whose structure is also affected by light exposure, a fact exploited in the phototherapy of jaundiced newborns). The term "bili" in all these names refers to bile. Bilins are derived from the closed tetrapyrrole ring of haem by an oxidative reaction catalyzed by haem oxygenase to yield their characteristic open chain. Chlorophyll and haem (Heme) share a common precursor in the form of Protoporphyrin IX, and share the same characteristic closed tetrapyrrole ring structure. In contrast to bilins, haem and chlorophyll carry a metal atom in the center of the ring, iron or magnesium, respectively.

The P_fr state passes on a signal to other biological systems in the cell, such as the mechanisms responsible for gene expression. Although this mechanism is almost certainly a biochemical process, it is still the subject of much debate. It is known that although phytochromes are synthesized in the cytosol and the P_r form is localized there, the P_fr form, when generated by light illumination, is translocated to the cell nucleus. This implies a role of phytochrome in controlling gene expression, and many genes are known to be regulated by phytochrome, but the exact mechanism has still to be fully discovered. It has been proposed that phytochrome, in the P_fr form, may act as a kinase, and it has been demonstrated that phytochrome in the P_fr form can interact directly with transcription factors.

Discovery

The phytochrome pigment was discovered by Sterling Hendricks and Harry Borthwick at the USDA-ARS Beltsville Agricultural Research Center in Maryland during a period from the late 1940s to the early 1960s. Using a spectrograph built from borrowed and war-surplus parts, they discovered that red light was very effective for promoting germination or triggering flowering responses. The red light responses were reversible by far-red light, indicating the presence of a photoreversible pigment.

The phytochrome pigment was identified using a spectrophotometer in 1959 by biophysicist Warren Butler and biochemist Harold Siegelman. Butler was also responsible for the name, phytochrome.

In 1983 the laboratories of Peter Quail and Clark Lagarias reported the chemical purification of the intact phytochrome molecule, and in 1985 the first phytochrome gene sequence was published by Howard Hershey and Peter Quail. By 1989, molecular genetics and work with monoclonal antibodies that more than one type of phytochrome existed; for example, the pea plant was shown to have at least two phytochrome types (then called type I (found predominantly in dark-grown seedlings) and type II (predominant in green plants)). It is now known by genome sequencing that Arabidopsis has five phytochrome genes (PHYA - E) but that rice has only three (PHYA - C). While this probably represents the condition in several di- and monocotyledonous plants, many plants are polyploid. Hence maize, for example, has six phytochromes - phyA1, phyA2, phyB1, phyB2, phyC1 and phyC2. While all these phytochromes have significantly different protein components, they all use phytochromobilin as their light-absorbing chromophore. Phytochrome A or phyA is rapidly degraded in the Pfr form - much more so than the other members of the family. In the late 1980s, the Vierstra lab showed that phyA is degraded by the ubiquitin system, the first natural target of the system to be identified in eukaryotes.

In 1996 David Kehoe and Arthur Grossman at the Carnegie Institution at Stanford University identified the proteins, in the filamentous cyanobacterium Fremyella diplosiphon called RcaE with similarly to plant phytochrome that controlled a red-green photoreversible response called chromatic acclimation and identified a gene in the sequenced, published genome of the cyanobacterium Synechocystis with closer similarity to those of plant phytochrome. This was the first evidence of phytochromes outside the plant kingdom. Jon Hughes in Berlin and Clark Lagarias at UC Davis subsequently showed that this Synechocystis gene indeed encoded a bona fide phytochrome (named Cph1) in the sense that it is a red/far-red reversible chromoprotein. Presumably plant phytochromes are derived from an ancestral cyanobacterial phytochrome, perhaps by gene migration from the chloroplast to the nucleus. Subsequently, phytochromes have been found in other prokaryotes including Deinococcus radiodurans and Agrobacterium tumefaciens. In Deinococcus phytochrome regulates the production of light-protective pigments, however in Synechocystis and Agrobacterium the biological function of these pigments is still unknown.

In 2005, the Vierstra and Forest labs at the University of Wisconsin published a three-dimensional structure of a truncated Deinococcus phytochrome (PAS/GAF domains). This paper revealed that the protein chain forms a knot - a highly unusual structure for a protein. In 2008, two groups around Essen and Hughes in Germany and Yang and Moffat in the US published the three-dimensional structures of the entire photosensory domain. One structures was for the Synechocystis sp. (strain PCC 6803) phytochrome in Pr and the other one for the Pseudomonas aeruginosa phytochrome in the P_fr state. The structures showed that a conserved part of the PHY domain, the so-called PHY tongue, adopts different folds. In 2014 it was confirmed by Takala et al that the refolding occurs even for the same phytochrome (from Deinococcus) as a function of illumination conditions.

Genetic engineering

Around 1989, several laboratories were successful in producing transgenic plants which produced elevated amounts of different phytochromes (overexpression). In all cases the resulting plants had conspicuously short stems and dark green leaves. Harry Smith and co-workers at Leicester University in England showed that by increasing the expression level of phytochrome A (which responds to far-red light), shade avoidance responses can be altered. As a result, plants can expend less energy on growing as tall as possible and have more resources for growing seeds and expanding their root systems. This could have many practical benefits: for example, grass blades that would grow more slowly than regular grass would not require mowing as frequently, or crop plants might transfer more energy to the grain instead of growing taller.

In 2002, the light-induced interaction between a plant phytochrome and phytochrome-interacting factor (PIF) was used to control gene transcription in yeast. This was the first example of using photoproteins from another organism for controlling a biochemical pathway.