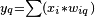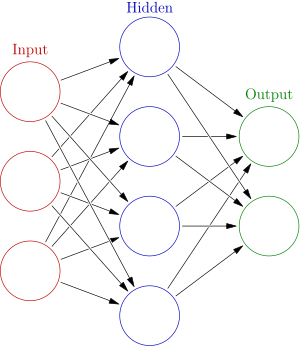
An artificial neural network is an interconnected group of nodes, akin to the vast network of
neurons in a
brain. Here, each circular node represents an artificial neuron and an arrow represents a connection from the output of one neuron to the input of another.
In
machine learning,
artificial neural networks (
ANNs) are a family of statistical learning algorithms inspired by
biological neural networks (the
central nervous systems of animals, in particular the
brain) and are used to estimate or
approximate functions that can depend on a large number of
inputs and are generally unknown. Artificial neural networks are generally presented as systems of interconnected "
neurons" which can compute values from inputs, and are capable of
machine learning as well as
pattern recognition thanks to their adaptive nature.
For example, a neural network for
handwriting recognition is defined by a set of input neurons which may be activated by the pixels of an input image. After being weighted and transformed by a
function (determined by the network's designer), the activations of these neurons are then passed on to other neurons. This process is repeated until finally, an output neuron is activated. This determines which character was read.
Like other machine learning methods - systems that learn from data - neural networks have been used to solve a wide variety of tasks that are hard to solve using ordinary
rule-based programming, including
computer vision and
speech recognition.
Background
Examinations of the human's
central nervous system inspired the concept of neural networks. In an Artificial Neural Network, simple artificial
nodes, known as "
neurons", "neurodes", "processing elements" or "units", are connected together to form a network which mimics a biological neural network.
There is no single formal definition of what an artificial neural network is. However, a class of statistical models may commonly be called "Neural" if they possess the following characteristics:
- consist of sets of adaptive weights, i.e. numerical parameters that are tuned by a learning algorithm, and
- are capable of approximating non-linear functions of their inputs.
The adaptive weights are conceptually connection strengths between neurons, which are activated during training and prediction.
Neural networks are similar to biological neural networks in performing functions collectively and in parallel by the units, rather than there being a clear delineation of subtasks to which various units are assigned. The term "neural network" usually refers to models employed in
statistics,
cognitive psychology and
artificial intelligence. Neural network models which emulate the central nervous system are part of
theoretical neuroscience and
computational neuroscience.
In modern
software implementations of artificial neural networks, the approach inspired by biology has been largely abandoned for a more practical approach based on statistics and signal processing. In some of these systems, neural networks or parts of neural networks (like artificial neurons) form components in larger systems that combine both adaptive and non-adaptive elements. While the more general approach of such systems is more suitable for real-world problem solving, it has little to do with the traditional artificial intelligence connectionist models. What they do have in common, however, is the principle of non-linear, distributed, parallel and local processing and adaptation. Historically, the use of neural networks models marked a paradigm shift in the late eighties from high-level (symbolic)
artificial intelligence, characterized by
expert systems with knowledge embodied in
if-then rules, to low-level (sub-symbolic)
machine learning, characterized by knowledge embodied in the parameters of a
dynamical system.
History
Warren McCulloch and
Walter Pitts[1] (1943) created a computational model for neural networks based on
mathematics and algorithms. They called this model
threshold logic. The model paved the way for neural network research to split into two distinct approaches. One approach focused on biological processes in the brain and the other focused on the application of neural networks to artificial intelligence.
In the late 1940s psychologist
Donald Hebb[2] created a hypothesis of learning based on the mechanism of neural plasticity that is now known as
Hebbian learning. Hebbian learning is considered to be a 'typical'
unsupervised learning rule and its later variants were early models for
long term potentiation. These ideas started being applied to computational models in 1948 with
Turing's B-type machines.
Farley and
Wesley A. Clark[3] (1954) first used computational machines, then called calculators, to simulate a Hebbian network at MIT. Other neural network computational machines were created by Rochester, Holland, Habit, and Duda
[4] (1956).
Frank Rosenblatt[5] (1958) created the
perceptron, an algorithm for pattern recognition based on a two-layer learning computer network using simple addition and subtraction. With mathematical notation, Rosenblatt also described circuitry not in the basic perceptron, such as the
exclusive-or circuit, a circuit whose mathematical computation could not be processed until after the
backpropagation algorithm was created by
Paul Werbos[6] (1975).
Neural network research stagnated after the publication of machine learning research by
Marvin Minsky and
Seymour Papert[7] (1969). They discovered two key issues with the computational machines that processed neural networks. The first issue was that single-layer neural networks were incapable of processing the exclusive-or circuit. The second significant issue was that computers were not sophisticated enough to effectively handle the long run time required by large neural networks. Neural network research slowed until computers achieved greater processing power. Also key later advances was the
backpropagation algorithm which effectively solved the exclusive-or problem (Werbos 1975).
[6]
The
parallel distributed processing of the mid-1980s became popular under the name
connectionism. The text by
David E. Rumelhart and
James McClelland[8] (1986) provided a full exposition on the use of connectionism in computers to simulate neural processes.
Neural networks, as used in artificial intelligence, have traditionally been viewed as simplified models of
neural processing in the brain, even though the relation between this model and brain biological architecture is debated, as it is not clear to what degree artificial neural networks mirror brain function.
[9]
In the 1990s, neural networks were overtaken in popularity in machine learning by
support vector machines and other, much simpler methods such as
linear classifiers. Renewed interest in neural nets was sparked in the 2000s by the advent of
deep learning.
Recent improvements
Computational devices have been created in
CMOS, for both biophysical simulation and
neuromorphic computing. More recent efforts show promise for creating
nanodevices[10] for very large scale
principal components analyses and
convolution. If successful, these efforts could usher in a new era of
neural computing[11] that is a step beyond digital computing, because it depends on
learning rather than
programming and because it is fundamentally
analog rather than
digital even though the first instantiations may in fact be with CMOS digital devices.
Between 2009 and 2012, the
recurrent neural networks and deep feedforward neural networks developed in the research group of
Jürgen Schmidhuber at the
Swiss AI Lab IDSIA have won eight international competitions in
pattern recognition and
machine learning.
[12] For example, multi-dimensional
long short term memory (LSTM)
[13][14] won three competitions in connected handwriting recognition at the 2009 International Conference on Document Analysis and Recognition (ICDAR), without any prior knowledge about the three different languages to be learned.
Variants of the
back-propagation algorithm as well as unsupervised methods by
Geoff Hinton and colleagues at the
University of Toronto[15][16] can be used to train deep, highly nonlinear neural architectures similar to the 1980
Neocognitron by
Kunihiko Fukushima,
[17] and the "standard architecture of vision",
[18] inspired by the simple and complex cells identified by
David H. Hubel and
Torsten Wiesel in the primary
visual cortex.
Deep learning feedforward networks, such as
convolutional neural networks, alternate
convolutional layers and max-pooling layers, topped by several pure
classification layers. Fast
GPU-based implementations of this approach have won several pattern recognition contests, including the IJCNN 2011 Traffic Sign Recognition Competition
[19] and the ISBI 2012 Segmentation of Neuronal Structures in Electron Microscopy Stacks challenge.
[20] Such neural networks also were the first artificial pattern recognizers to achieve human-competitive or even superhuman performance
[21] on benchmarks such as traffic sign recognition (IJCNN 2012), or the
MNIST handwritten digits problem of
Yann LeCun and colleagues at
NYU.
Successes in pattern recognition contests since 2009
Between 2009 and 2012, the
recurrent neural networks and deep feedforward neural networks developed in the research group of
Jürgen Schmidhuber at the
Swiss AI Lab IDSIA have won eight international competitions in
pattern recognition and
machine learning.
[22] For example, the bi-directional and
multi-dimensional long short term memory (LSTM)
[23][24] of Alex Graves et al. won three competitions in connected handwriting recognition at the 2009 International Conference on Document Analysis and Recognition (ICDAR), without any prior knowledge about the three different languages to be learned. Fast
GPU-based implementations of this approach by Dan Ciresan and colleagues at
IDSIA have won several pattern recognition contests, including the IJCNN 2011 Traffic Sign Recognition Competition,
[25] the ISBI 2012 Segmentation of Neuronal Structures in Electron Microscopy Stacks challenge,
[20] and others. Their neural networks also were the first artificial pattern recognizers to achieve human-competitive or even superhuman performance
[21] on important benchmarks such as traffic sign recognition (IJCNN 2012), or the
MNIST handwritten digits problem of
Yann LeCun at
NYU. Deep, highly nonlinear neural architectures similar to the 1980
neocognitron by
Kunihiko Fukushima[17] and the "standard architecture of vision"
[18] can also be pre-trained by unsupervised methods
[26][27] of
Geoff Hinton's lab at
University of Toronto. A team from this lab won a 2012 contest sponsored by
Merck to design software to help find molecules that might lead to new drugs.
[28]
Models
Neural network models in artificial intelligence are usually referred to as artificial neural networks (ANNs); these are essentially simple mathematical models defining a function
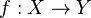
or a distribution over

or both

and
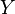
, but sometimes models are also intimately associated with a particular learning algorithm or learning rule. A common use of the phrase ANN model really means the definition of a
class of such functions (where members of the class are obtained by varying parameters, connection weights, or specifics of the architecture such as the number of neurons or their connectivity).
Network function
The word
network in the term 'artificial neural network' refers to the inter–connections between the neurons in the different layers of each system. An example system has three layers. The first layer has input neurons which send data via synapses to the second layer of neurons, and then via more synapses to the third layer of output neurons. More complex systems will have more layers of neurons with some having increased layers of input neurons and output neurons. The synapses store parameters called "weights" that manipulate the data in the calculations.
An ANN is typically defined by three types of parameters:
- The interconnection pattern between the different layers of neurons
- The learning process for updating the weights of the interconnections
- The activation function that converts a neuron's weighted input to its output activation.
Mathematically, a neuron's network function
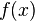
is defined as a composition of other functions
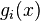
, which can further be defined as a composition of other functions. This can be conveniently represented as a network structure, with arrows depicting the dependencies between variables. A widely used type of composition is the
nonlinear weighted sum, where

, where

(commonly referred to as the
activation function[29]) is some predefined function, such as the
hyperbolic tangent. It will be convenient for the following to refer to a collection of functions

as simply a vector

.
This figure depicts such a decomposition of

, with dependencies between variables indicated by arrows. These can be interpreted in two ways.
The first view is the functional view: the input

is transformed into a 3-dimensional vector

, which is then transformed into a 2-dimensional vector

, which is finally transformed into

. This view is most commonly encountered in the context of
optimization.
The second view is the probabilistic view: the
random variable 
depends upon the random variable

, which depends upon

, which depends upon the random variable

. This view is most commonly encountered in the context of
graphical models.
The two views are largely equivalent. In either case, for this particular network architecture, the components of individual layers are independent of each other (e.g., the components of

are independent of each other given their input

). This naturally enables a degree of parallelism in the implementation.

Two separate depictions of the recurrent ANN dependency graph
Networks such as the previous one are commonly called
feedforward, because their graph is a
directed acyclic graph. Networks with
cycles are commonly called
recurrent. Such networks are commonly depicted in the manner shown at the top of the figure, where

is shown as being dependent upon itself. However, an implied temporal dependence is not shown.
Learning
What has attracted the most interest in neural networks is the possibility of
learning. Given a specific
task to solve, and a
class of functions

, learning means using a set of
observations to find
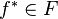
which solves the task in some
optimal sense.
This entails defining a cost function

such that, for the optimal solution

,

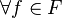
– i.e., no solution has a cost less than the cost of the optimal solution.
The cost function
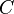
is an important concept in learning, as it is a measure of how far away a particular solution is from an optimal solution to the problem to be solved. Learning algorithms search through the solution space to find a function that has the smallest possible cost.
For applications where the solution is dependent on some data, the cost must necessarily be a
function of the observations, otherwise we would not be modelling anything related to the data. It is frequently defined as a
statistic to which only approximations can be made. As a simple example, consider the problem of finding the model

, which minimizes
![\textstyle C=E\left[(f(x) - y)^2\right]](//upload.wikimedia.org/math/4/a/3/4a31869daf321286e1c55e3f8fc239cc.png)
, for data pairs

drawn from some distribution

. In practical situations we would only have
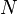
samples from

and thus, for the above example, we would only minimize

. Thus, the cost is minimized over a sample of the data rather than the entire data set.
When

some form of
online machine learning must be used, where the cost is partially minimized as each new example is seen. While online machine learning is often used when

is fixed, it is most useful in the case where the distribution changes slowly over time. In neural network methods, some form of online machine learning is frequently used for finite datasets.
Choosing a cost function
While it is possible to define some arbitrary
ad hoc cost function, frequently a particular cost will be used, either because it has desirable properties (such as
convexity) or because it arises naturally from a particular formulation of the problem (e.g., in a probabilistic formulation the posterior probability of the model can be used as an inverse cost). Ultimately, the cost function will depend on the desired task. An overview of the three main categories of learning tasks is provided below:
Learning paradigms
There are three major learning paradigms, each corresponding to a particular abstract learning task. These are
supervised learning,
unsupervised learning and
reinforcement learning.
Supervised learning
In
supervised learning, we are given a set of example pairs

and the aim is to find a function
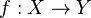
in the allowed class of functions that matches the examples. In other words, we wish to
infer the mapping implied by the data; the cost function is related to the mismatch between our mapping and the data and it implicitly contains prior knowledge about the problem domain.
A commonly used cost is the
mean-squared error, which tries to minimize the average squared error between the network's output, f(x), and the target value y over all the example pairs. When one tries to minimize this cost using
gradient descent for the class of neural networks called
multilayer perceptrons, one obtains the common and well-known
backpropagation algorithm for training neural networks.
Tasks that fall within the paradigm of supervised learning are
pattern recognition (also known as classification) and
regression (also known as function approximation). The supervised learning paradigm is also applicable to sequential data (e.g., for speech and gesture recognition). This can be thought of as learning with a "teacher," in the form of a function that provides continuous feedback on the quality of solutions obtained thus far.
Unsupervised learning
In
unsupervised learning, some data

is given and the cost function to be minimized, that can be any function of the data

and the network's output,

.
The cost function is dependent on the task (what we are trying to model) and our
a priori assumptions (the implicit properties of our model, its parameters and the observed variables).
As a trivial example, consider the model

where

is a constant and the cost
![\textstyle C=E[(x - f(x))^2]](//upload.wikimedia.org/math/2/2/6/226068c9e757f12750363490dfdc6a42.png)
. Minimizing this cost will give us a value of

that is equal to the mean of the data. The cost function can be much more complicated. Its form depends on the application: for example, in compression it could be related to the
mutual information between

and
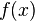
, whereas in statistical modeling, it could be related to the
posterior probability of the model given the data. (Note that in both of those examples those quantities would be maximized rather than minimized).
Tasks that fall within the paradigm of unsupervised learning are in general
estimation problems; the applications include
clustering, the estimation of
statistical distributions,
compression and
filtering.
Reinforcement learning
In
reinforcement learning, data

are usually not given, but generated by an agent's interactions with the environment. At each point in time
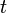
, the agent performs an action
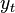
and the environment generates an observation

and an instantaneous cost
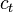
, according to some (usually unknown) dynamics. The aim is to discover a
policy for selecting actions that minimizes some measure of a long-term cost; i.e., the expected cumulative cost. The environment's dynamics and the long-term cost for each policy are usually unknown, but can be estimated.
More formally the environment is modelled as a
Markov decision process (MDP) with states

and actions

with the following probability distributions: the instantaneous cost distribution

, the observation distribution

and the transition

, while a policy is defined as conditional distribution over actions given the observations. Taken together, the two then define a
Markov chain (MC). The aim is to discover the policy that minimizes the cost; i.e., the MC for which the cost is minimal.
ANNs are frequently used in reinforcement learning as part of the overall algorithm.
[30][31] Dynamic programming has been coupled with ANNs (Neuro dynamic programming) by
Bertsekas and Tsitsiklis
[32] and applied to multi-dimensional nonlinear problems such as those involved in
vehicle routing,
[33] natural resources management[34][35] or
medicine[36] because of the ability of ANNs to mitigate losses of accuracy even when reducing the discretization grid density for numerically approximating the solution of the original control problems.
Tasks that fall within the paradigm of reinforcement learning are control problems,
games and other
sequential decision making tasks.
Learning algorithms
Training a neural network model essentially means selecting one model from the set of allowed models (or, in a
Bayesian framework, determining a distribution over the set of allowed models) that minimizes the cost criterion. There are numerous algorithms available for training neural network models; most of them can be viewed as a straightforward application of
optimization theory and
statistical estimation.
Most of the algorithms used in training artificial neural networks employ some form of
gradient descent, using backpropagation to compute the actual gradients. This is done by simply taking the derivative of the cost function with respect to the network parameters and then changing those parameters in a
gradient-related direction.
Evolutionary methods,
[37] gene expression programming,
[38] simulated annealing,
[39] expectation-maximization,
non-parametric methods and
particle swarm optimization[40] are some commonly used methods for training neural networks.
Employing artificial neural networks
Perhaps the greatest advantage of ANNs is their ability to be used as an arbitrary function approximation mechanism that 'learns' from observed data. However, using them is not so straightforward, and a relatively good understanding of the underlying theory is essential.
- Choice of model: This will depend on the data representation and the application. Overly complex models tend to lead to problems with learning.
- Learning algorithm: There are numerous trade-offs between learning algorithms. Almost any algorithm will work well with the correct hyperparameters for training on a particular fixed data set. However, selecting and tuning an algorithm for training on unseen data requires a significant amount of experimentation.
- Robustness: If the model, cost function and learning algorithm are selected appropriately the resulting ANN can be extremely robust.
With the correct implementation, ANNs can be used naturally in
online learning and large data set applications. Their simple implementation and the existence of mostly local dependencies exhibited in the structure allows for fast, parallel implementations in hardware.
Applications
The utility of artificial neural network models lies in the fact that they can be used to infer a function from observations. This is particularly useful in applications where the complexity of the data or task makes the design of such a function by hand impractical.
Real-life applications
The tasks artificial neural networks are applied to tend to fall within the following broad categories:
- Function approximation, or regression analysis, including time series prediction, fitness approximation and modeling.
- Classification, including pattern and sequence recognition, novelty detection and sequential decision making.
- Data processing, including filtering, clustering, blind source separation and compression.
- Robotics, including directing manipulators, prosthesis.
- Control, including Computer numerical control.
Application areas include the system identification and control (vehicle control, process control,
natural resources management), quantum chemistry,
[41] game-playing and decision making (backgammon, chess,
poker), pattern recognition (radar systems, face identification, object recognition and more), sequence recognition (gesture, speech, handwritten text recognition), medical diagnosis, financial applications (e.g.
automated trading systems),
data mining (or knowledge discovery in databases, "KDD"), visualization and
e-mail spam filtering.
Artificial neural networks have also been used to diagnose several cancers. An ANN based hybrid lung cancer detection system named HLND improves the accuracy of diagnosis and the speed of lung cancer radiology.
[42] These networks have also been used to diagnose prostate cancer. The diagnoses can be used to make specific models taken from a large group of patients compared to information of one given patient. The models do not depend on assumptions about correlations of different variables. Colorectal cancer has also been predicted using the neural networks. Neural networks could predict the outcome for a patient with colorectal cancer with more accuracy than the current clinical methods. After training, the networks could predict multiple patient outcomes from unrelated institutions.
[43]
Neural networks and neuroscience
Theoretical and
computational neuroscience is the field concerned with the theoretical analysis and the computational modeling of biological neural systems. Since neural systems are intimately related to cognitive processes and behavior, the field is closely related to cognitive and behavioral modeling.
The aim of the field is to create models of biological neural systems in order to understand how biological systems work. To gain this understanding, neuroscientists strive to make a link between observed biological processes (data), biologically plausible mechanisms for neural processing and learning (
biological neural network models) and theory (statistical learning theory and
information theory).
Types of models
Many models are used in the field, defined at different levels of abstraction and modeling different aspects of neural systems. They range from models of the short-term behavior of
individual neurons, models of how the dynamics of neural circuitry arise from interactions between individual neurons and finally to models of how behavior can arise from abstract neural modules that represent complete subsystems. These include models of the long-term, and short-term plasticity, of neural systems and their relations to learning and memory from the individual neuron to the system level.
Neural network software
Neural network software is used to
simulate,
research, develop and apply artificial neural networks,
biological neural networks and, in some cases, a wider array of
adaptive systems.
Types of artificial neural networks
Artificial neural network types vary from those with only one or two layers of single direction logic, to complicated multi–input many directional feedback loops and layers. On the whole, these systems use algorithms in their programming to determine control and organization of their functions. Most systems use "weights" to change the parameters of the throughput and the varying connections to the neurons. Artificial neural networks can be autonomous and learn by input from outside "teachers" or even self-teaching from written-in rules.
Theoretical properties
Computational power
The
multi-layer perceptron (MLP) is a universal function approximator, as proven by the
universal approximation theorem. However, the proof is not constructive regarding the number of neurons required or the settings of the weights.
Work by
Hava Siegelmann and
Eduardo D. Sontag has provided a proof that a specific recurrent architecture with rational valued weights (as opposed to full precision
real number-valued weights) has the full power of a
Universal Turing Machine[44] using a finite number of neurons and standard linear connections. They have further shown that the use of irrational values for weights results in a machine with
super-Turing power.
[45]
Capacity
Artificial neural network models have a property called 'capacity', which roughly corresponds to their ability to model any given function. It is related to the amount of information that can be stored in the network and to the notion of complexity.
Convergence
Nothing can be said in general about convergence since it depends on a number of factors. Firstly, there may exist many local minima. This depends on the cost function and the model. Secondly, the optimization method used might not be guaranteed to converge when far away from a local minimum. Thirdly, for a very large amount of data or parameters, some methods become impractical.
In general, it has been found that theoretical guarantees regarding convergence are an unreliable guide to practical application.
[citation needed]
Generalization and statistics
In applications where the goal is to create a system that generalizes well in unseen examples, the problem of over-training has emerged. This arises in convoluted or over-specified systems when the capacity of the network significantly exceeds the needed free parameters. There are two schools of thought for avoiding this problem: The first is to use
cross-validation and similar techniques to check for the presence of overtraining and optimally select hyperparameters such as to minimize the generalization error. The second is to use some form of
regularization. This is a concept that emerges naturally in a probabilistic (Bayesian) framework, where the regularization can be performed by selecting a larger prior probability over simpler models; but also in statistical learning theory, where the goal is to minimize over two quantities: the 'empirical risk' and the 'structural risk', which roughly corresponds to the error over the training set and the predicted error in unseen data due to overfitting.

Confidence analysis of a neural network
Supervised neural networks that use an
MSE cost function can use formal statistical methods to determine the confidence of the trained model. The MSE on a validation set can be used as an estimate for variance. This value can then be used to calculate the
confidence interval of the output of the network, assuming a
normal distribution. A confidence analysis made this way is statistically valid as long as the output
probability distribution stays the same and the network is not modified.
By assigning a
softmax activation function, a generalization of the
logistic function, on the output layer of the neural network (or a softmax component in a component-based neural network) for categorical target variables, the outputs can be interpreted as posterior probabilities. This is very useful in classification as it gives a certainty measure on classifications.
The softmax activation function is:

Controversies
Training issues
A common criticism of neural networks, particularly in robotics, is that they require a large diversity of training for real-world operation
[citation needed]. This is not surprising, since any learning machine needs sufficient representative examples in order to capture the underlying structure that allows it to generalize to new cases. Dean Pomerleau, in his research presented in the paper "Knowledge-based Training of Artificial Neural Networks for Autonomous Robot Driving," uses a neural network to train a robotic vehicle to drive on multiple types of roads (single lane, multi-lane, dirt, etc.). A large amount of his research is devoted to (1) extrapolating multiple training scenarios from a single training experience, and (2) preserving past training diversity so that the system does not become overtrained (if, for example, it is presented with a series of right turns – it should not learn to always turn right). These issues are common in neural networks that must decide from amongst a wide variety of responses, but can be dealt with in several ways, for example by randomly shuffling the training examples, by using a numerical optimization algorithm that does not take too large steps when changing the network connections following an example, or by grouping examples in so-called mini-batches.
A. K. Dewdney, a former
Scientific American columnist, wrote in 1997, "Although neural nets do solve a few toy problems, their powers of computation are so limited that I am surprised anyone takes them seriously as a general problem-solving tool." (Dewdney, p. 82)
Hardware issues
To implement large and effective software neural networks, considerable processing and storage resources need to be committed
[citation needed]. While the brain has hardware tailored to the task of processing signals through a
graph of neurons, simulating even a most simplified form on
Von Neumann technology may compel a neural network designer to fill many millions of
database rows for its connections – which can consume vast amounts of computer
memory and
hard disk space.
Furthermore, the designer of neural network systems will often need to simulate the transmission of signals through many of these connections and their associated neurons – which must often be matched with incredible amounts of
CPU processing power and time. While neural networks often yield
effective programs, they too often do so at the cost of
efficiency (they tend to consume considerable amounts of time and money).
Computing power continues to grow roughly according to
Moore's Law, which may provide sufficient resources to accomplish new tasks.
Neuromorphic engineering addresses the hardware difficulty directly, by constructing non-Von-Neumann chips with circuits designed to implement neural nets from the ground up.
Practical counterexamples to criticisms
Arguments against Dewdney's position are that neural networks have been successfully used to solve many complex and diverse tasks, ranging from autonomously flying aircraft
[46] to detecting credit card fraud .
[citation needed]
Technology writer
Roger Bridgman commented on Dewdney's statements about neural nets:
Neural networks, for instance, are in the dock not only because they have been hyped to high heaven, (what hasn't?) but also because you could create a successful net without understanding how it worked: the bunch of numbers that captures its behaviour would in all probability be "an opaque, unreadable table...valueless as a scientific resource".
In spite of his emphatic declaration that science is not technology, Dewdney seems here to pillory neural nets as bad science when most of those devising them are just trying to be good engineers. An unreadable table that a useful machine could read would still be well worth having.[47]
Although it is true that analyzing what has been learned by an artificial neural network is difficult, it is much easier to do so than to analyze what has been learned by a biological neural network.
Furthermore, researchers involved in exploring learning algorithms for neural networks are gradually uncovering generic principles which allow a learning machine to be successful. For example, Bengio and LeCun (2007) wrote an article regarding local vs non-local learning, as well as shallow vs deep architecture.
[48]
Hybrid approaches
Some other criticisms came from believers of hybrid models (combining neural networks and symbolic approaches). They advocate the intermix of these two approaches and believe that hybrid models can better capture the mechanisms of the human mind.
[49][50]
Gallery
-
A single-layer feedforward artificial neural network. Arrows originating from

are omitted for clarity. There are p inputs to this network and q outputs. In this system, the value of the qth output,

would be calculated as
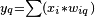
-
A two-layer feedforward artificial neural network.
-
-


 or a distribution over
or a distribution over  or both
or both  , but sometimes models are also intimately associated with a particular learning algorithm or learning rule. A common use of the phrase ANN model really means the definition of a class of such functions (where members of the class are obtained by varying parameters, connection weights, or specifics of the architecture such as the number of neurons or their connectivity).
, but sometimes models are also intimately associated with a particular learning algorithm or learning rule. A common use of the phrase ANN model really means the definition of a class of such functions (where members of the class are obtained by varying parameters, connection weights, or specifics of the architecture such as the number of neurons or their connectivity).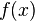 is defined as a composition of other functions
is defined as a composition of other functions 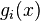 , which can further be defined as a composition of other functions. This can be conveniently represented as a network structure, with arrows depicting the dependencies between variables. A widely used type of composition is the nonlinear weighted sum, where
, which can further be defined as a composition of other functions. This can be conveniently represented as a network structure, with arrows depicting the dependencies between variables. A widely used type of composition is the nonlinear weighted sum, where  , where
, where  (commonly referred to as the
(commonly referred to as the  as simply a vector
as simply a vector  .
.
 , with dependencies between variables indicated by arrows. These can be interpreted in two ways.
, with dependencies between variables indicated by arrows. These can be interpreted in two ways. is transformed into a 3-dimensional vector
is transformed into a 3-dimensional vector  , which is then transformed into a 2-dimensional vector
, which is then transformed into a 2-dimensional vector  , which is finally transformed into
, which is finally transformed into  depends upon the random variable
depends upon the random variable  , which depends upon
, which depends upon  , which depends upon the random variable
, which depends upon the random variable 
 , learning means using a set of observations to find
, learning means using a set of observations to find 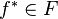 which solves the task in some optimal sense.
which solves the task in some optimal sense. such that, for the optimal solution
such that, for the optimal solution  ,
, 
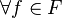 – i.e., no solution has a cost less than the cost of the optimal solution.
– i.e., no solution has a cost less than the cost of the optimal solution.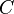 is an important concept in learning, as it is a measure of how far away a particular solution is from an optimal solution to the problem to be solved. Learning algorithms search through the solution space to find a function that has the smallest possible cost.
is an important concept in learning, as it is a measure of how far away a particular solution is from an optimal solution to the problem to be solved. Learning algorithms search through the solution space to find a function that has the smallest possible cost.![\textstyle C=E\left[(f(x) - y)^2\right]](http://upload.wikimedia.org/math/4/a/3/4a31869daf321286e1c55e3f8fc239cc.png) , for data pairs
, for data pairs  drawn from some distribution
drawn from some distribution  . In practical situations we would only have
. In practical situations we would only have 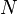 samples from
samples from  . Thus, the cost is minimized over a sample of the data rather than the entire data set.
. Thus, the cost is minimized over a sample of the data rather than the entire data set. some form of
some form of  and the aim is to find a function
and the aim is to find a function  where
where  is a constant and the cost
is a constant and the cost ![\textstyle C=E[(x - f(x))^2]](http://upload.wikimedia.org/math/2/2/6/226068c9e757f12750363490dfdc6a42.png) . Minimizing this cost will give us a value of
. Minimizing this cost will give us a value of 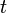 , the agent performs an action
, the agent performs an action 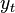 and the environment generates an observation
and the environment generates an observation  and an instantaneous cost
and an instantaneous cost 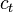 , according to some (usually unknown) dynamics. The aim is to discover a policy for selecting actions that minimizes some measure of a long-term cost; i.e., the expected cumulative cost. The environment's dynamics and the long-term cost for each policy are usually unknown, but can be estimated.
, according to some (usually unknown) dynamics. The aim is to discover a policy for selecting actions that minimizes some measure of a long-term cost; i.e., the expected cumulative cost. The environment's dynamics and the long-term cost for each policy are usually unknown, but can be estimated. and actions
and actions  with the following probability distributions: the instantaneous cost distribution
with the following probability distributions: the instantaneous cost distribution  , the observation distribution
, the observation distribution  and the transition
and the transition  , while a policy is defined as conditional distribution over actions given the observations. Taken together, the two then define a
, while a policy is defined as conditional distribution over actions given the observations. Taken together, the two then define a 


 are omitted for clarity. There are p inputs to this network and q outputs. In this system, the value of the qth output,
are omitted for clarity. There are p inputs to this network and q outputs. In this system, the value of the qth output,  would be calculated as
would be calculated as