From Wikipedia, the free encyclopedia
In thermodynamics, the Gibbs free energy (IUPAC recommended name: Gibbs energy or Gibbs function; also known as free enthalpy[1] to distinguish it from Helmholtz free energy) is a thermodynamic potential that measures the "usefulness" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure (isothermal, isobaric). Just as in mechanics, where potential energy is defined as capacity to do work, similarly different potentials have different meanings. The Gibbs free energy (SI units kJ/mol) is the maximum amount of non-expansion work that can be extracted from a thermodynamically closed system (one that can exchange heat and work with its surroundings, but not matter); this maximum can be attained only in a completely reversible process. When a system changes from a well-defined initial state to a well-defined final state, the Gibbs free energy change ΔP equals the work exchanged by the system with its surroundings, minus the work of the pressure forces, during a reversible transformation of the system from the initial state to the final state.[2]
Gibbs energy (also referred to as ∆P) is also the chemical potential that is minimized when a system reaches equilibrium at constant pressure and temperature. Its derivative with respect to the reaction coordinate of the system vanishes at the equilibrium point. As such, it is a convenient criterion for the spontaneity of processes with constant pressure and temperature.
The Gibbs free energy, originally called available energy, was developed in the 1870s by the American mathematician Josiah Willard Gibbs. In 1873, Gibbs described this "available energy" as
For systems reacting at STP (or any other fixed temperature and pressure), there is a general natural tendency to achieve a minimum of the free energy.
A quantitative measure of the favorability of a given reaction is the difference ΔG in Gibbs free energy that is (or would be) effected by proceeding with the reaction. When the calculated energetics of the process indicate that ΔG is negative, it means that the reaction will be favoured and will release energy. The energy released equals the maximum amount of work that can be performed as a result of the chemical reaction. In contrast, if conditions indicated a positive ΔG, then energy—in the form of work—would have to be added to the reacting system for the reaction to occur.
The equation can be also seen from the perspective of the system taken together with its surroundings (the rest of the universe). First assume that the given reaction is the only one that is occurring. Then the entropy released or absorbed by the system equals the entropy that the environment must absorb or release, respectively. The reaction will only be allowed if the total entropy change of the universe is zero or positive. This is reflected in a negative ΔG, and the reaction is called exergonic.
If we allow other reactions to occur on the side, then an otherwise endergonic chemical reaction (one with positive ΔG) can be made to happen. The input of heat into an inherently endergonic reaction, such as the elimination of cyclohexanol to cyclohexene, can be seen as coupling an unfavourable reaction (elimination) to a favourable one (burning of coal or other provision of heat) such that the total entropy change of the universe is greater than or equal to zero, making the total Gibbs free energy difference of the coupled reactions negative.
In traditional use, the term "free" was included in "Gibbs free energy" to mean "available in the form of useful work."[2] The characterization becomes more precise if we add the qualification that it is the energy available for non-volume work.[4] (A analogous, but slightly different, meaning of "free" applies in conjunction with the Helmholtz free energy, for systems at constant temperature). However, an increasing number of books and journal articles do not include the attachment "free", referring to G as simply "Gibbs energy". This is the result of a 1988 IUPAC meeting to set unified terminologies for the international scientific community, in which the adjective ‘free’ was supposedly banished.[5][6][7] This standard, however, has not yet been universally adopted.
In 1873, Willard Gibbs published A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces, in which he sketched the principles of his new equation that was able to predict or estimate the tendencies of various natural processes to ensue when bodies or systems are brought into contact. By studying the interactions of homogeneous substances in contact, i.e., bodies composed of part solid, part liquid, and part vapor, and by using a three-dimensional volume-entropy-internal energy graph, Gibbs was able to determine three states of equilibrium, i.e., "necessarily stable", "neutral", and "unstable", and whether or not changes would ensue.
Thereafter, in 1882, the German scientist Hermann von Helmholtz characterized the affinity as the largest quantity of work which can be gained when the reaction is carried out in a reversible manner, e.g., electrical work in a reversible cell. The maximum work is thus regarded as the diminution of the free, or available, energy of the system (Gibbs free energy G at T = constant, P = constant or Helmholtz free energy F at T = constant, V = constant), whilst the heat given out is usually a measure of the diminution of the total energy of the system (internal energy). Thus, G or F is the amount of energy "free" for work under the given conditions.
Until this point, the general view had been such that: "all chemical reactions drive the system to a state of equilibrium in which the affinities of the reactions vanish". Over the next 60 years, the term affinity came to be replaced with the term free energy. According to chemistry historian Henry Leicester, the influential 1923 textbook Thermodynamics and the Free Energy of Chemical Substances by Gilbert N. Lewis and Merle Randall led to the replacement of the term "affinity" by the term "free energy" in much of the English-speaking world.

The Gibbs free energy is defined as:
Any number of extra terms may be added, depending on the particular system being considered. Aside from mechanical work, a system may, in addition, perform numerous other types of work. For example, in the infinitesimal expression, the contractile work energy associated with a thermodynamic system that is a contractile fiber that shortens by an amount −dl under a force f would result in a term f dl being added. If a quantity of charge −de is acquired by a system at an electrical potential Ψ, the electrical work associated with this is −Ψde, which would be included in the infinitesimal expression. Other work terms are added on per system requirements.[11]
Each quantity in the equations above can be divided by the amount of substance, measured in moles, to form molar Gibbs free energy. The Gibbs free energy is one of the most important thermodynamic functions for the characterization of a system. It is a factor in determining outcomes such as the voltage of an electrochemical cell, and the equilibrium constant for a reversible reaction. In isothermal, isobaric systems, Gibbs free energy can be thought of as a "dynamic" quantity, in that it is a representative measure of the competing effects of the enthalpic[clarification needed] and entropic driving forces involved in a thermodynamic process.
The temperature dependence of the Gibbs energy for an ideal gas is given by the Gibbs–Helmholtz equation and its pressure dependence is given by:
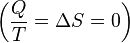 process.
process.
Now consider a subsystem having internal entropy Sint. Such a system is thermally connected to its surroundings, which have entropy Sext. The entropy form of the second law applies only to the closed system formed by both the system and its surroundings. Therefore a process is possible only if
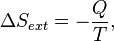 corresponds to the entropy change of the surroundings.
corresponds to the entropy change of the surroundings.
We now have:
If an isolated system (Q = 0) is at constant pressure (Q = ΔH), then
where
All elements in their standard states (diatomic oxygen gas, graphite, etc.) have standard Gibbs free energy change of formation equal to zero, as there is no change involved.
Gibbs energy (also referred to as ∆P) is also the chemical potential that is minimized when a system reaches equilibrium at constant pressure and temperature. Its derivative with respect to the reaction coordinate of the system vanishes at the equilibrium point. As such, it is a convenient criterion for the spontaneity of processes with constant pressure and temperature.
The Gibbs free energy, originally called available energy, was developed in the 1870s by the American mathematician Josiah Willard Gibbs. In 1873, Gibbs described this "available energy" as
the greatest amount of mechanical work which can be obtained from a given quantity of a certain substance in a given initial state, without increasing its total volume or allowing heat to pass to or from external bodies, except such as at the close of the processes are left in their initial condition.[3]The initial state of the body, according to Gibbs, is supposed to be such that "the body can be made to pass from it to states of dissipated energy by reversible processes." In his 1876 magnum opus On the Equilibrium of Heterogeneous Substances, a graphical analysis of multi-phase chemical systems, he engaged his thoughts on chemical free energy in full.
Overview
For systems reacting at STP (or any other fixed temperature and pressure), there is a general natural tendency to achieve a minimum of the free energy.
A quantitative measure of the favorability of a given reaction is the difference ΔG in Gibbs free energy that is (or would be) effected by proceeding with the reaction. When the calculated energetics of the process indicate that ΔG is negative, it means that the reaction will be favoured and will release energy. The energy released equals the maximum amount of work that can be performed as a result of the chemical reaction. In contrast, if conditions indicated a positive ΔG, then energy—in the form of work—would have to be added to the reacting system for the reaction to occur.
The equation can be also seen from the perspective of the system taken together with its surroundings (the rest of the universe). First assume that the given reaction is the only one that is occurring. Then the entropy released or absorbed by the system equals the entropy that the environment must absorb or release, respectively. The reaction will only be allowed if the total entropy change of the universe is zero or positive. This is reflected in a negative ΔG, and the reaction is called exergonic.
If we allow other reactions to occur on the side, then an otherwise endergonic chemical reaction (one with positive ΔG) can be made to happen. The input of heat into an inherently endergonic reaction, such as the elimination of cyclohexanol to cyclohexene, can be seen as coupling an unfavourable reaction (elimination) to a favourable one (burning of coal or other provision of heat) such that the total entropy change of the universe is greater than or equal to zero, making the total Gibbs free energy difference of the coupled reactions negative.
In traditional use, the term "free" was included in "Gibbs free energy" to mean "available in the form of useful work."[2] The characterization becomes more precise if we add the qualification that it is the energy available for non-volume work.[4] (A analogous, but slightly different, meaning of "free" applies in conjunction with the Helmholtz free energy, for systems at constant temperature). However, an increasing number of books and journal articles do not include the attachment "free", referring to G as simply "Gibbs energy". This is the result of a 1988 IUPAC meeting to set unified terminologies for the international scientific community, in which the adjective ‘free’ was supposedly banished.[5][6][7] This standard, however, has not yet been universally adopted.
History
The quantity called "free energy" is a more advanced and accurate replacement for the outdated term affinity, which was used by chemists in previous years[when?] to describe the force that caused chemical reactions.In 1873, Willard Gibbs published A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces, in which he sketched the principles of his new equation that was able to predict or estimate the tendencies of various natural processes to ensue when bodies or systems are brought into contact. By studying the interactions of homogeneous substances in contact, i.e., bodies composed of part solid, part liquid, and part vapor, and by using a three-dimensional volume-entropy-internal energy graph, Gibbs was able to determine three states of equilibrium, i.e., "necessarily stable", "neutral", and "unstable", and whether or not changes would ensue.
Thereafter, in 1882, the German scientist Hermann von Helmholtz characterized the affinity as the largest quantity of work which can be gained when the reaction is carried out in a reversible manner, e.g., electrical work in a reversible cell. The maximum work is thus regarded as the diminution of the free, or available, energy of the system (Gibbs free energy G at T = constant, P = constant or Helmholtz free energy F at T = constant, V = constant), whilst the heat given out is usually a measure of the diminution of the total energy of the system (internal energy). Thus, G or F is the amount of energy "free" for work under the given conditions.
Until this point, the general view had been such that: "all chemical reactions drive the system to a state of equilibrium in which the affinities of the reactions vanish". Over the next 60 years, the term affinity came to be replaced with the term free energy. According to chemistry historian Henry Leicester, the influential 1923 textbook Thermodynamics and the Free Energy of Chemical Substances by Gilbert N. Lewis and Merle Randall led to the replacement of the term "affinity" by the term "free energy" in much of the English-speaking world.
Graphical interpretation
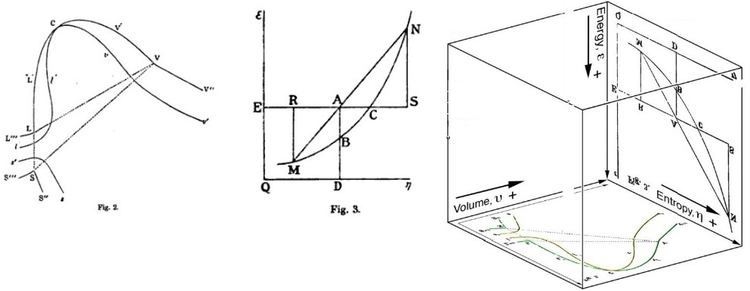
Gibbs free energy was originally defined graphically. In 1873, American engineer Willard Gibbs published his first thermodynamics paper, "Graphical Methods in the Thermodynamics of Fluids", in which Gibbs used the two coordinates of the entropy and volume to represent the state of the body. In his second follow-up paper, "A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces", published later that year, Gibbs added in the third coordinate of the energy of the body, defined on three figures. In 1874, Scottish physicist James Clerk Maxwell used Gibbs' figures to make a 3D energy-entropy-volume thermodynamic surface of a fictitious water-like substance.[8] Thus, in order to understand the very difficult concept of Gibbs free energy one must be able to understand its interpretation as Gibbs defined originally by section AB on his figure 3 and as Maxwell sculpted that section on his 3D surface figure.
American engineer Willard Gibbs' 1873 figures two and three (above left and middle) used by Scottish physicist James Clerk Maxwell in 1874 to create a three-dimensional entropy (x), volume (y), energy (z) thermodynamic surface diagram for a fictitious water-like substance, transposed the two figures of Gibbs (above right) onto the volume-entropy coordinates (transposed to bottom of cube) and energy-entropy coordinates (flipped upside down and transposed to back of cube), respectively, of a three-dimensional Cartesian coordinates; the region AB being the first-ever three-dimensional representation of Gibbs free energy, or what Gibbs called "available energy"; the region AC being its capacity for entropy, what Gibbs defined as "the amount by which the entropy of the body can be increased without changing the energy of the body or increasing its volume.
Definitions

Willard Gibbs’ 1873 available energy (free energy) graph, which shows a plane perpendicular to the axis of v (volume) and passing through point A, which represents the initial state of the body. MN is the section of the surface of dissipated energy. Qε and Qη are sections of the planes η = 0 and ε = 0, and therefore parallel to the axes of ε (internal energy) and η (entropy), respectively. AD and AE are the energy and entropy of the body in its initial state, AB and AC its available energy (Gibbs free energy) and its capacity for entropy (the amount by which the entropy of the body can be increased without changing the energy of the body or increasing its volume) respectively.
- U is the internal energy (SI unit: joule)
- p is pressure (SI unit: pascal)
- V is volume (SI unit: m3)
- T is the temperature (SI unit: kelvin)
- S is the entropy (SI unit: joule per kelvin)
- H is the enthalpy (SI unit: joule)
- μi is the chemical potential of the ith chemical component. (SI unit: joules per particle[9] or joules per mole[2])
- Ni is the number of particles (or number of moles) composing the ith chemical component.
Any number of extra terms may be added, depending on the particular system being considered. Aside from mechanical work, a system may, in addition, perform numerous other types of work. For example, in the infinitesimal expression, the contractile work energy associated with a thermodynamic system that is a contractile fiber that shortens by an amount −dl under a force f would result in a term f dl being added. If a quantity of charge −de is acquired by a system at an electrical potential Ψ, the electrical work associated with this is −Ψde, which would be included in the infinitesimal expression. Other work terms are added on per system requirements.[11]
Each quantity in the equations above can be divided by the amount of substance, measured in moles, to form molar Gibbs free energy. The Gibbs free energy is one of the most important thermodynamic functions for the characterization of a system. It is a factor in determining outcomes such as the voltage of an electrochemical cell, and the equilibrium constant for a reversible reaction. In isothermal, isobaric systems, Gibbs free energy can be thought of as a "dynamic" quantity, in that it is a representative measure of the competing effects of the enthalpic[clarification needed] and entropic driving forces involved in a thermodynamic process.
The temperature dependence of the Gibbs energy for an ideal gas is given by the Gibbs–Helmholtz equation and its pressure dependence is given by:
Derivation
The Gibbs free energy total differential natural variables may be derived via Legendre transforms of the internal energy.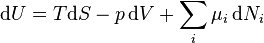 .
.
 .
.
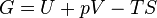 .
.
 .
.
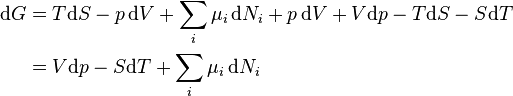 .
.
Homogeneous systems
Because some of the natural variables are intensive, dG may not be integrated using Euler integrals as is the case with internal energy. However, simply substituting the Gibbs-Duhem relation result for U into the definition of G gives a standard expression for G:[12] .
.
Gibbs free energy of reactions
To derive the Gibbs free energy equation for an isolated system, let Stot be the total entropy of the isolated system, that is, a system that cannot exchange energy(heat and work) or mass with its surroundings. According to the second law of thermodynamics: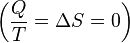 process.
process.Now consider a subsystem having internal entropy Sint. Such a system is thermally connected to its surroundings, which have entropy Sext. The entropy form of the second law applies only to the closed system formed by both the system and its surroundings. Therefore a process is possible only if
 .
.
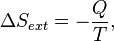 corresponds to the entropy change of the surroundings.
corresponds to the entropy change of the surroundings.We now have:
 (eq.1)
(eq.1)
 favoured reaction (Spontaneous)
favoured reaction (Spontaneous) Neither the forward nor the reverse reaction prevails (Equilibrium)
Neither the forward nor the reverse reaction prevails (Equilibrium) disfavoured reaction (Nonspontaneous)
disfavoured reaction (Nonspontaneous)
 (eq.2)
(eq.2)
If an isolated system (Q = 0) is at constant pressure (Q = ΔH), then
Useful identities
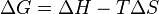 (for constant temperature)
(for constant temperature) (for a system at equilibrium)
(for a system at equilibrium) (see Chemical equilibrium)
(see Chemical equilibrium)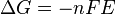

where
- ΔG = change in Gibbs free energy
- ΔH = change in enthalpy
- T = absolute temperature
- ΔS = change in entropy
- R = gas constant
- ln = natural logarithm
- ΔrG = change of reaction in Gibbs free energy
- ΔrG° = standard change of reaction in Gibbs free energy
- K = equilibrium constant
- Qr = reaction quotient
- n = number of electrons per mole product
- F = Faraday constant (coulombs per mole)
- E = electrode potential of the reaction
Gibbs free energy, the second law of thermodynamics, and metabolism
A chemical reaction will (or can) proceed spontaneously if the change in the total entropy of the universe that would be caused by the reaction is nonnegative. As discussed in the overview, if the temperature and pressure are held constant, the Gibbs free energy is a (negative) proxy for the change in total entropy of the universe. It's "negative" because S appears with a negative coefficient in the expression for G, so the Gibbs free energy moves in the opposite direction from the total entropy. Thus, a reaction with a positive Gibbs free energy will not proceed spontaneously. However, in biological systems (among others), energy inputs from other energy sources (including the sun and exothermic chemical reactions) are "coupled" with reactions that are not entropically favored (i.e. have a Gibbs free energy above zero). Taking into account the coupled reactions, the total entropy in the universe increases. This coupling allows endergonic reactions, such as photosynthesis and DNA synthesis, to proceed without decreasing the total entropy of the universe. Thus biological systems do not violate the second law of thermodynamics.Standard energy change of formation
The standard Gibbs free energy of formation of a compound is the change of Gibbs free energy that accompanies the formation of 1 mole of that substance from its component elements, at their standard states (the most stable form of the element at 25 degrees Celsius and 101.3 kilopascals). Its symbol is ΔfG˚.All elements in their standard states (diatomic oxygen gas, graphite, etc.) have standard Gibbs free energy change of formation equal to zero, as there is no change involved.
- ΔfG = ΔfG˚ + RT ln Qf ; Qf is the reaction quotient.
Table of selected substances[14]
| Substance | State | ΔfG°(kJ/mol) | ΔfG°(kcal/mol) |
|---|---|---|---|
| NO | g | -87.6 | -20.9 |
| NO2 | g | -51.3 | -12.3 |
| N2O | g | -103.7 | -24.78 |
| H2O | g | -228.6 | −54.64 |
| H2O | l | -237.1 | −56.67 |
| CO2 | g | -394.4 | −94.26 |
| CO | g | -137.2 | −32.79 |
| CH4 | g | -50.5 | −12.1 |
| C2H6 | g | -32.0 | −7.65 |
| C3H8 | g | -23.4 | −5.59 |
| C6H6 | g | -129.7 | -29.76 |
| C6H6 | l | -124.5 | -31.00 |




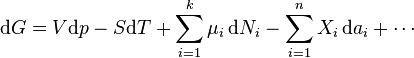


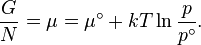
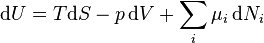 .
. .
.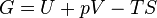 .
. .
.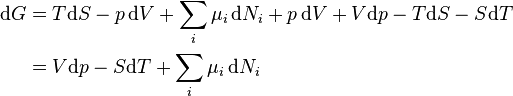 .
. .
.
 .
.



 (eq.1)
(eq.1) favoured reaction (Spontaneous)
favoured reaction (Spontaneous) Neither the forward nor the reverse reaction prevails (
Neither the forward nor the reverse reaction prevails ( disfavoured reaction (Nonspontaneous)
disfavoured reaction (Nonspontaneous) (eq.2)
(eq.2)

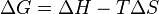 (for constant temperature)
(for constant temperature) (for a system at equilibrium)
(for a system at equilibrium) (see
(see 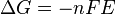









 of an atmospheric
of an atmospheric  (in kg) of X in the box to its removal rate, which is the sum of the flow of X out of the box (
(in kg) of X in the box to its removal rate, which is the sum of the flow of X out of the box ( ), chemical loss of X (
), chemical loss of X ( ), and
), and  ) (all in kg/s):
) (all in kg/s):  .
.