
A conventional
crystalline silicon solar cell. Electrical contacts made from
busbars (the larger strips) and fingers (the smaller ones) are printed on the silicon
wafer.
A
solar cell, or
photovoltaic cell, is an electrical device that converts the energy of
light directly into
electricity by the
photovoltaic effect, which is a
physical and
chemical phenomenon.
[1] It is a form of photoelectric cell, defined as a device whose electrical characteristics, such as current, voltage, or resistance, vary when exposed to light. Solar cells are the building blocks of photovoltaic modules, otherwise known as
solar panels.
Solar cells are described as being
photovoltaic irrespective of whether the source is
sunlight or an artificial light. They are used as a
photodetector (for example
infrared detectors), detecting light or other
electromagnetic radiation near the visible range, or measuring light intensity.
The operation of a photovoltaic (PV) cell requires 3 basic attributes:
- The absorption of light, generating either electron-hole pairs or excitons.
- The separation of charge carriers of opposite types.
- The separate extraction of those carriers to an external circuit.
In contrast, a
solar thermal collector supplies heat by absorbing sunlight, for the purpose of either direct heating or indirect electrical power generation from heat. A "photoelectrolytic cell" (
photoelectrochemical cell), on the other hand, refers either to a type of photovoltaic cell (like that developed by
Edmond Becquerel and modern
dye-sensitized solar cells), or to a device that splits water directly into hydrogen and oxygen using only solar illumination.
Applications
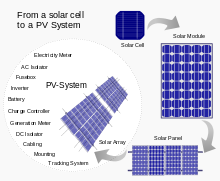
Assemblies of solar cells are used to make
solar modules which generate electrical power from
sunlight, as distinguished from a "solar thermal module" or "solar hot water panel". A solar array generates
solar power using
solar energy.
Cells, modules, panels and systems
Multiple solar cells in an integrated group, all oriented in one plane, constitute a solar photovoltaic panel or solar photovoltaic module. Photovoltaic modules often have a sheet of glass on the sun-facing side, allowing light to pass while protecting the semiconductor
wafers. Solar cells are usually connected in
series in modules, creating an additive
voltage. Connecting cells in parallel yields a higher current; however, problems such as shadow effects can shut down the weaker (less illuminated) parallel string (a number of series connected cells) causing substantial power loss and possible damage because of the
reverse bias applied to the shadowed cells by their illuminated partners. Strings of series cells are usually handled independently and not connected in parallel, though (as of 2014) individual
power boxes are often supplied for each module, and are connected in parallel. Although modules can be interconnected to create an array with the desired peak DC voltage and loading current capacity, using independent MPPTs (
maximum power point trackers) is preferable. Otherwise, shunt
diodes can reduce shadowing power loss in arrays with series/parallel connected cells.
[citation needed]
Typical PV system prices in 2013 in selected countries (USD)
| USD/W |
Australia |
China |
France |
Germany |
Italy |
Japan |
United Kingdom |
United States |
| Residential |
1.8 |
1.5 |
4.1 |
2.4 |
2.8 |
4.2 |
2.8 |
4.9 |
| Commercial |
1.7 |
1.4 |
2.7 |
1.8 |
1.9 |
3.6 |
2.4 |
4.5 |
| Utility-scale |
2.0 |
1.4 |
2.2 |
1.4 |
1.5 |
2.9 |
1.9 |
3.3 |
Source: IEA – Technology Roadmap: Solar Photovoltaic Energy report, 2014 edition[2]:15
Note: DOE – Photovoltaic System Pricing Trends reports lower prices for the U.S.[3] |
History
The
photovoltaic effect was experimentally demonstrated first by French physicist
Edmond Becquerel. In 1839, at age 19, he built the world's first photovoltaic cell in his father's laboratory.
Willoughby Smith first described the "Effect of Light on Selenium during the passage of an Electric Current" in a 20 February 1873 issue of
Nature. In 1883
Charles Fritts built the first
solid state photovoltaic cell by coating the
semiconductor selenium with a thin layer of
gold to form the junctions; the device was only around 1% efficient.
In 1888 Russian physicist
Aleksandr Stoletov built the first cell based on the outer
photoelectric effect discovered by
Heinrich Hertz in 1887.
[4]
In 1905
Albert Einstein proposed a new quantum theory of light and explained the
photoelectric effect in a landmark paper, for which he received the
Nobel Prize in Physics in 1921.
[5]
Vadim Lashkaryov discovered
p-
n-junctions in Cu

O and silver sulphide protocells in 1941.
[6]
Russell Ohl patented the modern junction semiconductor solar cell in 1946
[7] while working on the series of advances that would lead to the
transistor.
The first practical photovoltaic cell was publicly demonstrated on 25 April 1954 at
Bell Laboratories.
[8] The inventors were Daryl Chapin,
Calvin Souther Fuller and
Gerald Pearson.
[9]
Solar cells gained prominence with their incorporation onto the 1958
Vanguard I satellite.
Improvements were gradual over the next two decades. However, this success was also the reason that costs remained high, because space users were willing to pay for the best possible cells, leaving no reason to invest in lower-cost, less-efficient solutions. The price was determined largely by the semiconductor industry; their move to
integrated circuits in the 1960s led to the availability of larger
boules at lower relative prices. As their price fell, the price of the resulting cells did as well. These effects lowered 1971 cell costs to some $100 per watt.
Space Applications
Solar cells were first used in a prominent application when they were proposed and flown on the Vanguard satellite in 1958, as an alternative power source to the
primary battery power source. By adding cells to the outside of the body, the mission time could be extended with no major changes to the spacecraft or its power systems. In 1959 the United States launched
Explorer 6, featuring large wing-shaped solar arrays, which became a common feature in satellites. These arrays consisted of 9600
Hoffman solar cells.
By the 1960s, solar cells were (and still are) the main power source for most Earth orbiting satellites and a number of probes into the solar system, since they offered the best
power-to-weight ratio. However, this success was possible because in the space application, power system costs could be high, because space users had few other power options, and were willing to pay for the best possible cells. The space power market drove the development of higher efficiencies in solar cells up until the
National Science Foundation "Research Applied to National Needs" program began to push development of solar cells for terrestrial applications.
In the early 1990s the technology used for space solar cells diverged from the silicon technology used for terrestrial panels, with the spacecraft application shifting to
gallium arsenide-based III-V semiconductor materials, which then evolved into the modern III-V
multijunction photovoltaic cell used on spacecraft.
Price reductions

Dr. Elliot Berman testing various solar arrays manufactured by his company, Solar Power Corporation.
In late 1969 Elliot Berman joined the
Exxon's task force which was looking for projects 30 years in the future and in April 1973 he founded Solar Power Corporation, a wholly owned subsidiary of Exxon that time.
[12][13] The group had concluded that electrical power would be much more expensive by 2000, and felt that this increase in price would make alternative energy sources more attractive. He conducted a market study and concluded that a
price per watt of about $20/watt would create significant demand. The team eliminated the steps of polishing the wafers and coating them with an anti-reflective layer, relying on the rough-sawn wafer surface. The team also replaced the expensive materials and hand wiring used in space applications with a
printed circuit board on the back,
acrylic plastic on the front, and
silicone glue between the two, "potting" the cells. Solar cells could be made using cast-off material from the electronics market. By 1973 they announced a product, and SPC convinced
Tideland Signal to use its panels to power navigational
buoys, initially for the U.S. Coast Guard.
[12]
Research into solar power for terrestrial applications became prominent with the U.S. National Science Foundation's Advanced Solar Energy Research and Development Division within the "Research Applied to National Needs" program, which ran from 1969 to 1977,
[15] and funded research on developing solar power for ground electrical power systems. A 1973 conference, the "Cherry Hill Conference", set forth the technology goals required to achieve this goal and outlined an ambitious project for achieving them, kicking off an applied research program that would be ongoing for several decades.
[16] The program was eventually taken over by the
Energy Research and Development Administration (ERDA),
[17] which was later merged into the
U.S. Department of Energy.
Following the
1973 oil crisis oil companies used their higher profits to start (or buy) solar firms, and were for decades the largest producers. Exxon, ARCO, Shell, Amoco (later purchased by BP) and Mobil all had major solar divisions during the 1970s and 1980s. Technology companies also participated, including General Electric, Motorola, IBM, Tyco and RCA.
[18]
Declining costs and exponential growth
Swanson's law is an observation similar to
Moore's Law that states that solar cell prices fall 20% for every doubling of industry capacity. It was featured in an article in the British weekly newspaper
The Economist.
[19]
Further improvements reduced production cost to under $1 per watt, with wholesale costs well under $2.
Balance of system costs were then higher than the panels. Large commercial arrays could be built, as of 2010, at below $3.40 a watt, fully commissioned.
[20][21]
As the semiconductor industry moved to ever-larger
boules, older equipment became inexpensive. Cell sizes grew as equipment became available on the surplus market; ARCO Solar's original panels used cells 2 to 4 inches (50 to 100 mm) in diameter. Panels in the 1990s and early 2000s generally used 125 mm wafers; since 2008 almost all new panels use 150 mm cells. The widespread introduction of
flat screen televisions in the late 1990s and early 2000s led to the wide availability of large, high-quality glass sheets to cover the panels.
During the 1990s,
polysilicon ("poly") cells became increasingly popular. These cells offer less efficiency than their monosilicon ("mono") counterparts, but they are grown in large vats that reduce cost. By the mid-2000s, poly was dominant in the low-cost panel market, but more recently the mono returned to widespread use.
Manufacturers of wafer-based cells responded to high silicon prices in 2004–2008 with rapid reductions in silicon consumption. In 2008, according to Jef Poortmans, director of
IMEC's organic and solar department, current cells use 8–9 grams (0.28–0.32 oz) of silicon per watt of power generation, with wafer thicknesses in the neighborhood of 200
microns.
First Solar is the largest
thin film manufacturer in the world, using a
CdTe-cell sandwiched between two layers of glass.
Crystalline silicon panels dominate worldwide markets and are mostly manufactured in China and Taiwan. By late 2011, a drop in European demand due to budgetary turmoil dropped prices for crystalline solar modules to about $1.09
[21] per watt down sharply from 2010. Prices continued to fall in 2012, reaching $0.62/watt by 4Q2012.
[22]
Global installed PV capacity reached at least 177 gigawatts in 2014, enough to supply 1 percent of the world's total electricity consumption. Solar PV is growing fastest in Asia, with China and Japan currently accounting for half of
worldwide deployment.
[23]
Subsidies and grid parity
The price of solar panels fell steadily for 40 years, interrupted in 2004 when high subsidies in Germany drastically increased demand there and greatly increased the price of purified silicon (which is used in computer chips as well as solar panels). The
recession of 2008 and the onset of Chinese manufacturing caused prices to resume their decline. In the four years after January 2008 prices for solar modules in Germany dropped from €3 to €1 per peak watt. During that same time production capacity surged with an annual growth of more than 50%. China increased market share from 8% in 2008 to over 55% in the last quarter of 2010.
[28] In December 2012 the price of Chinese solar panels had dropped to $0.60/Wp (crystalline modules).
[29]
Theory
The solar cell works in several steps:
- Photons in sunlight hit the solar panel and are absorbed by semiconducting materials, such as silicon.
- Electrons and protons are excited from their current molecular/atomic orbital. Once excited an electron can either dissipate the energy as heat and return to its orbital or travel through the cell until it reaches an electrode. Current flows through the material to cancel the potential and this electricity is captured. The chemical bonds of the material are vital for this process to work, and usually silicon is used in two layers, one layer being bonded with boron, the other phosphorus. These layers have different chemical electric charges and subsequently both drive and direct the current of electrons.[1]
- An array of solar cells converts solar energy into a usable amount of direct current (DC) electricity.
- An inverter can convert the power to alternating current (AC).
The most commonly known solar cell is configured as a large-area
p-n junction made from silicon.
Efficiency

The
Shockley-Queisser limit for the theoretical maximum efficiency of a solar cell. Semiconductors with
band gap between 1 and 1.5
eV, or near-infrared light, have the greatest potential to form an efficient single-junction cell. (The efficiency "limit" shown here can be exceeded by
multijunction solar cells.)
Solar cell efficiency may be broken down into reflectance efficiency, thermodynamic efficiency, charge carrier separation efficiency and conductive efficiency. The overall efficiency is the product of these individual metrics.
A solar cell has a voltage dependent efficiency curve, temperature coefficients, and allowable shadow angles.
Due to the difficulty in measuring these parameters directly, other parameters are substituted: thermodynamic efficiency,
quantum efficiency,
integrated quantum efficiency, V
OC ratio, and fill factor. Reflectance losses are a portion of quantum efficiency under "external quantum efficiency". Recombination losses make up another portion of quantum efficiency, V
OC ratio, and fill factor. Resistive losses are predominantly categorized under fill factor, but also make up minor portions of quantum efficiency, V
OC ratio.
The fill factor is the ratio of the actual maximum obtainable
power to the product of the
open circuit voltage and
short circuit current. This is a key parameter in evaluating performance. In 2009, typical commercial solar cells had a fill factor > 0.70. Grade B cells were usually between 0.4 to 0.7.
[30] Cells with a high fill factor have a low
equivalent series resistance and a high
equivalent shunt resistance, so less of the current produced by the cell is dissipated in internal losses.
Single p–n junction crystalline silicon devices are now approaching the theoretical limiting power efficiency of 33.7%, noted as the
Shockley–Queisser limit in 1961. In the extreme, with an infinite number of layers, the corresponding limit is 86% using concentrated sunlight.
[31]
In December 2014, a solar cell achieved a new laboratory record with 46 percent efficiency in a French-German collaboration.
[32]
In 2014, three companies broke the record of 25.6% for a silicon solar cell. Panasonic's was the most efficient. The company moved the front contacts to the rear of the panel, eliminating shaded areas. In addition they applied thin silicon films to the (high quality silicon) wafer's front and back to eliminate defects at or near the wafer surface.
[33]
In September 2015, the
Fraunhofer Institute for
Solar Energy Systems (Fraunhofer ISE) announced the achievement of an efficiency above 20% for
epitaxial wafer cells. The work on optimizing the atmospheric-pressure
chemical vapor deposition (APCVD) in-line production chain was done in collaboration with NexWafe GmbH, a company spun off from Fraunhofer ISE to commercialize production.
[34]
For triple-junction thin-film solar cells, the world record is 13.6%, set in June 2015.
[35]
Materials
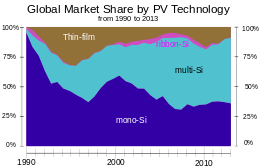
Global market-share in terms of annual production by PV technology since 1990
Solar cells are typically named after the
semiconducting material they are made of. These
materials must have certain characteristics in order to absorb
sunlight. Some cells are designed to handle sunlight that reaches the Earth's surface, while others are optimized for
use in space. Solar cells can be made of only one single layer of light-absorbing material (
single-junction) or use multiple physical configurations (
multi-junctions) to take advantage of various absorption and charge separation mechanisms.
Solar cells can be classified into first, second and third generation cells. The first generation cells—also called conventional, traditional or
wafer-based cells—are made of
crystalline silicon, the commercially predominant PV technology, that includes materials such as
polysilicon and
monocrystalline silicon. Second generation cells are
thin film solar cells, that include
amorphous silicon,
CdTe and
CIGS cells and are commercially significant in utility-scale
photovoltaic power stations,
building integrated photovoltaics or in small
stand-alone power system. The third generation of solar cells includes a number of thin-film technologies often described as emerging photovoltaics—most of them have not yet been commercially applied and are still in the research or development phase. Many use organic materials, often
organometallic compounds as well as inorganic substances. Despite the fact that their efficiencies had been low and the stability of the absorber material was often too short for commercial applications, there is a lot of research invested into these technologies as they promise to achieve the goal of producing low-cost, high-efficiency solar cells.
Crystalline silicon
By far, the most prevalent bulk material for solar cells is
crystalline silicon (c-Si), also known as "solar grade silicon". Bulk silicon is separated into multiple categories according to crystallinity and crystal size in the resulting
ingot,
ribbon or
wafer. These cells are entirely based around the concept of a
p-n junction. Solar cells made of c-Si are made from
wafers between 160 to 240
micrometers thick.
Monocrystalline silicon
Monocrystalline silicon (mono-Si) solar cells are more efficient and more expensive than most other types of cells. The corners of the cells look clipped, like an octagon, because the wafer material is cut from cylindrical ingots, that are typically grown by the
Czochralski process. Solar panels using mono-Si cells display a distinctive pattern of small white diamonds.
Epitaxial silicon
Epitaxial wafers can be grown on a monocrystalline silicon "seed" wafer by atmospheric-pressure CVD in a high-throughput inline process, and then detached as self-supporting wafers of some standard thickness (e.g., 250 µm) that can be manipulated by hand, and directly substituted for wafer cells cut from monocrystalline silicon ingots. Solar cells made with this technique can have efficiencies approaching those of wafer-cut cells, but at appreciably lower cost.
[36]
Polycrystalline silicon
Polycrystalline silicon, or multicrystalline silicon (multi-Si) cells are made from cast square ingots—large blocks of molten silicon carefully cooled and solidified. They consist of small crystals giving the material its typical
metal flake effect. Polysilicon cells are the most common type used in photovoltaics and are less expensive, but also less efficient, than those made from monocrystalline silicon.
Ribbon silicon
Ribbon silicon is a type of polycrystalline silicon—it is formed by drawing flat thin films from
molten silicon and results in a polycrystalline structure. These cells are cheaper to make than multi-Si, due to a great reduction in silicon waste, as this approach does not require
sawing from
ingots.
[37] However, they are also less efficient.
Mono-like-multi silicon (MLM)
This form was developed in the 2000s and introduced commercially around 2009. Also called cast-mono, this design uses polycrystalline casting chambers with small "seeds" of mono material. The result is a bulk mono-like material that is polycrystalline around the outsides. When sliced for processing, the inner sections are high-efficiency mono-like cells (but square instead of "clipped"), while the outer edges are sold as conventional poly. This production method results in mono-like cells at poly-like prices.
[38]
Thin film
Thin-film technologies reduce the amount of active material in a cell. Most designs sandwich active material between two panes of glass. Since silicon solar panels only use one pane of glass, thin film panels are approximately twice as heavy as crystalline silicon panels, although they have a smaller ecological impact (determined from
life cycle analysis).
[39] The majority of film panels have 2-3 percentage points lower conversion efficiencies than crystalline silicon.
[40] Cadmium telluride (CdTe),
copper indium gallium selenide (CIGS) and
amorphous silicon (a-Si) are three thin-film technologies often used for outdoor applications. As of December 2013, CdTe cost per installed watt was $0.59 as reported by First Solar. CIGS technology laboratory demonstrations reached 20.4% conversion efficiency as of December 2013. The lab efficiency of GaAs thin film technology topped 28%.
[citation needed] The
quantum efficiency of thin film solar cells is also lower due to reduced number of collected charge carriers per incident photon. Most recently, CZTS solar cell emerge as the less-toxic thin film solar cell technology, which achieved ~12% efficiency.
[41] Thin film solar cells are increasing due to it being silent, renewable and solar energy being the most abundant energy source on Earth.
[42]
Cadmium telluride
Cadmium telluride is the only thin film material so far to rival crystalline silicon in cost/watt. However cadmium is highly toxic and
tellurium (
anion: "telluride") supplies are limited. The
cadmium present in the cells would be toxic if released. However, release is impossible during normal operation of the cells and is unlikely during fires in residential roofs.
[43] A square meter of CdTe contains approximately the same amount of Cd as a single C cell
nickel-cadmium battery, in a more stable and less soluble form.
[43]
Copper indium gallium selenide
Copper indium gallium selenide (CIGS) is a
direct band gap material. It has the highest efficiency (~20%) among all commercially significant thin film materials (see
CIGS solar cell). Traditional methods of fabrication involve vacuum processes including co-evaporation and sputtering. Recent developments at
IBM and
Nanosolar attempt to lower the cost by using non-vacuum solution processes.
[44]
Silicon thin film
Silicon thin-film cells are mainly deposited by
chemical vapor deposition (typically plasma-enhanced, PE-CVD) from
silane gas and
hydrogen gas. Depending on the deposition parameters, this can yield
amorphous silicon (a-Si or a-Si:H),
protocrystalline silicon or
nanocrystalline silicon (nc-Si or nc-Si:H), also called microcrystalline silicon.
[45]
Amorphous silicon is the most well-developed thin film technology to-date. An amorphous silicon (a-Si) solar cell is made of non-crystalline or microcrystalline silicon. Amorphous silicon has a higher bandgap (1.7 eV) than crystalline silicon (c-Si) (1.1 eV), which means it absorbs the visible part of the solar spectrum more strongly than the higher power density
infrared portion of the spectrum. The production of a-Si thin film solar cells uses glass as a substrate and deposits a very thin layer of silicon by
plasma-enhanced chemical vapor deposition (PECVD).
Protocrystalline silicon with a low volume fraction of nanocrystalline silicon is optimal for high open circuit voltage.
[46] Nc-Si has about the same bandgap as c-Si and nc-Si and a-Si can advantageously be combined in thin layers, creating a layered cell called a tandem cell. The top cell in a-Si absorbs the visible light and leaves the infrared part of the spectrum for the bottom cell in nc-Si.
Gallium arsenide thin filmT
The semiconductor material
Gallium arsenide (GaAs) is also used for single-crystalline thin film solar cells. Although GaAs cells are very expensive, they hold the world's record in efficiency for a
single-junction solar cell at 28.8%.
[47] GaAs is more commonly used in
multijunction photovoltaic cells for
concentrated photovoltaics (CPV, HCPV) and for
solar panels on spacecrafts, as the industry favours efficiency over cost for
space-based solar power.
Multijunction cells

Dawn's 10
kW triple-junction gallium arsenide solar array at full extension
Multi-junction cells consist of multiple thin films, each essentially a solar cell grown on top of each other, typically using
metalorganic vapour phase epitaxy. Each layers has a different band gap energy to allow it to absorb
electromagnetic radiation over a different portion of the spectrum. Multi-junction cells were originally developed for special applications such as
satellites and
space exploration, but are now used increasingly in terrestrial
concentrator photovoltaics (CPV), an emerging technology that uses lenses and curved mirrors to concentrate sunlight onto small but highly efficient multi-junction solar cells. By concentrating sunlight up to a thousand times,
High concentrated photovoltaics (HCPV) has the potential to outcompete conventional solar PV in the future.
[48]:21,26
Tandem solar cells based on monolithic, series connected, gallium indium phosphide (GaInP), gallium arsenide (GaAs), and germanium (Ge) p–n junctions, are increasing sales, despite cost pressures.
[49] Between December 2006 and December 2007, the cost of 4N gallium metal rose from about $350 per kg to $680 per kg. Additionally, germanium metal prices have risen substantially to $1000–1200 per kg this year. Those materials include gallium (4N, 6N and 7N Ga), arsenic (4N, 6N and 7N) and germanium, pyrolitic boron nitride (pBN) crucibles for growing crystals, and boron oxide, these products are critical to the entire substrate manufacturing industry.
[citation needed]
A triple-junction cell, for example, may consist of the semiconductors:
GaAs,
Ge, and
GaInP
2.
[50] Triple-junction GaAs solar cells were used as the power source of the Dutch four-time
World Solar Challenge winners
Nuna in 2003, 2005 and 2007 and by the Dutch solar cars
Solutra (2005),
Twente One (2007) and 21Revolution (2009).
[citation needed] GaAs based multi-junction devices are the most efficient solar cells to date. On 15 October 2012, triple junction metamorphic cells reached a record high of 44%.
[51]
Research in solar cells
Perovskite solar cells
Perovskite solar cells are solar cells that include a
perovskite-structured material as the active layer. Most commonly, this is a solution-processed hybrid organic-inorganic tin or lead halide based material. Efficiencies have increased from below 10% at their first usage in 2009 to over 20% in 2014, making them a very rapidly advancing technology and a hot topic in the solar cell field.
[52] Perovskite solar cells are also forecast to be extremely cheap to scale up, making them a very attractive option for commercialisation.
Liquid inks
In 2014, researchers at
California NanoSystems Institute discovered using
kesterite and
perovskite improved
electric power conversion efficiency for solar cells.
[53]
Upconversion and Downconversion
Photon upconversion is the process of using two low-energy (
e.g., infrared) photons to produce one higher energy photon;
downconversion is the process of using one high energy photon (
e.g.,, ultraviolet) to produce two lower energy photons. Either of these techniques could be used to produce higher efficiency solar cells by allowing solar photons to be more efficiently used. The difficulty, however, is that the conversion efficiency of existing
phosphors exhibiting up- or down-conversion is low, and is typically narrow band.
One upconversion technique is to incorporate
lanthanide-doped materials (
Er3+,
Yb3+,
Ho3+ or a combination), taking advantage of their
luminescence to convert
infrared radiation to visible light. Upconversion process occurs when two
infrared photons are absorbed by
rare-earth ions to generate a (high-energy) absorbable photon. As example, the energy transfer upconversion process (ETU), consists in successive transfer processes between excited ions in the near infrared. The upconverter material could be placed below the solar cell to absorb the infrared light that passes through the silicon. Useful ions are most commonly found in the trivalent state.
Er+ ions have been the most used.
Er3+ ions absorb solar radiation around 1.54 µm. Two
Er3+ ions that have absorbed this radiation can interact with each other through an upconversion process. The excited ion emits light above the Si bandgap that is absorbed by the solar cell and creates an additional electron–hole pair that can generate current. However, the increased efficiency was small. In addition, fluoroindate glasses have low
phonon energy and have been proposed as suitable matrix doped with
Ho3+ ions.
[54]
Light-absorbing dyes
Dye-sensitized solar cells (DSSCs) are made of low-cost materials and do not need elaborate manufacturing equipment, so they can be made in a
DIY fashion. In bulk it should be significantly less expensive than older
solid-state cell designs. DSSC's can be engineered into flexible sheets and although its
conversion efficiency is less than the best
thin film cells, its
price/performance ratio may be high enough to allow them to compete with
fossil fuel electrical generation.
Typically a
ruthenium metalorganic dye (Ru-centered) is used as a
monolayer of light-absorbing material. The dye-sensitized solar cell depends on a
mesoporous layer of
nanoparticulate titanium dioxide to greatly amplify the surface area (200–300 m
2/g
TiO
2, as compared to approximately 10 m
2/g of flat single crystal). The photogenerated electrons from the light absorbing dye are passed on to the n-type
TiO
2 and the holes are absorbed by an
electrolyte on the other side of the dye. The circuit is completed by a
redox couple in the electrolyte, which can be liquid or solid. This type of cell allows more flexible use of materials and is typically manufactured by
screen printing or
ultrasonic nozzles, with the potential for lower processing costs than those used for bulk solar cells. However, the dyes in these cells also suffer from
degradation under heat and
UV light and the cell casing is difficult to
seal due to the solvents used in assembly. The first commercial shipment of DSSC solar modules occurred in July 2009 from G24i Innovations.
[55]
Quantum dots
Quantum dot solar cells (QDSCs) are based on the Gratzel cell, or
dye-sensitized solar cell architecture, but employ low
band gap semiconductor nanoparticles, fabricated with crystallite sizes small enough to form
quantum dots (such as
CdS,
CdSe,
Sb
2S
3,
PbS, etc.), instead of organic or organometallic dyes as light absorbers. QD's size quantization allows for the band gap to be tuned by simply changing particle size. They also have high
extinction coefficients and have shown the possibility of
multiple exciton generation.
[56]
In a QDSC, a
mesoporous layer of
titanium dioxide nanoparticles forms the backbone of the cell, much like in a DSSC. This
TiO
2 layer can then be made photoactive by coating with semiconductor quantum dots using
chemical bath deposition,
electrophoretic deposition or successive ionic layer adsorption and reaction. The electrical circuit is then completed through the use of a liquid or solid
redox couple. The efficiency of QDSCs has increased
[57] to over 5% shown for both liquid-junction
[58] and solid state cells.
[59] In an effort to decrease production costs, the
Prashant Kamat research group
[60] demonstrated a solar paint made with
TiO
2 and CdSe that can be applied using a one-step method to any conductive surface with efficiencies over 1%.
[61]
Organic/polymer solar cells
Organic solar cells and
polymer solar cells are built from thin films (typically 100 nm) of
organic semiconductors including polymers, such as
polyphenylene vinylene and small-molecule compounds like copper phthalocyanine (a blue or green organic pigment) and
carbon fullerenes and fullerene derivatives such as
PCBM.
They can be processed from liquid solution, offering the possibility of a simple roll-to-roll printing process, potentially leading to inexpensive, large-scale production. In addition, these cells could be beneficial for some applications where mechanical flexibility and disposability are important. Current cell efficiencies are, however, very low, and practical devices are essentially non-existent.
Energy conversion efficiencies achieved to date using conductive polymers are very low compared to inorganic materials. However,
Konarka Power Plastic reached efficiency of 8.3%
[62] and organic tandem cells in 2012 reached 11.1%.
[citation needed]
The active region of an organic device consists of two materials, one electron donor and one electron acceptor. When a photon is converted into an electron hole pair, typically in the donor material, the charges tend to remain bound in the form of an
exciton, separating when the exciton diffuses to the donor-acceptor interface, unlike most other solar cell types. The short exciton diffusion lengths of most polymer systems tend to limit the efficiency of such devices. Nanostructured interfaces, sometimes in the form of bulk heterojunctions, can improve performance.
[63]
In 2011, MIT and Michigan State researchers developed solar cells with a power efficiency close to 2% with a transparency to the human eye greater than 65%, achieved by selectively absorbing the ultraviolet and near-infrared parts of the spectrum with small-molecule compounds.
[64][65] Researchers at UCLA more recently developed an analogous polymer solar cell, following the same approach, that is 70% transparent and has a 4% power conversion efficiency.
[66][67][68] These lightweight, flexible cells can be produced in bulk at a low cost and could be used to create power generating windows.
In 2013, researchers announced
polymer cells with some 3% efficiency. They used
block copolymers, self-assembling organic materials that arrange themselves into distinct layers. The research focused on P3HT-b-PFTBT that separates into bands some 16 nanometers wide.
[69][70]
Adaptive cells
Adaptive cells change their absorption/reflection characteristics depending to respond to environmental conditions. An adaptive material responds to the intensity and angle of incident light. At the part of the cell where the light is most intense, the cell surface changes from reflective to adaptive, allowing the light to penetrate the cell. The other parts of the cell remain reflective increasing the retention of the absorbed light within the cell.
[71]
In 2014 a system that combined an adaptive surface with a glass substrate that redirect the absorbed to a light absorber on the edges of the sheet. The system also included an array of fixed lenses/mirrors to concentrate light onto the adaptive surface. As the day continues, the concentrated light moves along the surface of the cell. That surface switches from reflective to adaptive when the light is most concentrated and back to reflective after the light moves along.
[71]
Manufacture
Solar cells share some of the same processing and manufacturing techniques as other semiconductor devices. However, the stringent requirements for cleanliness and quality control of semiconductor fabrication are more relaxed for solar cells, lowering costs.
Polycrystalline silicon wafers are made by wire-sawing block-cast silicon ingots into 180 to 350 micrometer wafers. The wafers are usually lightly
p-type-doped. A surface diffusion of
n-type dopants is performed on the front side of the wafer. This forms a p–n junction a few hundred nanometers below the surface.
Anti-reflection coatings are then typically applied to increase the amount of light coupled into the solar cell.
Silicon nitride has gradually replaced titanium dioxide as the preferred material, because of its excellent surface passivation qualities. It prevents carrier recombination at the cell surface. A layer several hundred nanometers thick is applied using PECVD. Some solar cells have textured front surfaces that, like anti-reflection coatings, increase the amount of light reaching the wafer. Such surfaces were first applied to single-crystal silicon, followed by multicrystalline silicon somewhat later.
A full area metal contact is made on the back surface, and a grid-like metal contact made up of fine "fingers" and larger "bus bars" are screen-printed onto the front surface using a
silver paste. This is an evolution of the so-called "wet" process for applying electrodes, first described in a US patent filed in 1981 by
Bayer AG.
[72] The rear contact is formed by screen-printing a metal paste, typically aluminium. Usually this contact covers the entire rear, though some designs employ a grid pattern. The paste is then fired at several hundred degrees Celsius to form metal electrodes in
ohmic contact with the silicon. Some companies use an additional electro-plating step to increase efficiency. After the metal contacts are made, the solar cells are interconnected by flat wires or metal ribbons, and assembled into
modules or "solar panels". Solar panels have a sheet of
tempered glass on the front, and a
polymer encapsulation on the back.
Manufacturers and certification

Solar cell production by region
[73]
National Renewable Energy Laboratory tests and validates solar technologies. Three reliable groups certify solar equipment:
UL and
IEEE (both U.S. standards) and
IEC.
Solar cells are manufactured in volume in Japan, Germany, China, Taiwan, Malaysia and the United States, whereas Europe, China, the U.S., and Japan have dominated (94% or more as of 2013) in installed systems.
[74] Other nations are acquiring significant solar cell production capacity.
Global PV cell/module production increased by 10% in 2012 despite a 9% decline in solar energy investments according to the annual "PV Status Report" released by the
European Commission's Joint Research Centre. Between 2009 and 2013 cell production has quadrupled.
[74][75][76]
China
Due to heavy government investment, China has become the dominant force in solar cell manufacturing. Chinese companies produced solar cells/modules with a capacity of ~23 GW in 2013 (60% of global production).
[74]
Malaysia
In 2014, Malaysia was the world's third largest manufacturer of
photovoltaics equipment, behind
China and the
European Union.
[77]
United States
Solar cell production in the U.S. has suffered due to the
global financial crisis, but recovered partly due to the falling price of quality silicon.
[78][79]






 O and silver sulphide protocells in 1941.
O and silver sulphide protocells in 1941.








