Theoretical ecology

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Theoretical_ecology 

 

Mathematical models developed in theoretical ecology predict complex food webs are less stable than simple webs.

Life on Earth-Flow of Energy and Entropy

Theoretical ecology is the scientific discipline devoted to the study of ecological systems using theoretical methods such as simple conceptual models, mathematical models, computational simulations, and advanced data analysis. Effective models improve understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Further, the field aims to unify a diverse range of empirical observations by assuming that common, mechanistic processes generate observable phenomena across species and ecological environments. Based on biologically realistic assumptions, theoretical ecologists are able to uncover novel, non-intuitive insights about natural processes. Theoretical results are often verified by empirical and observational studies, revealing the power of theoretical methods in both predicting and understanding the noisy, diverse biological world.

The field is broad and includes foundations in applied mathematics, computer science, biology, statistical physics, genetics, chemistry, evolution, and conservation biology. Theoretical ecology aims to explain a diverse range of phenomena in the life sciences, such as population growth and dynamics, fisheries, competition, evolutionary theory, epidemiology, animal behavior and group dynamics, food webs, ecosystems, spatial ecology, and the effects of climate change.

Theoretical ecology has further benefited from the advent of fast computing power, allowing the analysis and visualization of large-scale computational simulations of ecological phenomena. Importantly, these modern tools provide quantitative predictions about the effects of human induced environmental change on a diverse variety of ecological phenomena, such as: species invasions, climate change, the effect of fishing and hunting on food network stability, and the global carbon cycle.

Modelling approaches

As in most other sciences, mathematical models form the foundation of modern ecological theory.

• Phenomenological models: distill the functional and distributional shapes from observed patterns in the data, or researchers decide on functions and distribution that are flexible enough to match the patterns they or others (field or experimental ecologists) have found in the field or through experimentation.
• Mechanistic models: model the underlying processes directly, with functions and distributions that are based on theoretical reasoning about ecological processes of interest.

Ecological models can be deterministic or stochastic.

• Deterministic models always evolve in the same way from a given starting point. They represent the average, expected behavior of a system, but lack random variation. Many system dynamics models are deterministic.
• Stochastic models allow for the direct modeling of the random perturbations that underlie real world ecological systems. Markov chain models are stochastic.

Species can be modelled in continuous or discrete time.

• Continuous time is modelled using differential equations.
• Discrete time is modelled using difference equations. These model ecological processes that can be described as occurring over discrete time steps. Matrix algebra is often used to investigate the evolution of age-structured or stage-structured populations. The Leslie matrix, for example, mathematically represents the discrete time change of an age structured population.

Models are often used to describe real ecological reproduction processes of single or multiple species. These can be modelled using stochastic branching processes. Examples are the dynamics of interacting populations (predation competition and mutualism), which, depending on the species of interest, may best be modeled over either continuous or discrete time. Other examples of such models may be found in the field of mathematical epidemiology where the dynamic relationships that are to be modeled are host–pathogen interactions.

Bifurcation diagram of the logistic map

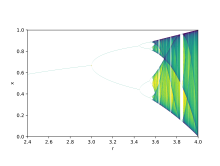
Bifurcation theory is used to illustrate how small changes in parameter values can give rise to dramatically different long run outcomes, a mathematical fact that may be used to explain drastic ecological differences that come about in qualitatively very similar systems. Logistic maps are polynomial mappings, and are often cited as providing archetypal examples of how chaotic behaviour can arise from very simple non-linear dynamical equations. The maps were popularized in a seminal 1976 paper by the theoretical ecologist Robert May. The difference equation is intended to capture the two effects of reproduction and starvation.

In 1930, R.A. Fisher published his classic The Genetical Theory of Natural Selection, which introduced the idea that frequency-dependent fitness brings a strategic aspect to evolution, where the payoffs to a particular organism, arising from the interplay of all of the relevant organisms, are the number of this organism' s viable offspring. In 1961, Richard Lewontin applied game theory to evolutionary biology in his Evolution and the Theory of Games, followed closely by John Maynard Smith, who in his seminal 1972 paper, “Game Theory and the Evolution of Fighting", defined the concept of the evolutionarily stable strategy.

Because ecological systems are typically nonlinear, they often cannot be solved analytically and in order to obtain sensible results, nonlinear, stochastic and computational techniques must be used. One class of computational models that is becoming increasingly popular are the agent-based models. These models can simulate the actions and interactions of multiple, heterogeneous, organisms where more traditional, analytical techniques are inadequate. Applied theoretical ecology yields results which are used in the real world. For example, optimal harvesting theory draws on optimization techniques developed in economics, computer science and operations research, and is widely used in fisheries.

Population ecology

Population ecology is a sub-field of ecology that deals with the dynamics of species populations and how these populations interact with the environment. It is the study of how the population sizes of species living together in groups change over time and space, and was one of the first aspects of ecology to be studied and modelled mathematically.

Exponential growth

The most basic way of modeling population dynamics is to assume that the rate of growth of a population depends only upon the population size at that time and the per capita growth rate of the organism. In other words, if the number of individuals in a population at a time t, is N(t), then the rate of population growth is given by:

${\displaystyle {\frac {dN(t)}{dt}}=rN(t)}$

where r is the per capita growth rate, or the intrinsic growth rate of the organism. It can also be described as r = b-d, where b and d are the per capita time-invariant birth and death rates, respectively. This first order linear differential equation can be solved to yield the solution

${\displaystyle N(t)=N(0)\ e^{rt}}$,

a trajectory known as Malthusian growth, after Thomas Malthus, who first described its dynamics in 1798. A population experiencing Malthusian growth follows an exponential curve, where N(0) is the initial population size. The population grows when r > 0, and declines when r < 0. The model is most applicable in cases where a few organisms have begun a colony and are rapidly growing without any limitations or restrictions impeding their growth (e.g. bacteria inoculated in rich media).

Logistic growth

The exponential growth model makes a number of assumptions, many of which often do not hold. For example, many factors affect the intrinsic growth rate and is often not time-invariant. A simple modification of the exponential growth is to assume that the intrinsic growth rate varies with population size. This is reasonable: the larger the population size, the fewer resources available, which can result in a lower birth rate and higher death rate. Hence, we can replace the time-invariant r with r’(t) = (b –a*N(t)) – (d + c*N(t)), where a and c are constants that modulate birth and death rates in a population dependent manner (e.g. intraspecific competition). Both a and c will depend on other environmental factors which, we can for now, assume to be constant in this approximated model. The differential equation is now:

${\displaystyle {\frac {dN(t)}{dt}}=((b-aN(t))-(d-cN(t)))N(t)}$

This can be rewritten as:

${\displaystyle {\frac {dN(t)}{dt}}=rN(t)\left(1-{\frac {N}{K}}\right)}$

where r = b-d and K = (b-d)/(a+c).

The biological significance of K becomes apparent when stabilities of the equilibria of the system are considered. The constant K is the carrying capacity of the population. The equilibria of the system are N = 0 and N = K. If the system is linearized, it can be seen that N = 0 is an unstable equilibrium while K is a stable equilibrium.

Structured population growth

Another assumption of the exponential growth model is that all individuals within a population are identical and have the same probabilities of surviving and of reproducing. This is not a valid assumption for species with complex life histories. The exponential growth model can be modified to account for this, by tracking the number of individuals in different age classes (e.g. one-, two-, and three-year-olds) or different stage classes (juveniles, sub-adults, and adults) separately, and allowing individuals in each group to have their own survival and reproduction rates. The general form of this model is

${\displaystyle \mathbf {N} _{t+1}=\mathbf {L} \mathbf {N} _{t}}$

where N_t is a vector of the number of individuals in each class at time t and L is a matrix that contains the survival probability and fecundity for each class. The matrix L is referred to as the Leslie matrix for age-structured models, and as the Lefkovitch matrix for stage-structured models.

If parameter values in L are estimated from demographic data on a specific population, a structured model can then be used to predict whether this population is expected to grow or decline in the long-term, and what the expected age distribution within the population will be. This has been done for a number of species including loggerhead sea turtles and right whales.

Community ecology

An ecological community is a group of trophically similar, sympatric species that actually or potentially compete in a local area for the same or similar resources. Interactions between these species form the first steps in analyzing more complex dynamics of ecosystems. These interactions shape the distribution and dynamics of species. Of these interactions, predation is one of the most widespread population activities. Taken in its most general sense, predation comprises predator–prey, host–pathogen, and host–parasitoid interactions.

Lotka–Volterra model of cheetah–baboon interactions. Starting with 80 baboons (green) and 40 cheetahs, this graph shows how the model predicts the two species numbers will progress over time.

Predator–prey interaction

Predator–prey interactions exhibit natural oscillations in the populations of both predator and the prey. In 1925, the American mathematician Alfred J. Lotka developed simple equations for predator–prey interactions in his book on biomathematics. The following year, the Italian mathematician Vito Volterra, made a statistical analysis of fish catches in the Adriatic and independently developed the same equations. It is one of the earliest and most recognised ecological models, known as the Lotka-Volterra model:

${\displaystyle {\frac {dN(t)}{dt}}=N(t)(r-\alpha P(t))}$

${\displaystyle {\frac {dP(t)}{dt}}=P(t)(c\alpha N(t)-d)}$

where N is the prey and P is the predator population sizes, r is the rate for prey growth, taken to be exponential in the absence of any predators, α is the prey mortality rate for per-capita predation (also called ‘attack rate’), c is the efficiency of conversion from prey to predator, and d is the exponential death rate for predators in the absence of any prey.

Volterra originally used the model to explain fluctuations in fish and shark populations after fishing was curtailed during the First World War. However, the equations have subsequently been applied more generally. Other examples of these models include the Lotka-Volterra model of the snowshoe hare and Canadian lynx in North America, any infectious disease modeling such as the recent outbreak of SARS  and biological control of California red scale by the introduction of its parasitoid, Aphytis melinus .

A credible, simple alternative to the Lotka-Volterra predator–prey model and their common prey dependent generalizations is the ratio dependent or Arditi-Ginzburg model. The two are the extremes of the spectrum of predator interference models. According to the authors of the alternative view, the data show that true interactions in nature are so far from the Lotka–Volterra extreme on the interference spectrum that the model can simply be discounted as wrong. They are much closer to the ratio-dependent extreme, so if a simple model is needed one can use the Arditi–Ginzburg model as the first approximation.

Host–pathogen interaction

The second interaction, that of host and pathogen, differs from predator–prey interactions in that pathogens are much smaller, have much faster generation times, and require a host to reproduce. Therefore, only the host population is tracked in host–pathogen models. Compartmental models that categorize host population into groups such as susceptible, infected, and recovered (SIR) are commonly used.

Host–parasitoid interaction

The third interaction, that of host and parasitoid, can be analyzed by the Nicholson–Bailey model, which differs from Lotka-Volterra and SIR models in that it is discrete in time. This model, like that of Lotka-Volterra, tracks both populations explicitly. Typically, in its general form, it states:

${\displaystyle N_{t+1}=\lambda \ N_{t}\ [1-f(N_{t},P_{t})]}$

${\displaystyle P_{t+1}=c\ N_{t}\ f(N_{t},p_{t})}$

where f(N_t, P_t) describes the probability of infection (typically, Poisson distribution), λ is the per-capita growth rate of hosts in the absence of parasitoids, and c is the conversion efficiency, as in the Lotka-Volterra model.

Competition and mutualism

In studies of the populations of two species, the Lotka-Volterra system of equations has been extensively used to describe dynamics of behavior between two species, N₁ and N₂. Examples include relations between D. discoiderum and E. coli, as well as theoretical analysis of the behavior of the system.

${\displaystyle {\frac {dN_{1}}{dt}}={\frac {r_{1}N_{1}}{K_{1}}}\left(K_{1}-N_{1}+\alpha _{12}N_{2}\right)}$

${\displaystyle {\frac {dN_{2}}{dt}}={\frac {r_{2}N_{2}}{K_{2}}}\left(K_{2}-N_{2}+\alpha _{21}N_{1}\right)}$

The r coefficients give a “base” growth rate to each species, while K coefficients correspond to the carrying capacity. What can really change the dynamics of a system, however are the α terms. These describe the nature of the relationship between the two species. When α₁₂ is negative, it means that N₂ has a negative effect on N₁, by competing with it, preying on it, or any number of other possibilities. When α₁₂ is positive, however, it means that N₂ has a positive effect on N₁, through some kind of mutualistic interaction between the two. When both α₁₂ and α₂₁ are negative, the relationship is described as competitive. In this case, each species detracts from the other, potentially over competition for scarce resources. When both α₁₂ and α₂₁ are positive, the relationship becomes one of mutualism. In this case, each species provides a benefit to the other, such that the presence of one aids the population growth of the other.

Neutral theory

Unified neutral theory is a hypothesis proposed by Stephen Hubbell in 2001. The hypothesis aims to explain the diversity and relative abundance of species in ecological communities, although like other neutral theories in ecology, Hubbell's hypothesis assumes that the differences between members of an ecological community of trophically similar species are "neutral," or irrelevant to their success. Neutrality means that at a given trophic level in a food web, species are equivalent in birth rates, death rates, dispersal rates and speciation rates, when measured on a per-capita basis. This implies that biodiversity arises at random, as each species follows a random walk. This can be considered a null hypothesis to niche theory. The hypothesis has sparked controversy, and some authors consider it a more complex version of other null models that fit the data better.

Under unified neutral theory, complex ecological interactions are permitted among individuals of an ecological community (such as competition and cooperation), providing all individuals obey the same rules. Asymmetric phenomena such as parasitism and predation are ruled out by the terms of reference; but cooperative strategies such as swarming, and negative interaction such as competing for limited food or light are allowed, so long as all individuals behave the same way. The theory makes predictions that have implications for the management of biodiversity, especially the management of rare species. It predicts the existence of a fundamental biodiversity constant, conventionally written θ, that appears to govern species richness on a wide variety of spatial and temporal scales.

Hubbell built on earlier neutral concepts, including MacArthur & Wilson's theory of island biogeography and Gould's concepts of symmetry and null models.

Spatial ecology

Biogeography

Biogeography is the study of the distribution of species in space and time. It aims to reveal where organisms live, at what abundance, and why they are (or are not) found in a certain geographical area.

Biogeography is most keenly observed on islands, which has led to the development of the subdiscipline of island biogeography. These habitats are often a more manageable areas of study because they are more condensed than larger ecosystems on the mainland. In 1967, Robert MacArthur and E.O. Wilson published The Theory of Island Biogeography. This showed that the species richness in an area could be predicted in terms of factors such as habitat area, immigration rate and extinction rate. The theory is considered one of the fundamentals of ecological theory. The application of island biogeography theory to habitat fragments spurred the development of the fields of conservation biology and landscape ecology.

r/K-selection theory

A population ecology concept is r/K selection theory, one of the first predictive models in ecology used to explain life-history evolution. The premise behind the r/K selection model is that natural selection pressures change according to population density. For example, when an island is first colonized, density of individuals is low. The initial increase in population size is not limited by competition, leaving an abundance of available resources for rapid population growth. These early phases of population growth experience density-independent forces of natural selection, which is called r-selection. As the population becomes more crowded, it approaches the island's carrying capacity, thus forcing individuals to compete more heavily for fewer available resources. Under crowded conditions, the population experiences density-dependent forces of natural selection, called K-selection.

The diversity and containment of coral reef systems make them good sites for testing niche and neutral theories.

Metapopulations

Spatial analysis of ecological systems often reveals that assumptions that are valid for spatially homogenous populations – and indeed, intuitive – may no longer be valid when migratory subpopulations moving from one patch to another are considered. In a simple one-species formulation, a subpopulation may occupy a patch, move from one patch to another empty patch, or die out leaving an empty patch behind. In such a case, the proportion of occupied patches may be represented as

${\displaystyle {\frac {dp}{dt}}=mp(1-p)-ep}$

where m is the rate of colonization, and e is the rate of extinction. In this model, if e < m, the steady state value of p is 1 – (e/m) while in the other case, all the patches will eventually be left empty. This model may be made more complex by addition of another species in several different ways, including but not limited to game theoretic approaches, predator–prey interactions, etc. We will consider here an extension of the previous one-species system for simplicity. Let us denote the proportion of patches occupied by the first population as p₁, and that by the second as p₂. Then,

${\displaystyle {\frac {dp_{1}}{dt}}=m_{1}p_{1}(1-p_{1})-ep_{1}}$

${\displaystyle {\frac {dp_{2}}{dt}}=m_{2}p_{2}(1-p_{1}-p_{2})-ep_{2}-mp_{1}p_{2}}$

In this case, if e is too high, p₁ and p₂ will be zero at steady state. However, when the rate of extinction is moderate, p₁ and p₂ can stably coexist. The steady state value of p₂ is given by

${\displaystyle p_{2}^{*}={\frac {e}{m_{1}}}-{\frac {m_{1}}{m_{2}}}}$

(p*₁ may be inferred by symmetry). If e is zero, the dynamics of the system favor the species that is better at colonizing (i.e. has the higher m value). This leads to a very important result in theoretical ecology known as the Intermediate Disturbance Hypothesis, where the biodiversity (the number of species that coexist in the population) is maximized when the disturbance (of which e is a proxy here) is not too high or too low, but at intermediate levels.

The form of the differential equations used in this simplistic modelling approach can be modified. For example:

1. Colonization may be dependent on p linearly (m*(1-p)) as opposed to the non-linear m*p*(1-p) regime described above. This mode of replication of a species is called the “rain of propagules”, where there is an abundance of new individuals entering the population at every generation. In such a scenario, the steady state where the population is zero is usually unstable.
2. Extinction may depend non-linearly on p (e*p*(1-p)) as opposed to the linear (e*p) regime described above. This is referred to as the “rescue effect” and it is again harder to drive a population extinct under this regime.

The model can also be extended to combinations of the four possible linear or non-linear dependencies of colonization and extinction on p are described in more detail in.

Ecosystem ecology

Introducing new elements, whether biotic or abiotic, into ecosystems can be disruptive. In some cases, it leads to ecological collapse, trophic cascades and the death of many species within the ecosystem. The abstract notion of ecological health attempts to measure the robustness and recovery capacity for an ecosystem; i.e. how far the ecosystem is away from its steady state. Often, however, ecosystems rebound from a disruptive agent. The difference between collapse or rebound depends on the toxicity of the introduced element and the resiliency of the original ecosystem.

If ecosystems are governed primarily by stochastic processes, through which its subsequent state would be determined by both predictable and random actions, they may be more resilient to sudden change than each species individually. In the absence of a balance of nature, the species composition of ecosystems would undergo shifts that would depend on the nature of the change, but entire ecological collapse would probably be infrequent events. In 1997, Robert Ulanowicz used information theory tools to describe the structure of ecosystems, emphasizing mutual information (correlations) in studied systems. Drawing on this methodology and prior observations of complex ecosystems, Ulanowicz depicts approaches to determining the stress levels on ecosystems and predicting system reactions to defined types of alteration in their settings (such as increased or reduced energy flow, and eutrophication.

Ecopath is a free ecosystem modelling software suite, initially developed by NOAA, and widely used in fisheries management as a tool for modelling and visualising the complex relationships that exist in real world marine ecosystems.

Food webs

Food webs provide a framework within which a complex network of predator–prey interactions can be organised. A food web model is a network of food chains. Each food chain starts with a primary producer or autotroph, an organism, such as a plant, which is able to manufacture its own food. Next in the chain is an organism that feeds on the primary producer, and the chain continues in this way as a string of successive predators. The organisms in each chain are grouped into trophic levels, based on how many links they are removed from the primary producers. The length of the chain, or trophic level, is a measure of the number of species encountered as energy or nutrients move from plants to top predators. Food energy flows from one organism to the next and to the next and so on, with some energy being lost at each level. At a given trophic level there may be one species or a group of species with the same predators and prey.

In 1927, Charles Elton published an influential synthesis on the use of food webs, which resulted in them becoming a central concept in ecology. In 1966, interest in food webs increased after Robert Paine's experimental and descriptive study of intertidal shores, suggesting that food web complexity was key to maintaining species diversity and ecological stability. Many theoretical ecologists, including Sir Robert May and Stuart Pimm, were prompted by this discovery and others to examine the mathematical properties of food webs. According to their analyses, complex food webs should be less stable than simple food webs. The apparent paradox between the complexity of food webs observed in nature and the mathematical fragility of food web models is currently an area of intensive study and debate. The paradox may be due partially to conceptual differences between persistence of a food web and equilibrial stability of a food web.

Systems ecology

Systems ecology can be seen as an application of general systems theory to ecology. It takes a holistic and interdisciplinary approach to the study of ecological systems, and particularly ecosystems. Systems ecology is especially concerned with the way the functioning of ecosystems can be influenced by human interventions. Like other fields in theoretical ecology, it uses and extends concepts from thermodynamics and develops other macroscopic descriptions of complex systems. It also takes account of the energy flows through the different trophic levels in the ecological networks. Systems ecology also considers the external influence of ecological economics, which usually is not otherwise considered in ecosystem ecology. For the most part, systems ecology is a subfield of ecosystem ecology.

Ecophysiology

This is the study of how "the environment, both physical and biological, interacts with the physiology of an organism. It includes the effects of climate and nutrients on physiological processes in both plants and animals, and has a particular focus on how physiological processes scale with organism size".

Behavioral ecology

Swarm behaviour

Flocks of birds can abruptly change their direction in unison, and then, just as suddenly, make a unanimous group decision to land.

Swarm behaviour is a collective behaviour exhibited by animals of similar size which aggregate together, perhaps milling about the same spot or perhaps migrating in some direction. Swarm behaviour is commonly exhibited by insects, but it also occurs in the flocking of birds, the schooling of fish and the herd behaviour of quadrupeds. It is a complex emergent behaviour that occurs when individual agents follow simple behavioral rules.

Recently, a number of mathematical models have been discovered which explain many aspects of the emergent behaviour. Swarm algorithms follow a Lagrangian approach or an Eulerian approach. The Eulerian approach views the swarm as a field, working with the density of the swarm and deriving mean field properties. It is a hydrodynamic approach, and can be useful for modelling the overall dynamics of large swarms. However, most models work with the Lagrangian approach, which is an agent-based model following the individual agents (points or particles) that make up the swarm. Individual particle models can follow information on heading and spacing that is lost in the Eulerian approach. Examples include ant colony optimization, self-propelled particles and particle swarm optimization

Evolutionary ecology

The British biologist Alfred Russel Wallace is best known for independently proposing a theory of evolution due to natural selection that prompted Charles Darwin to publish his own theory. In his famous 1858 paper, Wallace proposed natural selection as a kind of feedback mechanism which keeps species and varieties adapted to their environment.

The action of this principle is exactly like that of the centrifugal governor of the steam engine, which checks and corrects any irregularities almost before they become evident; and in like manner no unbalanced deficiency in the animal kingdom can ever reach any conspicuous magnitude, because it would make itself felt at the very first step, by rendering existence difficult and extinction almost sure soon to follow.

The cybernetician and anthropologist Gregory Bateson observed in the 1970s that, though writing it only as an example, Wallace had "probably said the most powerful thing that’d been said in the 19th Century". Subsequently, the connection between natural selection and systems theory has become an area of active research.

Other theories

In contrast to previous ecological theories which considered floods to be catastrophic events, the river flood pulse concept argues that the annual flood pulse is the most important aspect and the most biologically productive feature of a river's ecosystem.

History

Theoretical ecology draws on pioneering work done by G. Evelyn Hutchinson and his students. Brothers H.T. Odum and E.P. Odum are generally recognised as the founders of modern theoretical ecology. Robert MacArthur brought theory to community ecology. Daniel Simberloff was the student of E.O. Wilson, with whom MacArthur collaborated on The Theory of Island Biogeography, a seminal work in the development of theoretical ecology.

Simberloff added statistical rigour to experimental ecology and was a key figure in the SLOSS debate, about whether it is preferable to protect a single large or several small reserves. This resulted in the supporters of Jared Diamond's community assembly rules defending their ideas through Neutral Model Analysis. Simberloff also played a key role in the (still ongoing) debate on the utility of corridors for connecting isolated reserves.

Stephen Hubbell and Michael Rosenzweig combined theoretical and practical elements into works that extended MacArthur and Wilson's Island Biogeography Theory - Hubbell with his Unified Neutral Theory of Biodiversity and Biogeography and Rosenzweig with his Species Diversity in Space and Time.

Theoretical and mathematical ecologists

A tentative distinction can be made between mathematical ecologists, ecologists who apply mathematics to ecological problems, and mathematicians who develop the mathematics itself that arises out of ecological problems.

Some notable theoretical ecologists can be found in these categories:

• Category:Mathematical ecologists
• Category:Theoretical biologists

Journals

• The American Naturalist
• Journal of Mathematical Biology
• Journal of Theoretical Biology
• Theoretical Ecology
• Theoretical Population Biology
• Ecological Modelling

Systems theory

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Systems_theory 

 

Systems theory is the interdisciplinary study of systems, which are cohesive groups of interrelated, interdependent parts that can be natural or human-made. Every system is bounded by space and time, influenced by its environment, defined by its structure and purpose, and expressed through its functioning. A system may be more than the sum of its parts if it expresses synergy or emergent behavior.

Changing one part of a system may affect other parts or the whole system. It may be possible to predict these changes in patterns of behavior. For systems that learn and adapt, the growth and the degree of adaptation depend upon how well the system is engaged with its environment. Some systems support other systems, maintaining the other system to prevent failure. The goals of systems theory are to model a system's dynamics, constraints, conditions, and to elucidate principles (such as purpose, measure, methods, tools) that can be discerned and applied to other systems at every level of nesting, and in a wide range of fields for achieving optimized equifinality.

General systems theory is about developing broadly applicable concepts and principles, as opposed to concepts and principles specific to one domain of knowledge. It distinguishes dynamic or active systems from static or passive systems. Active systems are activity structures or components that interact in behaviours and processes. Passive systems are structures and components that are being processed. For example, a program is passive when it is a disc file and active when it runs in memory. The field is related to systems thinking, machine logic, and systems engineering.

Key concepts

• System: a group of interacting, interdependent parts that form a complex whole.
• Boundaries: barriers that define a system and distinguish it from other systems in an environment.
• Homeostasis: the tendency of a system to be resilient with respect to external disruption and to maintain its key characteristics.
• Adaptation: the tendency of a system to make the internal changes to protect itself and keep fulfilling its purpose.
• Reciprocal transactions: circular or cyclical interactions that systems engage in such that they influence one another.
• Feedback loop: the process by which systems self-correct based on reactions from other systems in the environment.
• Throughput: the rate of energy transfer between a system and its environment over time.
• Microsystem: the system closest to the client.
• Mesosystem: relationships among systems in an environment.
• Exosystem: a relationship between two systems that has an indirect effect on a third system.
• Macrosystem: a larger system that influences clients, such as policies, administration of entitlement programs, and culture.
• Equifinality: the way systems can reach the same goal through different paths.
• Open and closed systems
• Chronosystem: a system composed of significant life events affecting adaptation.
• Isomorphism: structural, behavioral, and developmental features that are shared across systems.
• Systems architecture:
• Systems analysis:

Systems thinking

Systems thinking is the ability or skill to perform problem solving in complex systems. In application it has been defined as both a skill and an awareness. A system is an entity with interrelated and interdependent parts; it is defined by its boundaries and is more than the sum of its parts (subsystem). Changing one part of the system affects other parts and the whole system, with predictable patterns of behavior. Furthermore, the individuals working as part of a system are components as well, therefore contributing to its outcome.

Overview

Systems theory is manifest in the work of practitioners in many disciplines, for example the works of biologist Ludwig von Bertalanffy, linguist Béla H. Bánáthy, and sociologist Talcott Parsons; in the study of ecological systems by Howard T. Odum, Eugene Odum; in Fritjof Capra's study of organizational theory; in the study of management by Peter Senge; in interdisciplinary areas such as Human Resource Development in the works of Richard A. Swanson; and in the works of educators Debora Hammond and Alfonso Montuori.

As a transdisciplinary, interdisciplinary, and multiperspectival endeavor, systems theory brings together principles and concepts from ontology, the philosophy of science, physics, computer science, biology, and engineering, as well as geography, sociology, political science, psychotherapy (especially family systems therapy), and economics.

Systems theory promotes dialogue between autonomous areas of study as well as within systems science itself. In this respect, with the possibility of misinterpretations, von Bertalanffy believed a general theory of systems "should be an important regulative device in science," to guard against superficial analogies that "are useless in science and harmful in their practical consequences."

Others remain closer to the direct systems concepts developed by the original systems theorists. For example, Ilya Prigogine, of the Center for Complex Quantum Systems at the University of Texas, has studied emergent properties, suggesting that they offer analogues for living systems. The distinction of autopoiesis as made by Humberto Maturana and Francisco Varela represent further developments in this field. Important names in contemporary systems science include Russell Ackoff, Ruzena Bajcsy, Béla H. Bánáthy, Gregory Bateson, Anthony Stafford Beer, Peter Checkland, Barbara Grosz, Brian Wilson, Robert L. Flood, Allenna Leonard, Radhika Nagpal, Fritjof Capra, Warren McCulloch, Kathleen Carley, Michael C. Jackson, Katia Sycara, and Edgar Morin among others.

With the modern foundations for a general theory of systems following World War I, Ervin László, in the preface for Bertalanffy's book, Perspectives on General System Theory, points out that the translation of "general system theory" from German into English has "wrought a certain amount of havoc":

It (General System Theory) was criticized as pseudoscience and said to be nothing more than an admonishment to attend to things in a holistic way. Such criticisms would have lost their point had it been recognized that von Bertalanffy's general system theory is a perspective or paradigm, and that such basic conceptual frameworks play a key role in the development of exact scientific theory. .. Allgemeine Systemtheorie is not directly consistent with an interpretation often put on 'general system theory,' to wit, that it is a (scientific) "theory of general systems." To criticize it as such is to shoot at straw men. Von Bertalanffy opened up something much broader and of much greater significance than a single theory (which, as we now know, can always be falsified and has usually an ephemeral existence): he created a new paradigm for the development of theories.

Theorie (or Lehre) "has a much broader meaning in German than the closest English words 'theory' and 'science'," just as Wissenschaft (or 'Science'). These ideas refer to an organized body of knowledge and "any systematically presented set of concepts, whether empirically, axiomatically, or philosophically" represented, while many associate Lehre with theory and science in the etymology of general systems, though it also does not translate from the German very well; its "closest equivalent" translates to 'teaching', but "sounds dogmatic and off the mark." While the idea of a "general systems theory" might have lost many of its root meanings in the translation, by defining a new way of thinking about science and scientific paradigms, systems theory became a widespread term used for instance to describe the interdependence of relationships created in organizations.

A system in this frame of reference can contain regularly interacting or interrelating groups of activities. For example, in noting the influence in the evolution of "an individually oriented industrial psychology [into] a systems and developmentally oriented organizational psychology," some theorists recognize that organizations have complex social systems; separating the parts from the whole reduces the overall effectiveness of organizations. This difference, from conventional models that center on individuals, structures, departments and units, separates in part from the whole, instead of recognizing the interdependence between groups of individuals, structures and processes that enable an organization to function.

László explains that the new systems view of organized complexity went "one step beyond the Newtonian view of organized simplicity" which reduced the parts from the whole, or understood the whole without relation to the parts. The relationship between organisations and their environments can be seen as the foremost source of complexity and interdependence. In most cases, the whole has properties that cannot be known from analysis of the constituent elements in isolation.

Béla H. Bánáthy, who argued—along with the founders of the systems society—that "the benefit of humankind" is the purpose of science, has made significant and far-reaching contributions to the area of systems theory. For the Primer Group at the International Society for the System Sciences, Bánáthy defines a perspective that iterates this view:

The systems view is a world-view that is based on the discipline of SYSTEM INQUIRY. Central to systems inquiry is the concept of SYSTEM. In the most general sense, system means a configuration of parts connected and joined together by a web of relationships. The Primer Group defines system as a family of relationships among the members acting as a whole. Von Bertalanffy defined system as "elements in standing relationship."

Examples of applications

Marketing operations

Key concepts Benchmarking Best practices Budgeting Business intelligence Business process Change management Chief Marketing Officer (CMO) Customer intelligence Customer lifecycle management Customer lifetime value Data quality Data warehouses Database marketing Demand generation Digital asset management Flowchart Infrastructure Lead generation Marketing accountability Marketing automation Marketing effectiveness Organization development Post-merger integration Predictive analytics Predictive modelling Process optimization Return on marketing investment Strategic planning Systems theory

In biology

Systems biology is a movement that draws on several trends in bioscience research. Proponents describe systems biology as a biology-based interdisciplinary study field that focuses on complex interactions in biological systems, claiming that it uses a new perspective (holism instead of reduction).

Particularly from the year 2000 onwards, the biosciences use the term widely and in a variety of contexts. An often stated ambition of systems biology is the modelling and discovery of emergent properties which represents properties of a system whose theoretical description requires the only possible useful techniques to fall under the remit of systems biology. It is thought that Ludwig von Bertalanffy may have created the term systems biology in 1928.

Subdisciplines of systems biology include:

• Systems neuroscience
• Systems pharmacology

Ecology

Systems ecology is an interdisciplinary field of ecology that takes a holistic approach to the study of ecological systems, especially ecosystems; it can be seen as an application of general systems theory to ecology.

Central to the systems ecology approach is the idea that an ecosystem is a complex system exhibiting emergent properties. Systems ecology focuses on interactions and transactions within and between biological and ecological systems, and is especially concerned with the way the functioning of ecosystems can be influenced by human interventions. It uses and extends concepts from thermodynamics and develops other macroscopic descriptions of complex systems.

In chemistry

Systems chemistry is the science of studying networks of interacting molecules, to create new functions from a set (or library) of molecules with different hierarchical levels and emergent properties. Systems chemistry is also related to the origin of life (abiogenesis).

In engineering

Systems engineering is an interdisciplinary approach and means for enabling the realisation and deployment of successful systems. It can be viewed as the application of engineering techniques to the engineering of systems, as well as the application of a systems approach to engineering efforts. Systems engineering integrates other disciplines and specialty groups into a team effort, forming a structured development process that proceeds from concept to production to operation and disposal. Systems engineering considers both the business and the technical needs of all customers, with the goal of providing a quality product that meets the user's needs.

User-centered design process

Systems thinking is a crucial part of user-centered design processes and is necessary to understand the whole impact of a new human computer interaction (HCI) Information System. Overlooking this and developing software without insights input from the future users (mediated by user experience designers) is a serious design flaw that can lead to complete failure of information systems, increased stress and mental illness for users of information systems leading to increased costs and a huge waste of resources. It is currently surprisingly uncommon for organizations and governments to investigate the project management decisions leading to serious design flaws and lack of usability.

The Institute of Electrical and Electronics Engineers estimates that roughly 15% of the estimated $1 trillion used to develop information systems every year is completely wasted and the produced systems are discarded before implementation by entirely preventable mistakes. According to the CHAOS report published in 2018 by the Standish Group, a vast majority of information systems fail or partly fail according to their survey:

Pure success is the combination of high customer satisfaction with high return on value to the organization. Related figures for the year 2017 are: successful: 14%, challenged: 67%, failed 19%.

In mathematics

System dynamics is an approach to understanding the nonlinear behaviour of complex systems over time using stocks, flows, internal feedback loops, and time delays.

In social sciences and humanities

• Systems theory in anthropology
• Systems theory in archaeology
• Systems theory in political science

Psychology

Systems psychology is a branch of psychology that studies human behaviour and experience in complex systems.

It received inspiration from systems theory and systems thinking, as well as the basics of theoretical work from Roger Barker, Gregory Bateson, Humberto Maturana and others. It makes an approach in psychology in which groups and individuals receive consideration as systems in homeostasis. Systems psychology "includes the domain of engineering psychology, but in addition seems more concerned with societal systems and with the study of motivational, affective, cognitive and group behavior that holds the name engineering psychology."

In systems psychology, characteristics of organizational behaviour (such as individual needs, rewards, expectations, and attributes of the people interacting with the systems) "considers this process in order to create an effective system."

History

Timeline

Predecessors Saint-Simon (1760–1825), Karl Marx (1817–83), Friedrich Engels (1820–95), Herbert Spencer (1820–1903), Rudolf Clausius (1822–88), Vilfredo Pareto (1848–1923), Émile Durkheim (1858–1917), Alexander Bogdanov (1873–1928), Nicolai Hartmann (1882–1950), Robert Maynard Hutchins (1929–51), among others Founders 1946–53: Macy conferences 1948: Norbert Wiener publishes Cybernetics: Or Control and Communication in the Animal and the Machine 1951: Talcott Parsons publishes The Social System[29] 1954: The Society for the Advancement of General Systems Theory is established by Ludwig von Bertalanffy, Anatol Rapoport, Ralph W. Gerard, Kenneth Boulding. 1955: W. Ross Ashby publishes Introduction to Cybernetics 1968: Bertalanffy publishes General System Theory: Foundations, Development, Applications Other contributors 1970–80s Second-order cybernetics (Heinz von Foerster, Gregory Bateson, Humberto Maturana, and others) 1971–73 Cybersyn, rudimentary internet and cybernetic system for democratic economic planning developed by Stafford Beer in Chile under the Allende government 1970s: Catastrophe theory (René Thom, E.C. Zeeman) Dynamical systems in mathematics. 1977: Ilya Prigogine received the Nobel Prize for his works on self-organization, conciliating important systems theory concepts with system thermodynamics. 1980s: Chaos theory (David Ruelle, Edward Lorenz, Mitchell Feigenbaum, Steve Smale, James A. Yorke) 1986: Context theory (Anthony Wilden) 1988: International Society for Systems Science is established. 1990: Complex adaptive systems (John H. Holland, Murray Gell-Mann, W. Brian Arthur)

Precursors

Systems thinking can date back to antiquity, whether considering the first systems of written communication with Sumerian cuneiform to Mayan numerals, or the feats of engineering with the Egyptian pyramids. Differentiated from Western rationalist traditions of philosophy, C. West Churchman often identified with the I Ching as a systems approach sharing a frame of reference similar to pre-Socratic philosophy and Heraclitus. Ludwig von Bertalanffy traced systems concepts to the philosophy of G.W. Leibniz and Nicholas of Cusa's coincidentia oppositorum. While modern systems can seem considerably more complicated, they may embed themselves in history.

Figures like James Joule and Sadi Carnot represent an important step to introduce the systems approach into the (rationalist) hard sciences of the 19th century, also known as the energy transformation. Then, the thermodynamics of this century, by Rudolf Clausius, Josiah Gibbs and others, established the system reference model as a formal scientific object.

Similar ideas are found in learning theories that developed from the same fundamental concepts, emphasising how understanding results from knowing concepts both in part and as a whole. In fact, Bertalanffy's organismic psychology paralleled the learning theory of Jean Piaget. Some consider interdisciplinary perspectives critical in breaking away from industrial age models and thinking, wherein history represents history and math represents math, while the arts and sciences specialization remain separate and many treat teaching as behaviorist conditioning.

The contemporary work of Peter Senge provides detailed discussion of the commonplace critique of educational systems grounded in conventional assumptions about learning, including the problems with fragmented knowledge and lack of holistic learning from the "machine-age thinking" that became a "model of school separated from daily life." In this way, some systems theorists attempt to provide alternatives to, and evolved ideation from orthodox theories which have grounds in classical assumptions, including individuals such as Max Weber and Émile Durkheim in sociology and Frederick Winslow Taylor in scientific management. The theorists sought holistic methods by developing systems concepts that could integrate with different areas.

Some may view the contradiction of reductionism in conventional theory (which has as its subject a single part) as simply an example of changing assumptions. The emphasis with systems theory shifts from parts to the organization of parts, recognizing interactions of the parts as not static and constant but dynamic processes. Some questioned the conventional closed systems with the development of open systems perspectives. The shift originated from absolute and universal authoritative principles and knowledge to relative and general conceptual and perceptual knowledge and still remains in the tradition of theorists that sought to provide means to organize human life. In other words, theorists rethought the preceding history of ideas; they did not lose them. Mechanistic thinking was particularly critiqued, especially the industrial-age mechanistic metaphor for the mind from interpretations of Newtonian mechanics by Enlightenment philosophers and later psychologists that laid the foundations of modern organizational theory and management by the late 19th century.

Founding and early development

Where assumptions in Western science from Plato and Aristotle to Isaac Newton's Principia (1687) have historically influenced all areas from the hard to social sciences (see, David Easton's seminal development of the "political system" as an analytical construct), the original systems theorists explored the implications of 20th-century advances in terms of systems.

Between 1929 to 1951, Robert Maynard Hutchins at the University of Chicago had undertaken efforts to encourage innovation and interdisciplinary research in the social sciences, aided by the Ford Foundation with the University's interdisciplinary Division of the Social Sciences established in 1931.

Many early systems theorists aimed at finding a general systems theory that could explain all systems in all fields of science.

"General systems theory" (GST; German: allgemeine Systemlehre) was coined in the 1940s by Ludwig von Bertalanffy, who initially sought to find a new approach to the study of living systems. Bertalanffy first developed the theory via lectures beginning in 1937 and then via publications beginning in 1946. According to Mike C. Jackson (2000), Bertalanffy promoted an embryonic form of GST as early as the 1920s and 1930s, but it was not until the early 1950s that it became more widely known in scientific circles.

Jackson also claimed that Bertalanffy's work was informed by Alexander Bogdanov's three-volume Tectology (1912-1917), providing the conceptual base for GST. A similar position is held by Richard Mattessich (1978) and Capra (1996). Despite this, Bertalanffy never even mentioned Bogdanov in his works.

The systems view was based on several fundamental ideas. First, all phenomena can be viewed as a web of relationships among elements, or a system. Second, all systems, whether electrical, biological, or social, have common patterns, behaviors, and properties that the observer can analyze and use to develop greater insight into the behavior of complex phenomena and to move closer toward a unity of the sciences. System philosophy, methodology and application are complementary to this science.

Cognizant of advances in science that questioned classical assumptions in the organizational sciences, Bertalanffy's idea to develop a theory of systems began as early as the interwar period, publishing "An Outline for General Systems Theory" in the British Journal for the Philosophy of Science by 1950.

In 1954, von Bertalanffy, along with Anatol Rapoport, Ralph W. Gerard, and Kenneth Boulding, came together at the Center for Advanced Study in the Behavioral Sciences in Palo Alto to discuss the creation of a "society for the advancement of General Systems Theory." In December that year, a meeting of around 70 people was held in Berkeley to form a society for the exploration and development of GST. The Society for General Systems Research (renamed the International Society for Systems Science in 1988) was established in 1956 thereafter as an affiliate of the American Association for the Advancement of Science (AAAS), specifically catalyzing systems theory as an area of study. The field developed from the work of Bertalanffy, Rapoport, Gerard, and Boulding, as well as other theorists in the 1950s like William Ross Ashby, Margaret Mead, Gregory Bateson, and C. West Churchman, among others.

Bertalanffy's ideas were adopted by others, working in mathematics, psychology, biology, game theory, and social network analysis. Subjects that were studied included those of complexity, self-organization, connectionism and adaptive systems. In fields like cybernetics, researchers such as Ashby, Norbert Wiener, John von Neumann, and Heinz von Foerster examined complex systems mathematically; Von Neumann discovered cellular automata and self-reproducing systems, again with only pencil and paper. Aleksandr Lyapunov and Jules Henri Poincaré worked on the foundations of chaos theory without any computer at all. At the same time, Howard T. Odum, known as a radiation ecologist, recognized that the study of general systems required a language that could depict energetics, thermodynamics and kinetics at any system scale. To fulfill this role, Odum developed a general system, or universal language, based on the circuit language of electronics, known as the Energy Systems Language.

The Cold War affected the research project for systems theory in ways that sorely disappointed many of the seminal theorists. Some began to recognize that theories defined in association with systems theory had deviated from the initial general systems theory view. Economist Kenneth Boulding, an early researcher in systems theory, had concerns over the manipulation of systems concepts. Boulding concluded from the effects of the Cold War that abuses of power always prove consequential and that systems theory might address such issues. Since the end of the Cold War, a renewed interest in systems theory emerged, combined with efforts to strengthen an ethical view on the subject.

In sociology, systems thinking also began in the 20th century, including Talcott Parsons' action  and Niklas Luhmann's social systems theory. According to Rudolf Stichweh (2011):

Since its beginnings the social sciences were an important part of the establishment of systems theory... [T]he two most influential suggestions were the comprehensive sociological versions of systems theory which were proposed by Talcott Parsons since the 1950s and by Niklas Luhmann since the 1970s.

Elements of systems thinking can also be seen in the work of James Clerk Maxwell, particularly control theory.

General systems research and systems inquiry

Many early systems theorists aimed at finding a general systems theory that could explain all systems in all fields of science. Ludwig von Bertalanffy began developing his 'general systems theory' via lectures in 1937 and then via publications from 1946. The concept was given extensive focus in his 1968 book, General System Theory: Foundations, Development, Applications.

Bertalanffy's objective was to bring together under one heading the organismic science that he had observed in his work as a biologist. His desire was to use the word system for those principles that are common to systems in general. In General System Theory (1968), he wrote:

[T]here exist models, principles, and laws that apply to generalized systems or their subclasses, irrespective of their particular kind, the nature of their component elements, and the relationships or "forces" between them. It seems legitimate to ask for a theory, not of systems of a more or less special kind, but of universal principles applying to systems in general.

In the preface to von Bertalanffy's Perspectives on General System Theory, Ervin László stated:

Thus when von Bertalanffy spoke of Allgemeine Systemtheorie it was consistent with his view that he was proposing a new perspective, a new way of doing science. It was not directly consistent with an interpretation often put on "general system theory", to wit, that it is a (scientific) "theory of general systems." To criticize it as such is to shoot at straw men. Von Bertalanffy opened up something much broader and of much greater significance than a single theory (which, as we now know, can always be falsified and has usually an ephemeral existence): he created a new paradigm for the development of theories.

Bertalanffy outlines systems inquiry into three major domains: Philosophy, Science, and Technology. In his work with the Primer Group, Béla H. Bánáthy generalized the domains into four integratable domains of systemic inquiry.

1. Philosophy: the ontology, epistemology, and axiology of systems
2. Theory: a set of interrelated concepts and principles applying to all systems/
3. Methodology: the set of models, strategies, methods and tools that instrumentalize systems theory and philosophy
4. Application: the application and interaction of the domains

These operate in a recursive relationship, he explained; integrating 'philosophy' and 'theory' as knowledge, and 'method' and 'application' as action, systems inquiry is thus knowledgeable action.

System types and fields

Theoretical fields

• Chaos theory
• Complex system
• Control theory
• Dynamical systems theory
• Earth system science
• Ecological systems theory
• Living systems theory
• Sociotechnical system
• Systemics
• Urban metabolism
• World-systems theory

Cybernetics

Cybernetics is the study of the communication and control of regulatory feedback both in living and lifeless systems (organisms, organizations, machines), and in combinations of those. Its focus is how anything (digital, mechanical or biological) controls its behavior, processes information, reacts to information, and changes or can be changed to better accomplish those three primary tasks.

The terms systems theory and cybernetics have been widely used as synonyms. Some authors use the term cybernetic systems to denote a proper subset of the class of general systems, namely those systems that include feedback loops. However, Gordon Pask's differences of eternal interacting actor loops (that produce finite products) makes general systems a proper subset of cybernetics. In cybernetics, complex systems have been examined mathematically by such researchers as W. Ross Ashby, Norbert Wiener, John von Neumann, and Heinz von Foerster.

Threads of cybernetics began in the late 1800s that led toward the publishing of seminal works (such as Wiener's Cybernetics in 1948 and Bertalanffy's General Systems Theory in 1968). Cybernetics arose more from engineering fields and GST from biology. If anything, it appears that although the two probably mutually influenced each other, cybernetics had the greater influence. Bertalanffy specifically made the point of distinguishing between the areas in noting the influence of cybernetics:

Systems theory is frequently identified with cybernetics and control theory. This again is incorrect. Cybernetics as the theory of control mechanisms in technology and nature is founded on the concepts of information and feedback, but as part of a general theory of systems.... [T]he model is of wide application but should not be identified with 'systems theory' in general ... [and] warning is necessary against its incautious expansion to fields for which its concepts are not made.

Cybernetics, catastrophe theory, chaos theory and complexity theory have the common goal to explain complex systems that consist of a large number of mutually interacting and interrelated parts in terms of those interactions. Cellular automata, neural networks, artificial intelligence, and artificial life are related fields, but do not try to describe general (universal) complex (singular) systems. The best context to compare the different "C"-Theories about complex systems is historical, which emphasizes different tools and methodologies, from pure mathematics in the beginning to pure computer science today. Since the beginning of chaos theory, when Edward Lorenz accidentally discovered a strange attractor with his computer, computers have become an indispensable source of information. One could not imagine the study of complex systems without the use of computers today.

System types

• Biological
  • Anatomical systems
    • Nervous
      • Sensory
  • Ecological systems
  • Living systems
• Complex
  • Complex adaptive system
• Conceptual
  • Coordinate
  • Deterministic (philosophy)
  • Digital ecosystem
  • Experimental
  • Writing
• Coupled human–environment
• Database
• Deterministic (science)
• Mathematical
  • Dynamical system
  • Formal system
• Economic
• Energy
• Holarchical
• Information
• Legal
• Measurement
  • Imperial
  • Metric
• Multi-agent
• Nonlinear
• Operating
• Planetary
• Political
• Social
• Star

Complex adaptive systems

Complex adaptive systems (CAS), coined by John H. Holland, Murray Gell-Mann, and others at the interdisciplinary Santa Fe Institute, are special cases of complex systems: they are complex in that they are diverse and composed of multiple, interconnected elements; they are adaptive in that they have the capacity to change and learn from experience.

In contrast to control systems, in which negative feedback dampens and reverses disequilibria, CAS are often subject to positive feedback, which magnifies and perpetuates changes, converting local irregularities into global features.