Pion

From Wikipedia, the free encyclopedia

Pion

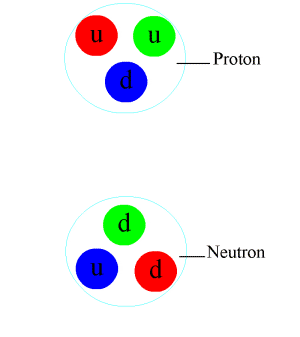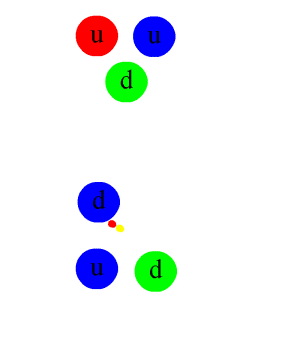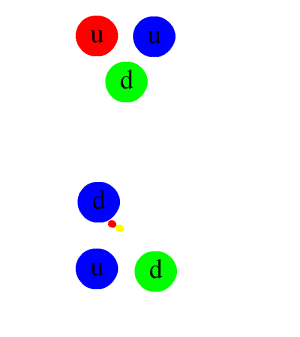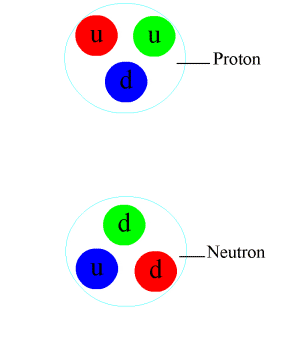
The quark structure of the pion.
Composition	π+: u d π0: u u or d d π−: d u
Statistics	Bosonic
Interactions	Strong, Weak, Electromagnetic and Gravity
Symbol	π+, π0, and π−
Theorized	Hideki Yukawa (1935)
Discovered	César Lattes, Giuseppe Occhialini (1947) and Cecil Powell
Types	3
Mass	π±: 139.57018(35) MeV/c2 π0: 134.9766(6) MeV/c2
Electric charge	π+: +1 e π0: 0 e π−: −1 e
Spin	0
Parity	−1

In particle physics, a pion (or a pi meson, denoted with the Greek letter pi:
π
) is any of three subatomic particles:
π⁰,
π⁺, and
π⁻. Each pion consists of a quark and an antiquark and is therefore a meson. Pions are the lightest mesons and, more generally, the lightest hadrons. They are unstable, with the charged pions
π⁺ and
π⁻ decaying with a mean lifetime of 26.033 nanoseconds (2.6033×10⁻⁸ seconds), and the neutral pion
π⁰ decaying with a much shorter lifetime of 8.4×10⁻¹⁷ seconds. Charged pions most often decay into muons and muon neutrinos, while neutral pions generally decay into gamma rays.

The exchange of virtual pions, along with the vector, rho and omega mesons, provides an explanation for the residual strong force between nucleons. Pions are not produced in radioactive decay, but are commonly produced in high energy accelerators in collisions between hadrons. All types of pions are also produced in natural processes when high energy cosmic ray protons and other hadronic cosmic ray components interact with matter in the Earth's atmosphere. Recently, the detection of characteristic gamma rays originating from the decay of neutral pions in two supernova remnants has shown that pions are produced copiously after supernovas, most probably in conjunction with production of high energy protons that are detected on Earth as cosmic rays.^[1]

The concept of mesons as the carrier particles of the nuclear force was first proposed in 1935 by Hideki Yukawa. While the muon was first proposed to be this particle after its discovery in 1936, later work found that it did not participate in the strong nuclear interaction. The pions, which turned out to be examples of Yukawa's proposed mesons, were discovered later: the charged pions in 1947, and the neutral pion in 1950.

History

An animation of the nuclear force (or residual strong force) interaction. The small colored double disks are gluons. Anticolors are shown as per this diagram (larger version).

 

The same process as in the animation with the individual quark constituents shown, to illustrate how the fundamental strong interaction gives rise to the nuclear force. Straight lines are quarks, while multi-colored loops are gluons (the carriers of the fundamental force). Other gluons, which bind together the proton, neutron, and pion "in-flight," are not shown.

Theoretical work by Hideki Yukawa in 1935 had predicted the existence of mesons as the carrier particles of the strong nuclear force. From the range of the strong nuclear force (inferred from the radius of the atomic nucleus), Yukawa predicted the existence of a particle having a mass of about 100 MeV. Initially after its discovery in 1936, the muon (initially called the "mu meson") was thought to be this particle, since it has a mass of 106 MeV. However, later experiments showed that the muon did not participate in the strong nuclear interaction. In modern terminology, this makes the muon a lepton, and not a meson. However, some communities of astrophysicists continue to call the muon a "mu-meson".

In 1947, the first true mesons, the charged pions, were found by the collaboration of Cecil Powell, César Lattes, Giuseppe Occhialini, et al., at the University of Bristol, in England. Since the advent of particle accelerators had not yet come, high-energy subatomic particles were only obtainable from atmospheric cosmic rays. Photographic emulsions based on the gelatin-silver process were placed for long periods of time in sites located at high altitude mountains, first at Pic du Midi de Bigorre in the Pyrenees, and later at Chacaltaya in the Andes Mountains, where the plates were struck by cosmic rays.

After the development of the photographic plates, microscopic inspection of the emulsions revealed the tracks of charged subatomic particles. Pions were first identified by their unusual "double meson" tracks, which were left by their decay into a putative meson. The particle was identified as a muon, which is not typically classified as a meson in modern particle physics. In 1948, Lattes, Eugene Gardner, and their team first artificially produced pions at the University of California's cyclotron in Berkeley, California, by bombarding carbon atoms with high-speed alpha particles. Further advanced theoretical work was carried out by Riazuddin, who in 1959, used the dispersion relation for Compton scattering of virtual photons on pions to analyze their charge radius.^[2]

Nobel Prizes in Physics were awarded to Yukawa in 1949 for his theoretical prediction of the existence of mesons, and to Cecil Powell in 1950 for developing and applying the technique of particle detection using photographic emulsions.

Since the neutral pion is not electrically charged, it is more difficult to detect and observe than the charged pions are. Neutral pions do not leave tracks in photographic emulsions or Wilson cloud chambers. The existence of the neutral pion was inferred from observing its decay products from cosmic rays, a so-called "soft component" of slow electrons with photons. The
π⁰ was identified definitively at the University of California's cyclotron in 1950 by observing its decay into two photons.^[3] Later in the same year, they were also observed in cosmic-ray balloon experiments at Bristol University.

The pion also plays a crucial role in cosmology, by imposing an upper limit on the energies of cosmic rays surviving collisions with the cosmic microwave background, through the Greisen–Zatsepin–Kuzmin limit.

In the standard understanding of the strong force interaction as defined by quantum chromodynamics, pions are loosely portrayed as Goldstone bosons of spontaneously broken chiral symmetry. That explains why the masses of the three kinds of pions are considerably less than that of the other mesons, such as the scalar or vector mesons. If their current quarks were massless particles, it could make the chiral symmetry exact and thus the Goldstone theorem would dictate that all pions have a zero mass. Empirically, since the light quarks actually have minuscule nonzero masses, the pions also have nonzero rest masses. However, those weights are almost an order of magnitude smaller than that of the nucleons, roughly^[4] m_π ≈ √v m_q / f_π ≈ √m_q 45 MeV, where m are the relevant current quark masses in MeV, 5−10 MeVs.

The use of pions in medical radiation therapy, such as for cancer, was explored at a number of research institutions, including the Los Alamos National Laboratory's Meson Physics Facility, which treated 228 patients between 1974 and 1981 in New Mexico,^[5] and the TRIUMF laboratory in Vancouver, British Columbia.

Theoretical overview

The pion can be thought of as one of the particles that mediate the interaction between a pair of nucleons. This interaction is attractive: it pulls the nucleons together. Written in a non-relativistic form, it is called the Yukawa potential. The pion, being spinless, has kinematics described by the Klein–Gordon equation. In the terms of quantum field theory, the effective field theory Lagrangian describing the pion-nucleon interaction is called the Yukawa interaction.

The nearly identical masses of
π^± and
π⁰ imply that there must be a symmetry at play; this symmetry is called the SU(2) flavour symmetry or isospin. The reason that there are three pions,
π⁺,
π⁻ and
π⁰, is that these are understood to belong to the triplet representation or the adjoint representation 3 of SU(2). By contrast, the up and down quarks transform according to the fundamental representation 2 of SU(2), whereas the anti-quarks transform according to the conjugate representation 2*.

With the addition of the strange quark, one can say that the pions participate in an SU(3) flavour symmetry, belonging to the adjoint representation 8 of SU(3). The other members of this octet are the four kaons and the eta meson.

Pions are pseudoscalars under a parity transformation. Pion currents thus couple to the axial vector current and pions participate in the chiral anomaly.

Basic properties

Pions, which are mesons with zero spin, are composed of first-generation quarks. In the quark model, an up quark and an anti-down quark make up a
π⁺, whereas a down quark and an anti-up quark make up the
π⁻, and these are the antiparticles of one another. The neutral pion
π⁰ is a combination of an up quark with an anti-up quark or a down quark with an anti-down quark. The two combinations have identical quantum numbers, and hence they are only found in superpositions. The lowest-energy superposition of these is the
π⁰, which is its own antiparticle. Together, the pions form a triplet of isospin. Each pion has isospin (I = 1) and third-component isospin equal to its charge (I_z = +1, 0 or −1).

Charged pion decays

Feynman diagram of the dominating leptonic pion decay.

The
π^± mesons have a mass of 139.6 MeV/c² and a mean lifetime of 2.6033×10⁻⁸ s. They decay due to the weak interaction. The primary decay mode of a pion, with a branching fraction of 0.999877, is a leptonic decay into a muon and a muon neutrino:

π+	→	μ+	+	ν μ
π−	→	μ−	+	ν μ

The second most common decay mode of a pion, with a branching fraction of 0.000123, is also a leptonic decay into an electron and the corresponding electron antineutrino. This "electronic mode" was discovered at CERN in 1958:^[6]

π+	→	e+	+	ν e
π−	→	e−	+	ν e

The suppression of the electronic decay mode with respect to the muonic one is given approximately (up to a few percent effect of the radiative corrections) by the ratio of the half-widths of the pion–electron and the pion–muon decay reactions:

${\displaystyle R_{\pi }=(m_{e}/m_{\mu })^{2}\left({\frac {m_{\pi }^{2}-m_{e}^{2}}{m_{\pi }^{2}-m_{\mu }^{2}}}\right)^{2}=1.283\times 10^{-4}}$

and is a spin effect known as helicity suppression. Its mechanism is as follows: The negative pion has spin zero, therefore the lepton and antineutrino must be emitted with opposite spins (and opposite linear momenta) to preserve net zero spin (and conserve linear momentum). However, because the weak interaction is sensitive only to the left chirality component of fields, the antineutrino has always chirality left, which means it is right-handed, since for massless anti-particles the helicity is opposite to the chirality. This implies that the lepton must be emitted with spin in the direction of its linear momentum (i.e., also right-handed). If, however, leptons were massless, they would only interact with the pion in the left-handed form (because for massless particles helicity is the same as chirality) and this decay mode would be prohibited. Therefore, suppression of the electron decay channel comes from the fact that the electron's mass is much smaller than the muon's. The electron is thus relatively massless compared with the muon, and thus the electronic mode is almost prohibited.^[7] Although this explanation suggests that parity violation is causing the helicity suppression, it should be emphasized that the fundamental reason lies in the vector-nature of the interaction which demands a different handedness for the neutrino and the charged lepton. Thus, even a parity conserving interaction would yield the same suppression.

Measurements of the above ratio have been considered for decades to be a test of lepton universality. Experimentally, this ratio is 1.230(4)×10⁻⁴.^[8]

Besides the purely leptonic decays of pions, some structure-dependent radiative leptonic decays (that is, decay to the usual leptons plus a gamma ray) have also been observed.

Also observed, for charged pions only, is the very rare "pion beta decay" (with branching fraction of about 10⁻⁸) into a neutral pion, an electron and an electron antineutrino (or for positive pions, a neutral pion, a positron, and electron neutrino).

π−	→	π0	+	e−	+	ν e
π+	→	π0	+	e+	+	ν e

The rate at which pions decay is a prominent quantity in many sub-fields of particle physics, such as chiral perturbation theory. This rate is parametrized by the pion decay constant (ƒ_π), related to the wave function overlap of the quark and antiquark, which is about 130 MeV.^[9]

Neutral pion decays

The
π⁰ meson has a mass of 135.0 MeV/c² and a mean lifetime of 8.4×10⁻¹⁷ s. It decays via the electromagnetic force, which explains why its mean lifetime is much smaller than that of the charged pion (which can only decay via the weak force). The main π⁰ decay mode, with a branching ratio of BR=0.98823, is into two photons:

π0

→

2 γ .

The decay π⁰ → 3γ (as well as decays into any odd number of photons) is forbidden by the C-symmetry of the electromagnetic interaction. The intrinsic C-parity of the π⁰ is +1, while the C-parity of a system of n photons is (−1)ⁿ.

The second largest π⁰ decay mode (BR=0.01174) is the Dalitz decay (named after Richard Dalitz), which is a two-photon decay with an internal photon conversion resulting a photon and an electron-positron pair in the final state:

π0

→

γ

+

e−

+

e+.

The third largest established decay mode (BR=3.34×10⁻⁵) is the double Dalitz decay, with both photons undergoing internal conversion which leads to further suppression of the rate:

π0

→

e−

+

e+

+

e−

+

e+.

The fourth largest established decay mode is the loop-induced and therefore suppressed (and additionally helicity-suppressed) leptonic decay mode (BR=6.46×10⁻⁸):

π0

→

e−

+

e+.

The neutral pion has also been observed to decay into positronium with a branching fraction of the order of 10⁻⁹. No other decay modes have been established experimentally. The branching fractions above are the PDG central values, and their uncertainties are not quoted.

Pions

Particle name	Particle symbol	Antiparticle symbol	Quark content[10]	Rest mass (MeV/c2)	IG	JPC	S	C	B'	Mean lifetime (s)	Commonly decays to (>5% of decays)
Pion[8]	π+	π−	u d	139.570 18 ± 0.000 35	1−	0−	0	0	0	2.6033 ± 0.0005 × 10−8	μ+ + ν μ
Pion[11]	π0	Self	${\displaystyle {\tfrac {\mathrm {u{\bar {u}}} -\mathrm {d{\bar {d}}} }{\sqrt {2}}}}$[a]	134.976 6 ± 0.000 6	1−	0−+	0	0	0	8.4 ± 0.6 × 10−17	γ + γ

^[a] ^ Make-up inexact due to non-zero quark masses.

New chemical method could revolutionize graphene use in electronics

June 16, 2017
Original link:  http://www.kurzweilai.net/new-chemical-method-could-revolutionize-graphene-use-in-electronics

Adding a molecular structure containing carbon, chromium, and oxygen atoms retains graphene’s superior conductive properties. The metal atoms (silver, in this experiment) to be bonded are then added to the oxygen atoms on top. (credit: Songwei Che et al./Nano Letters)

University of Illinois at Chicago scientists have solved a fundamental problem that has held back the use of wonder material graphene in a wide variety of electronics applications.

When graphene is bonded (attached) to metal atoms (such as molybdenum) in devices such as solar cells, graphene’s superior conduction properties degrade.

The solution: Instead of adding molecules directly to the individual carbon atoms of graphene, the new method first adds a sort of buffer (consisting of chromium, carbon, and oxygen atoms) to the graphene, and then adds the metal atoms to this buffer material instead. That enables the graphene to retain its unique properties of electrical conduction.

In an experiment, the researchers successfully added silver nanoparticles to graphene with this method. That increased the material’s ability to boost the efficiency of graphene-based solar cells by 11 fold, said Vikas Berry, associate professor and department head of chemical engineering and senior author of a paper on the research, published in Nano Letters.

Researchers at Indian Institute of Technology and Clemson University were also involved in the study. The research was funded by the National Science Foundation.

---

Abstract of Retained Carrier-Mobility and Enhanced Plasmonic-Photovoltaics of Graphene via ring-centered η⁶ Functionalization and Nanointerfacing

Binding graphene with auxiliary nanoparticles for plasmonics, photovoltaics, and/or optoelectronics, while retaining the trigonal-planar bonding of sp² hybridized carbons to maintain its carrier-mobility, has remained a challenge. The conventional nanoparticle-incorporation route for graphene is to create nucleation/attachment sites via “carbon-centered” covalent functionalization, which changes the local hybridization of carbon atoms from trigonal-planar sp²to tetrahedral sp³. This disrupts the lattice planarity of graphene, thus dramatically deteriorating its mobility and innate superior properties. Here, we show large-area, vapor-phase, “ring-centered” hexahapto (η⁶) functionalization of graphene to create nucleation-sites for silver nanoparticles (AgNPs) without disrupting its sp² character. This is achieved by the grafting of chromium tricarbonyl [Cr(CO)₃] with all six carbon atoms (sigma-bonding) in the benzenoid ring on graphene to form an (η⁶-graphene)Cr(CO)₃ complex. This nondestructive functionalization preserves the lattice continuum with a retention in charge carrier mobility (9% increase at 10 K); with AgNPs attached on graphene/n-Si solar cells, we report an ∼11-fold plasmonic-enhancement in the power conversion efficiency (1.24%).

References:

• Songwei Che, Kabeer Jasuja, Sanjay K. Behura, Phong Nguyen, T. S. Sreeprasad, and Vikas Berry. Retained Carrier-Mobility and Enhanced Plasmonic-Photovoltaics of Graphene via ring-centered η6 Functionalization and Nanointerfacing. Nano Lett., 2017 DOI: 10.1021/acs.nanolett.7b01458

Gravitational interaction of antimatter

From Wikipedia, the free encyclopedia

 

The gravitational interaction of antimatter with matter or antimatter has not been conclusively observed by physicists. While the consensus among physicists is that gravity will attract both matter and antimatter at the same rate that matter attracts matter, there is a strong desire to confirm this experimentally.

Antimatter's rarity and tendency to annihilate when brought into contact with matter makes its study a technically demanding task. Most methods for the creation of antimatter (specifically antihydrogen) result in high-energy particles and atoms of high kinetic energy, which are unsuitable for gravity-related study. In recent years, first ALPHA^[1][2] and then ATRAP^[3] have trapped antihydrogen atoms at CERN; in 2012 ALPHA used such atoms to set the first free-fall loose bounds on the gravitational interaction of antimatter with matter, measured to within ±7500% of ordinary gravity^[4], not enough for a clear scientific statement about the sign of gravity acting on antimatter. Future experiments need to be performed with higher precision, either with beams of antihydrogen (AEGIS) or with trapped antihydrogen (ALPHA or GBAR).

Three hypotheses

Thus far, there are three hypotheses about how antimatter gravitationally interacts with normal matter:

• Normal gravity: The standard assumption is that gravitational interactions of matter and antimatter are identical.
• Antigravity: Some authors argue that antimatter repels matter with the same magnitude as matter attracts itself. (see below).
• Gravivector and graviscalar: Later difficulties in creating quantum gravity theories have led to the idea that antimatter may react with a slightly different magnitude.^[5]

Experiments

Supernova 1987A

One source of experimental evidence in favor of normal gravity was the observation of neutrinos from Supernova 1987A. In 1987, three neutrino detectors around the world simultaneously observed a cascade of neutrinos emanating from a supernova in the Large Magellanic Cloud. Although the supernova happened about 164,000 light years away, both neutrinos and antineutrinos seem to have been detected virtually simultaneously^{[clarification needed]}. If both were actually observed, then any difference in the gravitational interaction would have to be very small. However, neutrino detectors cannot distinguish perfectly between neutrinos and antineutrinos; in fact, the two may be identical. Some physicists conservatively estimate that there is less than a 10% chance that no regular neutrinos were observed at all. Others estimate even lower probabilities, some as low as 1%.^[6] Unfortunately, this accuracy is unlikely to be improved by duplicating the experiment any time soon. The last known supernova to occur at such a close range prior to Supernova 1987A was around 1867.^[7]

Fairbank's experiments

Physicist William Fairbank attempted a laboratory experiment to directly measure the gravitational acceleration of both electrons and positrons. However, their charge-to-mass ratio is so large that electromagnetic effects overwhelmed the experiment.

It is difficult to directly observe gravitational forces at the particle level. For charged particles, the electromagnetic force overwhelms the much weaker gravitational interaction. Even antiparticles in neutral antimatter, such as antihydrogen, must be kept separate from their counterparts in the matter that forms the experimental equipment, which requires strong electromagnetic fields. These fields, e.g. in the form of atomic traps, exert forces on these antiparticles which easily overwhelm the gravitational force of Earth and nearby test masses. Since all production methods for antiparticles result in high-energy antimatter particles, the necessary cooling for observation of gravitational effects in a laboratory environment requires very elaborate experimental techniques and very careful control of the trapping fields.

Cold neutral antihydrogen experiments

Since 2010 the production of cold antihydrogen has become possible at the Antiproton Decelerator at CERN. Antihydrogen, which is electrically neutral, should make it possible to directly measure the gravitational attraction of antimatter particles to the matter Earth. In 2013, experiments on antihydrogen atoms released from the ALPHA trap set direct, i.e. freefall, coarse limits on antimatter gravity.^[4] These limits were coarse, with a relative precision of ± 100%, thus, far from a clear statement even for the sign of gravity acting on antimatter. Future experiments at CERN with beams of antihydrogen, such as AEGIS, or with trapped antihydrogen, such as ALPHA and GBAR, have to improve the sensitivity to make a clear, scientific statement about gravity on antimatter.^[8]

Superconductor-positron interactions

A hypothesis originally suggested by early experiments with positron interactions with HTSCs suggests that under certain conditions the weak hypothetical antigravitational fields of the positrons could form into a beam. If so then a relatively simple device consisting of a YBCO or BSCCO disk with acoustic coupling to three or more ultrasonic transducers set up so that the vibrational pattern of the Cooper pair generating domains rotate or precess around the centre axis under a weak electrical bias could form such a beam and be detected with relatively simple Peltier-cooled linear accelerometers common to cellphones and other devices. ^[9] A pair of atomic clocks (eg Rb modules used as primary standards) with one placed in the beam and the other used as an absolute reference with both powered by independent batteries using no magnetic components (ie lead acid) should over time show a discrepancy, going well beyond that expected for a magnetic field. This would also scale with distance so at twice the distance you would expect to see 1/4 of the effect due to the inverse square law. As this in itself would be new physics it is not clear if this would have significant effects on large amounts of antimatter in nature, if the antiparticles were also entangled there could be a larger effect on cosmological scales.

Arguments against a gravitational repulsion of matter and antimatter

When antimatter was first discovered in 1932, physicists wondered about how it would react to gravity. Initial analysis focused on whether antimatter should react the same as matter or react oppositely. Several theoretical arguments arose which convinced physicists that antimatter would react exactly the same as normal matter. They inferred that a gravitational repulsion between matter and antimatter was implausible as it would violate CPT invariance, conservation of energy, result in vacuum instability, and result in CP violation. It was also theorized that it would be inconsistent with the results of the Eötvös test of the weak equivalence principle. Many of these early theoretical objections were later overturned.^[10]

The equivalence principle

The equivalence principle predicts that the gravitational acceleration of antimatter is the same as that of ordinary matter. A matter-antimatter gravitational repulsion is thus excluded from this point of view. Furthermore, photons, which are their own antiparticles in the framework of the Standard Model, have in a large number of astronomical tests (gravitational redshift and gravitational lensing, for example) been observed to interact with the gravitational field of ordinary matter exactly as predicted by the general theory of relativity. This is a feature that has to be explained by any theory predicting that matter and antimatter repel.

CPT theorem

The CPT theorem implies that the difference between the properties of a matter particle and those of its antimatter counterpart is completely described by C-inversion. Since this C-inversion doesn't affect gravitational mass, the CPT theorem predicts that the gravitational mass of antimatter is the same as that of ordinary matter.^[11] A repulsive gravity is then excluded, since that would imply a difference in sign between the observable gravitational mass of matter and antimatter.

Morrison's argument

In 1958, Philip Morrison argued that antigravity would violate conservation of energy. If matter and antimatter responded oppositely to a gravitational field, then it would take no energy to change the height of a particle-antiparticle pair. However, when moving through a gravitational potential, the frequency and energy of light is shifted. Morrison argued that energy would be created by producing matter and antimatter at one height and then annihilating it higher up, since the photons used in production would have less energy than the photons yielded from annihilation.^[12] However, it was later found that antigravity would still not violate the second law of thermodynamics.^[13]

Schiff's argument

Later in 1958, L. Schiff used quantum field theory to argue that antigravity would be inconsistent with the results of the Eötvös experiment.^[14] However, the renormalization technique used in Schiff's analysis is heavily criticized, and his work is seen as inconclusive.^[10] In 2014 the argument was redone by Cabbolet, who concluded however that it merely demonstrates the incompatibility of the Standard Model and gravitational repulsion.^[15]

Good's argument

In 1961, Myron L. Good argued that antigravity would result in the observation of an unacceptably high amount of CP violation in the anomalous regeneration of kaons.^[16] At the time, CP violation had not yet been observed. However, Good's argument is criticized for being expressed in terms of absolute potentials. By rephrasing the argument in terms of relative potentials, Gabriel Chardin found that it resulted in an amount of kaon regeneration which agrees with observation.^[17] He argues that antigravity is in fact a potential explanation for CP violation based on his models on K mesons. His results date back to 1992. Since then however, studies on CP violation mechanisms in the B mesons systems have fundamentally invalidated these explanations.

Gerard 't Hooft's argument

According to Gerard 't Hooft, every physicist recognizes immediately what is wrong with the idea of gravitational repulsion: if a ball is thrown high up in the air so that it falls back, then its motion is symmetric under time-reversal; and therefore, the ball falls also down in opposite time-direction.^[18] Since a matter particle in opposite time-direction is an antiparticle, this proves according to 't Hooft that antimatter falls down on earth just like "normal" matter. However, Cabbolet replied that 't Hooft's argument is false, and only proves that an anti-ball falls down on an anti-earth – which is not disputed.^[19]

Theories of gravitational repulsion

As long as repulsive gravity has not been refuted experimentally, one can speculate about physical principles that would bring about such a repulsion. Thus far, three radically different theories have been published:

• The first theory of repulsive gravity was a quantum theory published by Kowitt.^[20] In this modified Dirac theory, Kowitt postulated that the positron is not a hole in the sea of electrons-with-negative-energy as in usual Dirac hole theory, but instead is a hole in the sea of electrons-with-negative-energy-and-positive-gravitational-mass: this yields a modified C-inversion, by which the positron has positive energy but negative gravitational mass. Repulsive gravity is then described by adding extra terms (m_gΦ_g and m_gA_g) to the wave equation. The idea is that the wave function of a positron moving in the gravitational field of a matter particle evolves such that in time it becomes more probable to find the positron further away from the matter particle.
• Classical theories of repulsive gravity have been published by Santilli and Villata.^{[21][22][23][24]} Both theories are extensions of General Relativity, and are experimentally indistinguishable. The general idea remains that gravity is the deflection of a continuous particle trajectory due to the curvature of spacetime, but antiparticles now 'live' in an inverted spacetime. The equation of motion for antiparticles is then obtained from the equation of motion of ordinary particles by applying the C, P, and T-operators (Villata) or by applying isodual maps (Santilli), which amounts to the same thing: the equation of motion for antiparticles then predicts a repulsion of matter and antimatter. It has to be taken that the observed trajectories of antiparticles are projections on our spacetime of the true trajectories in the inverted spacetime. However, it has been argued on methodological and ontological grounds that the area of application of Villata’s theory cannot be extended to include the microcosmos.^[25] These objections were subsequently dismissed by Villata.^[26]
• The first non-classical, non-quantum physical principles underlying a matter-antimatter gravitational repulsion have been published by Cabbolet.^[11][27] He introduces the Elementary Process Theory, which uses a new language for physics, i.e. a new mathematical formalism and new physical concepts, and which is incompatible with both quantum mechanics and general relativity. The core idea is that nonzero rest mass particles such as electrons, protons, neutrons and their antimatter counterparts exhibit stepwise motion as they alternate between a particlelike state of rest and a wavelike state of motion. Gravitation then takes place in a wavelike state, and the theory allows, for example, that the wavelike states of protons and antiprotons interact differently with the earth’s gravitational field.

Further authors^[28][29][30] have used a matter-antimatter gravitational repulsion to explain cosmological observations, but these publications do not address the physical principles of gravitational repulsion.