The globular cluster M80. Stars in globular clusters are mainly older metal-poor members of Population II.
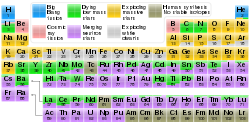
In astronomy, metallicity is used to describe the abundance of elements present in an object that are heavier than hydrogen or helium. Most of the physical matter in the Universe is in the form of hydrogen and helium, so astronomers
use the word "metals" as a convenient short term for "all elements
except hydrogen and helium". This usage is distinct from the usual
physical definition of a solid metal. For example, stars and nebulae with relatively high abundances of carbon, nitrogen, oxygen, and neon are called "metal-rich" in astrophysical terms, even though those elements are non-metals in chemistry.
The presence of heavier elements hails from stellar nucleosynthesis,
the theory that the majority of elements heavier than hydrogen and
helium in the Universe ("metals", hereafter) are formed in the cores of
stars as they evolve. Over time, stellar winds and supernovae deposit the metals into the surrounding environment, enriching the interstellar medium and providing recycling materials for the birth of new stars. It follows that older generations of stars, which formed in the metal-poor early Universe, generally have lower metallicities than those of younger generations, which formed in a more metal-rich Universe.
Observed changes in the chemical abundances of different types of
stars, based on the spectral peculiarities that were later attributed
to metallicity, led astronomer Walter Baade in 1944 to propose the existence of two different populations of stars.
These became commonly known as Population I (metal-rich) and Population II (metal-poor) stars. A third stellar population was introduced in 1978, known as Population III stars. These extremely metal-poor stars were theorised to have been the "first-born" stars created in the Universe.
Common methods of calculation
Astronomers
use several different methods to describe and approximate metal
abundances, depending on the available tools and the object of interest.
Some methods include determining the fraction of mass that is
attributed to gas versus metals, or measuring the ratios of the number of atoms of two different elements as compared to the ratios found in the Sun.
Mass fraction
Stellar composition is often simply defined by the parameters X, Y and Z. Here X is the mass fraction of hydrogen, Y is the mass fraction of helium, and Z is the mass fraction of all the remaining chemical elements. Thus
In most stars, nebulae, H II regions,
and other astronomical sources, hydrogen and helium are the two
dominant elements. The hydrogen mass fraction is generally expressed as , where is the total mass of the system, and is the fractional mass of the hydrogen it contains. Similarly, the helium mass fraction is denoted as .
The remainder of the elements are collectively referred to as "metals",
and the metallicity—the mass fraction of elements heavier than
helium—can be calculated as
For the surface of the Sun, these parameters are measured to have the following values:
Description Solar value Hydrogen mass fraction Helium mass fraction Metallicity
Due to the effects of stellar evolution,
neither the initial composition nor the present day bulk composition of
the Sun is the same as its present-day surface composition.
Chemical abundance ratios
The overall stellar metallicity is often defined using the total iron content of the star, as iron is among the easiest to measure with spectral observations in the visible spectrum (even though oxygen is the most abundant heavy element – see metallicities in HII regions below). The abundance ratio is defined as the logarithm of the ratio of a star's iron abundance compared to that of the Sun and is expressed thus:
where and are the number of iron and hydrogen atoms per unit of volume respectively. The unit often used for metallicity is the dex, contraction of "decimal exponent". By this formulation, stars with a higher metallicity than the Sun have a positive logarithmic
value, whereas those with a lower metallicity than the Sun have a
negative value. For example, stars with a [Fe/H] value of +1 have 10
times the metallicity of the Sun (101); conversely, those
with a [Fe/H] value of −1 have 1/10, while those with a [Fe/H] value of 0
have the same metallicity as the Sun, and so on.
Young Population I stars have significantly higher iron-to-hydrogen
ratios than older Population II stars. Primordial Population III stars
are estimated to have a metallicity of less than −6.0, that is, less
than a millionth of the abundance of iron in the Sun.
The same notation is used to express variations in abundances
between other the individual elements as compared to solar proportions.
For example, the notation "[O/Fe]" represents the difference in the
logarithm of the star's oxygen abundance versus its iron content
compared to that of the Sun. In general, a given stellar nucleosynthetic
process alters the proportions of only a few elements or isotopes, so a
star or gas sample with nonzero [X/Fe] values may be showing the
signature of particular nuclear processes.
Photometric colors
Astronomers can estimate metallicities through measured and calibrated systems that correlate photometric measurements and spectroscopic measurements. For example, the Johnson UVB filters can be used to detect an ultraviolet (UV) excess in stars, where a larger UV excess indicates a larger presence of metals that absorb the UV radiation, thereby making the star appear "redder". The UV excess, δ(U−B), is defined as the difference between a star's U and B band magnitudes, compared to the difference between U and B band magnitudes of metal-rich stars in the Hyades cluster. Unfortunately, δ(U−B) is sensitive to both metallicity and temperature: if two stars are equally metal-rich, but one is cooler than the other, they will likely have different δ(U−B) values. To help mitigate this degeneracy, a star's B−V color
can be used as an indicator for temperature. Furthermore, the UV excess
and B−V color can be corrected to relate the δ(U−B) value to iron
abundances.
Other photometric systems that can be used to determine metallicities of certain astrophysical objects include the Strӧmgren system, the Geneva system, the Washington system, and the DDO system.
Metallicities in various astrophysical objects
Stars
Relationship between stellar metallicity and planets
A star's metallicity measurement is one parameter that helps determine whether a star has planets
and the type of planets, as there is a direct correlation between
metallicity and the type of planets a star may have. Measurements have
demonstrated the connection between a star's metallicity and gas giant planets, like Jupiter and Saturn. The more metals in a star and thus its planetary system and proplyd, the more likely the system may have gas giant planets and rocky planets.
Current models show that the metallicity along with the correct
planetary system temperature and distance from the star are key to
planet and planetesimal formation. For two stars that have equal age and mass but different metallicity, the less metallic star is bluer. Among stars of the same color, less metallic stars emit more ultraviolet radiation. The Sun, with 8 planets and 5 known dwarf planets, is used as the reference, with a [Fe/H] of 0.00.
HII regions
Young, massive and hot stars (typically of spectral types O and B) in H II regions emit UV photons that ionize ground-state hydrogen atoms, knocking electrons and protons free; this process is known as photoionization. The free electrons can strike other atoms nearby, exciting bound metallic electrons into a metastable state, which eventually decay back into a ground state, emitting photons with energies that correspond to forbidden lines.
Through these transitions, astronomers have developed several
observational methods to estimate metal abundances in HII regions, where
the stronger the forbidden lines in spectroscopic observations, the
higher the metallicity.
These methods are dependent on one or more of the following: the
variety of asymmetrical densities inside HII regions, the varied
temperatures of the embedded stars, and/or the electron density within
the ionized region.
Theoretically, to determine the total abundance of a single
element in an HII region, all transition lines should be observed and
summed. However, this can be observationally difficult due to variation
in line strength. Some of the most common forbidden lines used to determine metal abundances in HII regions are from oxygen (e.g. [O II] λ = (3727, 7318, 7324) Å, and [O III] λ = (4363, 4959, 5007) Å, nitrogen (e.g. [NII] λ = (5755, 6548, 6584) Å), and sulfur (e.g. [SII] λ = (6717,6731) Å and [SIII] λ = (6312, 9069, 9531) Å) in the optical spectrum, and the [OIII] λ = (52, 88) μm and [NIII] λ = 57 μm lines in the infrared spectrum. Oxygen
has some of the stronger, more abundant lines in HII regions, making it
a main target for metallicity estimates within these objects. To
calculate metal abundances in HII regions using oxygen flux measurements, astronomers often use the R23 method, in which
where is the sum of the fluxes from oxygen emission lines measured at the rest frame λ = (3727, 4959 and 5007) Å wavelengths, divided by the flux from the Hβ emission line at the rest frame λ = 4861 Å wavelength. This ratio is well defined through models and observational studies,
but caution should be taken, as the ratio is often degenerate,
providing both a low and high metallicity solution, which can be broken
with additional line measurements. Similarly, other strong forbidden line ratios can be used, e.g. for sulfur, where
Metal abundances within HII regions are typically less than 1%, with
the percentage decreasing on average with distance from the Galactic Center.








![{\displaystyle R_{23}={\frac {[{\text{O II}}]_{3727~\mathrm {\AA} }+[{\text{O III}}]_{4959~\mathrm {\AA} +5007~\mathrm {\AA} }}{{\text{H}}_{\beta }}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/382a2b4bcb84669d0134a5e586f5db12b701d2cc)

![{\displaystyle S_{23}={\frac {[{\text{S II}}]_{6716~\mathrm {\AA} +6731~\mathrm {\AA} }+[{\text{S III}}]_{9069~\mathrm {\AA} +9532~\mathrm {\AA} }}{{\text{H}}_{\beta }}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28d1263d77e71ad861598be690c740f6350b9dff)