The phase-space formulation of quantum mechanics places the position and momentum variables on equal footing, in phase space. In contrast, the Schrödinger picture uses the position or momentum representations (see also position and momentum space). The two key features of the phase-space formulation are that the quantum state is described by a quasiprobability distribution (instead of a wave function, state vector, or density matrix) and operator multiplication is replaced by a star product.
The theory was fully developed by Hilbrand Groenewold in 1946 in his PhD thesis, and independently by Joe Moyal, each building on earlier ideas by Hermann Weyl[3] and Eugene Wigner.
The chief advantage of the phase-space formulation is that it makes quantum mechanics appear as similar to Hamiltonian mechanics as possible by avoiding the operator formalism, thereby "'freeing' the quantization of the 'burden' of the Hilbert space". This formulation is statistical in nature and offers logical connections between quantum mechanics and classical statistical mechanics, enabling a natural comparison between the two. Quantum mechanics in phase space is often favored in certain quantum optics applications, or in the study of decoherence and a range of specialized technical problems, though otherwise the formalism is less commonly employed in practical situations.
The conceptual ideas underlying the development of quantum mechanics in phase space have branched into mathematical offshoots such as algebraic deformation theory (see Kontsevich quantization formula) and noncommutative geometry.
Phase-space distribution
The phase-space distribution f(x, p)
of a quantum state is a quasiprobability distribution. In the
phase-space formulation, the phase-space distribution may be treated as
the fundamental, primitive description of the quantum system, without
any reference to wave functions or density matrices.
There are several different ways to represent the distribution, all interrelated. The most noteworthy is the Wigner representation, W(x, p), discovered first. Other representations (in approximately descending order of prevalence in the literature) include the Glauber–Sudarshan P, Husimi Q, Kirkwood–Rihaczek, Mehta, Rivier, and Born–Jordan representations. These alternatives are most useful when the Hamiltonian takes a particular form, such as normal order
for the Glauber–Sudarshan P-representation. Since the Wigner
representation is the most common, this article will usually stick to
it, unless otherwise specified.
The phase-space distribution possesses properties akin to the probability density in a 2n-dimensional phase space. For example, it is real-valued,
unlike the generally complex-valued wave function. We can understand
the probability of lying within a position interval, for example, by
integrating the Wigner function over all momenta and over the position
interval:
If Â(x, p) is an operator representing an observable, it may be mapped to phase space as A(x, p) through the Wigner transform. Conversely, this operator may be recovered by the Weyl transform.
The expectation value of the observable with respect to the phase-space distribution is
A point of caution, however: despite the similarity in appearance, W(x, p) is not a genuine joint probability distribution, because regions under it do not represent mutually exclusive states, as required in the third axiom of probability theory. Moreover, it can, in general, take negative values even for pure states, with the unique exception of (optionally squeezed) coherent states, in violation of the first axiom.
Regions of such negative value are provable to be "small": they cannot extend to compact regions larger than a few ħ, and hence disappear in the classical limit. They are shielded by the uncertainty principle, which does not allow precise localization within phase-space regions smaller than ħ,
and thus renders such "negative probabilities" less paradoxical. If
the left side of the equation is to be interpreted as an expectation
value in the Hilbert space with respect to an operator, then in the
context of quantum optics this equation is known as the optical equivalence theorem.
An alternative phase-space approach to quantum mechanics seeks to
define a wave function (not just a quasiprobability density) on phase
space, typically by means of the Segal–Bargmann transform.
To be compatible with the uncertainty principle, the phase-space wave
function cannot be an arbitrary function, or else it could be localized
into an arbitrarily small region of phase space. Rather, the
Segal–Bargmann transform is a holomorphic function of . There is a quasiprobability density associated to the phase-space wave function; it is the Husimi Q representation of the position wave function.
Star product
The fundamental noncommutative binary operator in the phase space
formulation that replaces the standard operator multiplication is the star product, represented by the symbol ★. Each representation of the phase-space distribution has a different
characteristic star product. For concreteness, we restrict this
discussion to the star product relevant to the Wigner-Weyl
representation.
For notational convenience, we introduce the notion of left and right derivatives. For a pair of functions f and g, the left and right derivatives are defined as
The differential definition of the star product is
where the argument of the exponential function can be interpreted as a power series.
Additional differential relations allow this to be written in terms of a change in the arguments of f and g:
It is also possible to define the ★-product in a convolution integral form, essentially through the Fourier transform:
(Thus, e.g., Gaussians compose hyperbolically,
or
etc.)
The energy eigenstate distributions are known as stargenstates, ★-genstates, stargenfunctions, or ★-genfunctions, and the associated energies are known as stargenvalues or ★-genvalues. These are solved, analogously to the time-independent Schrödinger equation, by the ★-genvalue equation,
where H is the Hamiltonian, a plain phase-space function, most often identical to the classical Hamiltonian.
Time evolution
The time evolution of the phase space distribution is given by a quantum modification of Liouville flow. This formula results from applying the Wigner transformation to the density matrix version of the quantum Liouville equation,
the von Neumann equation.
In any representation of the phase space distribution with its associated star product, this is
or, for the Wigner function in particular,
where {{ , }} is the Moyal bracket, the Wigner transform of the quantum commutator, while { , } is the classical Poisson bracket.
This yields a concise illustration of the correspondence principle: this equation manifestly reduces to the classical Liouville equation in the limit ħ → 0. In the quantum extension of the flow, however, the density of points in phase space is not conserved; the probability fluid appears "diffusive" and compressible.
The concept of quantum trajectory is therefore a delicate issue here. (Given the restrictions placed by the uncertainty principle on localization, Niels Bohr
vigorously denied the physical existence of such trajectories on the
microscopic scale. By means of formal phase-space trajectories, the time
evolution problem of the Wigner function can be rigorously solved using
the path-integral method and the method of quantum characteristics,
although there are practical obstacles in both cases.) See the movie
for the Morse potential, below, to appreciate the nonlocality of quantum
phase flow.
Examples
Simple harmonic oscillator
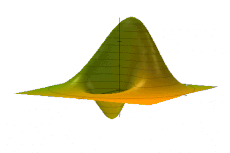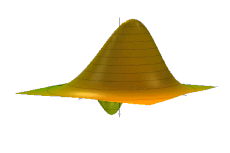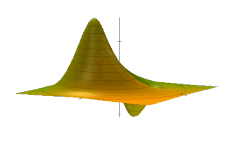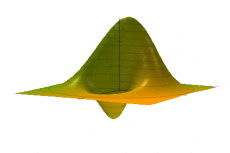
The Wigner quasiprobability distribution Fn(u) for the simple harmonic oscillator with a) n = 0, b) n = 1, and c) n = 5.
The Hamiltonian for the simple harmonic oscillator in one spatial dimension in the Wigner-Weyl representation is
The ★-genvalue equation for the static Wigner function then reads
Time
evolution of combined ground and 1st excited state Wigner function for
the simple harmonic oscillator. Note the rigid motion in phase space
corresponding to the conventional oscillations in coordinate space.
Wigner function for the harmonic oscillator ground state, displaced from the origin of phase space, i.e., a coherent state. Note the rigid rotation, identical to classical motion: this is a special feature of the SHO, illustrating the correspondence principle. From the general pedagogy web-site.
This implies that one may write the ★-genstates as functions of a single argument,
With this change of variables, it is possible to write the real part of the ★-genvalue equation in the form of a modified Laguerre equation (not Hermite's equation!), the solution of which involves the Laguerre polynomials as
introduced by Groenewold in his paper, with associated ★-genvalues
For the harmonic oscillator, the time evolution of an arbitrary Wigner distribution is simple. An initial W(x,p; t = 0) = F(u) evolves by the above evolution equation driven by the oscillator Hamiltonian given, by simply rigidly rotating in phase space,
Typically, a "bump" (or coherent state) of energy E ≫ ħω can represent a macroscopic quantity and appear like a classical object rotating uniformly in phase space,
a plain mechanical oscillator (see the animated figures). Integrating over all phases (starting positions at t = 0) of such objects, a continuous "palisade", yields a time-independent configuration similar to the above static ★-genstates F(u), an intuitive visualization of the classical limit for large action systems.
Free particle angular momentum
Suppose a particle is initially in a minimally uncertain Gaussian state,
with the expectation values of position and momentum both centered at
the origin in phase space. The Wigner function for such a state
propagating freely is
where α is a parameter describing the initial width of the Gaussian, and τ = m/α2ħ.
Initially, the position and momenta are uncorrelated. Thus, in 3
dimensions, we expect the position and momentum vectors to be twice as
likely to be perpendicular to each other as parallel.
However, the position and momentum become increasingly
correlated as the state evolves, because portions of the distribution
farther from the origin in position require a larger momentum to be
reached: asymptotically,
(This relative "squeezing" reflects the spreading of the free wave packet in coordinate space.)
Indeed, it is possible to show that the kinetic energy of the
particle becomes asymptotically radial only, in agreement with the
standard
quantum-mechanical notion of the ground-state nonzero angular momentum
specifying orientation independence:
Morse potential
The Morse potential is used to approximate the vibrational structure of a diatomic molecule.

The Wigner function time-evolution of the Morse potential U(x) = 20(1 − e−0.16x)2 in atomic units (a.u.). The solid lines represent level set of the Hamiltonian H(x, p) = p2/2 + U(x).
Quantum tunneling
Tunneling
is a hallmark quantum effect where a quantum particle, not having
sufficient energy to fly above, still goes through a barrier. This
effect does not exist in classical mechanics.

The Wigner function for tunneling through the potential barrier U(x) = 8e−0.25x2 in atomic units (a.u.). The solid lines represent the level set of the Hamiltonian H(x, p) = p2/2 + U(x).
Quartic potential
The Wigner function time evolution for the potential U(x) = 0.1x4 in atomic units (a.u.). The solid lines represent the level set of the Hamiltonian H(x, p) = p2/2 + U(x).
Schrödinger cat state
Wigner
function of two interfering coherent states evolving through the SHO
Hamiltonian. The corresponding momentum and coordinate projections are
plotted to the right and under the phase space plot.
![\operatorname P [a \leq X \leq b] = \int_a^b \int_{-\infty}^{\infty} W(x, p) \, dp \, dx.](https://wikimedia.org/api/rest_v1/media/math/render/svg/517a35181dda6b6b75e0f5d115b3f76e9c18ade6)


![{\displaystyle {\begin{aligned}f{\overleftarrow {\partial }}_{x}g&={\frac {\partial f}{\partial x}}\cdot g\\[5pt]f{\overrightarrow {\partial }}_{x}g&=f\cdot {\frac {\partial g}{\partial x}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f424923d871036a4b1aea8971ba96dbfbfe6a3d)







![{\displaystyle {\begin{aligned}H\star W={}&\left({\frac {1}{2}}m\omega ^{2}x^{2}+{\frac {p^{2}}{2m}}\right)\star W\\[4pt]={}&\left({\frac {1}{2}}m\omega ^{2}\left(x+{\frac {i\hbar }{2}}{\stackrel {\rightarrow }{\partial }}_{p}\right)^{2}+{\frac {1}{2m}}\left(p-{\frac {i\hbar }{2}}{\stackrel {\rightarrow }{\partial }}_{x}\right)^{2}\right)~W\\[4pt]={}&\left({\frac {1}{2}}m\omega ^{2}\left(x^{2}-{\frac {\hbar ^{2}}{4}}{\stackrel {\rightarrow }{\partial }}_{p}^{2}\right)+{\frac {1}{2m}}\left(p^{2}-{\frac {\hbar ^{2}}{4}}{\stackrel {\rightarrow }{\partial }}_{x}^{2}\right)\right)~W\\[4pt]&{}+{\frac {i\hbar }{2}}\left(m\omega ^{2}x{\stackrel {\rightarrow }{\partial }}_{p}-{\frac {p}{m}}{\stackrel {\rightarrow }{\partial }}_{x}\right)~W\\[4pt]={}&E\cdot W.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68eedc00a922a8bc1fcbe6e0f926a229c44a4962)





![W \longrightarrow \frac{1}{(\pi\hbar)^3}\exp\left[-\alpha^2\left(\mathbf{x}-\frac{\mathbf{p}t}{m}\right)^2\right]\,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/4de73a30048e75e3a860e81b23c47ea7ce95dfb2)