Dynamic nuclear polarization (DNP) is one of several hyperpolarization methods developed to enhance the sensitivity of nuclear magnetic resonance (NMR) spectroscopy. While an essential analytical tool with applications in several fields, NMR’s low sensitivity poses major limitations to analyzing samples with low concentrations and limited masses and volumes. This low sensitivity is due to the relatively low nuclear gyromagnetic ratios (γn) of NMR active nuclei (1H, 13C, 15N, etc.) as well as the low natural abundance of certain nuclei. Several techniques have been developed to address this limitation, including hardware adjustments to NMR instruments and equipment (e.g., NMR tubes), improvements to data processing methods, and polarization transfer methods to NMR active nuclei in a sample—under which DNP falls.
Overhauser et al. were the first to hypothesize and describe the DNP effect in 1953; later that year, Carver and Slichter observed the effect in experiments using metallic lithium. DNP involves transferring the polarization of electron spins to neighboring nuclear spins using microwave irradiation at or near electron paramagnetic resonance (EPR) transitions. It is based on two fundamental concepts: first, that the electronic gyromagnetic moment (γe) is several orders of magnitude larger than γn (about 658 times more; see below), and second, that the relaxation of electron spins is much faster than nuclear spins.
,
where
is the Boltzmann equilibrium spin polarization. Note that the alignment of electron spins at a given magnetic field and temperature is described by the Boltzmann distribution under thermal equilibrium. A larger gyromagnetic moment corresponds to a larger Boltzmann distribution of populations in spin states; through DNP, the larger population distribution in the electronic spin reservoir is transferred to the neighboring nuclear spin reservoir, leading to stronger NMR signal intensities. The larger γ and faster relaxation of electron spins also help shorten T1 relaxation times of nearby nuclei, corresponding to stronger signal intensities.
Under ideal conditions (full saturation of electron spins and dipolar coupling without leakage to nuclear spins), the NMR signal enhancement for protons can at most be 659. This corresponds to a time-saving factor of 434,000 for a solution-phase NMR experiment. In general, the DNP enhancement parameter η is defined as:
where I is the signal intensity of the nuclear spins when the electron spins are saturated and I0 is the signal intensity of the nuclear spins when the electron spins are in equilibrium.

DNP methods typically fall under one of two categories: continuous wave DNP (CW-DNP) and pulsed DNP. As their names suggest, these methods differ in whether the sample is continuously irradiated or pulsed with microwaves. When electron spin polarization deviates from its thermal equilibrium value, polarization transfers between electrons and nuclei can occur spontaneously through electron-nuclear cross relaxation or spin-state mixing among electrons and nuclei. For example, polarization transfer is spontaneous after a homolysis chemical reaction. On the other hand, when the electron spin system is in a thermal equilibrium, the polarization transfer requires continuous microwave irradiation at a frequency close to the corresponding EPR frequency. It is also possible that electrons are aligned to a higher degree of order by other preparations of electron spin order such as chemical reactions (known as chemical-induced DNP or CIDNP), optical pumping, and spin injection. A polarizing agent (PA)—either an endogenous or exogenous paramagnetic system to the sample—is required as part of the DNP experimental setup. Typically, PAs are stable free radicals that are dissolved in solution or doped in solids; they provide a source of unpaired electrons that can be polarized by microwave radiation near the EPR transitions. DNP can also be induced using unpaired electrons produced by radiation damage in solids. Some common PAs are shown.
Described below are the four different mechanisms by which the DNP effect operates: the Overhauser effect (OE), the solid effect (SE), the cross effect (CE), and thermal mixing (TM). The DNP effect is present in solids and liquids and has been utilized successfully in solid-state and solution-phase NMR experiments. For solution-phase NMR experiments, only the OE mechanism is relevant, whereas for solid-state NMR any of the four mechanisms can be employed depending on the specific experimental conditions utilized.
The first DNP experiments were performed in the early 1950s at low magnetic fields but until recently the technique was of limited applicability for high-frequency, high-field NMR spectroscopy because of the lack of microwave (or terahertz) sources operating at the appropriate frequency. Today, such sources are available as turn-key instruments, making DNP a valuable and indispensable method especially in the field of structure determination by high-resolution solid-state NMR spectroscopy.
Mechanisms
Overhauser effect
DNP was first realized using the concept of the Overhauser effect, which is the perturbation of nuclear spin level populations observed in metals and free radicals when electron spin transitions are saturated by microwave irradiation. This effect relies on stochastic interactions between an electron and a nucleus. The "dynamic" initially meant to highlight the time-dependent and random interactions in this polarization transfer process.
The DNP phenomenon was theoretically predicted by Albert Overhauser in 1953 and initially drew some criticism from Norman Ramsey, Felix Bloch, and other renowned physicists of the time on the grounds of being "thermodynamically improbable". The experimental confirmation by Carver and Slichter as well as an apologetic letter from Ramsey both reached Overhauser in the same year.
The so-called electron-nucleus cross-relaxation, which is responsible for the DNP phenomenon is caused by rotational and translational modulation of the electron-nucleus hyperfine coupling. The theory of this process is based essentially on the second-order time-dependent perturbation theory solution of the von Neumann equation for the spin density matrix.
While the Overhauser effect relies on time-dependent electron-nuclear interactions, the remaining polarizing mechanisms rely on time-independent electron-nuclear and electron-electron interactions.
Solid effect
The simplest spin system exhibiting the SE DNP mechanism is an electron-nucleus spin pair. The Hamiltonian of the system can be written as:
These terms are referring respectively to the electron and nucleus Zeeman interaction with the external magnetic field, and the hyperfine interaction. S and I are the electron and nuclear spin operators in the Zeeman basis (spin 1⁄2 considered for simplicity), ωe and ωn are the electron and nuclear Larmor frequencies, and A and B are the secular and pseudo-secular parts of the hyperfine interaction. For simplicity we will only consider the case of |A|,|B|<<|ωn|. In such a case A has little effect on the evolution of the spin system. During DNP a MW irradiation is applied at a frequency ωMW and intensity ω1, resulting in a rotating frame Hamiltonian given by
- where
The MW irradiation can excite the electron single quantum transitions ("allowed transitions") when ωMW is close to ωe, resulting in a loss of the electron polarization. In addition, due to the small state mixing caused by the B term of the hyperfine interaction, it is possible to irradiate on the electron-nucleus zero quantum or double quantum ("forbidden") transitions around ωMW = ωe ± ωn, resulting in polarization transfer between the electrons and the nuclei. The effective MW irradiation on these transitions is approximately given by Bω1/2ωn.
Static sample case
In a simple picture of an electron-nucleus two-spin system, the solid effect occurs when a transition involving an electron-nucleus mutual flip (called zero quantum or double quantum) is excited by a microwave irradiation, in the presence of relaxation. This kind of transition is in general weakly allowed, meaning that the transition moment for the above microwave excitation results from a second-order effect of the electron-nuclear interactions and thus requires stronger microwave power to be significant, and its intensity is decreased by an increase of the external magnetic field B0. As a result, the DNP enhancement from the solid effect scales as B0−2 when all the relaxation parameters are kept constant. Once this transition is excited and the relaxation is acting, the magnetization is spread over the "bulk" nuclei (the major part of the detected nuclei in an NMR experiment) via the nuclear dipole network. This polarizing mechanism is optimal when the exciting microwave frequency shifts up or down by the nuclear Larmor frequency from the electron Larmor frequency in the discussed two-spin system. The direction of frequency shifts corresponds to the sign of DNP enhancements. Solid effect exist in most cases but is more easily observed if the linewidth of the EPR spectrum of involved unpaired electrons is smaller than the nuclear Larmor frequency of the corresponding nuclei.
Magic angle spinning case
In the case of magic angle spinning DNP (MAS-DNP), the mechanism is different but to understand it, a two spins system can still be used. The polarization process of the nucleus still occurs when the microwave irradiation excites the double quantum or zero quantum transition, but due to the fact that the sample is spinning, this condition is only met for a short time at each rotor cycle (which makes it periodical). The DNP process in that case happens step by step and not continuously as in the static case.
Cross effect
Static case
The cross effect requires two unpaired electrons as the source of high polarization. Without special condition, such a three spins system can only generate a solid effect type of polarization. However, when the resonance frequency of each electron is separated by the nuclear Larmor frequency, and when the two electrons are dipolar coupled, another mechanism occurs: the cross-effect. In that case, the DNP process is the result of irradiation of an allowed transition (called single quantum) as a result the strength of microwave irradiation is less demanded than that in the solid effect. In practice, the correct EPR frequency separation is accomplished through random orientation of paramagnetic species with g-anisotropy. Since the "frequency" distance between the two electrons should be equal to the Larmor frequency of the targeted nucleus, cross-effect can only occur if the inhomogeneously broadened EPR lineshape has a linewidth broader than the nuclear Larmor frequency. Therefore, as this linewidth is proportional to external magnetic field B0, the overall DNP efficiency (or the enhancement of nuclear polarization) scales as B0−1. This remains true as long as the relaxation times remain constant. Usually going to higher field leads to longer nuclear relaxation times and this may partially compensate for the line broadening reduction. In practice, in a glassy sample, the probability of having two dipolarly coupled electrons separated by the Larmor frequency is very scarce. Nonetheless, this mechanism is so efficient that it can be experimentally observed alone or in addition to the solid-effect.
Magic angle spinning case
As in the static case, the MAS-DNP mechanism of cross effect is deeply modified due to the time dependent energy level. By taking a simple three spin system, it has been demonstrated that the cross-effect mechanism is different in the Static and MAS case. The cross effect is the result of very fast multi-step process involving EPR single quantum transition, electron dipolar anti-crossing and cross effect degeneracy conditions. In the most simple case the MAS-DNP mechanism can be explained by the combination of a single quantum transition followed by the cross-effect degeneracy condition, or by the electron-dipolar anti-crossing followed by the cross-effect degeneracy condition.
This in turn change dramatically the CE dependence over the static magnetic field which does not scale like B0−1 and makes it much more efficient than the solid effect.
Thermal mixing
Thermal mixing is an energy exchange phenomenon between the electron spin ensemble and the nuclear spin, which can be thought of as using multiple electron spins to provide hyper-nuclear polarization. Note that the electron spin ensemble acts as a whole because of stronger inter-electron interactions. The strong interactions lead to a homogeneously broadened EPR lineshape of the involved paramagnetic species. The linewidth is optimized for polarization transfer from electrons to nuclei, when it is close to the nuclear Larmor frequency. The optimization is related to an embedded three-spin (electron-electron-nucleus) process that mutually flips the coupled three spins under the energy conservation (mainly) of the Zeeman interactions. Due to the inhomogeneous component of the associated EPR lineshape, the DNP enhancement by this mechanism also scales as B0−1.
DNP-NMR enhancement curves
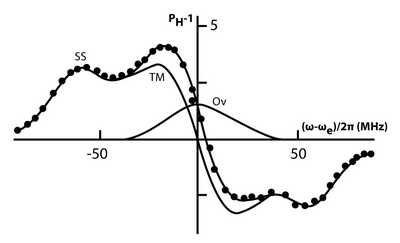
Many types of solid materials can exhibit more than one mechanism for DNP. Some examples are carbonaceous materials such bituminous coal and charcoal (wood or cellulose heated at high temperatures above their decomposition point which leaves a residual solid char). To separate out the mechanisms of DNP and to characterize the electron-nuclear interactions occurring in such solids a DNP enhancement curve can be made. A typical enhancement curve is obtained by measuring the maximum intensity of the NMR FID of the 1H nuclei, for example, in the presence of continuous microwave irradiation as a function of the microwave frequency offset.
Carbonaceous materials such as cellulose char contain large numbers of stable free electrons delocalized in large polycyclic aromatic hydrocarbons. Such electrons can give large polarization enhancements to nearby protons via proton-proton spin-diffusion if they are not so close together that the electron-nuclear dipolar interaction does not broaden the proton resonance beyond detection. For small isolated clusters, the free electrons are fixed and give rise to solid-state enhancements (SS). The maximal proton solid-state enhancement is observed at microwave offsets of ω ≈ ωe ± ωH, where ωe and ωH are the electron and nuclear Larmor frequencies, respectively. For larger and more densely concentrated aromatic clusters, the free electrons can undergo rapid electron exchange interactions. These electrons give rise to an Overhauser enhancement centered at a microwave offset of ωe – ωH = 0. The cellulose char also exhibits electrons undergoing thermal mixing effects (TM). While the enhancement curve reveals the types electron-nuclear spin interactions in a material, it is not quantitative and the relative abundance of the different types of nuclei cannot be determined directly from the curve.





























![{\displaystyle [p_{x},H]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ac4683d7b95f08cb67a9705027f1f3eb74b67e2)
![{\displaystyle [H,\operatorname {T} (a)]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c27d81bcad703e4df6dbf760d00b58c91237268f)











![{\displaystyle \operatorname {R} (z,dt)=\exp \left[-{\frac {i}{\hbar }}\left(xp_{y}-yp_{x}\right)dt\right]=\exp \left(-{\frac {i}{\hbar }}L_{z}dt\right)=1-{\frac {i}{\hbar }}L_{z}dt+\cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e706213a1d81d36483b133417102966271d9d16d)



![{\displaystyle {\begin{aligned}&\operatorname {R} (z,t+dt)=\operatorname {R} (z,t)\operatorname {R} (z,dt)\\[1.1ex]\Rightarrow {}&{\frac {d\operatorname {R} }{dt}}={\frac {\operatorname {R} (z,t+dt)-\operatorname {R} (z,t)}{dt}}=\operatorname {R} (z,t){\frac {\operatorname {R} (z,dt)-1}{dt}}=-{\frac {i}{\hbar }}L_{z}\operatorname {R} (z,t)\\[1.1ex]\Rightarrow {}&\operatorname {R} (z,t)=\exp \left(-{\frac {i}{\hbar }}\,t\,L_{z}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef6f72cb544ee1c3f63e21ec324269ce87655498)
![{\displaystyle [L_{z},H]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a428a66380deb52c3d77434ad3e02b8c1b8bda30)
![{\displaystyle [\operatorname {R} (z,t),H]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f98875d763eb69b9312d65f6807fff522837a6fd)




















