Gravitational potential

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Gravitational_potential

Plot of a two-dimensional slice of the gravitational potential in and around a uniform spherical body. The inflection points of the cross-section are at the surface of the body.

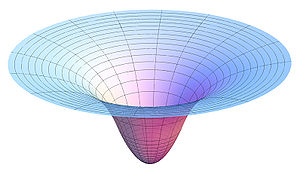
In classical mechanics, the gravitational potential at a location is equal to the work (energy transferred) per unit mass that would be needed to move an object to that location from a fixed reference location. It is analogous to the electric potential with mass playing the role of charge. The reference location, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance.

In mathematics, the gravitational potential is also known as the Newtonian potential and is fundamental in the study of potential theory. It may also be used for solving the electrostatic and magnetostatic fields generated by uniformly charged or polarized ellipsoidal bodies.

Potential energy

Main article: Gravitational potential energy

The gravitational potential (V) at a location is the gravitational potential energy (U) at that location per unit mass:

$${\displaystyle V=\frac{U}{m},}$$

where m is the mass of the object. Potential energy is equal (in magnitude, but negative) to the work done by the gravitational field moving a body to its given position in space from infinity. If the body has a mass of 1 kilogram, then the potential energy to be assigned to that body is equal to the gravitational potential. So the potential can be interpreted as the negative of the work done by the gravitational field moving a unit mass in from infinity.

In some situations, the equations can be simplified by assuming a field that is nearly independent of position. For instance, in a region close to the surface of the Earth, the gravitational acceleration, g, can be considered constant. In that case, the difference in potential energy from one height to another is, to a good approximation, linearly related to the difference in height:

$${\displaystyle \mathrm{\Delta }U\approx mg\mathrm{\Delta }h.}$$

Mathematical form

The gravitational potential V at a distance x from a point mass of mass M can be defined as the work W that needs to be done by an external agent to bring a unit mass in from infinity to that point:

$${\displaystyle V(\mathbf{x})=\frac{W}{m}=\frac{1}{m}{\int }_{\mathrm{\infty }}^x\mathbf{F}\cdot d\mathbf{x}=\frac{1}{m}{\int }_{\mathrm{\infty }}^x\frac{GmM}{x^2}dx=-\frac{GM}{x},}$$

where G is the gravitational constant, and F is the gravitational force. The product GM is the standard gravitational parameter and is often known to higher precision than G or M separately. The potential has units of energy per mass, e.g., J/kg in the MKS system. By convention, it is always negative where it is defined, and as x tends to infinity, it approaches zero.

The gravitational field, and thus the acceleration of a small body in the space around the massive object, is the negative gradient of the gravitational potential. Thus the negative of a negative gradient yields positive acceleration toward a massive object. Because the potential has no angular components, its gradient is

$${\displaystyle \mathbf{a}=-\frac{GM}{x^3}\mathbf{x}=-\frac{GM}{x^2}\hat{\mathbf{x}},}$$

where x is a vector of length x pointing from the point mass toward the small body and ${\displaystyle \hat{\mathbf{x}}}$ is a unit vector pointing from the point mass toward the small body. The magnitude of the acceleration therefore follows an inverse square law:

$${\displaystyle |\mathbf{a}|=\frac{GM}{x^2}.}$$

The potential associated with a mass distribution is the superposition of the potentials of point masses. If the mass distribution is a finite collection of point masses, and if the point masses are located at the points x₁, ..., x_n and have masses m₁, ..., m_n, then the potential of the distribution at the point x is

$${\displaystyle V(\mathbf{x})=\sum _{i=1}^n-\frac{G{m}_i}{|\mathbf{x}-{\mathbf{x}}_i|}.}$$

Points x and r, with r contained in the distributed mass (gray) and differential mass dm(r) located at the point r.

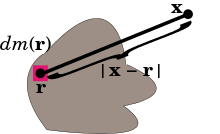
If the mass distribution is given as a mass measure dm on three-dimensional Euclidean space R³, then the potential is the convolution of −G/|r| with dm. In good cases this equals the integral

$${\displaystyle V(\mathbf{x})=-{\int }_{{\mathbb{R}}^3}\frac{G}{|\mathbf{x}-\mathbf{r}|}dm(\mathbf{r}),}$$

where |x − r| is the distance between the points x and r. If there is a function ρ(r) representing the density of the distribution at r, so that dm(r) = ρ(r) dv(r), where dv(r) is the Euclidean volume element, then the gravitational potential is the volume integral

$${\displaystyle V(\mathbf{x})=-{\int }_{{\mathbb{R}}^3}\frac{G}{|\mathbf{x}-\mathbf{r}|}\rho (\mathbf{r})dv(\mathbf{r}).}$$

If V is a potential function coming from a continuous mass distribution ρ(r), then ρ can be recovered using the Laplace operator, Δ:

$${\displaystyle \rho (\mathbf{x})=\frac{1}{4\pi G}\mathrm{\Delta }V(\mathbf{x}).}$$

This holds pointwise whenever ρ is continuous and is zero outside of a bounded set. In general, the mass measure dm can be recovered in the same way if the Laplace operator is taken in the sense of distributions. As a consequence, the gravitational potential satisfies Poisson's equation. See also Green's function for the three-variable Laplace equation and Newtonian potential.

The integral may be expressed in terms of known transcendental functions for all ellipsoidal shapes, including the symmetrical and degenerate ones. These include the sphere, where the three semi axes are equal; the oblate (see reference ellipsoid) and prolate spheroids, where two semi axes are equal; the degenerate ones where one semi axes is infinite (the elliptical and circular cylinder) and the unbounded sheet where two semi axes are infinite. All these shapes are widely used in the applications of the gravitational potential integral (apart from the constant G, with 𝜌 being a constant charge density) to electromagnetism.

Spherical symmetry

A spherically symmetric mass distribution behaves to an observer completely outside the distribution as though all of the mass was concentrated at the center, and thus effectively as a point mass, by the shell theorem. On the surface of the earth, the acceleration is given by so-called standard gravity g, approximately 9.8 m/s², although this value varies slightly with latitude and altitude. The magnitude of the acceleration is a little larger at the poles than at the equator because Earth is an oblate spheroid.

Within a spherically symmetric mass distribution, it is possible to solve Poisson's equation in spherical coordinates. Within a uniform spherical body of radius R, density ρ, and mass m, the gravitational force g inside the sphere varies linearly with distance r from the center, giving the gravitational potential inside the sphere, which is

$${\displaystyle V(r)=\frac{2}{3}\pi G\rho \left[r^2-3R^2\right]=\frac{Gm}{2R^3}\left[r^2-3R^2\right],r\le R,}$$

which differentiably connects to the potential function for the outside of the sphere (see the figure at the top).

General relativity

See also: Gravitational acceleration § General relativity, and Gravitational field § General relativity

In general relativity, the gravitational potential is replaced by the metric tensor. When the gravitational field is weak and the sources are moving very slowly compared to light-speed, general relativity reduces to Newtonian gravity, and the metric tensor can be expanded in terms of the gravitational potential.

Multipole expansion

Main articles: Spherical multipole moments and Multipole expansion

The potential at a point x is given by

$${\displaystyle V(\mathbf{x})=-{\int }_{{\mathbb{R}}^3}\frac{G}{|\mathbf{x}-\mathbf{r}|}dm(\mathbf{r}).}$$

Illustration of a mass distribution (grey) with center of mass as the origin of vectors x and r and the point at which the potential is being computed at the head of vector x.

The potential can be expanded in a series of Legendre polynomials. Represent the points x and r as position vectors relative to the center of mass. The denominator in the integral is expressed as the square root of the square to give

$${\displaystyle \begin{array}{rl}V(\mathbf{x})& =-{\int }_{{\mathbb{R}}^3}\frac{G}{\sqrt{|\mathbf{x}{|}^2-2\mathbf{x}\cdot \mathbf{r}+|\mathbf{r}{|}^2}}dm(\mathbf{r})\\ & =-\frac{1}{|\mathbf{x}|}{\int }_{{\mathbb{R}}^3}\frac{G}{\sqrt{1-2\frac{r}{|\mathbf{x}|}\cos \theta +{\left(\frac{r}{|\mathbf{x}|}\right)}^2}}dm(\mathbf{r})\end{array}}$$

where, in the last integral, r = |r| and θ is the angle between x and r.

(See "mathematical form".) The integrand can be expanded as a Taylor series in Z = r/|x|, by explicit calculation of the coefficients. A less laborious way of achieving the same result is by using the generalized binomial theorem. The resulting series is the generating function for the Legendre polynomials:

$${\displaystyle {\left(1-2XZ+Z^2\right)}^{-\frac{1}{2}}=\sum _{n=0}^{\mathrm{\infty }}{Z}^n{P}_n(X)}$$

valid for |X| ≤ 1 and |Z| < 1. The coefficients P_n are the Legendre polynomials of degree n. Therefore, the Taylor coefficients of the integrand are given by the Legendre polynomials in X = cos θ. So the potential can be expanded in a series that is convergent for positions x such that r < |x| for all mass elements of the system (i.e., outside a sphere, centered at the center of mass, that encloses the system):

$${\displaystyle \begin{array}{rl}V(\mathbf{x})& =-\frac{G}{|\mathbf{x}|}\int \sum _{n=0}^{\mathrm{\infty }}{\left(\frac{r}{|\mathbf{x}|}\right)}^n{P}_n(\cos \theta )dm(\mathbf{r})\\ & =-\frac{G}{|\mathbf{x}|}\int \left(1+\left(\frac{r}{|\mathbf{x}|}\right)\cos \theta +{\left(\frac{r}{|\mathbf{x}|}\right)}^2\frac{3{\cos }^2\theta -1}{2}+\cdots \right)dm(\mathbf{r})\end{array}}$$

The integral $\int r\cos (\theta )dm$ is the component of the center of mass in the x direction; this vanishes because the vector x emanates from the center of mass. So, bringing the integral under the sign of the summation gives

$${\displaystyle V(\mathbf{x})=-\frac{GM}{|\mathbf{x}|}-\frac{G}{|\mathbf{x}|}\int {\left(\frac{r}{|\mathbf{x}|}\right)}^2\frac{3{\cos }^2\theta -1}{2}dm(\mathbf{r})+\cdots }$$

This shows that elongation of the body causes a lower potential in the direction of elongation, and a higher potential in perpendicular directions, compared to the potential due to a spherical mass, if we compare cases with the same distance to the center of mass. (If we compare cases with the same distance to the surface, the opposite is true.)

Numerical values

The absolute value of gravitational potential at a number of locations with regards to the gravitation from the Earth, the Sun, and the Milky Way is given in the following table; i.e. an object at Earth's surface would need 60 MJ/kg to "leave" Earth's gravity field, another 900 MJ/kg to also leave the Sun's gravity field and more than 130 GJ/kg to leave the gravity field of the Milky Way. The potential is half the square of the escape velocity.

Location	with respect to
	Earth	Sun	Milky Way
Earth's surface	60 MJ/kg	900 MJ/kg	≥ 130 GJ/kg
LEO	57 MJ/kg	900 MJ/kg	≥ 130 GJ/kg
Voyager 1 (17,000 million km from Earth)	23 J/kg	8 MJ/kg	≥ 130 GJ/kg
0.1 light-year from Earth	0.4 J/kg	140 kJ/kg	≥ 130 GJ/kg

Compare the gravity at these locations.

Nuclear reaction

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Nuclear_reaction

In this symbolic representing of a nuclear reaction, lithium-6 (⁶
₃Li
) and deuterium (²
₁H
) react to form the highly excited intermediate nucleus ⁸
₄Be
which then decays immediately into two alpha particles of helium-4 (⁴
₂He
). Protons are symbolically represented by red spheres, and neutrons by blue spheres.

In nuclear physics and nuclear chemistry, a nuclear reaction is a process in which two nuclei, or a nucleus and an external subatomic particle, collide to produce one or more new nuclides. Thus, a nuclear reaction must cause a transformation of at least one nuclide to another. If a nucleus interacts with another nucleus or particle and they then separate without changing the nature of any nuclide, the process is simply referred to as a type of nuclear scattering, rather than a nuclear reaction.

In principle, a reaction can involve more than two particles colliding, but because the probability of three or more nuclei to meet at the same time at the same place is much less than for two nuclei, such an event is exceptionally rare (see triple alpha process for an example very close to a three-body nuclear reaction). The term "nuclear reaction" may refer either to a change in a nuclide induced by collision with another particle or to a spontaneous change of a nuclide without collision.

Natural nuclear reactions occur in the interaction between cosmic rays and matter, and nuclear reactions can be employed artificially to obtain nuclear energy, at an adjustable rate, on-demand. Nuclear chain reactions in fissionable materials produce induced nuclear fission. Various nuclear fusion reactions of light elements power the energy production of the Sun and stars.

History

In 1919, Ernest Rutherford was able to accomplish transmutation of nitrogen into oxygen at the University of Manchester, using alpha particles directed at nitrogen ¹⁴N + α → ¹⁷O + p.  This was the first observation of an induced nuclear reaction, that is, a reaction in which particles from one decay are used to transform another atomic nucleus. Eventually, in 1932 at Cambridge University, a fully artificial nuclear reaction and nuclear transmutation was achieved by Rutherford's colleagues John Cockcroft and Ernest Walton, who used artificially accelerated protons against lithium-7, to split the nucleus into two alpha particles. The feat was popularly known as "splitting the atom", although it was not the modern nuclear fission reaction later (in 1938) discovered in heavy elements by the German scientists Otto Hahn, Lise Meitner, and Fritz Strassmann.

Nuclear reaction equations

Nuclear reactions may be shown in a form similar to chemical equations, for which invariant mass must balance for each side of the equation, and in which transformations of particles must follow certain conservation laws, such as conservation of charge and baryon number (total atomic mass number). An example of this notation follows:

6 3Li

+

2 1H

→

4 2He

+

?.

To balance the equation above for mass, charge and mass number, the second nucleus to the right must have atomic number 2 and mass number 4; it is therefore also helium-4. The complete equation therefore reads:

6 3Li

+

2 1H

→

4 2He

+

4 2He .

or more simply:

6 3Li

+

2 1H

→

2 4 2He .

Instead of using the full equations in the style above, in many situations a compact notation is used to describe nuclear reactions. This style of the form A(b,c)D is equivalent to A + b producing c + D. Common light particles are often abbreviated in this shorthand, typically p for proton, n for neutron, d for deuteron, α representing an alpha particle or helium-4, β for beta particle or electron, γ for gamma photon, etc. The reaction above would be written as ⁶Li(d,α)α.

Energy conservation

Kinetic energy may be released during the course of a reaction (exothermic reaction) or kinetic energy may have to be supplied for the reaction to take place (endothermic reaction). This can be calculated by reference to a table of very accurate particle rest masses, as follows: according to the reference tables, the ⁶
₃Li
nucleus has a standard atomic weight of 6.015 atomic mass units (abbreviated u), the deuterium has 2.014 u, and the helium-4 nucleus has 4.0026 u. Thus:

• the sum of the rest mass of the individual nuclei = 6.015 + 2.014 = 8.029 u;
• the total rest mass on the two helium-nuclei = 2 × 4.0026 = 8.0052 u;
• missing rest mass = 8.029 – 8.0052 = 0.0238 atomic mass units.

In a nuclear reaction, the total (relativistic) energy is conserved. The "missing" rest mass must therefore reappear as kinetic energy released in the reaction; its source is the nuclear binding energy. Using Einstein's mass-energy equivalence formula E = mc², the amount of energy released can be determined. We first need the energy equivalent of one atomic mass unit:

1 u c² = (1.66054 × 10⁻²⁷ kg) × (2.99792 × 10⁸ m/s)² 

= 1.49242 × 10⁻¹⁰ kg (m/s)² = 1.49242 × 10⁻¹⁰ J (joule) × (1 MeV / 1.60218 × 10⁻¹³ J)

= 931.49 MeV,

so 1 u c² = 931.49 MeV.

Hence, the energy released is 0.0238 × 931 MeV = 22.2 MeV.

Expressed differently: the mass is reduced by 0.3%, corresponding to 0.3% of 90 PJ/kg is 270 TJ/kg.

This is a large amount of energy for a nuclear reaction; the amount is so high because the binding energy per nucleon of the helium-4 nucleus is unusually high because the He-4 nucleus is "doubly magic". (The He-4 nucleus is unusually stable and tightly bound for the same reason that the helium atom is inert: each pair of protons and neutrons in He-4 occupies a filled 1s nuclear orbital in the same way that the pair of electrons in the helium atom occupy a filled 1s electron orbital). Consequently, alpha particles appear frequently on the right-hand side of nuclear reactions.

The energy released in a nuclear reaction can appear mainly in one of three ways:

• kinetic energy of the product particles (fraction of the kinetic energy of the charged nuclear reaction products can be directly converted into electrostatic energy);
• emission of very high energy photons, called gamma rays;
• some energy may remain in the nucleus, as a metastable energy level.

When the product nucleus is metastable, this is indicated by placing an asterisk ("*") next to its atomic number. This energy is eventually released through nuclear decay.

A small amount of energy may also emerge in the form of X-rays. Generally, the product nucleus has a different atomic number, and thus the configuration of its electron shells is wrong. As the electrons rearrange themselves and drop to lower energy levels, internal transition X-rays (X-rays with precisely defined emission lines) may be emitted.

Q-value and energy balance

In writing down the reaction equation, in a way analogous to a chemical equation, one may, in addition, give the reaction energy on the right side:

Target nucleus + projectile → Final nucleus + ejectile + Q.

For the particular case discussed above, the reaction energy has already been calculated as Q = 22.2 MeV. Hence:

6 3Li

+

2 1H

→

2 4 2He

+

22.2 MeV.

The reaction energy (the "Q-value") is positive for exothermal reactions and negative for endothermal reactions, opposite to the similar expression in chemistry. On the one hand, it is the difference between the sums of kinetic energies on the final side and on the initial side. But on the other hand, it is also the difference between the nuclear rest masses on the initial side and on the final side (in this way, we have calculated the Q-value above).

Reaction rates

If the reaction equation is balanced, that does not mean that the reaction really occurs. The rate at which reactions occur depends on the energy and the flux of the incident particles, and the reaction cross section. An example of a large repository of reaction rates is the REACLIB database, as maintained by the Joint Institute for Nuclear Astrophysics.

Charged vs. uncharged particles

In the initial collision which begins the reaction, the particles must approach closely enough so that the short-range strong force can affect them. As most common nuclear particles are positively charged, this means they must overcome considerable electrostatic repulsion before the reaction can begin. Even if the target nucleus is part of a neutral atom, the other particle must penetrate well beyond the electron cloud and closely approach the nucleus, which is positively charged. Thus, such particles must be first accelerated to high energy, for example by:

• particle accelerators;
• nuclear decay (alpha particles are the main type of interest here since beta and gamma rays are rarely involved in nuclear reactions);
• very high temperatures, on the order of millions of degrees, producing thermonuclear reactions;
• cosmic rays.

Also, since the force of repulsion is proportional to the product of the two charges, reactions between heavy nuclei are rarer, and require higher initiating energy, than those between a heavy and light nucleus; while reactions between two light nuclei are the most common ones.

Neutrons, on the other hand, have no electric charge to cause repulsion, and are able to initiate a nuclear reaction at very low energies. In fact, at extremely low particle energies (corresponding, say, to thermal equilibrium at room temperature), the neutron's de Broglie wavelength is greatly increased, possibly greatly increasing its capture cross-section, at energies close to resonances of the nuclei involved. Thus low-energy neutrons may be even more reactive than high-energy neutrons.

Notable types

While the number of possible nuclear reactions is immense, there are several types that are more common, or otherwise notable. Some examples include:

• Fusion reactions — two light nuclei join to form a heavier one, with additional particles (usually protons or neutrons) emitted subsequently.
• Spallation — a nucleus is hit by a particle with sufficient energy and momentum to knock out several small fragments or smash it into many fragments.
• Induced gamma emission belongs to a class in which only photons were involved in creating and destroying states of nuclear excitation.
• Alpha decay — Though driven by the same underlying forces as spontaneous fission, α decay is usually considered to be separate from the latter. The often-quoted idea that "nuclear reactions" are confined to induced processes is incorrect. "Radioactive decays" are a subgroup of "nuclear reactions" that are spontaneous rather than induced. For example, so-called "hot alpha particles" with unusually high energies may actually be produced in induced ternary fission, which is an induced nuclear reaction (contrasting with spontaneous fission). Such alphas occur from spontaneous ternary fission as well.
• Fission reactions — a very heavy nucleus, after absorbing additional light particles (usually neutrons), splits into two or sometimes three pieces. This is an induced nuclear reaction. Spontaneous fission, which occurs without assistance of a neutron, is usually not considered a nuclear reaction. At most, it is not an induced nuclear reaction.

Direct reactions

An intermediate energy projectile transfers energy or picks up or loses nucleons to the nucleus in a single quick (10⁻²¹ second) event. Energy and momentum transfer are relatively small. These are particularly useful in experimental nuclear physics, because the reaction mechanisms are often simple enough to calculate with sufficient accuracy to probe the structure of the target nucleus.

Inelastic scattering

Main article: Inelastic scattering

Only energy and momentum are transferred.

• (p,p') tests differences between nuclear states.
• (α,α') measures nuclear surface shapes and sizes. Since α particles that hit the nucleus react more violently, elastic and shallow inelastic α scattering are sensitive to the shapes and sizes of the targets, like light scattered from a small black object.
• (e,e') is useful for probing the interior structure. Since electrons interact less strongly than do protons and neutrons, they reach to the centers of the targets and their wave functions are less distorted by passing through the nucleus.

Charge-exchange reactions

Energy and charge are transferred between projectile and target. Some examples of this kind of reactions are:

• (p,n)
• (³He,t)

Nucleon transfer reactions

Usually at moderately low energy, one or more nucleons are transferred between the projectile and target. These are useful in studying outer shell structure of nuclei. Transfer reactions can occur, from the projectile to the target; stripping reactions, or from the target to the projectile; pick-up reactions.

• (α,n) and (α,p) reactions. Some of the earliest nuclear reactions studied involved an alpha particle produced by alpha decay, knocking a nucleon from a target nucleus.
• (d,n) and (d,p) reactions. A deuteron beam impinges on a target; the target nuclei absorb either the neutron or proton from the deuteron. The deuteron is so loosely bound that this is almost the same as proton or neutron capture. A compound nucleus may be formed, leading to additional neutrons being emitted more slowly. (d,n) reactions are used to generate energetic neutrons.
• The strangeness exchange reaction (K, π) has been used to study hypernuclei.
• The reaction ¹⁴N(α,p)¹⁷O performed by Rutherford in 1917 (reported 1919), is generally regarded as the first nuclear transmutation experiment.

Reactions with neutrons

	→ T	→ 7Li	→ 14C
(n,α)	6Li + n → T + α	10B + n → 7Li + α	17O + n → 14C + α	21Ne + n → 18O + α	37Ar + n → 34S + α
(n,p)	3He + n → T + p	7Be + n → 7Li + p	14N + n → 14C + p	22Na + n → 22Ne + p
(n,γ)	2H + n → T + γ		13C + n → 14C + γ

Reactions with neutrons are important in nuclear reactors and nuclear weapons. While the best-known neutron reactions are neutron scattering, neutron capture, and nuclear fission, for some light nuclei (especially odd-odd nuclei) the most probable reaction with a thermal neutron is a transfer reaction:

Some reactions are only possible with fast neutrons:

• (n,2n) reactions produce small amounts of protactinium-231 and uranium-232 in the thorium cycle which is otherwise relatively free of highly radioactive actinide products.
• ⁹Be + n → 2α + 2n can contribute some additional neutrons in the beryllium neutron reflector of a nuclear weapon.
• ⁷Li + n → T + α + n unexpectedly contributed additional yield in the Bravo, Romeo and Yankee shots of Operation Castle, the three highest-yield nuclear tests conducted by the U.S.

Compound nuclear reactions

Either a low-energy projectile is absorbed or a higher energy particle transfers energy to the nucleus, leaving it with too much energy to be fully bound together. On a time scale of about 10⁻¹⁹ seconds, particles, usually neutrons, are "boiled" off. That is, it remains together until enough energy happens to be concentrated in one neutron to escape the mutual attraction. The excited quasi-bound nucleus is called a compound nucleus.

• Low energy (e, e' xn), (γ, xn) (the xn indicating one or more neutrons), where the gamma or virtual gamma energy is near the giant dipole resonance. These increase the need for radiation shielding around electron accelerators.

Further information: Spallation § Nuclear spallation