RAID

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/RAID

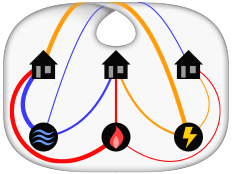
RAID (/reɪd/; redundant array of inexpensive disks or redundant array of independent disks) is a data storage virtualization technology that combines multiple physical data storage components into one or more logical units for the purposes of data redundancy, performance improvement, or both. This is in contrast to the previous concept of highly reliable mainframe disk drives known as single large expensive disk (SLED)

Data is distributed across the drives in one of several ways, referred to as RAID levels, depending on the required level of redundancy and performance. The different schemes, or data distribution layouts, are named by the word "RAID" followed by a number, for example RAID 0 or RAID 1. Each scheme, or RAID level, provides a different balance among the key goals: reliability, availability, performance, and capacity. RAID levels greater than RAID 0 provide protection against unrecoverable sector read errors, as well as against failures of whole physical drives.

History

The term "RAID" was invented by David Patterson, Garth Gibson, and Randy Katz at the University of California, Berkeley in 1987. In their June 1988 paper "A Case for Redundant Arrays of Inexpensive Disks (RAID)", presented at the SIGMOD Conference, they argued that the top-performing mainframe disk drives of the time could be beaten on performance by an array of the inexpensive drives that had been developed for the growing personal computer market. Although failures would rise in proportion to the number of drives, by configuring for redundancy, the reliability of an array could far exceed that of any large single drive.

Although not yet using that terminology, the technologies of the five levels of RAID named in the June 1988 paper were used in various products prior to the paper's publication, including the following:

• Mirroring (RAID 1) was well established in the 1970s including, for example, Tandem NonStop Systems.
• In 1977, Norman Ken Ouchi at IBM filed a patent disclosing what was subsequently named RAID 4.
• Around 1983, DEC began shipping subsystem mirrored RA8X disk drives (now known as RAID 1) as part of its HSC50 subsystem.
• In 1986, Clark et al. at IBM filed a patent disclosing what was subsequently named RAID 5.
• Around 1988, the Thinking Machines' DataVault used error correction codes (now known as RAID 2) in an array of disk drives. A similar approach was used in the early 1960s on the IBM 353.

Industry manufacturers later redefined the RAID acronym to stand for "redundant array of independent disks".

Overview

Many RAID levels employ an error protection scheme called "parity", a widely used method in information technology to provide fault tolerance in a given set of data. Most use simple XOR, but RAID 6 uses two separate parities based respectively on addition and multiplication in a particular Galois field or Reed–Solomon error correction.

RAID can also provide data security with solid-state drives (SSDs) without the expense of an all-SSD system. For example, a fast SSD can be mirrored with a mechanical drive. For this configuration to provide a significant speed advantage, an appropriate controller is needed that uses the fast SSD for all read operations. Adaptec calls this "hybrid RAID".

Standard levels

Main article: Standard RAID levels

Storage servers with 24 hard disk drives each and built-in hardware RAID controllers supporting various RAID levels

Originally, there were five standard levels of RAID, but many variations have evolved, including several nested levels and many non-standard levels (mostly proprietary). RAID levels and their associated data formats are standardized by the Storage Networking Industry Association (SNIA) in the Common RAID Disk Drive Format (DDF) standard:

• RAID 0 consists of block-level striping, but no mirroring or parity. Assuming n fully-used drives of equal capacity, the capacity of a RAID 0 volume matches that of a spanned volume: the total of the n drives' capacities. However, because striping distributes the contents of each file across all drives, the failure of any drive renders the entire RAID 0 volume inaccessible. Typically, all data is lost, and files cannot be recovered without a backup copy.

By contrast, a spanned volume, which stores files sequentially, loses data stored on the failed drive but preserves data stored on the remaining drives. However, recovering the files after drive failure can be challenging and often depends on the specifics of the filesystem. Regardless, files that span onto or off a failed drive will be permanently lost.

On the other hand, the benefit of RAID 0 is that the throughput of read and write operations to any file is multiplied by the number of drives because, unlike spanned volumes, reads and writes are performed concurrently. The cost is increased vulnerability to drive failures—since any drive in a RAID 0 setup failing causes the entire volume to be lost, the average failure rate of the volume rises with the number of attached drives. This makes RAID 0 a poor choice for scenarios requiring data reliability or fault tolerance.

• RAID 1 consists of data mirroring, without parity or striping. Data is written identically to two or more drives, thereby producing a "mirrored set" of drives. Thus, any read request can be serviced by any drive in the set. If a request is broadcast to every drive in the set, it can be serviced by the drive that accesses the data first (depending on its seek time and rotational latency), improving performance. Sustained read throughput, if the controller or software is optimized for it, approaches the sum of throughputs of every drive in the set, just as for RAID 0. Actual read throughput of most RAID 1 implementations is slower than the fastest drive. Write throughput is always slower because every drive must be updated, and the slowest drive limits the write performance. The array continues to operate as long as at least one drive is functioning.
• RAID 2 consists of bit-level striping with dedicated Hamming-code parity. All disk spindle rotation is synchronized and data is striped such that each sequential bit is on a different drive. Hamming-code parity is calculated across corresponding bits and stored on at least one parity drive. This level is of historical significance only; although it was used on some early machines (for example, the Thinking Machines CM-2), as of 2014 it is not used by any commercially available system.
• RAID 3 consists of byte-level striping with dedicated parity. All disk spindle rotation is synchronized and data is striped such that each sequential byte is on a different drive. Parity is calculated across corresponding bytes and stored on a dedicated parity drive. Although implementations exist, RAID 3 is not commonly used in practice.
• RAID 4 consists of block-level striping with dedicated parity. This level was previously used by NetApp, but has now been largely replaced by a proprietary implementation of RAID 4 with two parity disks, called RAID-DP. The main advantage of RAID 4 over RAID 2 and 3 is I/O parallelism: in RAID 2 and 3, a single read I/O operation requires reading the whole group of data drives, while in RAID 4 one I/O read operation does not have to spread across all data drives. As a result, more I/O operations can be executed in parallel, improving the performance of small transfers.
• RAID 5 consists of block-level striping with distributed parity. Unlike RAID 4, parity information is distributed among the drives, requiring all drives but one to be present to operate. Upon failure of a single drive, subsequent reads can be calculated from the distributed parity such that no data is lost. RAID 5 requires at least three disks. Like all single-parity concepts, large RAID 5 implementations are susceptible to system failures because of trends regarding array rebuild time and the chance of drive failure during rebuild (see "Increasing rebuild time and failure probability" section, below). Rebuilding an array requires reading all data from all disks, opening a chance for a second drive failure and the loss of the entire array.
• RAID 6 consists of block-level striping with double distributed parity. Double parity provides fault tolerance up to two failed drives. This makes larger RAID groups more practical, especially for high-availability systems, as large-capacity drives take longer to restore. RAID 6 requires a minimum of four disks. As with RAID 5, a single drive failure results in reduced performance of the entire array until the failed drive has been replaced. With a RAID 6 array, using drives from multiple sources and manufacturers, it is possible to mitigate most of the problems associated with RAID 5. The larger the drive capacities and the larger the array size, the more important it becomes to choose RAID 6 instead of RAID 5. RAID 10 also minimizes these problems.

Nested (hybrid) RAID

Main article: Nested RAID levels

In what was originally termed hybrid RAID, many storage controllers allow RAID levels to be nested. The elements of a RAID may be either individual drives or arrays themselves. Arrays are rarely nested more than one level deep.

The final array is known as the top array. When the top array is RAID 0 (such as in RAID 1+0 and RAID 5+0), most vendors omit the "+" (yielding RAID 10 and RAID 50, respectively).

• RAID 0+1: creates two stripes and mirrors them. If a single drive failure occurs then one of the mirrors has failed, at this point it is running effectively as RAID 0 with no redundancy. Significantly higher risk is introduced during a rebuild than RAID 1+0 as all the data from all the drives in the remaining stripe has to be read rather than just from one drive, increasing the chance of an unrecoverable read error (URE) and significantly extending the rebuild window.
• RAID 1+0: (see: RAID 10) creates a striped set from a series of mirrored drives. The array can sustain multiple drive losses so long as no mirror loses all its drives.
• JBOD RAID N+N: With JBOD (just a bunch of disks), it is possible to concatenate disks, but also volumes such as RAID sets. With larger drive capacities, write delay and rebuilding time increase dramatically (especially, as described above, with RAID 5 and RAID 6). By splitting a larger RAID N set into smaller subsets and concatenating them with linear JBOD, write and rebuilding time will be reduced. If a hardware RAID controller is not capable of nesting linear JBOD with RAID N, then linear JBOD can be achieved with OS-level software RAID in combination with separate RAID N subset volumes created within one, or more, hardware RAID controller(s). Besides a drastic speed increase, this also provides a substantial advantage: the possibility to start a linear JBOD with a small set of disks and to be able to expand the total set with disks of different size, later on (in time, disks of bigger size become available on the market). There is another advantage in the form of disaster recovery (if a RAID N subset happens to fail, then the data on the other RAID N subsets is not lost, reducing restore time). 

Non-standard levels

Main article: Non-standard RAID levels

Many configurations other than the basic numbered RAID levels are possible, and many companies, organizations, and groups have created their own non-standard configurations, in many cases designed to meet the specialized needs of a small niche group. Such configurations include the following:

• Linux MD RAID 10 provides a general RAID driver that in its "near" layout defaults to a standard RAID 1 with two drives, and a standard RAID 1+0 with four drives; however, it can include any number of drives, including odd numbers. With its "far" layout, MD RAID 10 can run both striped and mirrored, even with only two drives in f2 layout; this runs mirroring with striped reads, giving the read performance of RAID 0. Regular RAID 1, as provided by Linux software RAID, does not stripe reads, but can perform reads in parallel.
• Hadoop has a RAID system that generates a parity file by xor-ing a stripe of blocks in a single HDFS file.
• BeeGFS, the parallel file system, has internal striping (comparable to file-based RAID0) and replication (comparable to file-based RAID10) options to aggregate throughput and capacity of multiple servers and is typically based on top of an underlying RAID to make disk failures transparent.
• Declustered RAID scatters dual (or more) copies of the data across all disks (possibly hundreds) in a storage subsystem, while holding back enough spare capacity to allow for a few disks to fail. The scattering is based on algorithms which give the appearance of arbitrariness. When one or more disks fail the missing copies are rebuilt into that spare capacity, again arbitrarily. Because the rebuild is done from and to all the remaining disks, it operates much faster than with traditional RAID, reducing the overall impact on clients of the storage system.

Implementations

The distribution of data across multiple drives can be managed either by dedicated computer hardware or by software. A software solution may be part of the operating system, part of the firmware and drivers supplied with a standard drive controller (so-called "hardware-assisted software RAID"), or it may reside entirely within the hardware RAID controller.

Hardware-based

Main article: RAID controller

Hardware RAID controllers can be configured through card BIOS or Option ROM before an operating system is booted, and after the operating system is booted, proprietary configuration utilities are available from the manufacturer of each controller. Unlike the network interface controllers for Ethernet, which can usually be configured and serviced entirely through the common operating system paradigms like ifconfig in Unix, without a need for any third-party tools, each manufacturer of each RAID controller usually provides their own proprietary software tooling for each operating system that they deem to support, ensuring a vendor lock-in, and contributing to reliability issues.

For example, in FreeBSD, in order to access the configuration of Adaptec RAID controllers, users are required to enable Linux compatibility layer, and use the Linux tooling from Adaptec, potentially compromising the stability, reliability and security of their setup, especially when taking the long-term view.

Some other operating systems have implemented their own generic frameworks for interfacing with any RAID controller, and provide tools for monitoring RAID volume status, as well as facilitation of drive identification through LED blinking, alarm management and hot spare disk designations from within the operating system without having to reboot into card BIOS. For example, this was the approach taken by OpenBSD in 2005 with its bio(4) pseudo-device and the bioctl utility, which provide volume status, and allow LED/alarm/hotspare control, as well as the sensors (including the drive sensor) for health monitoring; this approach has subsequently been adopted and extended by NetBSD in 2007 as well.

Software-based

Software RAID implementations are provided by many modern operating systems. Software RAID can be implemented as:

• A layer that abstracts multiple devices, thereby providing a single virtual device (such as Linux kernel's md and OpenBSD's softraid)
• A more generic logical volume manager (provided with most server-class operating systems such as Veritas or LVM)
• A component of the file system (such as ZFS, Spectrum Scale or Btrfs)
• A layer that sits above any file system and provides parity protection to user data (such as RAID-F)

Some advanced file systems are designed to organize data across multiple storage devices directly, without needing the help of a third-party logical volume manager:

• ZFS supports the equivalents of RAID 0, RAID 1, RAID 5 (RAID-Z1) single-parity, RAID 6 (RAID-Z2) double-parity, and a triple-parity version (RAID-Z3) also referred to as RAID 7. As it always stripes over top-level vdevs, it supports equivalents of the 1+0, 5+0, and 6+0 nested RAID levels (as well as striped triple-parity sets) but not other nested combinations. ZFS is the native file system on Solaris and illumos, and is also available on FreeBSD and Linux. Open-source ZFS implementations are actively developed under the OpenZFS umbrella project.
• Spectrum Scale, initially developed by IBM for media streaming and scalable analytics, supports declustered RAID protection schemes up to n+3. A particularity is the dynamic rebuilding priority which runs with low impact in the background until a data chunk hits n+0 redundancy, in which case this chunk is quickly rebuilt to at least n+1. On top, Spectrum Scale supports metro-distance RAID 1.
• Btrfs supports RAID 0, RAID 1 and RAID 10 (RAID 5 and 6 are under development).
• XFS was originally designed to provide an integrated volume manager that supports concatenating, mirroring and striping of multiple physical storage devices. However, the implementation of XFS in Linux kernel lacks the integrated volume manager.

Many operating systems provide RAID implementations, including the following:

• Hewlett-Packard's OpenVMS operating system supports RAID 1. The mirrored disks, called a "shadow set", can be in different locations to assist in disaster recovery.
• Apple's macOS and macOS Server natively support RAID 0, RAID 1, and RAID 1+0, which can be created with Disk Utility or its command-line interface, while RAID 4 and RAID 5 can only be created using the third-party software SoftRAID by OWC, with the driver for SoftRAID access natively included since macOS 13.3.
• FreeBSD supports RAID 0, RAID 1, RAID 3, and RAID 5, and all nestings via GEOM modules and ccd.
• Linux's md supports RAID 0, RAID 1, RAID 4, RAID 5, RAID 6, and all nestings. Certain reshaping/resizing/expanding operations are also supported.
• Microsoft Windows supports RAID 0, RAID 1, and RAID 5 using various software implementations. Logical Disk Manager, introduced with Windows 2000, allows for the creation of RAID 0, RAID 1, and RAID 5 volumes by using dynamic disks, but this was limited only to professional and server editions of Windows until the release of Windows 8. Windows XP can be modified to unlock support for RAID 0, 1, and 5. Windows 8 and Windows Server 2012 introduced a RAID-like feature known as Storage Spaces, which also allows users to specify mirroring, parity, or no redundancy on a folder-by-folder basis. These options are similar to RAID 1 and RAID 5, but are implemented at a higher abstraction level.
• NetBSD supports RAID 0, 1, 4, and 5 via its software implementation, named RAIDframe.
• OpenBSD supports RAID 0, 1 and 5 via its software implementation, named softraid.

If a boot drive fails, the system has to be sophisticated enough to be able to boot from the remaining drive or drives. For instance, consider a computer whose disk is configured as RAID 1 (mirrored drives); if the first drive in the array fails, then a first-stage boot loader might not be sophisticated enough to attempt loading the second-stage boot loader from the second drive as a fallback. The second-stage boot loader for FreeBSD is capable of loading a kernel from such an array.

Firmware- and driver-based

See also: MD RAID external metadata

A SATA 3.0 controller that provides RAID functionality through proprietary firmware and drivers

Software-implemented RAID is not always compatible with the system's boot process, and it is generally impractical for desktop versions of Windows. However, hardware RAID controllers are expensive and proprietary. To fill this gap, inexpensive "RAID controllers" were introduced that do not contain a dedicated RAID controller chip, but simply a standard drive controller chip, or the chipset built-in RAID function, with proprietary firmware and drivers. During early bootup, the RAID is implemented by the firmware and, once the operating system has been more completely loaded, the drivers take over control. Consequently, such controllers may not work when driver support is not available for the host operating system. An example is Intel Rapid Storage Technology, implemented on many consumer-level motherboards.

Because some minimal hardware support is involved, this implementation is also called "hardware-assisted software RAID", "hybrid model" RAID, or even "fake RAID". If RAID 5 is supported, the hardware may provide a hardware XOR accelerator. An advantage of this model over the pure software RAID is that—if using a redundancy mode—the boot drive is protected from failure (due to the firmware) during the boot process even before the operating system's drivers take over.

Integrity

Data scrubbing (referred to in some environments as patrol read) involves periodic reading and checking by the RAID controller of all the blocks in an array, including those not otherwise accessed. This detects bad blocks before use. Data scrubbing checks for bad blocks on each storage device in an array, but also uses the redundancy of the array to recover bad blocks on a single drive and to reassign the recovered data to spare blocks elsewhere on the drive.

Frequently, a RAID controller is configured to "drop" a component drive (that is, to assume a component drive has failed) if the drive has been unresponsive for eight seconds or so; this might cause the array controller to drop a good drive because that drive has not been given enough time to complete its internal error recovery procedure. Consequently, using consumer-marketed drives with RAID can be risky, and so-called "enterprise class" drives limit this error recovery time to reduce risk. Western Digital's desktop drives used to have a specific fix. A utility called WDTLER.exe limited a drive's error recovery time. The utility enabled TLER (time limited error recovery), which limits the error recovery time to seven seconds. Around September 2009, Western Digital disabled this feature in their desktop drives (such as the Caviar Black line), making such drives unsuitable for use in RAID configurations. However, Western Digital enterprise class drives are shipped from the factory with TLER enabled. Similar technologies are used by Seagate, Samsung, and Hitachi. For non-RAID usage, an enterprise class drive with a short error recovery timeout that cannot be changed is therefore less suitable than a desktop drive. In late 2010, the Smartmontools program began supporting the configuration of ATA Error Recovery Control, allowing the tool to configure many desktop class hard drives for use in RAID setups.

While RAID may protect against physical drive failure, the data is still exposed to operator, software, hardware, and virus destruction. Many studies cite operator fault as a common source of malfunction, such as a server operator replacing the incorrect drive in a faulty RAID, and disabling the system (even temporarily) in the process.

An array can be overwhelmed by catastrophic failure that exceeds its recovery capacity and the entire array is at risk of physical damage by fire, natural disaster, and human forces, however backups can be stored off site. An array is also vulnerable to controller failure because it is not always possible to migrate it to a new, different controller without data loss.

Weaknesses

Correlated failures

In practice, the drives are often the same age (with similar wear) and subject to the same environment. Since many drive failures are due to mechanical issues (which are more likely on older drives), this violates the assumptions of independent, identical rate of failure amongst drives; failures are in fact statistically correlated. In practice, the chances for a second failure before the first has been recovered (causing data loss) are higher than the chances for random failures. In a study of about 100,000 drives, the probability of two drives in the same cluster failing within one hour was four times larger than predicted by the exponential statistical distribution—which characterizes processes in which events occur continuously and independently at a constant average rate. The probability of two failures in the same 10-hour period was twice as large as predicted by an exponential distribution.

Unrecoverable read errors during rebuild

Unrecoverable read errors (URE) present as sector read failures, also known as latent sector errors (LSE). The associated media assessment measure, unrecoverable bit error (UBE) rate, is typically guaranteed to be less than one bit in 10¹⁵ for enterprise-class drives (SCSI, FC, SAS or SATA), and less than one bit in 10¹⁴ for desktop-class drives (IDE/ATA/PATA or SATA). Increasing drive capacities and large RAID 5 instances have led to the maximum error rates being insufficient to guarantee a successful recovery, due to the high likelihood of such an error occurring on one or more remaining drives during a RAID set rebuild. When rebuilding, parity-based schemes such as RAID 5 are particularly prone to the effects of UREs as they affect not only the sector where they occur, but also reconstructed blocks using that sector for parity computation.

Double-protection parity-based schemes, such as RAID 6, attempt to address this issue by providing redundancy that allows double-drive failures; as a downside, such schemes suffer from elevated write penalty—the number of times the storage medium must be accessed during a single write operation. Schemes that duplicate (mirror) data in a drive-to-drive manner, such as RAID 1 and RAID 10, have a lower risk from UREs than those using parity computation or mirroring between striped sets. Data scrubbing, as a background process, can be used to detect and recover from UREs, effectively reducing the risk of them happening during RAID rebuilds and causing double-drive failures. The recovery of UREs involves remapping of affected underlying disk sectors, utilizing the drive's sector remapping pool; in case of UREs detected during background scrubbing, data redundancy provided by a fully operational RAID set allows the missing data to be reconstructed and rewritten to a remapped sector.

Increasing rebuild time and failure probability

Drive capacity has grown at a much faster rate than transfer speed, and error rates have only fallen a little in comparison. Therefore, larger-capacity drives may take hours if not days to rebuild, during which time other drives may fail or yet undetected read errors may surface. The rebuild time is also limited if the entire array is still in operation at reduced capacity. Given an array with only one redundant drive (which applies to RAID levels 3, 4 and 5, and to "classic" two-drive RAID 1), a second drive failure would cause complete failure of the array. Even though individual drives' mean time between failure (MTBF) have increased over time, this increase has not kept pace with the increased storage capacity of the drives. The time to rebuild the array after a single drive failure, as well as the chance of a second failure during a rebuild, have increased over time.

Some commentators have declared that RAID 6 is only a "band aid" in this respect, because it only kicks the problem a little further down the road. However, according to the 2006 NetApp study of Berriman et al., the chance of failure decreases by a factor of about 3,800 (relative to RAID 5) for a proper implementation of RAID 6, even when using commodity drives. Nevertheless, if the currently observed technology trends remain unchanged, in 2019 a RAID 6 array will have the same chance of failure as its RAID 5 counterpart had in 2010.

Mirroring schemes such as RAID 10 have a bounded recovery time as they require the copy of a single failed drive, compared with parity schemes such as RAID 6, which require the copy of all blocks of the drives in an array set. Triple parity schemes, or triple mirroring, have been suggested as one approach to improve resilience to an additional drive failure during this large rebuild time.

Atomicity

A system crash or other interruption of a write operation can result in states where the parity is inconsistent with the data due to non-atomicity of the write process, such that the parity cannot be used for recovery in the case of a disk failure. This is commonly termed the write hole which is a known data corruption issue in older and low-end RAIDs, caused by interrupted destaging of writes to disk. The write hole can be addressed in a few ways:

• Write-ahead logging.
  • Hardware RAID systems use an onboard nonvolatile cache for this purpose.
  • mdadm can use a dedicated journaling device (to avoid performance penalty, typically, SSDs and NVMs are preferred) for this purpose.
• Write intent logging. mdadm uses a "write-intent-bitmap". If it finds any location marked as incompletely written at startup, it resyncs them. It closes the write hole but does not protect against loss of in-transit data, unlike a full WAL.
• Partial parity. mdadm can save a "partial parity" that, when combined with modified chunks, recovers the original parity. This closes the write hole, but again does not protect against loss of in-transit data.
• Dynamic stripe size. RAID-Z ensures that each block is its own stripe, so every block is complete. Copy-on-write (COW) transactional semantics guard metadata associated with stripes. The downside is IO fragmentation.
• Avoiding overwriting used stripes. bcachefs, which uses a copying garbage collector, chooses this option. COW again protect references to striped data.

Write hole is a little understood and rarely mentioned failure mode for redundant storage systems that do not utilize transactional features. Database researcher Jim Gray wrote "Update in Place is a Poison Apple" during the early days of relational database commercialization.

Write-cache reliability

There are concerns about write-cache reliability, specifically regarding devices equipped with a write-back cache, which is a caching system that reports the data as written as soon as it is written to cache, as opposed to when it is written to the non-volatile medium. If the system experiences a power loss or other major failure, the data may be irrevocably lost from the cache before reaching the non-volatile storage. For this reason good write-back cache implementations include mechanisms, such as redundant battery power, to preserve cache contents across system failures (including power failures) and to flush the cache at system restart time.

Möbius strip

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/M%C3%B6bius_strip 

A Möbius strip made with paper and adhesive tape

In mathematics, a Möbius strip, Möbius band, or Möbius loop is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and August Ferdinand Möbius in 1858, but it had already appeared in Roman mosaics from the third century CE. The Möbius strip is a non-orientable surface, meaning that within it one cannot consistently distinguish clockwise from counterclockwise turns. Every non-orientable surface contains a Möbius strip.

As an abstract topological space, the Möbius strip can be embedded into three-dimensional Euclidean space in many different ways: a clockwise half-twist is different from a counterclockwise half-twist, and it can also be embedded with odd numbers of twists greater than one, or with a knotted centerline. Any two embeddings with the same knot for the centerline and the same number and direction of twists are topologically equivalent. All of these embeddings have only one side, but when embedded in other spaces, the Möbius strip may have two sides. It has only a single boundary curve.

Several geometric constructions of the Möbius strip provide it with additional structure. It can be swept as a ruled surface by a line segment rotating in a rotating plane, with or without self-crossings. A thin paper strip with its ends joined to form a Möbius strip can bend smoothly as a developable surface or be folded flat; the flattened Möbius strips include the trihexaflexagon. The Sudanese Möbius strip is a minimal surface in a hypersphere, and the Meeks Möbius strip is a self-intersecting minimal surface in ordinary Euclidean space. Both the Sudanese Möbius strip and another self-intersecting Möbius strip, the cross-cap, have a circular boundary. A Möbius strip without its boundary, called an open Möbius strip, can form surfaces of constant curvature. Certain highly symmetric spaces whose points represent lines in the plane have the shape of a Möbius strip.

The many applications of Möbius strips include mechanical belts that wear evenly on both sides, dual-track roller coasters whose carriages alternate between the two tracks, and world maps printed so that antipodes appear opposite each other. Möbius strips appear in molecules and devices with novel electrical and electromechanical properties, and have been used to prove impossibility results in social choice theory. In popular culture, Möbius strips appear in artworks by M. C. Escher, Max Bill, and others, and in the design of the recycling symbol. Many architectural concepts have been inspired by the Möbius strip, including the building design for the NASCAR Hall of Fame. Performers including Harry Blackstone Sr. and Thomas Nelson Downs have based stage magic tricks on the properties of the Möbius strip. The canons of J. S. Bach have been analyzed using Möbius strips. Many works of speculative fiction feature Möbius strips; more generally, a plot structure based on the Möbius strip, of events that repeat with a twist, is common in fiction.

History

Mosaic from ancient Sentinum depicting Aion holding a Möbius strip

 

Chain pump with a Möbius drive chain, by Ismail al-Jazari (1206)

The discovery of the Möbius strip as a mathematical object is attributed independently to the German mathematicians Johann Benedict Listing and August Ferdinand Möbius in 1858. However, it had been known long before, both as a physical object and in artistic depictions; in particular, it can be seen in several Roman mosaics from the third century CE. In many cases these merely depict coiled ribbons as boundaries. When the number of coils is odd, these ribbons are Möbius strips, but for an even number of coils they are topologically equivalent to untwisted rings. Therefore, whether the ribbon is a Möbius strip may be coincidental, rather than a deliberate choice. In at least one case, a ribbon with different colors on different sides was drawn with an odd number of coils, forcing its artist to make a clumsy fix at the point where the colors did not match up. Another mosaic from the town of Sentinum (depicted) shows the zodiac, held by the god Aion, as a band with only a single twist. There is no clear evidence that the one-sidedness of this visual representation of celestial time was intentional; it could have been chosen merely as a way to make all of the signs of the zodiac appear on the visible side of the strip. Some other ancient depictions of the ourobouros or of figure-eight-shaped decorations are also alleged to depict Möbius strips, but whether they were intended to depict flat strips of any type is unclear.

Independently of the mathematical tradition, machinists have long known that mechanical belts wear half as quickly when they form Möbius strips, because they use the entire surface of the belt rather than only the inner surface of an untwisted belt. Additionally, such a belt may be less prone to curling from side to side. An early written description of this technique dates to 1871, which is after the first mathematical publications regarding the Möbius strip. Much earlier, an image of a chain pump in a work of Ismail al-Jazari from 1206 depicts a Möbius strip configuration for its drive chain. Another use of this surface was made by seamstresses in Paris (at an unspecified date): they initiated novices by requiring them to stitch a Möbius strip as a collar onto a garment.

Properties

A 2D object traversing once around the Möbius strip returns in mirrored form

The Möbius strip has several curious properties. It is a non-orientable surface: if an asymmetric two-dimensional object slides one time around the strip, it returns to its starting position as its mirror image. In particular, a curved arrow pointing clockwise (↻) would return as an arrow pointing counterclockwise (↺), implying that, within the Möbius strip, it is impossible to consistently define what it means to be clockwise or counterclockwise. It is the simplest non-orientable surface: any other surface is non-orientable if and only if it has a Möbius strip as a subset. Relatedly, when embedded into Euclidean space, the Möbius strip has only one side. A three-dimensional object that slides one time around the surface of the strip is not mirrored, but instead returns to the same point of the strip on what appears locally to be its other side, showing that both positions are really part of a single side. This behavior is different from familiar orientable surfaces in three dimensions such as those modeled by flat sheets of paper, cylindrical drinking straws, or hollow balls, for which one side of the surface is not connected to the other. However, this is a property of its embedding into space rather than an intrinsic property of the Möbius strip itself: there exist other topological spaces in which the Möbius strip can be embedded so that it has two sides. For instance, if the front and back faces of a cube are glued to each other with a left-right mirror reflection, the result is a three-dimensional topological space (the Cartesian product of a Möbius strip with an interval) in which the top and bottom halves of the cube can be separated from each other by a two-sided Möbius strip. In contrast to disks, spheres, and cylinders, for which it is possible to simultaneously embed an uncountable set of disjoint copies into three-dimensional space, only a countable number of Möbius strips can be simultaneously embedded.

A path along the edge of a Möbius strip, traced until it returns to its starting point on the edge, includes all boundary points of the Möbius strip in a single continuous curve. For a Möbius strip formed by gluing and twisting a rectangle, it has twice the length of the centerline of the strip. In this sense, the Möbius strip is different from an untwisted ring and like a circular disk in having only one boundary. A Möbius strip in Euclidean space cannot be moved or stretched into its mirror image; it is a chiral object with right- or left-handedness. Möbius strips with odd numbers of half-twists greater than one, or that are knotted before gluing, are distinct as embedded subsets of three-dimensional space, even though they are all equivalent as two-dimensional topological surfaces. More precisely, two Möbius strips are equivalently embedded in three-dimensional space when their centerlines determine the same knot and they have the same number of twists as each other. With an even number of twists, however, one obtains a different topological surface, called the annulus.

The Möbius strip can be continuously transformed into its centerline, by making it narrower while fixing the points on the centerline. This transformation is an example of a deformation retraction, and its existence means that the Möbius strip has many of the same properties as its centerline, which is topologically a circle. In particular, its fundamental group is the same as the fundamental group of a circle, an infinite cyclic group. Therefore, paths on the Möbius strip that start and end at the same point can be distinguished topologically (up to homotopy) only by the number of times they loop around the strip.

Cutting the centerline produces a double-length two-sided (non-Möbius) strip

 

A single off-center cut produces a Möbius strip (purple) linked with a double-length two-sided strip

Cutting a Möbius strip along the centerline with a pair of scissors yields one long strip with four half-twists in it (relative to an untwisted annulus or cylinder) rather than two separate strips. Two of the half-twists come from the fact that this thinner strip goes two times through the half-twist in the original Möbius strip, and the other two come from the way the two halves of the thinner strip wrap around each other. The result is not a Möbius strip, but instead is topologically equivalent to a cylinder. Cutting this double-twisted strip again along its centerline produces two linked double-twisted strips. If, instead, a Möbius strip is cut lengthwise, a third of the way across its width, it produces two linked strips. One of the two is a central, thinner, Möbius strip, while the other has two half-twists. These interlinked shapes, formed by lengthwise slices of Möbius strips with varying widths, are sometimes called paradromic rings.

Subdivision into six mutually-adjacent regions, bounded by Tietze's graph

 

Solution to the three utilities problem on a Möbius strip

The Möbius strip can be cut into six mutually-adjacent regions, showing that maps on the surface of the Möbius strip can sometimes require six colors, in contrast to the four color theorem for the plane. Six colors are always enough. This result is part of the Ringel–Youngs theorem, which states how many colors each topological surface needs. The edges and vertices of these six regions form Tietze's graph, which is a dual graph on this surface for the six-vertex complete graph but cannot be drawn without crossings on a plane. Another family of graphs that can be embedded on the Möbius strip, but not on the plane, are the Möbius ladders, the boundaries of subdivisions of the Möbius strip into rectangles meeting end-to-end. These include the utility graph, a six-vertex complete bipartite graph whose embedding into the Möbius strip shows that, unlike in the plane, the three utilities problem can be solved on a transparent Möbius strip. The Euler characteristic of the Möbius strip is zero, meaning that for any subdivision of the strip by vertices and edges into regions, the numbers ${\displaystyle V}$, ${\displaystyle E}$, and ${\displaystyle F}$ of vertices, edges, and regions satisfy ${\displaystyle V-E+F=0}$. For instance, Tietze's graph has ${\displaystyle 12}$ vertices, ${\displaystyle 18}$ edges, and ${\displaystyle 6}$ regions; ${\displaystyle 12-18+6=0}$.

Constructions

There are many different ways of defining geometric surfaces with the topology of the Möbius strip, yielding realizations with additional geometric properties.

Sweeping a line segment

A Möbius strip swept out by a rotating line segment in a rotating plane

Plücker's conoid swept out by a different motion of a line segment

One way to embed the Möbius strip in three-dimensional Euclidean space is to sweep it out by a line segment rotating in a plane, which in turn rotates around one of its lines. For the swept surface to meet up with itself after a half-twist, the line segment should rotate around its center at half the angular velocity of the plane's rotation. This can be described as a parametric surface defined by equations for the Cartesian coordinates of its points, $${\displaystyle \begin{array}{rl}x(u,v)& =\left(1+\frac{v}{2}\cos \frac{u}{2}\right)\cos u\\ y(u,v)& =\left(1+\frac{v}{2}\cos \frac{u}{2}\right)\sin u\\ z(u,v)& =\frac{v}{2}\sin \frac{u}{2}\end{array}}$$ for ${\displaystyle 0\le u<2\pi }$ and ${\displaystyle -1\le v\le 1}$, where one parameter ${\displaystyle u}$ describes the rotation angle of the plane around its central axis and the other parameter ${\displaystyle v}$ describes the position of a point along the rotating line segment. This produces a Möbius strip of width 1, whose center circle has radius 1, lies in the ${\displaystyle xy}$-plane and is centered at ${\displaystyle (0,0,0)}$. The same method can produce Möbius strips with any odd number of half-twists, by rotating the segment more quickly in its plane. The rotating segment sweeps out a circular disk in the plane that it rotates within, and the Möbius strip that it generates forms a slice through the solid torus swept out by this disk. Because of the one-sidedness of this slice, the sliced torus remains connected.

A line or line segment swept in a different motion, rotating in a horizontal plane around the origin as it moves up and down, forms Plücker's conoid or cylindroid, an algebraic ruled surface in the form of a self-crossing Möbius strip. It has applications in the design of gears.

Polyhedral surfaces and flat foldings

Trihexaflexagon being flexed

A strip of paper can form a flattened Möbius strip in the plane by folding it at ${\displaystyle {60}^{\circ }}$ angles so that its center line lies along an equilateral triangle, and attaching the ends. The shortest strip for which this is possible consists of three equilateral triangles, folded at the edges where two triangles meet. Its aspect ratio – the ratio of the strip's length to its width – is ${\displaystyle \sqrt{3}\approx 1.73}$, and the same folding method works for any larger aspect ratio. For a strip of nine equilateral triangles, the result is a trihexaflexagon, which can be flexed to reveal different parts of its surface. For strips too short to apply this method directly, one can first "accordion fold" the strip in its wide direction back and forth using an even number of folds. With two folds, for example, a ${\displaystyle 1\times 1}$ strip would become a ${\displaystyle 1\times \frac{1}{3}}$ folded strip whose cross section is in the shape of an 'N' and would remain an 'N' after a half-twist. The narrower accordion-folded strip can then be folded and joined in the same way that a longer strip would be.

Five-vertex polyhedral and flat-folded Möbius strips

The Möbius strip can also be embedded as a polyhedral surface in space or flat-folded in the plane, with only five triangular faces sharing five vertices. In this sense, it is simpler than the cylinder, which requires six triangles and six vertices, even when represented more abstractly as a simplicial complex. A five-triangle Möbius strip can be represented most symmetrically by five of the ten equilateral triangles of a four-dimensional regular simplex. This four-dimensional polyhedral Möbius strip is the only tight Möbius strip, one that is fully four-dimensional and for which all cuts by hyperplanes separate it into two parts that are topologically equivalent to disks or circles.

Other polyhedral embeddings of Möbius strips include one with four convex quadrilaterals as faces, another with three non-convex quadrilateral faces, and one using the vertices and center point of a regular octahedron, with a triangular boundary. Every abstract triangulation of the projective plane can be embedded into 3D as a polyhedral Möbius strip with a triangular boundary after removing one of its faces; an example is the six-vertex projective plane obtained by adding one vertex to the five-vertex Möbius strip, connected by triangles to each of its boundary edges. However, not every abstract triangulation of the Möbius strip can be represented geometrically, as a polyhedral surface. To be realizable, it is necessary and sufficient that there be no two disjoint non-contractible 3-cycles in the triangulation.

Smoothly embedded rectangles

A rectangular Möbius strip, made by attaching the ends of a paper rectangle, can be embedded smoothly into three-dimensional space whenever its aspect ratio is greater than ${\displaystyle \sqrt{3}\approx 1.73}$, the same ratio as for the flat-folded equilateral-triangle version of the Möbius strip. This flat triangular embedding can lift to a smooth^[e] embedding in three dimensions, in which the strip lies flat in three parallel planes between three cylindrical rollers, each tangent to two of the planes. Mathematically, a smoothly embedded sheet of paper can be modeled as a developable surface, that can bend but cannot stretch. As its aspect ratio decreases toward ${\displaystyle \sqrt{3}}$, all smooth embeddings seem to approach the same triangular form.

The lengthwise folds of an accordion-folded flat Möbius strip prevent it from forming a three-dimensional embedding in which the layers are separated from each other and bend smoothly without crumpling or stretching away from the folds. Instead, unlike in the flat-folded case, there is a lower limit to the aspect ratio of smooth rectangular Möbius strips. Their aspect ratio cannot be less than ${\displaystyle \pi /2\approx 1.57}$, even if self-intersections are allowed. Self-intersecting smooth Möbius strips exist for any aspect ratio above this bound. Without self-intersections, the aspect ratio must be at least $${\displaystyle \frac{2}{3}\sqrt{3+2\sqrt{3}}\approx \mathrm{1.695.}}$$

Unsolved problem in mathematics:

Can a ${\displaystyle 12\times 7}$ paper rectangle be glued end-to-end to form a smooth Möbius strip embedded in space? 

For aspect ratios between this bound and ${\displaystyle \sqrt{3}}$, it has been an open problem whether smooth embeddings, without self-intersection, exist. In 2023, Richard Schwartz announced a proof that they do not exist, but this result still awaits peer review and publication. If the requirement of smoothness is relaxed to allow continuously differentiable surfaces, the Nash–Kuiper theorem implies that any two opposite edges of any rectangle can be glued to form an embedded Möbius strip, no matter how small the aspect ratio becomes. The limiting case, a surface obtained from an infinite strip of the plane between two parallel lines, glued with the opposite orientation to each other, is called the unbounded Möbius strip or the real tautological line bundle. Although it has no smooth closed embedding into three-dimensional space, it can be embedded smoothly as a closed subset of four-dimensional Euclidean space.

The minimum-energy shape of a smooth Möbius strip glued from a rectangle does not have a known analytic description, but can be calculated numerically, and has been the subject of much study in plate theory since the initial work on this subject in 1930 by Michael Sadowsky. It is also possible to find algebraic surfaces that contain rectangular developable Möbius strips.

Making the boundary circular

Gluing two Möbius strips to form a Klein bottle

 

A projection of the Sudanese Möbius strip

The edge, or boundary, of a Möbius strip is topologically equivalent to a circle. In common forms of the Möbius strip, it has a different shape from a circle, but it is unknotted, and therefore the whole strip can be stretched without crossing itself to make the edge perfectly circular. One such example is based on the topology of the Klein bottle, a one-sided surface with no boundary that cannot be embedded into three-dimensional space, but can be immersed (allowing the surface to cross itself in certain restricted ways). A Klein bottle is the surface that results when two Möbius strips are glued together edge-to-edge, and – reversing that process – a Klein bottle can be sliced along a carefully chosen cut to produce two Möbius strips. For a form of the Klein bottle known as Lawson's Klein bottle, the curve along which it is sliced can be made circular, resulting in Möbius strips with circular edges.

Lawson's Klein bottle is a self-crossing minimal surface in the unit hypersphere of 4-dimensional space, the set of points of the form $${\displaystyle (\cos \theta \cos \varphi ,\sin \theta \cos \varphi ,\cos 2\theta \sin \varphi ,\sin 2\theta \sin \varphi )}$$ for ${\displaystyle 0\le \theta <\pi ,0\le \varphi <2\pi }$. Half of this Klein bottle, the subset with ${\displaystyle 0\le \varphi <\pi }$, gives a Möbius strip embedded in the hypersphere as a minimal surface with a great circle as its boundary. This embedding is sometimes called the "Sudanese Möbius strip" after topologists Sue Goodman and Daniel Asimov, who discovered it in the 1970s. Geometrically Lawson's Klein bottle can be constructed by sweeping a great circle through a great-circular motion in the 3-sphere, and the Sudanese Möbius strip is obtained by sweeping a semicircle instead of a circle, or equivalently by slicing the Klein bottle along a circle that is perpendicular to all of the swept circles. Stereographic projection transforms this shape from a three-dimensional spherical space into three-dimensional Euclidean space, preserving the circularity of its boundary. The most symmetric projection is obtained by using a projection point that lies on that great circle that runs through the midpoint of each of the semicircles, but produces an unbounded embedding with the projection point removed from its centerline. Instead, leaving the Sudanese Möbius strip unprojected, in the 3-sphere, leaves it with an infinite group of symmetries isomorphic to the orthogonal group ${\displaystyle \mathrm{O}(2)}$, the group of symmetries of a circle.

Schematic depiction of a cross-cap with an open bottom, showing its level sets. This surface crosses itself along the vertical line segment.

The Sudanese Möbius strip extends on all sides of its boundary circle, unavoidably if the surface is to avoid crossing itself. Another form of the Möbius strip, called the cross-cap or crosscap, also has a circular boundary, but otherwise stays on only one side of the plane of this circle, making it more convenient for attaching onto circular holes in other surfaces. In order to do so, it crosses itself. It can be formed by removing a quadrilateral from the top of a hemisphere, orienting the edges of the quadrilateral in alternating directions, and then gluing opposite pairs of these edges consistently with this orientation. The two parts of the surface formed by the two glued pairs of edges cross each other with a pinch point like that of a Whitney umbrella at each end of the crossing segment, the same topological structure seen in Plücker's conoid.

Surfaces of constant curvature

The open Möbius strip is the relative interior of a standard Möbius strip, formed by omitting the points on its boundary edge. It may be given a Riemannian geometry of constant positive, negative, or zero Gaussian curvature. The cases of negative and zero curvature form geodesically complete surfaces, which means that all geodesics ("straight lines" on the surface) may be extended indefinitely in either direction.

Zero curvature

An open strip with zero curvature may be constructed by gluing the opposite sides of a plane strip between two parallel lines, described above as the tautological line bundle. The resulting metric makes the open Möbius strip into a (geodesically) complete flat surface (i.e., having zero Gaussian curvature everywhere). This is the unique metric on the Möbius strip, up to uniform scaling, that is both flat and complete. It is the quotient space of a plane by a glide reflection, and (together with the plane, cylinder, torus, and Klein bottle) is one of only five two-dimensional complete flat manifolds.

Negative curvature

The open Möbius strip also admits complete metrics of constant negative curvature. One way to see this is to begin with the upper half plane (Poincaré) model of the hyperbolic plane, a geometry of constant curvature whose lines are represented in the model by semicircles that meet the ${\displaystyle x}$-axis at right angles. Take the subset of the upper half-plane between any two nested semicircles, and identify the outer semicircle with the left-right reversal of the inner semicircle. The result is topologically a complete and non-compact Möbius strip with constant negative curvature. It is a "nonstandard" complete hyperbolic surface in the sense that it contains a complete hyperbolic half-plane (actually two, on opposite sides of the axis of glide-reflection), and is one of only 13 nonstandard surfaces. Again, this can be understood as the quotient of the hyperbolic plane by a glide reflection.

Positive curvature

A Möbius strip of constant positive curvature cannot be complete, since it is known that the only complete surfaces of constant positive curvature are the sphere and the projective plane. However, in a sense it is only one point away from being a complete surface, as the open Möbius strip is homeomorphic to the once-punctured projective plane, the surface obtained by removing any one point from the projective plane.

The minimal surfaces are described as having constant zero mean curvature instead of constant Gaussian curvature. The Sudanese Möbius strip was constructed as a minimal surface bounded by a great circle in a 3-sphere, but there is also a unique complete (boundaryless) minimal surface immersed in Euclidean space that has the topology of an open Möbius strip. It is called the Meeks Möbius strip, after its 1982 description by William Hamilton Meeks, III. Although globally unstable as a minimal surface, small patches of it, bounded by non-contractible curves within the surface, can form stable embedded Möbius strips as minimal surfaces. Both the Meeks Möbius strip, and every higher-dimensional minimal surface with the topology of the Möbius strip, can be constructed using solutions to the Björling problem, which defines a minimal surface uniquely from its boundary curve and tangent planes along this curve.

Spaces of lines

The family of lines in the plane can be given the structure of a smooth space, with each line represented as a point in this space. The resulting space of lines is topologically equivalent to the open Möbius strip. One way to see this is to extend the Euclidean plane to the real projective plane by adding one more line, the line at infinity. By projective duality the space of lines in the projective plane is equivalent to its space of points, the projective plane itself. Removing the line at infinity, to produce the space of Euclidean lines, punctures this space of projective lines. Therefore, the space of Euclidean lines is a punctured projective plane, which is one of the forms of the open Möbius strip. The space of lines in the hyperbolic plane can be parameterized by unordered pairs of distinct points on a circle, the pairs of points at infinity of each line. This space, again, has the topology of an open Möbius strip.

These spaces of lines are highly symmetric. The symmetries of Euclidean lines include the affine transformations, and the symmetries of hyperbolic lines include the Möbius transformations. The affine transformations and Möbius transformations both form 6-dimensional Lie groups, topological spaces having a compatible algebraic structure describing the composition of symmetries. Because every line in the plane is symmetric to every other line, the open Möbius strip is a homogeneous space, a space with symmetries that take every point to every other point. Homogeneous spaces of Lie groups are called solvmanifolds, and the Möbius strip can be used as a counterexample, showing that not every solvmanifold is a nilmanifold, and that not every solvmanifold can be factored into a direct product of a compact solvmanifold with ${\displaystyle {\mathbb{R}}^n}$. These symmetries also provide another way to construct the Möbius strip itself, as a group model of these Lie groups. A group model consists of a Lie group and a stabilizer subgroup of its action; contracting the cosets of the subgroup to points produces a space with the same topology as the underlying homogenous space. In the case of the symmetries of Euclidean lines, the stabilizer of the ${\displaystyle x}$-axis consists of all symmetries that take the axis to itself. Each line ${\displaystyle \ell }$ corresponds to a coset, the set of symmetries that map ${\displaystyle \ell }$ to the ${\displaystyle x}$-axis. Therefore, the quotient space, a space that has one point per coset and inherits its topology from the space of symmetries, is the same as the space of lines, and is again an open Möbius strip.

Applications

Electrical flow in a Möbius resistor

Beyond the already-discussed applications of Möbius strips to the design of mechanical belts that wear evenly on their entire surface, and of the Plücker conoid to the design of gears, other applications of Möbius strips include:

• Graphene ribbons twisted to form Möbius strips with new electronic characteristics including helical magnetism
• Möbius aromaticity, a property of organic chemicals whose molecular structure forms a cycle, with molecular orbitals aligned along the cycle in the pattern of a Möbius strip
• The Möbius resistor, a strip of conductive material covering the single side of a dielectric Möbius strip, in a way that cancels its own self-inductance
• Resonators with a compact design and a resonant frequency that is half that of identically constructed linear coils
• Polarization patterns in light emerging from a q-plate
• A proof of the impossibility of continuous, anonymous, and unanimous two-party aggregation rules in social choice theory
• Möbius loop roller coasters, a form of dual-tracked roller coaster in which the two tracks spiral around each other an odd number of times, so that the carriages return to the other track than the one they started on
• World maps projected onto a Möbius strip with the convenient properties that there are no east–west boundaries, and that the antipode of any point on the map can be found on the other printed side of the surface at the same point of the Möbius strip

Scientists have also studied the energetics of soap films shaped as Möbius strips, the chemical synthesis of molecules with a Möbius strip shape, and the formation of larger nanoscale Möbius strips using DNA origami.

In popular culture

Endless Twist, Max Bill, 1956, from the Middelheim Open Air Sculpture Museum

Two-dimensional artworks featuring the Möbius strip include an untitled 1947 painting by Corrado Cagli (memorialized in a poem by Charles Olson), and two prints by M. C. Escher: Möbius Band I (1961), depicting three folded flatfish biting each others' tails; and Möbius Band II (1963), depicting ants crawling around a lemniscate-shaped Möbius strip. It is also a popular subject of mathematical sculpture, including works by Max Bill (Endless Ribbon, 1953), José de Rivera (Infinity, 1967), and Sebastián. A trefoil-knotted Möbius strip was used in John Robinson's Immortality (1982). Charles O. Perry's Continuum (1976) is one of several pieces by Perry exploring variations of the Möbius strip.

Recycling symbol

 

Google Drive logo (2012–2014)

 

IMPA logo on stamp

Because of their easily recognized form, Möbius strips are a common element of graphic design. The familiar three-arrow logo for recycling, designed in 1970, is based on the smooth triangular form of the Möbius strip, as was the logo for the environmentally-themed Expo '74. Some variations of the recycling symbol use a different embedding with three half-twists instead of one, and the original version of the Google Drive logo used a flat-folded three-twist Möbius strip, as have other similar designs. The Brazilian Instituto Nacional de Matemática Pura e Aplicada (IMPA) uses a stylized smooth Möbius strip as their logo, and has a matching large sculpture of a Möbius strip on display in their building. The Möbius strip has also featured in the artwork for postage stamps from countries including Brazil, Belgium, the Netherlands, and Switzerland.

NASCAR Hall of Fame entrance

Möbius strips have been a frequent inspiration for the architectural design of buildings and bridges. However, many of these are projects or conceptual designs rather than constructed objects, or stretch their interpretation of the Möbius strip beyond its recognizability as a mathematical form or a functional part of the architecture. An example is the National Library of Kazakhstan, for which a building was planned in the shape of a thickened Möbius strip but refinished with a different design after the original architects pulled out of the project. One notable building incorporating a Möbius strip is the NASCAR Hall of Fame, which is surrounded by a large twisted ribbon of stainless steel acting as a façade and canopy, and evoking the curved shapes of racing tracks. On a smaller scale, Moebius Chair (2006) by Pedro Reyes is a courting bench whose base and sides have the form of a Möbius strip. As a form of mathematics and fiber arts, scarves have been knit into Möbius strips since the work of Elizabeth Zimmermann in the early 1980s. In food styling, Möbius strips have been used for slicing bagels, making loops out of bacon, and creating new shapes for pasta.

Although mathematically the Möbius strip and the fourth dimension are both purely spatial concepts, they have often been invoked in speculative fiction as the basis for a time loop into which unwary victims may become trapped. Examples of this trope include Martin Gardner's "No-Sided Professor" (1946), Armin Joseph Deutsch's "A Subway Named Mobius" (1950) and the film Moebius (1996) based on it. An entire world shaped like a Möbius strip is the setting of Arthur C. Clarke's "The Wall of Darkness" (1946), while conventional Möbius strips are used as clever inventions in multiple stories of William Hazlett Upson from the 1940s. Other works of fiction have been analyzed as having a Möbius strip–like structure, in which elements of the plot repeat with a twist; these include Marcel Proust's In Search of Lost Time (1913–1927), Luigi Pirandello's Six Characters in Search of an Author (1921), Frank Capra's It's a Wonderful Life (1946), John Barth's Lost in the Funhouse (1968), Samuel R. Delany's Dhalgren (1975) and the film Donnie Darko (2001).

One of the musical canons by J. S. Bach, the fifth of 14 canons (BWV 1087) discovered in 1974 in Bach's copy of the Goldberg Variations, features a glide-reflect symmetry in which each voice in the canon repeats, with inverted notes, the same motif from two measures earlier. Because of this symmetry, this canon can be thought of as having its score written on a Möbius strip. In music theory, tones that differ by an octave are generally considered to be equivalent notes, and the space of possible notes forms a circle, the chromatic circle. Because the Möbius strip is the configuration space of two unordered points on a circle, the space of all two-note chords takes the shape of a Möbius strip. This conception, and generalizations to more points, is a significant application of orbifolds to music theory. Modern musical groups taking their name from the Möbius strip include American electronic rock trio Mobius Band and Norwegian progressive rock band Ring Van Möbius.

Möbius strips and their properties have been used in the design of stage magic. One such trick, known as the Afghan bands, uses the fact that the Möbius strip remains in one piece as a single strip when cut lengthwise. It originated in the 1880s, and was very popular in the first half of the twentieth century. Many versions of this trick exist and have been performed by famous illusionists such as Harry Blackstone Sr. and Thomas Nelson Downs.