 | |||||||||||||||
| Platinum | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pronunciation | /ˈplætənəm/ | ||||||||||||||
| Appearance | silvery white | ||||||||||||||
| Standard atomic weight Ar°(Pt) | |||||||||||||||
| |||||||||||||||
| Platinum in the periodic table | |||||||||||||||
| |||||||||||||||
| Atomic number (Z) | 78 | ||||||||||||||
| Group | group 10 | ||||||||||||||
| Period | period 6 | ||||||||||||||
| Block | d-block | ||||||||||||||
| Electron configuration | [Xe] 4f14 5d9 6s1 | ||||||||||||||
| Electrons per shell | 2, 8, 18, 32, 17, 1 | ||||||||||||||
| Physical properties | |||||||||||||||
| Phase at STP | solid | ||||||||||||||
| Melting point | 2041.4 K (1768.3 °C, 3214.9 °F) | ||||||||||||||
| Boiling point | 4098 K (3825 °C, 6917 °F) | ||||||||||||||
| Density (at 20° C) | 21.452 g/cm3 | ||||||||||||||
| when liquid (at m.p.) | 19.77 g/cm3 | ||||||||||||||
| Heat of fusion | 22.17 kJ/mol | ||||||||||||||
| Heat of vaporization | 510 kJ/mol | ||||||||||||||
| Molar heat capacity | 25.86 J/(mol·K) | ||||||||||||||
Vapor pressure
| |||||||||||||||
| Atomic properties | |||||||||||||||
| Oxidation states | −3, −2, −1, 0, +1, +2, +3, +4, +5, +6 (a mildly basic oxide) | ||||||||||||||
| Electronegativity | Pauling scale: 2.28 | ||||||||||||||
| Ionization energies |
| ||||||||||||||
| Atomic radius | empirical: 139 pm | ||||||||||||||
| Covalent radius | 136±5 pm | ||||||||||||||
| Van der Waals radius | 175 pm | ||||||||||||||
 | |||||||||||||||
| Other properties | |||||||||||||||
| Natural occurrence | primordial | ||||||||||||||
| Crystal structure | face-centered cubic (fcc) (cF4) | ||||||||||||||
| Lattice constant | |||||||||||||||
| Thermal expansion | 8.93×10−6/K (at 20 °C) | ||||||||||||||
| Thermal conductivity | 71.6 W/(m⋅K) | ||||||||||||||
| Electrical resistivity | 105 nΩ⋅m (at 20 °C) | ||||||||||||||
| Magnetic ordering | paramagnetic | ||||||||||||||
| Molar magnetic susceptibility | +201.9 × 10−6 cm3/mol (290 K) | ||||||||||||||
| Tensile strength | 125–240 MPa | ||||||||||||||
| Young's modulus | 168 GPa | ||||||||||||||
| Shear modulus | 61 GPa | ||||||||||||||
| Bulk modulus | 230 GPa | ||||||||||||||
| Speed of sound thin rod | 2800 m/s (at r.t.) | ||||||||||||||
| Poisson ratio | 0.38 | ||||||||||||||
| Mohs hardness | 3.5 | ||||||||||||||
| Vickers hardness | 400–550 MPa | ||||||||||||||
| Brinell hardness | 300–500 MPa | ||||||||||||||
| CAS Number | 7440-06-4 | ||||||||||||||
Platinum is a chemical element; it has symbol Pt and atomic number 78. It is a dense, malleable, ductile, highly unreactive, precious, silverish-white transition metal. Its name originates from Spanish platina, a diminutive of plata "silver".
Platinum is a member of the platinum group of elements and group 10 of the periodic table of elements. It has six naturally occurring isotopes. It is one of the rarer elements in Earth's crust, with an average abundance of approximately 5 μg/kg. It occurs in some nickel and copper ores along with some native deposits, mostly in South Africa, which accounts for ~80% of the world production. Because of its scarcity in Earth's crust, only a few hundred tonnes are produced annually, and given its important uses, it is highly valuable and is a major precious metal commodity.
Platinum is one of the least reactive metals. It has remarkable resistance to corrosion, even at high temperatures, and is therefore considered a noble metal. Consequently, platinum is often found chemically uncombined as native platinum. Because it occurs naturally in the alluvial sands of various rivers, it was first used by pre-Columbian South American natives to produce artifacts. It was referenced in European writings as early as the 16th century, but it was not until Antonio de Ulloa published a report on a new metal of Colombian origin in 1748 that it began to be investigated by scientists.
Platinum is used in catalytic converters, laboratory equipment, electrical contacts and electrodes, platinum resistance thermometers, dentistry equipment, and jewelry. Platinum is used in the glass industry to manipulate molten glass, which does not "wet" platinum. As a heavy metal, it leads to health problems upon exposure to its salts; but due to its corrosion resistance, metallic platinum has not been linked to adverse health effects. Compounds containing platinum, such as cisplatin, oxaliplatin and carboplatin, are applied in chemotherapy against certain types of cancer.
Pure platinum is currently less expensive than pure gold, having been so continuously since 2015, but has been twice as expensive or more, mostly prior to 2008. In early 2021, the value of platinum ranged from US$1,055 to US$1,320 per troy ounce.
Characteristics
Physical
Pure platinum is a lustrous, ductile, and malleable, silver-white metal. Platinum is more ductile than gold, silver or copper, thus being the most ductile of pure metals, but it is less malleable than gold. Its physical characteristics and chemical stability make it useful for industrial applications. Its resistance to wear and tarnish is well suited to use in fine jewellery.
Chemical

Platinum has excellent resistance to corrosion. Bulk platinum does not oxidize in air at any temperature, but it forms a thin surface film of PtO2 that can be easily removed by heating to about 400 °C.
The most common oxidation states of platinum are +2 and +4. The +1 and +3 oxidation states are less common, and are often stabilized by metal bonding in bimetallic (or polymetallic) species. Tetracoordinate platinum(II) compounds tend to adopt 16-electron square planar geometries. Although elemental platinum is generally unreactive, it is attacked by chlorine, bromine, iodine, and sulfur. It reacts vigorously with fluorine at 500 °C (932 °F) to form platinum tetrafluoride. Platinum is insoluble in hydrochloric and nitric acid, but dissolves in hot aqua regia (a mixture of nitric and hydrochloric acids), to form aqueous chloroplatinic acid, H2PtCl6:
- Pt + 4 HNO3 + 6 HCl → H2PtCl6 + 4 NO2 + 4 H2O
As a soft acid, the Pt2+ ion has a great affinity for sulfide and sulfur ligands. Numerous DMSO complexes have been reported and care is taken in the choosing of reaction solvents.
In 2007, the German scientist Gerhard Ertl won the Nobel Prize in Chemistry for determining the detailed molecular mechanisms of the catalytic oxidation of carbon monoxide over platinum (catalytic converter).
Isotopes
Platinum has six naturally occurring isotopes: 190
Pt, 192
Pt, 194
Pt, 195
Pt, 196
Pt, and 198
Pt. The most abundant of these is 195
Pt, comprising 33.83% of all platinum. It is the only stable isotope with a non-zero spin. The spin of 1/2 and other favourable magnetic properties of the nucleus are utilised in 195
Pt NMR. Due to its spin and large abundance, 195
Pt satellite peaks are also often observed in 1
H and 31
P NMR spectroscopy (e.g., for Pt-phosphine and Pt-alkyl complexes). 190
Pt is the least abundant at only 0.01%. Of the naturally occurring isotopes, only 190
Pt is unstable, though it decays with a half-life of 6.5×1011 years, causing an activity of 15 Bq/kg of natural platinum. Other isotopes can undergo alpha decay, but their decay has never been observed, therefore they are considered stable.
Platinum also has 38 synthetic isotopes ranging in atomic mass from 165
to 208, making the total number of known isotopes 44. The least stable
of these are 165
Pt and 166
Pt, with half-lives of 260 µs, whereas the most stable is 193
Pt with a half-life of 50 years. Most platinum isotopes decay by some combination of beta decay and alpha decay. 188
Pt, 191
Pt, and 193
Pt decay primarily by electron capture. 190
Pt and 198
Pt are predicted to have energetically favorable double beta decay paths.
Occurrence



Platinum is an extremely rare metal, occurring at a concentration of only 0.005 ppm in Earth's crust. Sometimes mistaken for silver, platinum is often found chemically uncombined as native platinum and as alloy with the other platinum-group metals and iron mostly. Most often the native platinum is found in secondary deposits in alluvial deposits. The alluvial deposits used by pre-Columbian people in the Chocó Department, Colombia are still a source for platinum-group metals. Another large alluvial deposit is in the Ural Mountains, Russia, and it is still mined.
In nickel and copper deposits, platinum-group metals occur as sulfides (e.g., (Pt,Pd)S), tellurides (e.g., PtBiTe), antimonides (PdSb), and arsenides (e.g. PtAs2), and as end alloys with nickel or copper. Platinum arsenide, sperrylite (PtAs2), is a major source of platinum associated with nickel ores in the Sudbury Basin deposit in Ontario, Canada. At Platinum, Alaska, about 17,000 kg (550,000 ozt) was mined between 1927 and 1975. The mine ceased operations in 1990. The rare sulfide mineral cooperite, (Pt,Pd,Ni)S, contains platinum along with palladium and nickel. Cooperite occurs in the Merensky Reef within the Bushveld complex, Gauteng, South Africa.
In 1865, chromites were identified in the Bushveld region of South Africa, followed by the discovery of platinum in 1906. In 1924, the geologist Hans Merensky discovered a large supply of platinum in the Bushveld Igneous Complex in South Africa. The specific layer he found, named the Merensky Reef, contains around 75% of the world's known platinum. The large copper–nickel deposits near Norilsk in Russia, and the Sudbury Basin, Canada, are the two other large deposits. In the Sudbury Basin, the huge quantities of nickel ore processed make up for the fact platinum is present as only 0.5 ppm in the ore. Smaller reserves can be found in the United States, for example in the Absaroka Range in Montana. In 2010, South Africa was the top producer of platinum, with an almost 77% share, followed by Russia at 13%; world production in 2010 was 192,000 kg (423,000 lb).
Large platinum deposits are present in the state of Tamil Nadu, India.
Platinum exists in higher abundances on the Moon and in meteorites. Correspondingly, platinum is found in slightly higher abundances at sites of bolide impact on Earth that are associated with resulting post-impact volcanism, and can be mined economically; the Sudbury Basin is one such example.
Compounds
Halides
Hexachloroplatinic acid mentioned above is probably the most important platinum compound, as it serves as the precursor for many other platinum compounds. By itself, it has various applications in photography, zinc etchings, indelible ink, plating, mirrors, porcelain coloring, and as a catalyst.
Treatment of hexachloroplatinic acid with an ammonium salt, such as ammonium chloride, gives ammonium hexachloroplatinate, which is relatively insoluble in ammonium solutions. Heating this ammonium salt in the presence of hydrogen reduces it to elemental platinum. Potassium hexachloroplatinate is similarly insoluble, and hexachloroplatinic acid has been used in the determination of potassium ions by gravimetry.
When hexachloroplatinic acid is heated, it decomposes through platinum(IV) chloride and platinum(II) chloride to elemental platinum, although the reactions do not occur stepwise:
- (H3O)2PtCl6·nH2O ⇌ PtCl4 + 2 HCl + (n + 2) H2O
- PtCl4 ⇌ PtCl2 + Cl2
- PtCl2 ⇌ Pt + Cl2
All three reactions are reversible. Platinum(II) and platinum(IV) bromides are known as well. Platinum hexafluoride is a strong oxidizer capable of oxidizing oxygen.
Oxides
Platinum(IV) oxide, PtO2, also known as "Adams' catalyst", is a black powder that is soluble in potassium hydroxide (KOH) solutions and concentrated acids. PtO2 and the less common PtO both decompose upon heating. Platinum(II,IV) oxide, Pt3O4, is formed in the following reaction:
- 2 Pt2+ + Pt4+ + 4 O2− → Pt3O4
Other compounds
Unlike palladium acetate, platinum(II) acetate is not commercially available. Where a base is desired, the halides have been used in conjunction with sodium acetate. The use of platinum(II) acetylacetonate has also been reported.
Several barium platinides have been synthesized in which platinum
exhibits negative oxidation states ranging from −1 to −2. These include
BaPt, Ba
3Pt
2, and Ba
2Pt. Caesium platinide, Cs
2Pt, a dark-red transparent crystalline compound has been shown to contain Pt2−
anions. Platinum also exhibits negative oxidation states at surfaces reduced electrochemically.
The negative oxidation states exhibited by platinum are unusual for
metallic elements, and they are attributed to the relativistic
stabilization of the 6s orbitals.
It is predicted that even the cation PtO2+
4 in which platinum exists in the +10 oxidation state may be achievable.
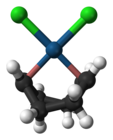
Zeise's salt, containing an ethylene ligand, was one of the first organometallic compounds discovered. Dichloro(cycloocta-1,5-diene)platinum(II) is a commercially available olefin complex, which contains easily displaceable cod ligands ("cod" being an abbreviation of 1,5-cyclooctadiene). The cod complex and the halides are convenient starting points to platinum chemistry.
Cisplatin, or cis-diamminedichloroplatinum(II) is the first of a series of square planar platinum(II)-containing chemotherapy drugs. Others include carboplatin and oxaliplatin. These compounds are capable of crosslinking DNA, and kill cells by similar pathways to alkylating chemotherapeutic agents. (Side effects of cisplatin include nausea and vomiting, hair loss, tinnitus, hearing loss, and nephrotoxicity.)
Organoplatinum
compounds such as the above antitumour agents, as well as soluble
inorganic platinum complexes, are routinely characterised using 195
Pt nuclear magnetic resonance spectroscopy.
-
The hexachloroplatinate ion
-
The anion of Zeise's salt
-
Dichloro(cycloocta-1,5-diene)platinum(II)
-
Cisplatin
History
Early uses
Archaeologists have discovered traces of platinum in the gold used in ancient Egyptian burials as early as 1200 BCE. For example, a small box from burial of Shepenupet II was found to be decorated with gold-platinum hieroglyphics. However, the extent of early Egyptians' knowledge of the metal is unclear. It is quite possible they did not recognize there was platinum in their gold.
The metal was used by Native Americans near modern-day Esmeraldas, Ecuador to produce artifacts of a white gold-platinum alloy. Archeologists usually associate the tradition of platinum-working in South America with the La Tolita Culture (c. 600 BCE – 200 CE), but precise dates and location are difficult, as most platinum artifacts from the area were bought secondhand through the antiquities trade rather than obtained by direct archeological excavation. To work the metal, they would combine gold and platinum powders by sintering. The resulting gold–platinum alloy would then be soft enough to shape with tools. The platinum used in such objects was not the pure element, but rather a naturally occurring mixture of the platinum group metals, with small amounts of palladium, rhodium, and iridium.
European discovery
The first European reference to platinum appears in 1557 in the writings of the Italian humanist Julius Caesar Scaliger as a description of an unknown noble metal found between Darién and Mexico, "which no fire nor any Spanish artifice has yet been able to liquefy". From their first encounters with platinum, the Spanish generally saw the metal as a kind of impurity in gold, and it was treated as such. It was often simply thrown away, and there was an official decree forbidding the adulteration of gold with platinum impurities.


In 1735, Antonio de Ulloa and Jorge Juan y Santacilia saw Native Americans mining platinum while the Spaniards were travelling through Colombia and Peru for eight years. Ulloa and Juan found mines with the whitish metal nuggets and took them home to Spain. Antonio de Ulloa returned to Spain and established the first mineralogy lab in Spain and was the first to systematically study platinum, which was in 1748. His historical account of the expedition included a description of platinum as being neither separable nor calcinable. Ulloa also anticipated the discovery of platinum mines. After publishing the report in 1748, Ulloa did not continue to investigate the new metal. In 1758, he was sent to superintend mercury mining operations in Huancavelica.
In 1741, Charles Wood, a British metallurgist, found various samples of Colombian platinum in Jamaica, which he sent to William Brownrigg for further investigation.
In 1750, after studying the platinum sent to him by Wood, Brownrigg presented a detailed account of the metal to the Royal Society, stating that he had seen no mention of it in any previous accounts of known minerals. Brownrigg also made note of platinum's extremely high melting point and refractoriness toward borax. Other chemists across Europe soon began studying platinum, including Andreas Sigismund Marggraf, Torbern Bergman, Jöns Jakob Berzelius, William Lewis, and Pierre Macquer. In 1752, Henrik Scheffer published a detailed scientific description of the metal, which he referred to as "white gold", including an account of how he succeeded in fusing platinum ore with the aid of arsenic. Scheffer described platinum as being less pliable than gold, but with similar resistance to corrosion.
Means of malleability
Karl von Sickingen researched platinum extensively in 1772. He succeeded in making malleable platinum by alloying it with gold, dissolving the alloy in hot aqua regia, precipitating the platinum with ammonium chloride, igniting the ammonium chloroplatinate, and hammering the resulting finely divided platinum to make it cohere. Franz Karl Achard made the first platinum crucible in 1784. He worked with the platinum by fusing it with arsenic, then later volatilizing the arsenic.
Because the other platinum-family members were not discovered yet (platinum was the first in the list), Scheffer and Sickingen made the false assumption that due to its hardness—which is slightly more than for pure iron—platinum would be a relatively non-pliable material, even brittle at times, when in fact its ductility and malleability are close to that of gold. Their assumptions could not be avoided because the platinum they experimented with was highly contaminated with minute amounts of platinum-family elements such as osmium and iridium, amongst others, which embrittled the platinum alloy. Alloying this impure platinum residue called "plyoxen" with gold was the only solution at the time to obtain a pliable compound, but nowadays, very pure platinum is available and extremely long wires can be drawn from pure platinum, very easily, due to its crystalline structure, which is similar to that of many soft metals.
In 1786, Charles III of Spain provided a library and laboratory to Pierre-François Chabaneau to aid in his research of platinum. Chabaneau succeeded in removing various impurities from the ore, including gold, mercury, lead, copper, and iron. This led him to believe he was working with a single metal, but in truth the ore still contained the yet-undiscovered platinum-group metals. This led to inconsistent results in his experiments. At times, the platinum seemed malleable, but when it was alloyed with iridium, it would be much more brittle. Sometimes the metal was entirely incombustible, but when alloyed with osmium, it would volatilize. After several months, Chabaneau succeeded in producing 23 kilograms of pure, malleable platinum by hammering and compressing the sponge form while white-hot. Chabeneau realized the infusibility of platinum would lend value to objects made of it, and so started a business with Joaquín Cabezas producing platinum ingots and utensils. This started what is known as the "platinum age" in Spain.
Production


Platinum, along with the rest of the platinum-group metals, is obtained commercially as a by-product from nickel and copper mining and processing. During electrorefining of copper, noble metals such as silver, gold and the platinum-group metals as well as selenium and tellurium settle to the bottom of the cell as "anode mud", which forms the starting point for the extraction of the platinum-group metals.
If pure platinum is found in placer deposits or other ores, it is isolated from them by various methods of subtracting impurities. Because platinum is significantly denser than many of its impurities, the lighter impurities can be removed by simply floating them away in a liquid. Platinum is paramagnetic, whereas nickel and iron are both ferromagnetic. These two impurities are thus removed by running an electromagnet over the mixture. Because platinum has a higher melting point than most other substances, many impurities can be burned or melted away without melting the platinum. Finally, platinum is resistant to hydrochloric and sulfuric acids, whereas other substances are readily attacked by them. Metal impurities can be removed by stirring the mixture in either of the two acids and recovering the remaining platinum.
One suitable method for purification for the raw platinum, which contains platinum, gold, and the other platinum-group metals, is to process it with aqua regia, in which palladium, gold and platinum are dissolved, whereas osmium, iridium, ruthenium and rhodium stay unreacted. The gold is precipitated by the addition of iron(II) chloride and after filtering off the gold, the platinum is precipitated as ammonium chloroplatinate by the addition of ammonium chloride. Ammonium chloroplatinate can be converted to platinum by heating. Unprecipitated hexachloroplatinate(IV) may be reduced with elemental zinc, and a similar method is suitable for small scale recovery of platinum from laboratory residues. Mining and refining platinum has environmental impacts.
Applications

Of the 218 tonnes of platinum sold in 2014, 98 tonnes were used for vehicle emissions control devices (45%), 74.7 tonnes for jewelry (34%), 20.0 tonnes for chemical production and petroleum refining (9.2%), and 5.85 tonnes for electrical applications such as hard disk drives (2.7%). The remaining 28.9 tonnes went to various other minor applications, such as medicine and biomedicine, glassmaking equipment, investment, electrodes, anticancer drugs, oxygen sensors, spark plugs and turbine engines.
Catalyst
The most common use of platinum is as a catalyst in chemical reactions, often as platinum black. It has been employed as a catalyst since the early 19th century, when platinum powder was used to catalyze the ignition of hydrogen. Its most important application is in automobiles as a catalytic converter, which allows the complete combustion of low concentrations of unburned hydrocarbons from the exhaust into carbon dioxide and water vapor. Platinum is also used in the petroleum industry as a catalyst in a number of separate processes, but especially in catalytic reforming of straight-run naphthas into higher-octane gasoline that becomes rich in aromatic compounds. PtO2, also known as Adams' catalyst, is used as a hydrogenation catalyst, specifically for vegetable oils. Platinum also strongly catalyzes the decomposition of hydrogen peroxide into water and oxygen and it is used in fuel cells as a catalyst for the reduction of oxygen.
Green energy transition
As a fuel cell catalyst, platinum enables hydrogen and oxygen reactions to take place at an optimum rate. It is used in platinum-based proton exchange memebrane (PEM) technologies required in green hydrogen production as well as fuel cell electric vehicle adoption (FCEV).
Standard

From 1889 to 1960, the meter was defined as the length of a platinum-iridium (90:10) alloy bar, known as the international prototype meter. The previous bar was made of platinum in 1799. Until May 2019, the kilogram was defined as the mass of the international prototype of the kilogram, a cylinder of the same platinum-iridium alloy made in 1879.
The Standard Platinum Resistance Thermometer (SPRT) is one of the four types of thermometers used to define the International Temperature Scale of 1990 (ITS-90), the international calibration standard for temperature measurements. The resistance wire in the thermometer is made of pure platinum (NIST manufactured the wires from platinum bar stock with a chemical purity of 99.999% by weight). In addition to laboratory uses, Platinum Resistance Thermometry (PRT) also has many industrial applications, industrial standards include ASTM E1137 and IEC 60751.
The standard hydrogen electrode also uses a platinized platinum electrode due to its corrosion resistance, and other attributes.
As an investment
Platinum is a precious metal commodity; its bullion has the ISO currency code of XPT. Coins, bars, and ingots are traded or collected. Platinum finds use in jewellery, usually as a 90–95% alloy, due to its inertness. It is used for this purpose for its prestige and inherent bullion value. Jewellery trade publications advise jewellers to present minute surface scratches (which they term patina) as a desirable feature in an attempt to enhance value of platinum products.
In watchmaking, Vacheron Constantin, Patek Philippe, Rolex, Breitling, and other companies use platinum for producing their limited edition watch series. Watchmakers appreciate the unique properties of platinum, as it neither tarnishes nor wears out (the latter quality relative to gold).
During periods of sustained economic stability and growth, the price of platinum tends to be as much as twice the price of gold, whereas during periods of economic uncertainty, the price of platinum tends to decrease due to reduced industrial demand, falling below the price of gold. Gold prices are more stable in slow economic times, as gold is considered a safe haven. Although gold is also used in industrial applications, especially in electronics due to its use as a conductor, its demand is not so driven by industrial uses. In the 18th century, platinum's rarity made King Louis XV of France declare it the only metal fit for a king.
-
1,000 cubic centimeters of 99.9% pure platinum, worth about US$696,000 at 29 Jun 2016 prices
-
Platinum price 1970–2022
Other uses
In the laboratory, platinum wire is used for electrodes; platinum pans and supports are used in thermogravimetric analysis because of the stringent requirements of chemical inertness upon heating to high temperatures (~1000 °C). Platinum is used as an alloying agent for various metal products, including fine wires, noncorrosive laboratory containers, medical instruments, dental prostheses, electrical contacts, and thermocouples. Platinum-cobalt, an alloy of roughly three parts platinum and one part cobalt, is used to make relatively strong permanent magnets. Platinum-based anodes are used in ships, pipelines, and steel piers. Platinum drugs are used to treat a wide variety of cancers, including testicular and ovarian carcinomas, melanoma, small-cell and non-small-cell lung cancer, myelomas and lymphomas.
Symbol of prestige in marketing
Platinum's rarity as a metal has caused advertisers to associate it with exclusivity and wealth. "Platinum" debit and credit cards have greater privileges than "gold" cards. "Platinum awards" are the second highest possible, ranking above "gold", "silver" and "bronze", but below diamond. For example, in the United States, a musical album that has sold more than 1 million copies will be credited as "platinum", whereas an album that has sold more than 10 million copies will be certified as "diamond". Some products, such as blenders and vehicles, with a silvery-white color are identified as "platinum". Platinum is considered a precious metal, although its use is not as common as the use of gold or silver. The frame of the Crown of Queen Elizabeth The Queen Mother, manufactured for her coronation as Consort of King George VI, is made of platinum. It was the first British crown to be made of this particular metal.
Health problems
According to the Centers for Disease Control and Prevention, short-term exposure to platinum salts may cause irritation of the eyes, nose, and throat, and long-term exposure may cause both respiratory and skin allergies. The current OSHA standard is 2 micrograms per cubic meter of air averaged over an 8-hour work shift. The National Institute for Occupational Safety and Health has set a recommended exposure limit (REL) for platinum as 1 mg/m3 over an 8-hour workday.
As platinum is a catalyst in the manufacture of the silicone rubber and gel components of several types of medical implants (breast implants, joint replacement prosthetics, artificial lumbar discs, vascular access ports, etc.), the possibility that platinum could enter the body and cause adverse effects has merited study. The Food and Drug Administration and other institutions have reviewed the issue and found no evidence to suggest toxicity in vivo. Chemically unbounded platinum has been identified by the FDA as a "fake cancer 'cure'". The misunderstanding is created by healthcare workers who are using inappropriately the name of the metal as a slang term for platinum-based chemotherapy medications like cisplatin. They are platinum compounds, not the metal itself.
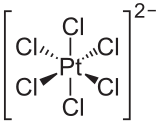


![1,000 cubic centimeters of 99.9% pure platinum, worth about US$696,000 at 29 Jun 2016 prices[88]](https://upload.wikimedia.org/wikipedia/commons/thumb/4/48/One_litre_of_Platinum.jpg/200px-One_litre_of_Platinum.jpg)











![{\displaystyle {\mathbf {K} }_{\mathrm {T} }={\frac {[cis-enol]}{[diketo]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9921ac02a5c977cb96d9a14a8fd9ffe9794422f)

