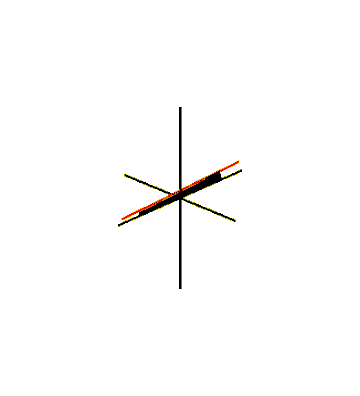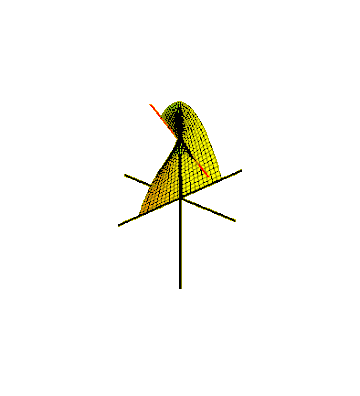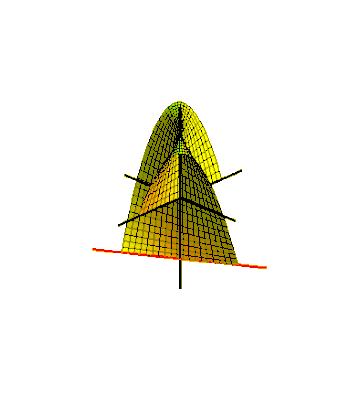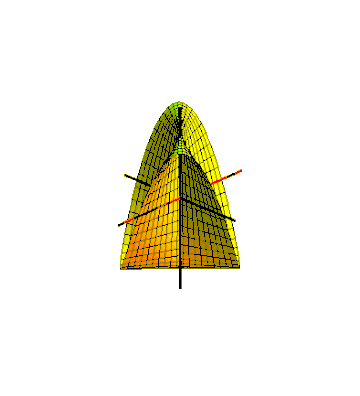Möbius strip

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/M%C3%B6bius_strip 

A Möbius strip made with paper and adhesive tape

In mathematics, a Möbius strip, Möbius band, or Möbius loop is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and August Ferdinand Möbius in 1858, but it had already appeared in Roman mosaics from the third century CE. The Möbius strip is a non-orientable surface, meaning that within it one cannot consistently distinguish clockwise from counterclockwise turns. Every non-orientable surface contains a Möbius strip.

As an abstract topological space, the Möbius strip can be embedded into three-dimensional Euclidean space in many different ways: a clockwise half-twist is different from a counterclockwise half-twist, and it can also be embedded with odd numbers of twists greater than one, or with a knotted centerline. Any two embeddings with the same knot for the centerline and the same number and direction of twists are topologically equivalent. All of these embeddings have only one side, but when embedded in other spaces, the Möbius strip may have two sides. It has only a single boundary curve.

Several geometric constructions of the Möbius strip provide it with additional structure. It can be swept as a ruled surface by a line segment rotating in a rotating plane, with or without self-crossings. A thin paper strip with its ends joined to form a Möbius strip can bend smoothly as a developable surface or be folded flat; the flattened Möbius strips include the trihexaflexagon. The Sudanese Möbius strip is a minimal surface in a hypersphere, and the Meeks Möbius strip is a self-intersecting minimal surface in ordinary Euclidean space. Both the Sudanese Möbius strip and another self-intersecting Möbius strip, the cross-cap, have a circular boundary. A Möbius strip without its boundary, called an open Möbius strip, can form surfaces of constant curvature. Certain highly symmetric spaces whose points represent lines in the plane have the shape of a Möbius strip.

The many applications of Möbius strips include mechanical belts that wear evenly on both sides, dual-track roller coasters whose carriages alternate between the two tracks, and world maps printed so that antipodes appear opposite each other. Möbius strips appear in molecules and devices with novel electrical and electromechanical properties, and have been used to prove impossibility results in social choice theory. In popular culture, Möbius strips appear in artworks by M. C. Escher, Max Bill, and others, and in the design of the recycling symbol. Many architectural concepts have been inspired by the Möbius strip, including the building design for the NASCAR Hall of Fame. Performers including Harry Blackstone Sr. and Thomas Nelson Downs have based stage magic tricks on the properties of the Möbius strip. The canons of J. S. Bach have been analyzed using Möbius strips. Many works of speculative fiction feature Möbius strips; more generally, a plot structure based on the Möbius strip, of events that repeat with a twist, is common in fiction.

History

Mosaic from ancient Sentinum depicting Aion holding a Möbius strip

 

Chain pump with a Möbius drive chain, by Ismail al-Jazari (1206)

The discovery of the Möbius strip as a mathematical object is attributed independently to the German mathematicians Johann Benedict Listing and August Ferdinand Möbius in 1858. However, it had been known long before, both as a physical object and in artistic depictions; in particular, it can be seen in several Roman mosaics from the third century CE. In many cases these merely depict coiled ribbons as boundaries. When the number of coils is odd, these ribbons are Möbius strips, but for an even number of coils they are topologically equivalent to untwisted rings. Therefore, whether the ribbon is a Möbius strip may be coincidental, rather than a deliberate choice. In at least one case, a ribbon with different colors on different sides was drawn with an odd number of coils, forcing its artist to make a clumsy fix at the point where the colors did not match up. Another mosaic from the town of Sentinum (depicted) shows the zodiac, held by the god Aion, as a band with only a single twist. There is no clear evidence that the one-sidedness of this visual representation of celestial time was intentional; it could have been chosen merely as a way to make all of the signs of the zodiac appear on the visible side of the strip. Some other ancient depictions of the ourobouros or of figure-eight-shaped decorations are also alleged to depict Möbius strips, but whether they were intended to depict flat strips of any type is unclear.

Independently of the mathematical tradition, machinists have long known that mechanical belts wear half as quickly when they form Möbius strips, because they use the entire surface of the belt rather than only the inner surface of an untwisted belt. Additionally, such a belt may be less prone to curling from side to side. An early written description of this technique dates to 1871, which is after the first mathematical publications regarding the Möbius strip. Much earlier, an image of a chain pump in a work of Ismail al-Jazari from 1206 depicts a Möbius strip configuration for its drive chain. Another use of this surface was made by seamstresses in Paris (at an unspecified date): they initiated novices by requiring them to stitch a Möbius strip as a collar onto a garment.

Properties

A 2D object traversing once around the Möbius strip returns in mirrored form

The Möbius strip has several curious properties. It is a non-orientable surface: if an asymmetric two-dimensional object slides one time around the strip, it returns to its starting position as its mirror image. In particular, a curved arrow pointing clockwise (↻) would return as an arrow pointing counterclockwise (↺), implying that, within the Möbius strip, it is impossible to consistently define what it means to be clockwise or counterclockwise. It is the simplest non-orientable surface: any other surface is non-orientable if and only if it has a Möbius strip as a subset. Relatedly, when embedded into Euclidean space, the Möbius strip has only one side. A three-dimensional object that slides one time around the surface of the strip is not mirrored, but instead returns to the same point of the strip on what appears locally to be its other side, showing that both positions are really part of a single side. This behavior is different from familiar orientable surfaces in three dimensions such as those modeled by flat sheets of paper, cylindrical drinking straws, or hollow balls, for which one side of the surface is not connected to the other. However, this is a property of its embedding into space rather than an intrinsic property of the Möbius strip itself: there exist other topological spaces in which the Möbius strip can be embedded so that it has two sides. For instance, if the front and back faces of a cube are glued to each other with a left-right mirror reflection, the result is a three-dimensional topological space (the Cartesian product of a Möbius strip with an interval) in which the top and bottom halves of the cube can be separated from each other by a two-sided Möbius strip. In contrast to disks, spheres, and cylinders, for which it is possible to simultaneously embed an uncountable set of disjoint copies into three-dimensional space, only a countable number of Möbius strips can be simultaneously embedded.

A path along the edge of a Möbius strip, traced until it returns to its starting point on the edge, includes all boundary points of the Möbius strip in a single continuous curve. For a Möbius strip formed by gluing and twisting a rectangle, it has twice the length of the centerline of the strip. In this sense, the Möbius strip is different from an untwisted ring and like a circular disk in having only one boundary. A Möbius strip in Euclidean space cannot be moved or stretched into its mirror image; it is a chiral object with right- or left-handedness. Möbius strips with odd numbers of half-twists greater than one, or that are knotted before gluing, are distinct as embedded subsets of three-dimensional space, even though they are all equivalent as two-dimensional topological surfaces. More precisely, two Möbius strips are equivalently embedded in three-dimensional space when their centerlines determine the same knot and they have the same number of twists as each other. With an even number of twists, however, one obtains a different topological surface, called the annulus.

The Möbius strip can be continuously transformed into its centerline, by making it narrower while fixing the points on the centerline. This transformation is an example of a deformation retraction, and its existence means that the Möbius strip has many of the same properties as its centerline, which is topologically a circle. In particular, its fundamental group is the same as the fundamental group of a circle, an infinite cyclic group. Therefore, paths on the Möbius strip that start and end at the same point can be distinguished topologically (up to homotopy) only by the number of times they loop around the strip.

Cutting the centerline produces a double-length two-sided (non-Möbius) strip

 

A single off-center cut produces a Möbius strip (purple) linked with a double-length two-sided strip

Cutting a Möbius strip along the centerline with a pair of scissors yields one long strip with four half-twists in it (relative to an untwisted annulus or cylinder) rather than two separate strips. Two of the half-twists come from the fact that this thinner strip goes two times through the half-twist in the original Möbius strip, and the other two come from the way the two halves of the thinner strip wrap around each other. The result is not a Möbius strip, but instead is topologically equivalent to a cylinder. Cutting this double-twisted strip again along its centerline produces two linked double-twisted strips. If, instead, a Möbius strip is cut lengthwise, a third of the way across its width, it produces two linked strips. One of the two is a central, thinner, Möbius strip, while the other has two half-twists. These interlinked shapes, formed by lengthwise slices of Möbius strips with varying widths, are sometimes called paradromic rings.

Subdivision into six mutually-adjacent regions, bounded by Tietze's graph

 

Solution to the three utilities problem on a Möbius strip

The Möbius strip can be cut into six mutually-adjacent regions, showing that maps on the surface of the Möbius strip can sometimes require six colors, in contrast to the four color theorem for the plane. Six colors are always enough. This result is part of the Ringel–Youngs theorem, which states how many colors each topological surface needs. The edges and vertices of these six regions form Tietze's graph, which is a dual graph on this surface for the six-vertex complete graph but cannot be drawn without crossings on a plane. Another family of graphs that can be embedded on the Möbius strip, but not on the plane, are the Möbius ladders, the boundaries of subdivisions of the Möbius strip into rectangles meeting end-to-end. These include the utility graph, a six-vertex complete bipartite graph whose embedding into the Möbius strip shows that, unlike in the plane, the three utilities problem can be solved on a transparent Möbius strip. The Euler characteristic of the Möbius strip is zero, meaning that for any subdivision of the strip by vertices and edges into regions, the numbers ${\displaystyle V}$, ${\displaystyle E}$, and ${\displaystyle F}$ of vertices, edges, and regions satisfy ${\displaystyle V-E+F=0}$. For instance, Tietze's graph has ${\displaystyle 12}$ vertices, ${\displaystyle 18}$ edges, and ${\displaystyle 6}$ regions; ${\displaystyle 12-18+6=0}$.

Constructions

There are many different ways of defining geometric surfaces with the topology of the Möbius strip, yielding realizations with additional geometric properties.

Sweeping a line segment

A Möbius strip swept out by a rotating line segment in a rotating plane

Plücker's conoid swept out by a different motion of a line segment

One way to embed the Möbius strip in three-dimensional Euclidean space is to sweep it out by a line segment rotating in a plane, which in turn rotates around one of its lines. For the swept surface to meet up with itself after a half-twist, the line segment should rotate around its center at half the angular velocity of the plane's rotation. This can be described as a parametric surface defined by equations for the Cartesian coordinates of its points, $${\displaystyle \begin{array}{rl}x(u,v)& =\left(1+\frac{v}{2}\cos \frac{u}{2}\right)\cos u\\ y(u,v)& =\left(1+\frac{v}{2}\cos \frac{u}{2}\right)\sin u\\ z(u,v)& =\frac{v}{2}\sin \frac{u}{2}\end{array}}$$ for ${\displaystyle 0\le u<2\pi }$ and ${\displaystyle -1\le v\le 1}$, where one parameter ${\displaystyle u}$ describes the rotation angle of the plane around its central axis and the other parameter ${\displaystyle v}$ describes the position of a point along the rotating line segment. This produces a Möbius strip of width 1, whose center circle has radius 1, lies in the ${\displaystyle xy}$-plane and is centered at ${\displaystyle (0,0,0)}$. The same method can produce Möbius strips with any odd number of half-twists, by rotating the segment more quickly in its plane. The rotating segment sweeps out a circular disk in the plane that it rotates within, and the Möbius strip that it generates forms a slice through the solid torus swept out by this disk. Because of the one-sidedness of this slice, the sliced torus remains connected.

A line or line segment swept in a different motion, rotating in a horizontal plane around the origin as it moves up and down, forms Plücker's conoid or cylindroid, an algebraic ruled surface in the form of a self-crossing Möbius strip. It has applications in the design of gears.

Polyhedral surfaces and flat foldings

Trihexaflexagon being flexed

A strip of paper can form a flattened Möbius strip in the plane by folding it at ${\displaystyle {60}^{\circ }}$ angles so that its center line lies along an equilateral triangle, and attaching the ends. The shortest strip for which this is possible consists of three equilateral triangles, folded at the edges where two triangles meet. Its aspect ratio – the ratio of the strip's length to its width – is ${\displaystyle \sqrt{3}\approx 1.73}$, and the same folding method works for any larger aspect ratio. For a strip of nine equilateral triangles, the result is a trihexaflexagon, which can be flexed to reveal different parts of its surface. For strips too short to apply this method directly, one can first "accordion fold" the strip in its wide direction back and forth using an even number of folds. With two folds, for example, a ${\displaystyle 1\times 1}$ strip would become a ${\displaystyle 1\times \frac{1}{3}}$ folded strip whose cross section is in the shape of an 'N' and would remain an 'N' after a half-twist. The narrower accordion-folded strip can then be folded and joined in the same way that a longer strip would be.

Five-vertex polyhedral and flat-folded Möbius strips

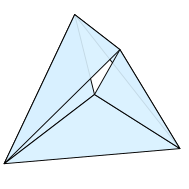
The Möbius strip can also be embedded as a polyhedral surface in space or flat-folded in the plane, with only five triangular faces sharing five vertices. In this sense, it is simpler than the cylinder, which requires six triangles and six vertices, even when represented more abstractly as a simplicial complex. A five-triangle Möbius strip can be represented most symmetrically by five of the ten equilateral triangles of a four-dimensional regular simplex. This four-dimensional polyhedral Möbius strip is the only tight Möbius strip, one that is fully four-dimensional and for which all cuts by hyperplanes separate it into two parts that are topologically equivalent to disks or circles.

Other polyhedral embeddings of Möbius strips include one with four convex quadrilaterals as faces, another with three non-convex quadrilateral faces, and one using the vertices and center point of a regular octahedron, with a triangular boundary. Every abstract triangulation of the projective plane can be embedded into 3D as a polyhedral Möbius strip with a triangular boundary after removing one of its faces; an example is the six-vertex projective plane obtained by adding one vertex to the five-vertex Möbius strip, connected by triangles to each of its boundary edges. However, not every abstract triangulation of the Möbius strip can be represented geometrically, as a polyhedral surface. To be realizable, it is necessary and sufficient that there be no two disjoint non-contractible 3-cycles in the triangulation.

Smoothly embedded rectangles

A rectangular Möbius strip, made by attaching the ends of a paper rectangle, can be embedded smoothly into three-dimensional space whenever its aspect ratio is greater than ${\displaystyle \sqrt{3}\approx 1.73}$, the same ratio as for the flat-folded equilateral-triangle version of the Möbius strip. This flat triangular embedding can lift to a smooth^[e] embedding in three dimensions, in which the strip lies flat in three parallel planes between three cylindrical rollers, each tangent to two of the planes. Mathematically, a smoothly embedded sheet of paper can be modeled as a developable surface, that can bend but cannot stretch. As its aspect ratio decreases toward ${\displaystyle \sqrt{3}}$, all smooth embeddings seem to approach the same triangular form.

The lengthwise folds of an accordion-folded flat Möbius strip prevent it from forming a three-dimensional embedding in which the layers are separated from each other and bend smoothly without crumpling or stretching away from the folds. Instead, unlike in the flat-folded case, there is a lower limit to the aspect ratio of smooth rectangular Möbius strips. Their aspect ratio cannot be less than ${\displaystyle \pi /2\approx 1.57}$, even if self-intersections are allowed. Self-intersecting smooth Möbius strips exist for any aspect ratio above this bound. Without self-intersections, the aspect ratio must be at least $${\displaystyle \frac{2}{3}\sqrt{3+2\sqrt{3}}\approx \mathrm{1.695.}}$$

Unsolved problem in mathematics:

Can a ${\displaystyle 12\times 7}$ paper rectangle be glued end-to-end to form a smooth Möbius strip embedded in space? 

For aspect ratios between this bound and ${\displaystyle \sqrt{3}}$, it has been an open problem whether smooth embeddings, without self-intersection, exist. In 2023, Richard Schwartz announced a proof that they do not exist, but this result still awaits peer review and publication. If the requirement of smoothness is relaxed to allow continuously differentiable surfaces, the Nash–Kuiper theorem implies that any two opposite edges of any rectangle can be glued to form an embedded Möbius strip, no matter how small the aspect ratio becomes. The limiting case, a surface obtained from an infinite strip of the plane between two parallel lines, glued with the opposite orientation to each other, is called the unbounded Möbius strip or the real tautological line bundle. Although it has no smooth closed embedding into three-dimensional space, it can be embedded smoothly as a closed subset of four-dimensional Euclidean space.

The minimum-energy shape of a smooth Möbius strip glued from a rectangle does not have a known analytic description, but can be calculated numerically, and has been the subject of much study in plate theory since the initial work on this subject in 1930 by Michael Sadowsky. It is also possible to find algebraic surfaces that contain rectangular developable Möbius strips.

Making the boundary circular

Gluing two Möbius strips to form a Klein bottle

 

A projection of the Sudanese Möbius strip

The edge, or boundary, of a Möbius strip is topologically equivalent to a circle. In common forms of the Möbius strip, it has a different shape from a circle, but it is unknotted, and therefore the whole strip can be stretched without crossing itself to make the edge perfectly circular. One such example is based on the topology of the Klein bottle, a one-sided surface with no boundary that cannot be embedded into three-dimensional space, but can be immersed (allowing the surface to cross itself in certain restricted ways). A Klein bottle is the surface that results when two Möbius strips are glued together edge-to-edge, and – reversing that process – a Klein bottle can be sliced along a carefully chosen cut to produce two Möbius strips. For a form of the Klein bottle known as Lawson's Klein bottle, the curve along which it is sliced can be made circular, resulting in Möbius strips with circular edges.

Lawson's Klein bottle is a self-crossing minimal surface in the unit hypersphere of 4-dimensional space, the set of points of the form $${\displaystyle (\cos \theta \cos \varphi ,\sin \theta \cos \varphi ,\cos 2\theta \sin \varphi ,\sin 2\theta \sin \varphi )}$$ for ${\displaystyle 0\le \theta <\pi ,0\le \varphi <2\pi }$. Half of this Klein bottle, the subset with ${\displaystyle 0\le \varphi <\pi }$, gives a Möbius strip embedded in the hypersphere as a minimal surface with a great circle as its boundary. This embedding is sometimes called the "Sudanese Möbius strip" after topologists Sue Goodman and Daniel Asimov, who discovered it in the 1970s. Geometrically Lawson's Klein bottle can be constructed by sweeping a great circle through a great-circular motion in the 3-sphere, and the Sudanese Möbius strip is obtained by sweeping a semicircle instead of a circle, or equivalently by slicing the Klein bottle along a circle that is perpendicular to all of the swept circles. Stereographic projection transforms this shape from a three-dimensional spherical space into three-dimensional Euclidean space, preserving the circularity of its boundary. The most symmetric projection is obtained by using a projection point that lies on that great circle that runs through the midpoint of each of the semicircles, but produces an unbounded embedding with the projection point removed from its centerline. Instead, leaving the Sudanese Möbius strip unprojected, in the 3-sphere, leaves it with an infinite group of symmetries isomorphic to the orthogonal group ${\displaystyle \mathrm{O}(2)}$, the group of symmetries of a circle.

Schematic depiction of a cross-cap with an open bottom, showing its level sets. This surface crosses itself along the vertical line segment.

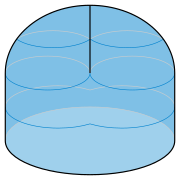
The Sudanese Möbius strip extends on all sides of its boundary circle, unavoidably if the surface is to avoid crossing itself. Another form of the Möbius strip, called the cross-cap or crosscap, also has a circular boundary, but otherwise stays on only one side of the plane of this circle, making it more convenient for attaching onto circular holes in other surfaces. In order to do so, it crosses itself. It can be formed by removing a quadrilateral from the top of a hemisphere, orienting the edges of the quadrilateral in alternating directions, and then gluing opposite pairs of these edges consistently with this orientation. The two parts of the surface formed by the two glued pairs of edges cross each other with a pinch point like that of a Whitney umbrella at each end of the crossing segment, the same topological structure seen in Plücker's conoid.

Surfaces of constant curvature

The open Möbius strip is the relative interior of a standard Möbius strip, formed by omitting the points on its boundary edge. It may be given a Riemannian geometry of constant positive, negative, or zero Gaussian curvature. The cases of negative and zero curvature form geodesically complete surfaces, which means that all geodesics ("straight lines" on the surface) may be extended indefinitely in either direction.

Zero curvature

An open strip with zero curvature may be constructed by gluing the opposite sides of a plane strip between two parallel lines, described above as the tautological line bundle. The resulting metric makes the open Möbius strip into a (geodesically) complete flat surface (i.e., having zero Gaussian curvature everywhere). This is the unique metric on the Möbius strip, up to uniform scaling, that is both flat and complete. It is the quotient space of a plane by a glide reflection, and (together with the plane, cylinder, torus, and Klein bottle) is one of only five two-dimensional complete flat manifolds.

Negative curvature

The open Möbius strip also admits complete metrics of constant negative curvature. One way to see this is to begin with the upper half plane (Poincaré) model of the hyperbolic plane, a geometry of constant curvature whose lines are represented in the model by semicircles that meet the ${\displaystyle x}$-axis at right angles. Take the subset of the upper half-plane between any two nested semicircles, and identify the outer semicircle with the left-right reversal of the inner semicircle. The result is topologically a complete and non-compact Möbius strip with constant negative curvature. It is a "nonstandard" complete hyperbolic surface in the sense that it contains a complete hyperbolic half-plane (actually two, on opposite sides of the axis of glide-reflection), and is one of only 13 nonstandard surfaces. Again, this can be understood as the quotient of the hyperbolic plane by a glide reflection.

Positive curvature

A Möbius strip of constant positive curvature cannot be complete, since it is known that the only complete surfaces of constant positive curvature are the sphere and the projective plane. However, in a sense it is only one point away from being a complete surface, as the open Möbius strip is homeomorphic to the once-punctured projective plane, the surface obtained by removing any one point from the projective plane.

The minimal surfaces are described as having constant zero mean curvature instead of constant Gaussian curvature. The Sudanese Möbius strip was constructed as a minimal surface bounded by a great circle in a 3-sphere, but there is also a unique complete (boundaryless) minimal surface immersed in Euclidean space that has the topology of an open Möbius strip. It is called the Meeks Möbius strip, after its 1982 description by William Hamilton Meeks, III. Although globally unstable as a minimal surface, small patches of it, bounded by non-contractible curves within the surface, can form stable embedded Möbius strips as minimal surfaces. Both the Meeks Möbius strip, and every higher-dimensional minimal surface with the topology of the Möbius strip, can be constructed using solutions to the Björling problem, which defines a minimal surface uniquely from its boundary curve and tangent planes along this curve.

Spaces of lines

The family of lines in the plane can be given the structure of a smooth space, with each line represented as a point in this space. The resulting space of lines is topologically equivalent to the open Möbius strip. One way to see this is to extend the Euclidean plane to the real projective plane by adding one more line, the line at infinity. By projective duality the space of lines in the projective plane is equivalent to its space of points, the projective plane itself. Removing the line at infinity, to produce the space of Euclidean lines, punctures this space of projective lines. Therefore, the space of Euclidean lines is a punctured projective plane, which is one of the forms of the open Möbius strip. The space of lines in the hyperbolic plane can be parameterized by unordered pairs of distinct points on a circle, the pairs of points at infinity of each line. This space, again, has the topology of an open Möbius strip.

These spaces of lines are highly symmetric. The symmetries of Euclidean lines include the affine transformations, and the symmetries of hyperbolic lines include the Möbius transformations. The affine transformations and Möbius transformations both form 6-dimensional Lie groups, topological spaces having a compatible algebraic structure describing the composition of symmetries. Because every line in the plane is symmetric to every other line, the open Möbius strip is a homogeneous space, a space with symmetries that take every point to every other point. Homogeneous spaces of Lie groups are called solvmanifolds, and the Möbius strip can be used as a counterexample, showing that not every solvmanifold is a nilmanifold, and that not every solvmanifold can be factored into a direct product of a compact solvmanifold with ${\displaystyle {\mathbb{R}}^n}$. These symmetries also provide another way to construct the Möbius strip itself, as a group model of these Lie groups. A group model consists of a Lie group and a stabilizer subgroup of its action; contracting the cosets of the subgroup to points produces a space with the same topology as the underlying homogenous space. In the case of the symmetries of Euclidean lines, the stabilizer of the ${\displaystyle x}$-axis consists of all symmetries that take the axis to itself. Each line ${\displaystyle \ell }$ corresponds to a coset, the set of symmetries that map ${\displaystyle \ell }$ to the ${\displaystyle x}$-axis. Therefore, the quotient space, a space that has one point per coset and inherits its topology from the space of symmetries, is the same as the space of lines, and is again an open Möbius strip.

Applications

Electrical flow in a Möbius resistor

Beyond the already-discussed applications of Möbius strips to the design of mechanical belts that wear evenly on their entire surface, and of the Plücker conoid to the design of gears, other applications of Möbius strips include:

• Graphene ribbons twisted to form Möbius strips with new electronic characteristics including helical magnetism
• Möbius aromaticity, a property of organic chemicals whose molecular structure forms a cycle, with molecular orbitals aligned along the cycle in the pattern of a Möbius strip
• The Möbius resistor, a strip of conductive material covering the single side of a dielectric Möbius strip, in a way that cancels its own self-inductance
• Resonators with a compact design and a resonant frequency that is half that of identically constructed linear coils
• Polarization patterns in light emerging from a q-plate
• A proof of the impossibility of continuous, anonymous, and unanimous two-party aggregation rules in social choice theory
• Möbius loop roller coasters, a form of dual-tracked roller coaster in which the two tracks spiral around each other an odd number of times, so that the carriages return to the other track than the one they started on
• World maps projected onto a Möbius strip with the convenient properties that there are no east–west boundaries, and that the antipode of any point on the map can be found on the other printed side of the surface at the same point of the Möbius strip

Scientists have also studied the energetics of soap films shaped as Möbius strips, the chemical synthesis of molecules with a Möbius strip shape, and the formation of larger nanoscale Möbius strips using DNA origami.

In popular culture

Endless Twist, Max Bill, 1956, from the Middelheim Open Air Sculpture Museum

Two-dimensional artworks featuring the Möbius strip include an untitled 1947 painting by Corrado Cagli (memorialized in a poem by Charles Olson), and two prints by M. C. Escher: Möbius Band I (1961), depicting three folded flatfish biting each others' tails; and Möbius Band II (1963), depicting ants crawling around a lemniscate-shaped Möbius strip. It is also a popular subject of mathematical sculpture, including works by Max Bill (Endless Ribbon, 1953), José de Rivera (Infinity, 1967), and Sebastián. A trefoil-knotted Möbius strip was used in John Robinson's Immortality (1982). Charles O. Perry's Continuum (1976) is one of several pieces by Perry exploring variations of the Möbius strip.

Recycling symbol

 

Google Drive logo (2012–2014)

 

IMPA logo on stamp

Because of their easily recognized form, Möbius strips are a common element of graphic design. The familiar three-arrow logo for recycling, designed in 1970, is based on the smooth triangular form of the Möbius strip, as was the logo for the environmentally-themed Expo '74. Some variations of the recycling symbol use a different embedding with three half-twists instead of one, and the original version of the Google Drive logo used a flat-folded three-twist Möbius strip, as have other similar designs. The Brazilian Instituto Nacional de Matemática Pura e Aplicada (IMPA) uses a stylized smooth Möbius strip as their logo, and has a matching large sculpture of a Möbius strip on display in their building. The Möbius strip has also featured in the artwork for postage stamps from countries including Brazil, Belgium, the Netherlands, and Switzerland.

NASCAR Hall of Fame entrance

Möbius strips have been a frequent inspiration for the architectural design of buildings and bridges. However, many of these are projects or conceptual designs rather than constructed objects, or stretch their interpretation of the Möbius strip beyond its recognizability as a mathematical form or a functional part of the architecture. An example is the National Library of Kazakhstan, for which a building was planned in the shape of a thickened Möbius strip but refinished with a different design after the original architects pulled out of the project. One notable building incorporating a Möbius strip is the NASCAR Hall of Fame, which is surrounded by a large twisted ribbon of stainless steel acting as a façade and canopy, and evoking the curved shapes of racing tracks. On a smaller scale, Moebius Chair (2006) by Pedro Reyes is a courting bench whose base and sides have the form of a Möbius strip. As a form of mathematics and fiber arts, scarves have been knit into Möbius strips since the work of Elizabeth Zimmermann in the early 1980s. In food styling, Möbius strips have been used for slicing bagels, making loops out of bacon, and creating new shapes for pasta.

Although mathematically the Möbius strip and the fourth dimension are both purely spatial concepts, they have often been invoked in speculative fiction as the basis for a time loop into which unwary victims may become trapped. Examples of this trope include Martin Gardner's "No-Sided Professor" (1946), Armin Joseph Deutsch's "A Subway Named Mobius" (1950) and the film Moebius (1996) based on it. An entire world shaped like a Möbius strip is the setting of Arthur C. Clarke's "The Wall of Darkness" (1946), while conventional Möbius strips are used as clever inventions in multiple stories of William Hazlett Upson from the 1940s. Other works of fiction have been analyzed as having a Möbius strip–like structure, in which elements of the plot repeat with a twist; these include Marcel Proust's In Search of Lost Time (1913–1927), Luigi Pirandello's Six Characters in Search of an Author (1921), Frank Capra's It's a Wonderful Life (1946), John Barth's Lost in the Funhouse (1968), Samuel R. Delany's Dhalgren (1975) and the film Donnie Darko (2001).

One of the musical canons by J. S. Bach, the fifth of 14 canons (BWV 1087) discovered in 1974 in Bach's copy of the Goldberg Variations, features a glide-reflect symmetry in which each voice in the canon repeats, with inverted notes, the same motif from two measures earlier. Because of this symmetry, this canon can be thought of as having its score written on a Möbius strip. In music theory, tones that differ by an octave are generally considered to be equivalent notes, and the space of possible notes forms a circle, the chromatic circle. Because the Möbius strip is the configuration space of two unordered points on a circle, the space of all two-note chords takes the shape of a Möbius strip. This conception, and generalizations to more points, is a significant application of orbifolds to music theory. Modern musical groups taking their name from the Möbius strip include American electronic rock trio Mobius Band and Norwegian progressive rock band Ring Van Möbius.

Möbius strips and their properties have been used in the design of stage magic. One such trick, known as the Afghan bands, uses the fact that the Möbius strip remains in one piece as a single strip when cut lengthwise. It originated in the 1880s, and was very popular in the first half of the twentieth century. Many versions of this trick exist and have been performed by famous illusionists such as Harry Blackstone Sr. and Thomas Nelson Downs.

Knockout mouse

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Knockout_mouse 

A knockout mouse, or knock-out mouse, is a genetically modified mouse (Mus musculus) in which researchers have inactivated, or "knocked out", an existing gene by replacing it or disrupting it with an artificial piece of DNA. They are important animal models for studying the role of genes which have been sequenced but whose functions have not been determined. By causing a specific gene to be inactive in the mouse, and observing any differences from normal behaviour or physiology, researchers can infer its probable function.

Mice are currently the laboratory animal species most closely related to humans for which the knockout technique can easily be applied. They are widely used in knockout experiments, especially those investigating genetic questions that relate to human physiology. Gene knockout in rats is much harder and has only been possible since 2003.

The first recorded knockout mouse was created by Mario R. Capecchi, Martin Evans, and Oliver Smithies in 1989, for which they were awarded the 2007 Nobel Prize in Physiology or Medicine. Aspects of the technology for generating knockout mice, and the mice themselves have been patented in many countries by private companies.

Use

A laboratory mouse in which a gene affecting hair growth has been knocked out (left) is shown next to a normal lab mouse.

Knocking out the activity of a gene provides information about what that gene normally does. Humans share many genes with mice. Consequently, observing the characteristics of knockout mice gives researchers information that can be used to better understand how a similar gene may cause or contribute to disease in humans.

Examples of research in which knockout mice have been useful include studying and modeling different kinds of cancer, obesity, heart disease, diabetes, arthritis, substance abuse, anxiety, aging and Parkinson's disease. Knockout mice also offer a biological and scientific context in which drugs and other therapies can be developed and tested.

Millions of knockout mice are used in experiments each year.

Strains

A knockout mouse (left) that is a model for obesity, compared with a normal mouse

There are several thousand different strains of knockout mice. Many mouse models are named after the gene that has been inactivated. For example, the p53 knockout mouse is named after the p53 gene which codes for a protein that normally suppresses the growth of tumours by arresting cell division and/or inducing apoptosis. Humans born with mutations that deactivate the p53 gene have Li-Fraumeni syndrome, a condition that dramatically increases the risk of developing bone cancers, breast cancer and blood cancers at an early age. Other mouse models are named according to their physical characteristics or behaviours.

Procedure

The procedure for making mixed-genotype blastocyst

Breeding scheme for producing knockout mice. Blastocysts containing cells, that are both wildtype and knockout cells, are injected into the uterus of a foster mother. This produces offspring that are either wildtype and coloured the same colour as the blastocyst donor (grey) or chimera (mixed) and partially knocked out. The chimera mice are crossed with a normal wildtype mouse (grey). This produces offspring that are either white and heterozygous for the knocked out gene or grey and wildtype. White heterozygous mice can subsequently be crossed to produce mice that are homozygous for the knocked out gene.

There are several variations to the procedure of producing knockout mice; the following is a typical example.

1. The gene to be knocked out is isolated from a mouse gene library. Then a new DNA sequence is engineered which is very similar to the original gene and its immediate neighbour sequence, except that it is changed sufficiently to make the gene inoperable. Usually, the new sequence is also given a marker gene, a gene that normal mice don't have and that confers resistance to a certain toxic agent (e.g., neomycin) or that produces an observable change (e.g. colour or fluorescence). In addition, a second gene, such as herpes tk+, is also included in the construct in order to accomplish a complete selection.
2. Embryonic stem cells are isolated from a mouse blastocyst (a very young embryo) and grown in vitro. For this example, we will take stem cells from a white mouse.
3. The new sequence from step 1 is introduced into the stem cells from step 2 by electroporation. By the natural process of homologous recombination some of the electroporated stem cells will incorporate the new sequence with the knocked-out gene into their chromosomes in place of the original gene. The chances of a successful recombination event are relatively low, so the majority of altered cells will have the new sequence in only one of the two relevant chromosomes – they are said to be heterozygous. Cells that were transformed with a vector containing the neomycin resistance gene and the herpes tk+ gene are grown in a solution containing neomycin and Ganciclovir in order to select for the transformations that occurred via homologous recombination. Any insertion of DNA that occurred via random insertion will die because they test positive for both the neomycin resistance gene and the herpes tk+ gene, whose gene product reacts with Ganciclovir to produce a deadly toxin. Moreover, cells that do not integrate any of the genetic material test negative for both genes and therefore die as a result of poisoning with neomycin.
4. The embryonic stem cells that incorporated the knocked-out gene are isolated from the unaltered cells using the marker gene from step 1. For example, the unaltered cells can be killed using a toxic agent to which the altered cells are resistant.
5. The knocked-out embryonic stem cells from step 4 are inserted into a mouse blastocyst. For this example, we use blastocysts from a grey mouse. The blastocysts now contain two types of stem cells: the original ones (from the grey mouse), and the knocked-out cells (from the white mouse). These blastocysts are then implanted into the uterus of female mice, where they develop. The newborn mice will therefore be chimeras: some parts of their bodies result from the original stem cells, other parts from the knocked-out stem cells. Their fur will show patches of white and grey, with white patches derived from the knocked-out stem cells and grey patches from the recipient blastocyst.
6. Some of the newborn chimera mice will have gonads derived from knocked-out stem cells, and will therefore produce eggs or sperm containing the knocked-out gene. When these chimera mice are crossbred with others of the wild type, some of their offspring will have one copy of the knocked-out gene in all their cells. These mice do not retain any grey mouse DNA and are not chimeras, however they are still heterozygous.
7. When these heterozygous offspring are interbred, some of their offspring will inherit the knocked-out gene from both parents; they carry no functional copy of the original unaltered gene (i.e. they are homozygous for that allele).

A detailed explanation of how knockout (KO) mice are created is located at the website of the Nobel Prize in Physiology or Medicine 2007.

Limitations

The National Institutes of Health discusses some important limitations of this technique.

While knockout mouse technology represents a valuable research tool, some important limitations exist. About 15 percent of gene knockouts are developmentally lethal, which means that the genetically altered embryos cannot grow into adult mice. This problem is often overcome through the use of conditional mutations. The lack of adult mice limits studies to embryonic development and often makes it more difficult to determine a gene's function in relation to human health. In some instances, the gene may serve a different function in adults than in developing embryos.

Knocking out a gene also may fail to produce an observable change in a mouse or may even produce different characteristics from those observed in humans in which the same gene is inactivated. For example, mutations in the p53 gene are associated with more than half of human cancers and often lead to tumours in a particular set of tissues. However, when the p53 gene is knocked out in mice, the animals develop tumours in a different array of tissues.

There is variability in the whole procedure depending largely on the strain from which the stem cells have been derived. Generally cells derived from strain 129 are used. This specific strain is not suitable for many experiments (e.g., behavioural), so it is very common to backcross the offspring to other strains. Some genomic loci have been proven very difficult to knock out. Reasons might be the presence of repetitive sequences, extensive DNA methylation, or heterochromatin. The confounding presence of neighbouring 129 genes on the knockout segment of genetic material has been dubbed the "flanking-gene effect". Methods and guidelines to deal with this problem have been proposed.

Another limitation is that conventional (i.e. non-conditional) knockout mice develop in the absence of the gene being investigated. At times, loss of activity during development may mask the role of the gene in the adult state, especially if the gene is involved in numerous processes spanning development. Conditional/inducible mutation approaches are then required that first allow the mouse to develop and mature normally prior to ablation of the gene of interest.

Another serious limitation is a lack of evolutive adaptations in knockout model that might occur in wild type animals after they naturally mutate. For instance, erythrocyte-specific coexpression of GLUT1 with stomatin constitutes a compensatory mechanism in mammals that are unable to synthesize vitamin C.

Asymmetry

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Asymmetry

Asymmetry is the absence of, or a violation of, symmetry (the property of an object being invariant to a transformation, such as reflection). Symmetry is an important property of both physical and abstract systems and it may be displayed in precise terms or in more aesthetic terms. The absence of or violation of symmetry that are either expected or desired can have important consequences for a system.

In organisms

Due to how cells divide in organisms, asymmetry in organisms is fairly usual in at least one dimension, with biological symmetry also being common in at least one dimension.

Louis Pasteur proposed that biological molecules are asymmetric because the cosmic [i.e. physical] forces that preside over their formation are themselves asymmetric. While at his time, and even now, the symmetry of physical processes are highlighted, it is known that there are fundamental physical asymmetries, starting with time.

Asymmetry in biology

Main articles: Symmetry in biology and Left-right asymmetry (biology)

Asymmetry is an important and widespread trait, having evolved numerous times in many organisms and at many levels of organisation (ranging from individual cells, through organs, to entire body-shapes). Benefits of asymmetry sometimes have to do with improved spatial arrangements, such as the left human lung being smaller, and having one fewer lobes than the right lung to make room for the asymmetrical heart. In other examples, division of function between the right and left half may have been beneficial and has driven the asymmetry to become stronger. Such an explanation is usually given for mammal hand or paw preference (handedness), an asymmetry in skill development in mammals. Training the neural pathways in a skill with one hand (or paw) may take less effort than doing the same with both hands.

Nature also provides several examples of handedness in traits that are usually symmetric. The following are examples of animals with obvious left-right asymmetries:

Male fiddler crab, Uca pugnax

• Most snails, because of torsion during development, show remarkable asymmetry in the shell and in the internal organs.
• Male fiddler crabs have one big claw and one small claw.
• The narwhal's tusk is a left incisor which can grow up to 10 feet in length and forms a left-handed helix.
• Flatfish have evolved to swim with one side upward, and as a result have both eyes on one side of their heads.
• Several species of owls exhibit asymmetries in the size and positioning of their ears, which is thought to help locate prey.
• Many animals (ranging from insects to mammals) have asymmetric male genitalia. The evolutionary cause behind this is, in most cases, still a mystery.

As an indicator of unfitness

• Certain disturbances during the development of the organism, resulting in birth defects.
• Injuries after cell division that cannot be biologically repaired, such as a lost limb from an accident.

Since birth defects and injuries are likely to indicate poor health of the organism, defects resulting in asymmetry often put an animal at a disadvantage when it comes to finding a mate. For example, a greater degree of facial symmetry is seen as more attractive in humans, especially in the context of mate selection. In general, there is a correlation between symmetry and fitness-related traits such as growth rate, fecundity and survivability for many species. This means that, through sexual selection, individuals with greater symmetry (and therefore fitness) tend to be preferred as mates, as they are more likely to produce healthy offspring.

In structures

Pre-modern architectural styles tended to place an emphasis on symmetry, except where extreme site conditions or historical developments lead away from this classical ideal. To the contrary, modernist and postmodern architects became much more free to use asymmetry as a design element.

While most bridges employ a symmetrical form due to intrinsic simplicities of design, analysis and fabrication and economical use of materials, a number of modern bridges have deliberately departed from this, either in response to site-specific considerations or to create a dramatic design statement.

Some asymmetrical structures

• 
  Eastern span replacement of the San Francisco – Oakland Bay Bridge
  
  
• 
  Puente de la Mujer
  
  
• 
  Auditorio de Tenerife
  
  
• 
  Blohm & Voss BV 141 aircraft
  
  
• 
  A proa, a form of outrigger canoe

In fire protection

In fire-resistance rated wall assemblies, used in passive fire protection, including, but not limited to, high-voltage transformer fire barriers, asymmetry is a crucial aspect of design. When designing a facility, it is not always certain, that in the event of fire, which side a fire may come from. Therefore, many building codes and fire test standards outline, that a symmetrical assembly, need only be tested from one side, because both sides are the same. However, as soon as an assembly is asymmetrical, both sides must be tested and the test report is required to state the results for each side. In practical use, the lowest result achieved is the one that turns up in certification listings. Neither the test sponsor, nor the laboratory can go by an opinion or deduction as to which side was in more peril as a result of contemplated testing and then test only one side. Both must be tested in order to be compliant with test standards and building codes.

In mathematics

See also: Symmetry in mathematics

In mathematics, asymmetry can arise in various ways. Examples include asymmetric relations, asymmetry of shapes in geometry, asymmetric graphs et cetera.

Lines of symmetry

When determining whether an object is asymmetrical, look for lines of symmetry. For instance, a square has four lines of symmetry, while a circle has infinite. If a shape has no lines of symmetry, then it is asymmetrical, but if an object has any lines of symmetry, it is symmetrical.

Asymmetric Relation

An asymmetric relation is a binary relation ${\displaystyle R}$ defined on a set of elements such that if ${\displaystyle aRb}$ holds for elements ${\displaystyle a}$ and ${\displaystyle b}$, then ${\displaystyle bRa}$ must be false. Stated differently, an asymmetric relation is characterized by a necessary absence of symmetry of the relation in the opposite direction.

Inequalities exemplify asymmetric relations. Consider elements ${\displaystyle a}$ and ${\displaystyle b}$. If ${\displaystyle a}$ is less than ${\displaystyle b}$ (${\displaystyle a<b}$), then ${\displaystyle a}$ cannot be greater than ${\displaystyle b}$ (${\displaystyle a\ngtr b}$). This highlights how the relations "less than", and similarly "greater than", are not symmetric.

In contrast, if ${\displaystyle a}$ is equal to ${\displaystyle b}$ (${\displaystyle a=b}$), then ${\displaystyle b}$ is also equal to ${\displaystyle a}$ (${\displaystyle b=a}$). Thus the binary relation "equal to" is a symmetric one.

Asymmetric Tensors

In general an Asymmetric tensor is defined by the change of signs${\displaystyle (-/+)}$ of its solution under the interchange of two indexes.

The Epsilon-tensor is an example of an asymmetric tensor. It is defined as: ${\displaystyle {ϵ}_{ijk}=\{\begin{array}{ll}1& \text{if }(i,j,k)\in \{(123),(231),(312)\}\\ -1& \text{if }(i,j,k)\in \{(213),(321),(132)\}\\ 0& \text{else}\end{array}}$

,with ${\displaystyle i,j,k\in \{1,2,3\}}$. For even or uneven permutations of the indexes the tensor is either 1 or -1.

In chemistry

Certain molecules are chiral; that is, they cannot be superposed upon their mirror image. Chemically identical molecules with different chirality are called enantiomers; this difference in orientation can lead to different properties in the way they react with biological systems.

In physics

Asymmetry arises in physics in a number of different realms.

Thermodynamics

The original non-statistical formulation of thermodynamics was asymmetrical in time: it claimed that the entropy in a closed system can only increase with time. This was derived from the Second Law (either of the two, Clausius' or Lord Kelvin's statement, can be used since they are equivalent) and using the Clausius' Theorem (see Kerson Huang ISBN 978-0471815181). The later theory of statistical mechanics, however, is symmetric in time. Although it states that a system significantly below maximum entropy is very likely to evolve towards higher entropy, it also states that such a system is very likely to have evolved from higher entropy.

Particle physics

Symmetry is one of the most powerful tools in particle physics, because it has become evident that practically all laws of nature originate in symmetries. Violations of symmetry therefore present theoretical and experimental puzzles that lead to a deeper understanding of nature. Asymmetries in experimental measurements also provide powerful handles that are often relatively free from background or systematic uncertainties.

Parity violation

Main article: parity (physics)

Until the 1950s, it was believed that fundamental physics was left-right symmetric; i.e., that interactions were invariant under parity. Although parity is conserved in electromagnetism, strong interactions and gravity, it turns out to be violated in weak interactions. The Standard Model incorporates parity violation by expressing the weak interaction as a chiral gauge interaction. Only the left-handed components of particles and right-handed components of antiparticles participate in weak interactions in the Standard Model. A consequence of parity violation in particle physics is that neutrinos have only been observed as left-handed particles (and antineutrinos as right-handed particles).

In 1956–1957 Chien-Shiung Wu, E. Ambler, R. W. Hayward, D. D. Hoppes, and R. P. Hudson found a clear violation of parity conservation in the beta decay of cobalt-60. Simultaneously, R. L. Garwin, Leon Lederman, and R. Weinrich modified an existing cyclotron experiment and immediately verified parity violation.

CP violation

Main article: CP-violation

After the discovery of the violation of parity in 1956–57, it was believed that the combined symmetry of parity (P) and simultaneous charge conjugation (C), called CP, was preserved. For example, CP transforms a left-handed neutrino into a right-handed antineutrino. In 1964, however, James Cronin and Val Fitch provided clear evidence that CP symmetry was also violated in an experiment with neutral kaons.

CP violation is one of the necessary conditions for the generation of a baryon asymmetry in the early universe.

Combining the CP symmetry with simultaneous time reversal (T) produces a combined symmetry called CPT symmetry. CPT symmetry must be preserved in any Lorentz invariant local quantum field theory with a Hermitian Hamiltonian. As of 2006, no violations of CPT symmetry have been observed.

Baryon asymmetry of the universe

Main article: baryogenesis

The baryons (i.e., the protons and neutrons and the atoms that they comprise) observed so far in the universe are overwhelmingly matter as opposed to anti-matter. This asymmetry is called the baryon asymmetry of the universe.

Isospin violation

Isospin is the symmetry transformation of the weak interactions. The concept was first introduced by Werner Heisenberg in nuclear physics based on the observations that the masses of the neutron and the proton are almost identical and that the strength of the strong interaction between any pair of nucleons is the same, independent of whether they are protons or neutrons. This symmetry arises at a more fundamental level as a symmetry between up-type and down-type quarks. Isospin symmetry in the strong interactions can be considered as a subset of a larger flavor symmetry group, in which the strong interactions are invariant under interchange of different types of quarks. Including the strange quark in this scheme gives rise to the Eightfold Way scheme for classifying mesons and baryons.

Isospin is violated by the fact that the masses of the up and down quarks are different, as well as by their different electric charges. Because this violation is only a small effect in most processes that involve the strong interactions, isospin symmetry remains a useful calculational tool, and its violation introduces corrections to the isospin-symmetric results.

In collider experiments

Because the weak interactions violate parity, collider processes that can involve the weak interactions typically exhibit asymmetries in the distributions of the final-state particles. These asymmetries are typically sensitive to the difference in the interaction between particles and antiparticles, or between left-handed and right-handed particles. They can thus be used as a sensitive measurement of differences in interaction strength and/or to distinguish a small asymmetric signal from a large but symmetric background.

• A forward-backward asymmetry is defined as A_FB=(N_F-N_B)/(N_F+N_B), where N_F is the number of events in which some particular final-state particle is moving "forward" with respect to some chosen direction (e.g., a final-state electron moving in the same direction as the initial-state electron beam in electron-positron collisions), while N_B is the number of events with the final-state particle moving "backward". Forward-backward asymmetries were used by the LEP experiments to measure the difference in the interaction strength of the Z boson between left-handed and right-handed fermions, which provides a precision measurement of the weak mixing angle.
• A left-right asymmetry is defined as A_LR=(N_L-N_R)/(N_L+N_R), where N_L is the number of events in which some initial- or final-state particle is left-polarized, while N_R is the corresponding number of right-polarized events. Left-right asymmetries in Z boson production and decay were measured at the Stanford Linear Collider using the event rates obtained with left-polarized versus right-polarized initial electron beams. Left-right asymmetries can also be defined as asymmetries in the polarization of final-state particles whose polarizations can be measured; e.g., tau leptons.
• A charge asymmetry or particle-antiparticle asymmetry is defined in a similar way. This type of asymmetry has been used to constrain the parton distribution functions of protons at the Tevatron from events in which a produced W boson decays to a charged lepton. The asymmetry between positively and negatively charged leptons as a function of the direction of the W boson relative to the proton beam provides information on the relative distributions of up and down quarks in the proton. Particle-antiparticle asymmetries are also used to extract measurements of CP violation from B meson and anti-B meson production at the BaBar and Belle experiments.