From Wikipedia, the free encyclopedia
A molecular vibration occurs when atoms in a molecule are in periodic motion while the molecule as a whole has constant translational and rotational motion. The frequency of the periodic motion is known as a vibration frequency, and the typical frequencies of molecular vibrations range from less than 1012 to approximately 1014 Hz.
In general, a molecule with N atoms has 3N – 6 normal modes of vibration, but a linear molecule has 3N – 5 such modes, as rotation about its molecular axis cannot be observed.[1] A diatomic molecule has one normal mode of vibration. The normal modes of vibration of polyatomic molecules are independent of each other but each normal mode will involve simultaneous vibrations of different parts of the molecule such as different chemical bonds.
A molecular vibration is excited when the molecule absorbs a quantum of energy, E, corresponding to the vibration's frequency, ν, according to the relation E = hν (where h is Planck's constant). A fundamental vibration is excited when one such quantum of energy is absorbed by the molecule in its ground state. When two quanta are absorbed the first overtone is excited, and so on to higher overtones.
To a first approximation, the motion in a normal vibration can be described as a kind of simple harmonic motion. In this approximation, the vibrational energy is a quadratic function (parabola) with respect to the atomic displacements and the first overtone has twice the frequency of the fundamental. In reality, vibrations are anharmonic and the first overtone has a frequency that is slightly lower than twice that of the fundamental. Excitation of the higher overtones involves progressively less and less additional energy and eventually leads to dissociation of the molecule, as the potential energy of the molecule is more like a Morse potential.
The vibrational states of a molecule can be probed in a variety of ways. The most direct way is through infrared spectroscopy, as vibrational transitions typically require an amount of energy that corresponds to the infrared region of the spectrum. Raman spectroscopy, which typically uses visible light, can also be used to measure vibration frequencies directly. The two techniques are complementary and comparison between the two can provide useful structural information such as in the case of the rule of mutual exclusion for centrosymmetric molecules.
Vibrational excitation can occur in conjunction with electronic excitation (vibronic transition), giving vibrational fine structure to electronic transitions, particularly with molecules in the gas state.
Simultaneous excitation of a vibration and rotations gives rise to vibration-rotation spectra
In ethene there are 12 internal coordinates: 4 C-H stretching, 1 C-C stretching, 2 H-C-H bending, 2 CH2 rocking, 2 CH2 wagging, 1 twisting. Note that the H-C-C angles cannot be used as internal coordinates as the angles at each carbon atom cannot all increase at the same time.
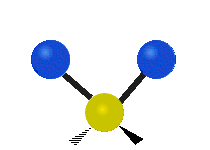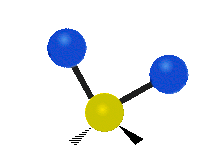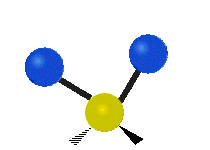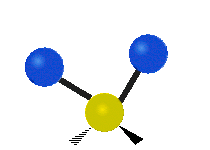
Vibrations of a methylene group (-CH2-) in a molecule for illustration
The atoms in a CH2 group, commonly found in organic compounds, can vibrate in six different ways: symmetric and asymmetric stretching, scissoring, rocking, wagging and twisting as shown here:
(These figures do not represent the "recoil" of the C atoms, which, though necessarily present to balance the overall movements of the molecule, are much smaller than the movements of the lighter H atoms).
Symmetry-adapted coordinates
Symmetry-adapted coordinates may be created by applying a projection operator to a set of internal coordinates.[2] The projection operator is constructed with the aid of the character table of the molecular point group. For example, the four(un-normalised) C-H stretching coordinates of the molecule ethene are given by
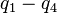 are the internal coordinates for stretching of each of the four C-H bonds.
are the internal coordinates for stretching of each of the four C-H bonds.
Illustrations of symmetry-adapted coordinates for most small molecules can be found in Nakamoto.[3]
Newtonian mechanics
Perhaps surprisingly, molecular vibrations can be treated using Newtonian mechanics to calculate the correct vibration frequencies. The basic assumption is that each vibration can be treated as though it corresponds to a spring. In the harmonic approximation the spring obeys Hooke's law: the force required to extend the spring is proportional to the extension. The proportionality constant is known as a force constant, k. The anharmonic oscillator is considered elsewhere.[5]
The difference in energy when n (or v) changes by 1 is therefore equal to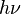 , the product of the Planck constant and the vibration frequency derived using classical mechanics. For a transition from level n to level n+1 due to absorption of a photon, the frequency of the photon is equal to the classical vibration frequency
, the product of the Planck constant and the vibration frequency derived using classical mechanics. For a transition from level n to level n+1 due to absorption of a photon, the frequency of the photon is equal to the classical vibration frequency  (in the harmonic oscillator approximation).
(in the harmonic oscillator approximation).
See quantum harmonic oscillator for graphs of the first 5 wave functions, which allow certain selection rules to be formulated. For example, for a harmonic oscillator transitions are allowed only when the quantum number n changes by one,
In general, a molecule with N atoms has 3N – 6 normal modes of vibration, but a linear molecule has 3N – 5 such modes, as rotation about its molecular axis cannot be observed.[1] A diatomic molecule has one normal mode of vibration. The normal modes of vibration of polyatomic molecules are independent of each other but each normal mode will involve simultaneous vibrations of different parts of the molecule such as different chemical bonds.
A molecular vibration is excited when the molecule absorbs a quantum of energy, E, corresponding to the vibration's frequency, ν, according to the relation E = hν (where h is Planck's constant). A fundamental vibration is excited when one such quantum of energy is absorbed by the molecule in its ground state. When two quanta are absorbed the first overtone is excited, and so on to higher overtones.
To a first approximation, the motion in a normal vibration can be described as a kind of simple harmonic motion. In this approximation, the vibrational energy is a quadratic function (parabola) with respect to the atomic displacements and the first overtone has twice the frequency of the fundamental. In reality, vibrations are anharmonic and the first overtone has a frequency that is slightly lower than twice that of the fundamental. Excitation of the higher overtones involves progressively less and less additional energy and eventually leads to dissociation of the molecule, as the potential energy of the molecule is more like a Morse potential.
The vibrational states of a molecule can be probed in a variety of ways. The most direct way is through infrared spectroscopy, as vibrational transitions typically require an amount of energy that corresponds to the infrared region of the spectrum. Raman spectroscopy, which typically uses visible light, can also be used to measure vibration frequencies directly. The two techniques are complementary and comparison between the two can provide useful structural information such as in the case of the rule of mutual exclusion for centrosymmetric molecules.
Vibrational excitation can occur in conjunction with electronic excitation (vibronic transition), giving vibrational fine structure to electronic transitions, particularly with molecules in the gas state.
Simultaneous excitation of a vibration and rotations gives rise to vibration-rotation spectra
Vibrational coordinates
The coordinate of a normal vibration is a combination of changes in the positions of atoms in the molecule. When the vibration is excited the coordinate changes sinusoidally with a frequency ν, the frequency of the vibration.Internal coordinates
Internal coordinates are of the following types, illustrated with reference to the planar molecule ethylene,- Stretching: a change in the length of a bond, such as C-H or C-C
- Bending: a change in the angle between two bonds, such as the HCH angle in a methylene group
- Rocking: a change in angle between a group of atoms, such as a methylene group and the rest of the molecule.
- Wagging: a change in angle between the plane of a group of atoms, such as a methylene group and a plane through the rest of the molecule,
- Twisting: a change in the angle between the planes of two groups of atoms, such as a change in the angle between the two methylene groups.
- Out-of-plane: a change in the angle between any one of the C-H bonds and the plane defined by the remaining atoms of the ethylene molecule. Another example is in BF3 when the boron atom moves in and out of the plane of the three fluorine atoms.
In ethene there are 12 internal coordinates: 4 C-H stretching, 1 C-C stretching, 2 H-C-H bending, 2 CH2 rocking, 2 CH2 wagging, 1 twisting. Note that the H-C-C angles cannot be used as internal coordinates as the angles at each carbon atom cannot all increase at the same time.
Vibrations of a methylene group (-CH2-) in a molecule for illustration
The atoms in a CH2 group, commonly found in organic compounds, can vibrate in six different ways: symmetric and asymmetric stretching, scissoring, rocking, wagging and twisting as shown here:| Symmetrical stretching |
Asymmetrical stretching |
Scissoring (Bending) |
|---|---|---|
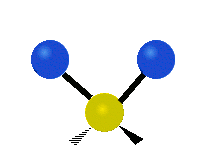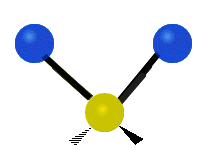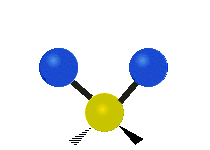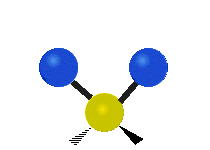 |
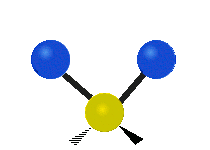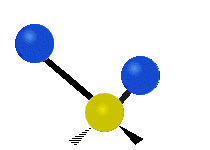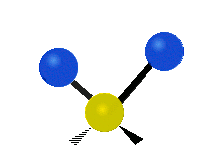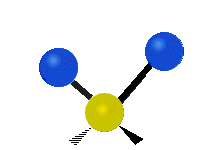 |
 |
| Rocking | Wagging | Twisting |
 |
 |
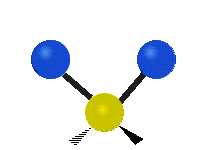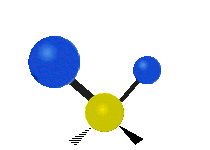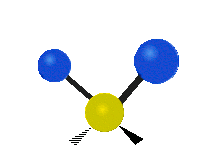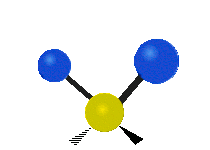 |
(These figures do not represent the "recoil" of the C atoms, which, though necessarily present to balance the overall movements of the molecule, are much smaller than the movements of the lighter H atoms).
Symmetry-adapted coordinates
Symmetry-adapted coordinates may be created by applying a projection operator to a set of internal coordinates.[2] The projection operator is constructed with the aid of the character table of the molecular point group. For example, the four(un-normalised) C-H stretching coordinates of the molecule ethene are given by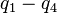 are the internal coordinates for stretching of each of the four C-H bonds.
are the internal coordinates for stretching of each of the four C-H bonds.Illustrations of symmetry-adapted coordinates for most small molecules can be found in Nakamoto.[3]
Normal coordinates
The normal coordinates, denoted as Q, refer to the positions of atoms away from their equilibrium positions, with respect to a normal mode of vibration. Each normal mode is assigned a single normal coordinate, and so the normal coordinate refers to the "progress" along that normal mode at any given time. Formally, normal modes are determined by solving a secular determinant, and then the normal coordinates (over the normal modes) can be expressed as a summation over the cartesian coordinates (over the atom positions). The advantage of working in normal modes is that they diagonalize the matrix governing the molecular vibrations, so each normal mode is an independent molecular vibration, associated with its own spectrum of quantum mechanical states. If the molecule possesses symmetries, it will belong to a point group, and the normal modes will "transform as" an irreducible representation under that group. The normal modes can then be qualitatively determined by applying group theory and projecting the irreducible representation onto the cartesian coordinates. For example, when this treatment is applied to CO2, it is found that the C=O stretches are not independent, but rather there is an O=C=O symmetric stretch and an O=C=O asymmetric stretch.- symmetric stretching: the sum of the two C-O stretching coordinates; the two C-O bond lengths change by the same amount and the carbon atom is stationary. Q = q1 + q2
- asymmetric stretching: the difference of the two C-O stretching coordinates; one C-O bond length increases while the other decreases. Q = q1 - q2
- principally C-H stretching with a little C-N stretching; Q1 = q1 + a q2 (a << 1)
- principally C-N stretching with a little C-H stretching; Q2 = b q1 + q2 (b << 1)
Newtonian mechanics

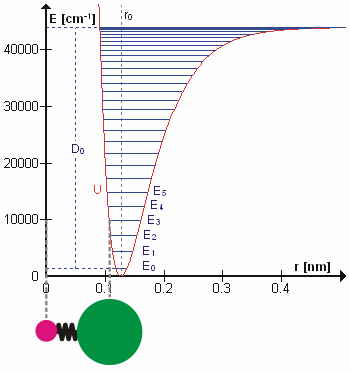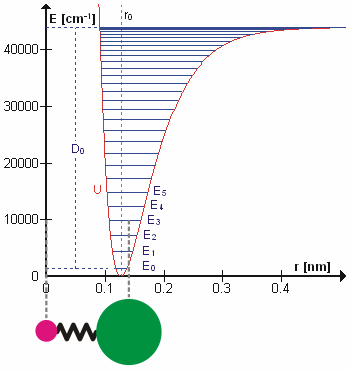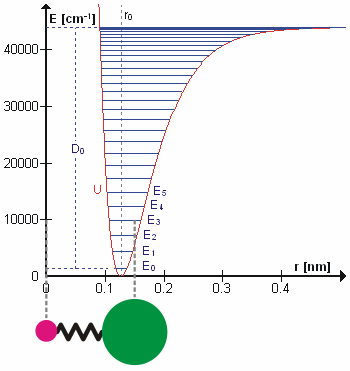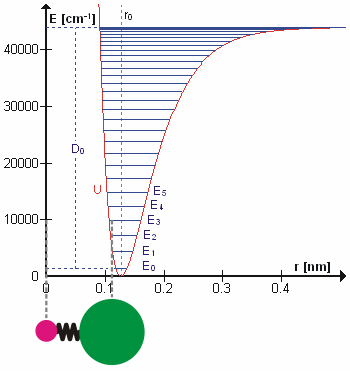
The HCl molecule as an anharmonic oscillator vibrating at energy level E3. D0 is dissociation energy here, r0 bond length, U potential energy. Energy is expressed in wavenumbers. The hydrogen chloride molecule is attached to the coordinate system to show bond length changes on the curve.
Perhaps surprisingly, molecular vibrations can be treated using Newtonian mechanics to calculate the correct vibration frequencies. The basic assumption is that each vibration can be treated as though it corresponds to a spring. In the harmonic approximation the spring obeys Hooke's law: the force required to extend the spring is proportional to the extension. The proportionality constant is known as a force constant, k. The anharmonic oscillator is considered elsewhere.[5]
Quantum mechanics
In the harmonic approximation the potential energy is a quadratic function of the normal coordinates. Solving the Schrödinger wave equation, the energy states for each normal coordinate are given by ,
,
The difference in energy when n (or v) changes by 1 is therefore equal to
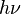 , the product of the Planck constant and the vibration frequency derived using classical mechanics. For a transition from level n to level n+1 due to absorption of a photon, the frequency of the photon is equal to the classical vibration frequency
, the product of the Planck constant and the vibration frequency derived using classical mechanics. For a transition from level n to level n+1 due to absorption of a photon, the frequency of the photon is equal to the classical vibration frequency  (in the harmonic oscillator approximation).
(in the harmonic oscillator approximation).See quantum harmonic oscillator for graphs of the first 5 wave functions, which allow certain selection rules to be formulated. For example, for a harmonic oscillator transitions are allowed only when the quantum number n changes by one,











 ,
,























