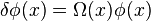In
physics, a
symmetry of a
physical system is a physical or mathematical feature of the system (observed or intrinsic) that is preserved or remains unchanged under some transformation.
A family of particular transformations may be
continuous (such as
rotation of a circle) or
discrete (e.g.,
reflection of a bilaterally symmetric figure, or rotation of a regular polygon). Continuous and discrete transformations give rise to corresponding types of symmetries. Continuous symmetries can be described by
Lie groups while discrete symmetries are described by finite groups (see
Symmetry group). Symmetries are frequently amenable to mathematical formulations such as
group representations and can be exploited to simplify many problems.
An important example of such symmetry is the
invariance of the form of physical laws under arbitrary differentiable coordinate transformations.
Symmetry as invariance
Invariance is specified mathematically by transformations that leave some quantity unchanged. This idea can apply to basic real-world observations. For example,
temperature may be constant throughout a room. Since the temperature is independent of position within the room, the temperature is
invariant under a shift in the measurer's position.
Similarly, a uniform sphere rotated about its center will appear exactly as it did before the rotation. The sphere is said to exhibit
spherical symmetry. A rotation about any
axis of the sphere will preserve how the sphere "looks".
Invariance in force
The above ideas lead to the useful idea of
invariance when discussing observed physical symmetry; this can be applied to symmetries in forces as well.
For example, an electric field due to a wire is said to exhibit
cylindrical symmetry, because the
electric field strength at a given distance
r from the electrically charged wire of infinite length will have the same magnitude at each point on the surface of a cylinder (whose axis is the wire) with radius
r. Rotating the wire about its own axis does not change its position or charge density, hence it will preserve the field. The field strength at a rotated position is the same. Suppose some configuration of charges (may be non-stationary) produce an electric field in some direction, then rotating the configuration of the charges (without disturbing the internal dynamics that produces the particular field) will lead to a net rotation of the direction of the electric field. These two properties are interconnected through the more general property that rotating
any system of charges causes a corresponding rotation of the electric field.
In Newton's theory of mechanics, given two bodies, each with mass
m, starting from rest at the origin and moving along the
x-axis in opposite directions, one with speed
v1 and the other with speed
v2 the total
kinetic energy of the system (as calculated from an observer at the origin) is
1⁄2m(v12 + v22) and remains the same if the velocities are interchanged. The total kinetic energy is preserved under a reflection in the
y-axis.
The last example above illustrates another way of expressing symmetries, namely through the equations that describe some aspect of the physical system. The above example shows that the total kinetic energy will be the same if
v1 and
v2 are interchanged.
Local and global symmetries
Symmetries may be broadly classified as
global or
local. A
global symmetry is one that holds at all points of
spacetime, whereas a
local symmetry is one that has a different symmetry transformation at different points of
spacetime; specifically a local symmetry transformation is parameterised by the spacetime co-ordinates. Local symmetries play an important role in physics as they form the basis for
gauge theories.
Continuous symmetries
The two examples of rotational symmetry described above - spherical and cylindrical - are each instances of
continuous symmetry. These are characterised by invariance following a continuous change in the geometry of the system. For example, the wire may be rotated through any angle about its axis and the field strength will be the same on a given cylinder. Mathematically, continuous symmetries are described by
continuous or
smooth functions. An important subclass of continuous symmetries in physics are spacetime symmetries.
Spacetime symmetries
Continuous
spacetime symmetries are symmetries involving transformations of
space and
time. These may be further classified as
spatial symmetries, involving only the spatial geometry associated with a physical system;
temporal symmetries, involving only changes in time; or
spatio-temporal symmetries, involving changes in both space and time.
- Time translation: A physical system may have the same features over a certain interval of time
 ; this is expressed mathematically as invariance under the transformation
; this is expressed mathematically as invariance under the transformation  for any real numbers t and a in the interval. For example, in classical mechanics, a particle solely acted upon by gravity will have gravitational potential energy
for any real numbers t and a in the interval. For example, in classical mechanics, a particle solely acted upon by gravity will have gravitational potential energy  when suspended from a height
when suspended from a height 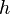 above the Earth's surface. Assuming no change in the height of the particle, this will be the total gravitational potential energy of the particle at all times. In other words, by considering the state of the particle at some time (in seconds)
above the Earth's surface. Assuming no change in the height of the particle, this will be the total gravitational potential energy of the particle at all times. In other words, by considering the state of the particle at some time (in seconds) 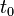 and also at
and also at  , say, the particle's total gravitational potential energy will be preserved.
, say, the particle's total gravitational potential energy will be preserved.
- Spatial translation: These spatial symmetries are represented by transformations of the form
 and describe those situations where a property of the system does not change with a continuous change in location. For example, the temperature in a room may be independent of where the thermometer is located in the room.
and describe those situations where a property of the system does not change with a continuous change in location. For example, the temperature in a room may be independent of where the thermometer is located in the room.
- Spatial rotation: These spatial symmetries are classified as proper rotations and improper rotations. The former are just the 'ordinary' rotations; mathematically, they are represented by square matrices with unit determinant. The latter are represented by square matrices with determinant −1 and consist of a proper rotation combined with a spatial reflection (inversion). For example, a sphere has proper rotational symmetry. Other types of spatial rotations are described in the article Rotation symmetry.
- Inversion transformations: These are spatio-temporal symmetries which generalise Poincaré transformations to include other conformal one-to-one transformations on the space-time coordinates. Lengths are not invariant under inversion transformations but there is a cross-ratio on four points that is invariant.
Mathematically, spacetime symmetries are usually described by
smooth vector fields on a
smooth manifold. The underlying
local diffeomorphisms associated with the vector fields correspond more directly to the physical symmetries, but the vector fields themselves are more often used when classifying the symmetries of the physical system.
Some of the most important vector fields are
Killing vector fields which are those spacetime symmetries that preserve the underlying
metric structure of a manifold. In rough terms, Killing vector fields preserve the distance between any two points of the manifold and often go by the name of
isometries.
Discrete symmetries
A
discrete symmetry is a symmetry that describes non-continuous changes in a system. For example, a square possesses discrete rotational symmetry, as only rotations by multiples of right angles will preserve the square's original appearance. Discrete symmetries sometimes involve some type of 'swapping', these swaps usually being called
reflections or
interchanges.
- Time reversal: Many laws of physics describe real phenomena when the direction of time is reversed. Mathematically, this is represented by the transformation,
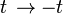 . For example, Newton's second law of motion still holds if, in the equation
. For example, Newton's second law of motion still holds if, in the equation  ,
, 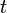 is replaced by
is replaced by  . This may be illustrated by recording the motion of an object thrown up vertically (neglecting air resistance) and then playing it back. The object will follow the same parabolic trajectory through the air, whether the recording is played normally or in reverse. Thus, position is symmetric with respect to the instant that the object is at its maximum height.
. This may be illustrated by recording the motion of an object thrown up vertically (neglecting air resistance) and then playing it back. The object will follow the same parabolic trajectory through the air, whether the recording is played normally or in reverse. Thus, position is symmetric with respect to the instant that the object is at its maximum height.
- Spatial inversion: These are represented by transformations of the form
 and indicate an invariance property of a system when the coordinates are 'inverted'. Said another way, these are symmetries between a certain object and its mirror image.
and indicate an invariance property of a system when the coordinates are 'inverted'. Said another way, these are symmetries between a certain object and its mirror image.
C, P, and T symmetries
The
Standard model of
particle physics has three related natural near-symmetries. These state that the actual universe about us is indistinguishable from one where:
T-symmetry is counterintuitive (surely the future and the past are not symmetrical) but explained by the fact that the
Standard model describes local properties, not global ones like
entropy. To properly reverse the direction of time, one would have to put the
big bang and the resulting low-
entropy state in the "future." Since we perceive the "past" ("future") as having lower (higher) entropy than the present (see
perception of time), the inhabitants of this hypothetical time-reversed universe would perceive the future in the same way as we perceive the past.
These symmetries are near-symmetries because each is broken in the present-day universe. However, the
Standard Model predicts that the combination of the three (that is, the simultaneous application of all three transformations) must be a symmetry, called
CPT symmetry.
CP violation, the violation of the combination of C- and P-symmetry, is necessary for the presence of significant amounts of
baryonic matter in the universe. CP violation is a fruitful area of current research in
particle physics.
Supersymmetry
A type of symmetry known as supersymmetry has been used to try to make theoretical advances in the
standard model. Supersymmetry is based on the idea that there is another physical symmetry beyond those already developed in the standard model, specifically a symmetry between
bosons and
fermions. Supersymmetry asserts that each type of boson has, as a supersymmetric partner, a fermion, called a superpartner, and vice versa. Supersymmetry has not yet been experimentally verified: no known particle has the correct properties to be a superpartner of any other known particle. If superpartners exist they must have masses greater than current
particle accelerators can generate.
Mathematics of physical symmetry
The transformations describing physical symmetries typically form a mathematical
group.
Group theory is an important area of mathematics for physicists.
Continuous symmetries are specified mathematically by
continuous groups (called
Lie groups). Many physical symmetries are isometries and are specified by symmetry groups. Sometimes this term is used for more general types of symmetries. The set of all proper rotations (about any angle) through any axis of a sphere form a Lie group called the
special orthogonal group 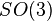
. (The
3 refers to the three-dimensional space of an ordinary sphere.) Thus, the symmetry group of the sphere with proper rotations is
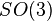
. Any rotation preserves distances on the surface of the ball. The set of all Lorentz transformations form a group called the
Lorentz group (this may be generalised to the
Poincaré group).
Discrete symmetries are described by discrete groups. For example, the symmetries of an equilateral triangle are described by the
symmetric group 
.
An important type of physical theory based on
local symmetries is called a
gauge theory and the symmetries natural to such a theory are called
gauge symmetries. Gauge symmetries in the
Standard model, used to describe three of the
fundamental interactions, are based on the
SU(3) × SU(2) × U(1) group. (Roughly speaking, the symmetries of the SU(3) group describe the
strong force, the SU(2) group describes the
weak interaction and the U(1) group describes the
electromagnetic force.)
Also, the reduction by symmetry of the energy functional under the action by a group and
spontaneous symmetry breaking of transformations of symmetric groups appear to elucidate topics in
particle physics (for example, the unification of
electromagnetism and the
weak force in
physical cosmology).
Conservation laws and symmetry
The symmetry properties of a physical system are intimately related to the
conservation laws characterizing that system.
Noether's theorem gives a precise description of this relation. The theorem states that each continuous symmetry of a physical system implies that some physical property of that system is conserved. Conversely, each conserved quantity has a corresponding symmetry. For example, the
isometry of
space gives rise to
conservation of (linear) momentum, and
isometry of
time gives rise to
conservation of energy.
The following table summarizes some fundamental symmetries and the associated conserved quantity.
Mathematics
Continuous symmetries in physics preserve transformations. One can specify a symmetry by showing how a very small transformation affects various
particle fields. The
commutator of two of these infinitessimal transformations are equivalent to a third infinitessimal transformation of the same kind hence they form a
Lie algebra.
A general coordinate transformation (also known as a
diffeomorphism) has the infinitessimal effect on a
scalar,
spinor and
vector field for example:


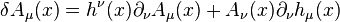
for a general field,
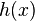
. Without gravity only the Poincaré symmetries are preserved which restricts
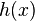
to be of the form:

where
M is an antisymmetric
matrix (giving the Lorentz and rotational symmetries) and
P is a general vector (giving the translational symmetries). Other symmetries affect multiple fields simultaneously. For example local gauge transformations apply to both a vector and spinor field:

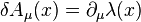
where

are generators of a particular
Lie group. So far the transformations on the right have only included fields of the same type. Supersymmetries are defined according to how the mix fields of
different types.
Another symmetry which is part of some theories of physics and not in others is scale invariance which involve Weyl transformations of the following kind:
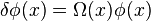
If the fields have this symmetry then it can be shown that the field theory is almost certainly conformally invariant also. This means that in the absence of gravity h(x) would restricted to the form:

with
D generating scale transformations and
K generating special conformal transformations. For example N=4 super-
Yang-Mills theory has this symmetry while
General Relativity doesn't although other theories of gravity such as
conformal gravity do. The 'action' of a field theory is an
invariant under all the symmetries of the theory. Much of modern theoretical physics is to do with speculating on the various symmetries the Universe may have and finding the invariants to construct field theories as models.
In string theories, since a string can be decomposed into an infinite number of particle fields, the symmetries on the string world sheet is equivalent to special transformations which mix an infinite number of fields.
 denotes the scalar product, ∇ is the nabla operator, here indicating a gradient, and a(y) is a vector of current coefficients, analogously corresponding to the divergence of a vector c.d. associated to the c.q. j(y):
denotes the scalar product, ∇ is the nabla operator, here indicating a gradient, and a(y) is a vector of current coefficients, analogously corresponding to the divergence of a vector c.d. associated to the c.q. j(y): denotes the tensor product.
denotes the tensor product.


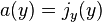


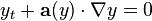

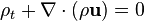



![\begin{align}
\nabla\cdot \bold u=0\\[1.2ex]
{\partial \bold u \over\partial t}+ \bold u \cdot
\nabla \bold u + \nabla s =\bold{0},
\end{align}](http://upload.wikimedia.org/math/a/4/1/a41d09db32351822a7dd7fe6894f70b3.png)

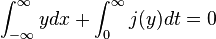
![\oint [y d^N r + j (y) dt] = 0](http://upload.wikimedia.org/math/9/b/d/9bd67a8cf940330a64d21f319ff0f240.png)

 ; this is expressed mathematically as invariance under the transformation
; this is expressed mathematically as invariance under the transformation  for any
for any  when suspended from a height
when suspended from a height 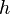 above the Earth's surface. Assuming no change in the height of the particle, this will be the total gravitational potential energy of the particle at all times. In other words, by considering the state of the particle at some time (in seconds)
above the Earth's surface. Assuming no change in the height of the particle, this will be the total gravitational potential energy of the particle at all times. In other words, by considering the state of the particle at some time (in seconds) 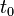 and also at
and also at  , say, the particle's total gravitational potential energy will be preserved.
, say, the particle's total gravitational potential energy will be preserved. and describe those situations where a property of the system does not change with a continuous change in location. For example, the temperature in a room may be independent of where the thermometer is located in the room.
and describe those situations where a property of the system does not change with a continuous change in location. For example, the temperature in a room may be independent of where the thermometer is located in the room.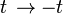 . For example,
. For example,  ,
, 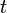 is replaced by
is replaced by  . This may be illustrated by recording the motion of an object thrown up vertically (neglecting air resistance) and then playing it back. The object will follow the same
. This may be illustrated by recording the motion of an object thrown up vertically (neglecting air resistance) and then playing it back. The object will follow the same  and indicate an invariance property of a system when the coordinates are 'inverted'. Said another way, these are symmetries between a certain object and its
and indicate an invariance property of a system when the coordinates are 'inverted'. Said another way, these are symmetries between a certain object and its 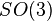 . (The 3 refers to the three-dimensional space of an ordinary sphere.) Thus, the symmetry group of the sphere with proper rotations is
. (The 3 refers to the three-dimensional space of an ordinary sphere.) Thus, the symmetry group of the sphere with proper rotations is  .
.

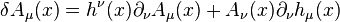
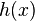 . Without gravity only the Poincaré symmetries are preserved which restricts
. Without gravity only the Poincaré symmetries are preserved which restricts 

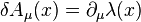
 are generators of a particular
are generators of a particular