From Wikipedia, the free encyclopedia
A conservation law is a system of homogeneous first-order quasilinear hyperbolic equation that (in one space dimension) can be put into the form:[1]
In mathematical physics, conservation equations express a particular measurable property of an isolated physical system does not change as the system evolves. One particularly important result concerning conservation equations is Noether's theorem, which states that there is a one-to-one correspondence between each one of them and a differentiable symmetry in the system. For example, the conservation of energy follows from the time-invariance of physical systems, and the fact that physical systems behave the same regardless of how they are oriented in space gives rise to the conservation of angular momentum.
Differential forms
In the one-dimensional space a conservation equation is a first-order quasilinear hyperbolic equation that can be put into the advection form: denotes the scalar product, ∇ is the nabla operator, here indicating a gradient, and a(y) is a vector of current coefficients, analogously corresponding to the divergence of a vector c.d. associated to the c.q. j(y):
denotes the scalar product, ∇ is the nabla operator, here indicating a gradient, and a(y) is a vector of current coefficients, analogously corresponding to the divergence of a vector c.d. associated to the c.q. j(y):In the general case a conservation equation can be also a system of this kind of equations (a vector equation) in the form:[1]
- u is the flow velocity vector, with components in a N-dimensional space u1, u2 ... uN,
- s is the specific pressure (pressure per unit density) giving the source term,
 denotes the tensor product.
denotes the tensor product.Integral and weak forms
Conservation equations can be also expressed in integral form: the advantage of the latter is substantially that it requires less smoothness of the solution, which paves the way to weak form, extending the class of admissible solutions to include discontinuous solutions.[2] By integrating in any space-time domain the current density form in 1-D space:Moreover, by defining a test function φ(r,t) continuously differentiable both in time and space with compact support, the weak form can be obtained pivoting on the initial condition. In 1-D space it is:
Exact laws
A partial listing of physical conservation equations due to symmetry that are said to be exact laws, or more precisely have never been [proven to be] violated:| Conservation Law | Respective Noether symmetry invariance | Number of dimensions | ||
|---|---|---|---|---|
| Conservation of mass-energy | Time invariance | Lorentz invariance symmetry | 1 | translation about time axis |
| Conservation of linear momentum | Galilean invariance | 3 | translation about x,y,z position | |
| Conservation of angular momentum | Rotation invariance | 3 | rotation about x,y,z axes | |
| CPT symmetry (combining charge, parity and time conjugation) | Lorentz invariance | 1+1+1 | (charge inversion q→-q) + (position inversion r→-r) + (time inversion t→-t) | |
| Conservation of electric charge | Gauge invariance | 1⊗4 | scalar field (1D) in 4D spacetime (x,y,z + time evolution) | |
| Conservation of color charge | SU(3) Gauge invariance | 3 | r,g,b | |
| Conservation of weak isospin | SU(2)L Gauge invariance | 1 | weak charge | |
| Conservation of probability | Probability invariance | 1⊗4 | total probability always=1 in whole x,y,z space, during time evolution | |
Approximate laws
There are also approximate conservation laws. These are approximately true in particular situations, such as low speeds, short time scales, or certain interactions.- Conservation of mass (applies for non-relativistic speeds and when there are no nuclear reactions)
- Conservation of baryon number (See chiral anomaly)
- Conservation of lepton number (In the Standard Model)
- Conservation of flavor (violated by the weak interaction)
- Conservation of parity
- Invariance under Charge conjugation
- Invariance under time reversal
- CP symmetry, the combination of charge and parity conjugation (equivalent to time reversal if CPT holds)



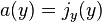


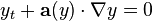

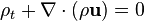



![\begin{align}
\nabla\cdot \bold u=0\\[1.2ex]
{\partial \bold u \over\partial t}+ \bold u \cdot
\nabla \bold u + \nabla s =\bold{0},
\end{align}](http://upload.wikimedia.org/math/a/4/1/a41d09db32351822a7dd7fe6894f70b3.png)

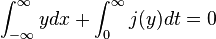
![\oint [y d^N r + j (y) dt] = 0](http://upload.wikimedia.org/math/9/b/d/9bd67a8cf940330a64d21f319ff0f240.png)

