From Wikipedia, the free encyclopedia

The quadratic formula expresses the solution of the degree two equation
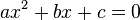 in terms of its coefficients
in terms of its coefficients 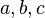 , where
, where  is not zero.
is not zero.
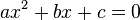 in terms of its coefficients
in terms of its coefficients 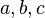 , where
, where  is not zero.
is not zero.Algebra (from Arabic al-jebr meaning "reunion of broken parts"[1]) is one of the broad parts of mathematics, together with number theory, geometry and analysis. In its most general form algebra is the study of symbols and the rules for manipulating symbols[2] and is a unifying thread of almost all of mathematics.[3] As such, it includes everything from elementary equation solving to the study of abstractions such as groups, rings, and fields. The more basic parts of algebra are called elementary algebra, the more abstract parts are called abstract algebra or modern algebra. Elementary algebra is essential for any study of mathematics, science, or engineering, as well as such applications as medicine and economics. Abstract algebra is a major area in advanced mathematics, studied primarily by professional mathematicians. Much early work in algebra, as the Arabic origin of its name suggests, was done in the Near East, by such mathematicians as Omar Khayyam (1048–1131).[4][5]
Elementary algebra differs from arithmetic in the use of abstractions, such as using letters to stand for numbers that are either unknown or allowed to take on many values.[6] For example, in
 the letter
the letter  is unknown, but the law of inverses can be used to discover its value:
is unknown, but the law of inverses can be used to discover its value: 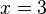 . In
. In 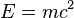 , the letters
, the letters 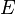 and
and 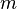 are variables, and the letter
are variables, and the letter  is a constant. Algebra gives methods for solving equations and expressing formulas that are much easier (for those who know how to use them) than the older method of writing everything out in words.
is a constant. Algebra gives methods for solving equations and expressing formulas that are much easier (for those who know how to use them) than the older method of writing everything out in words.The word algebra is also used in certain specialized ways. A special kind of mathematical object in abstract algebra is called an "algebra", and the word is used, for example, in the phrases linear algebra and algebraic topology (see below).
A mathematician who does research in algebra is called an algebraist.
Etymology
The word algebra comes from the Arabic language (الجبر al-jabr "restoration") from the title of the book Ilm al-jabr wa'l-muḳābala by al-Khwarizmi. The word entered the English language during Late Middle English from either Spanish, Italian, or Medieval Latin. Algebra originally referred to a surgical procedure, and still is used in that sense in Spanish, while the mathematical meaning was a later development.[7]Different meanings of "algebra"
The word "algebra" has several related meanings in mathematics, as a single word or with qualifiers.- As a single word without article, "algebra" names a broad part of mathematics (see below).
- As a single word with article or in plural, "algebra" denotes a specific mathematical structure. See algebra (ring theory) and algebra over a field. More generally, in universal algebra, it can refer to any structure.
- With a qualifier, there is the same distinction:
- Without article, it means a part of algebra, such as linear algebra, elementary algebra (the symbol-manipulation rules taught in elementary courses of mathematics as part of primary and secondary education), or abstract algebra (the study of the algebraic structures for themselves).
- With an article, it means an instance of some abstract structure, like a Lie algebra or an associative algebra.
- Frequently both meanings exist for the same qualifier, as in the sentence: Commutative algebra is the study of commutative rings, which are commutative algebras over the integers.
Algebra as a branch of mathematics
Algebra began with computations similar to those of arithmetic, with letters standing for numbers.[6] This allowed proofs of properties that are true no matter which numbers are involved. For example, in the quadratic equation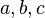 can be any numbers whatsoever (except that
can be any numbers whatsoever (except that  cannot be
cannot be  ), and the quadratic formula can be used to quickly and easily find the value of the unknown quantity
), and the quadratic formula can be used to quickly and easily find the value of the unknown quantity  .
.As it developed, algebra was extended to other non-numerical objects, such as vectors, matrices, and polynomials. Then the structural properties of these non-numerical objects were abstracted to define algebraic structures such as groups, rings, and fields.
Before the 16th century, mathematics was divided into only two subfields, arithmetic and geometry. Even though some methods, which had been developed much earlier, may be considered nowadays as algebra, the emergence of algebra and, soon thereafter, of infinitesimal calculus as subfields of mathematics only dates from 16th or 17th century. From the second half of 19th century on, many new fields of mathematics appeared, most of which made use of both arithmetic and geometry, and almost all of which used algebra.
Today, algebra has grown until it includes many branches of mathematics, as can be seen in the Mathematics Subject Classification[8] where none of the first level areas (two digit entries) is called algebra. Today algebra includes section 08-General algebraic systems, 12-Field theory and polynomials, 13-Commutative algebra, 15-Linear and multilinear algebra; matrix theory, 16-Associative rings and algebras, 17-Nonassociative rings and algebras, 18-Category theory; homological algebra, 19-K-theory and 20-Group theory. Algebra is also used extensively in 11-Number theory and 14-Algebraic geometry.
History
The start of algebra as an area of mathematics may be dated to the end of 16th century, with François Viète's work. Until the 19th century, algebra consisted essentially of the theory of equations. In the following, "Prehistory of algebra" is about the results of the theory of equations that precede the emergence of algebra as an area of mathematics.Early history of algebra
The roots of algebra can be traced to the ancient Babylonians,[9] who developed an advanced arithmetical system with which they were able to do calculations in an algorithmic fashion. The Babylonians developed formulas to calculate solutions for problems typically solved today by using linear equations, quadratic equations, and indeterminate linear equations. By contrast, most Egyptians of this era, as well as Greek and Chinese mathematics in the 1st millennium BC, usually solved such equations by geometric methods, such as those described in the Rhind Mathematical Papyrus, Euclid's Elements, and The Nine Chapters on the Mathematical Art. The geometric work of the Greeks, typified in the Elements, provided the framework for generalizing formulae beyond the solution of particular problems into more general systems of stating and solving equations, although this would not be realized until mathematics developed in medieval Islam.[10]
By the time of Plato, Greek mathematics had undergone a drastic change. The Greeks created a geometric algebra where terms were represented by sides of geometric objects, usually lines, that had letters associated with them.[6] Diophantus (3rd century AD) was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations,[11] and have led, in number theory to the modern notion of Diophantine equation.
Earlier traditions discussed above had a direct influence on Muhammad ibn Mūsā al-Khwārizmī (c. 780–850). He later wrote The Compendious Book on Calculation by Completion and Balancing, which established algebra as a mathematical discipline that is independent of geometry and arithmetic.[12]
The Hellenistic mathematicians Hero of Alexandria and Diophantus[13] as well as Indian mathematicians such as Brahmagupta continued the traditions of Egypt and Babylon, though Diophantus' Arithmetica and Brahmagupta's Brahmasphutasiddhanta are on a higher level.[14] For example, the first complete arithmetic solution (including zero and negative solutions) to quadratic equations was described by Brahmagupta in his book Brahmasphutasiddhanta. Later, Arabic and Muslim mathematicians developed algebraic methods to a much higher degree of sophistication. Although Diophantus and the Babylonians used mostly special ad hoc methods to solve equations, Al-Khwarizmi contribution was fundamental. He solved linear and quadratic equations without algebraic symbolism, negative numbers or zero, thus he has to distinguish several types of equations.[15]
In the context where algebra is identified with the theory of equations, the Greek mathematician Diophantus has traditionally been known as the "father of algebra" but in more recent times there is much debate over whether al-Khwarizmi, who founded the discipline of al-jabr, deserves that title instead.[16] Those who support Diophantus point to the fact that the algebra found in Al-Jabr is slightly more elementary than the algebra found in Arithmetica and that Arithmetica is syncopated while Al-Jabr is fully rhetorical.[17] Those who support Al-Khwarizmi point to the fact that he introduced the methods of "reduction" and "balancing" (the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation) which the term al-jabr originally referred to,[18] and that he gave an exhaustive explanation of solving quadratic equations,[19] supported by geometric proofs, while treating algebra as an independent discipline in its own right.[20] His algebra was also no longer concerned "with a series of problems to be resolved, but an exposition which starts with primitive terms in which the combinations must give all possible prototypes for equations, which henceforward explicitly constitute the true object of study". He also studied an equation for its own sake and "in a generic manner, insofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems".[21]
The Persian mathematician Omar Khayyam is credited with identifying the foundations of algebraic geometry and found the general geometric solution of the cubic equation. Another Persian mathematician, Sharaf al-Dīn al-Tūsī, found algebraic and numerical solutions to various cases of cubic equations.[22] He also developed the concept of a function.[23] The Indian mathematicians Mahavira and Bhaskara II, the Persian mathematician Al-Karaji,[24] and the Chinese mathematician Zhu Shijie, solved various cases of cubic, quartic, quintic and higher-order polynomial equations using numerical methods. In the 13th century, the solution of a cubic equation by Fibonacci is representative of the beginning of a revival in European algebra. As the Islamic world was declining, the European world was ascending. And it is here that algebra was further developed.
History of algebra

Italian mathematician Girolamo Cardano published the solutions to the cubic and quartic equations in his 1545 book Ars magna.
François Viète's work on new algebra at the close of the 16th century was an important step towards modern algebra. In 1637, René Descartes published La Géométrie, inventing analytic geometry and introducing modern algebraic notation. Another key event in the further development of algebra was the general algebraic solution of the cubic and quartic equations, developed in the mid-16th century. The idea of a determinant was developed by Japanese mathematician Kowa Seki in the 17th century, followed independently by Gottfried Leibniz ten years later, for the purpose of solving systems of simultaneous linear equations using matrices. Gabriel Cramer also did some work on matrices and determinants in the 18th century. Permutations were studied by Joseph-Louis Lagrange in his 1770 paper Réflexions sur la résolution algébrique des équations devoted to solutions of algebraic equations, in which he introduced Lagrange resolvents. Paolo Ruffini was the first person to develop the theory of permutation groups, and like his predecessors, also in the context of solving algebraic equations.
Abstract algebra was developed in the 19th century, deriving from the interest in solving equations, initially focusing on what is now called Galois theory, and on constructibility issues.[25] George Peacock was the founder of axiomatic thinking in arithmetic and algebra. Augustus De Morgan discovered relation algebra in his Syllabus of a Proposed System of Logic. Josiah Willard Gibbs developed an algebra of vectors in three-dimensional space, and Arthur Cayley developed an algebra of matrices (this is a noncommutative algebra).[26]
Areas of mathematics with the word algebra in their name
Some areas of mathematics that fall under the classification abstract algebra have the word algebra in their name; linear algebra is one example. Others do not: group theory, ring theory, and field theory are examples. In this section, we list some areas of mathematics with the word "algebra" in the name.- Elementary algebra, the part of algebra that is usually taught in elementary courses of mathematics.
- Abstract algebra, in which algebraic structures such as groups, rings and fields are axiomatically defined and investigated.
- Linear algebra, in which the specific properties of linear equations, vector spaces and matrices are studied.
- Commutative algebra, the study of commutative rings.
- Computer algebra, the implementation of algebraic methods as algorithms and computer programs.
- Homological algebra, the study of algebraic structures that are fundamental to study topological spaces.
- Universal algebra, in which properties common to all algebraic structures are studied.
- Algebraic number theory, in which the properties of numbers are studied from an algebraic point of view.
- Algebraic geometry, a branch of geometry, in its primitive form specifying curves and surfaces as solutions of polynomial equations.
- Algebraic combinatorics, in which algebraic methods are used to study combinatorial questions.
- Algebra over a field or more generally algebra over a ring.
Many classes of algebras over a field or over a ring have a specific name: - In measure theory,
- In category theory
- In logic,
- Relational algebra: a set of finitary relations that is closed under certain operators.
- Boolean algebra, a structure abstracting the computation with the truth values false and true. See also Boolean algebra (structure).
- Heyting algebra
Elementary algebra
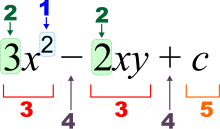
Elementary algebra is the most basic form of algebra. It is taught to students who are presumed to have no knowledge of mathematics beyond the basic principles of arithmetic. In arithmetic, only numbers and their arithmetical operations (such as +, −, ×, ÷) occur. In algebra, numbers are often represented by symbols called variables (such as a, n, x, y or z). This is useful because:
- It allows the general formulation of arithmetical laws (such as a + b = b + a for all a and b), and thus is the first step to a systematic exploration of the properties of the real number system.
- It allows the reference to "unknown" numbers, the formulation of equations and the study of how to solve these. (For instance, "Find a number x such that 3x + 1 = 10" or going a bit further "Find a number x such that ax + b = c". This step leads to the conclusion that it is not the nature of the specific numbers that allows us to solve it, but that of the operations involved.)
- It allows the formulation of functional relationships. (For instance, "If you sell x tickets, then your profit will be 3x − 10 dollars, or f(x) = 3x − 10, where f is the function, and x is the number to which the function is applied".)
Polynomials
Two important and related problems in algebra are the factorization of polynomials, that is, expressing a given polynomial as a product of other polynomials that can not be factored any further, and the computation of polynomial greatest common divisors. The example polynomial above can be factored as (x − 1)(x + 3). A related class of problems is finding algebraic expressions for the roots of a polynomial in a single variable.
Teaching algebra
It has been suggested that elementary algebra should be taught as young as eleven years old,[27] though in recent years it is more common for public lessons to begin at the eighth grade level (≈ 13 y.o. ±) in the United States.[28]Since 1997, Virginia Tech and some other universities have begun using a personalized model of teaching algebra that combines instant feedback from specialized computer software with one-on-one and small group tutoring, which has reduced costs and increased student achievement.[29]Abstract algebra
Abstract algebra extends the familiar concepts found in elementary algebra and arithmetic of numbers to more general concepts. Here are listed fundamental concepts in abstract algebra.Sets: Rather than just considering the different types of numbers, abstract algebra deals with the more general concept of sets: a collection of all objects (called elements) selected by property specific for the set. All collections of the familiar types of numbers are sets. Other examples of sets include the set of all two-by-two matrices, the set of all second-degree polynomials (ax2 + bx + c), the set of all two dimensional vectors in the plane, and the various finite groups such as the cyclic groups, which are the groups of integers modulo n. Set theory is a branch of logic and not technically a branch of algebra.
Binary operations: The notion of addition (+) is abstracted to give a binary operation, ∗ say. The notion of binary operation is meaningless without the set on which the operation is defined. For two elements a and b in a set S, a ∗ b is another element in the set; this condition is called closure. Addition (+), subtraction (-), multiplication (×), and division (÷) can be binary operations when defined on different sets, as are addition and multiplication of matrices, vectors, and polynomials.
Identity elements: The numbers zero and one are abstracted to give the notion of an identity element for an operation. Zero is the identity element for addition and one is the identity element for multiplication. For a general binary operator ∗ the identity element e must satisfy a ∗ e = a and e ∗ a = a. This holds for addition as a + 0 = a and 0 + a = a and multiplication a × 1 = a and 1 × a = a. Not all sets and operator combinations have an identity element; for example, the set of positive natural numbers (1, 2, 3, ...) has no identity element for addition.
Inverse elements: The negative numbers give rise to the concept of inverse elements. For addition, the inverse of a is written −a, and for multiplication the inverse is written a−1. A general two-sided inverse element a−1 satisfies the property that a ∗ a−1 = 1 and a−1 ∗ a = 1 .
Associativity: Addition of integers has a property called associativity. That is, the grouping of the numbers to be added does not affect the sum. For example: (2 + 3) + 4 = 2 + (3 + 4). In general, this becomes (a ∗ b) ∗ c = a ∗ (b ∗ c). This property is shared by most binary operations, but not subtraction or division or octonion multiplication.
Commutativity: Addition and multiplication of real numbers are both commutative. That is, the order of the numbers does not affect the result. For example: 2 + 3 = 3 + 2. In general, this becomes a ∗ b = b ∗ a. This property does not hold for all binary operations. For example, matrix multiplication and quaternion multiplication are both non-commutative.
Groups
Combining the above concepts gives one of the most important structures in mathematics: a group. A group is a combination of a set S and a single binary operation ∗, defined in any way you choose, but with the following properties:- An identity element e exists, such that for every member a of S, e ∗ a and a ∗ e are both identical to a.
- Every element has an inverse: for every member a of S, there exists a member a−1 such that a ∗ a−1 and a−1 ∗ a are both identical to the identity element.
- The operation is associative: if a, b and c are members of S, then (a ∗ b) ∗ c is identical to a ∗ (b ∗ c).
For example, the set of integers under the operation of addition is a group. In this group, the identity element is 0 and the inverse of any element a is its negation, −a. The associativity requirement is met, because for any integers a, b and c, (a + b) + c = a + (b + c)
The nonzero rational numbers form a group under multiplication. Here, the identity element is 1, since 1 × a = a × 1 = a for any rational number a. The inverse of a is 1/a, since a × 1/a = 1.
The integers under the multiplication operation, however, do not form a group. This is because, in general, the multiplicative inverse of an integer is not an integer. For example, 4 is an integer, but its multiplicative inverse is ¼, which is not an integer.
The theory of groups is studied in group theory. A major result in this theory is the classification of finite simple groups, mostly published between about 1955 and 1983, which separates the finite simple groups into roughly 30 basic types.
Semigroups, quasigroups, and monoids are structures similar to groups, but more general. They comprise a set and a closed binary operation, but do not necessarily satisfy the other conditions. A semigroup has an associative binary operation, but might not have an identity element. A monoid is a semigroup which does have an identity but might not have an inverse for every element. A quasigroup satisfies a requirement that any element can be turned into any other by either a unique left-multiplication or right-multiplication; however the binary operation might not be associative.
All groups are monoids, and all monoids are semigroups.
Examples |
||||||||||
| Set: | Natural numbers N | Integers Z | Rational numbers Q (also real R and complex C numbers) | Integers modulo 3: Z3 = {0, 1, 2} | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Operation | + | × (w/o zero) | + | × (w/o zero) | + | − | × (w/o zero) | ÷ (w/o zero) | + | × (w/o zero) |
| Closed | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Identity | 0 | 1 | 0 | 1 | 0 | N/A | 1 | N/A | 0 | 1 |
| Inverse | N/A | N/A | −a | N/A | −a | N/A | 1/a | N/A | 0, 2, 1, respectively | N/A, 1, 2, respectively |
| Associative | Yes | Yes | Yes | Yes | Yes | No | Yes | No | Yes | Yes |
| Commutative | Yes | Yes | Yes | Yes | Yes | No | Yes | No | Yes | Yes |
| Structure | monoid | monoid | abelian group | monoid | abelian group | quasigroup | abelian group | quasigroup | abelian group | abelian group (Z2) |
Rings and fields
Groups just have one binary operation. To fully explain the behaviour of the different types of numbers, structures with two operators need to be studied. The most important of these are rings, and fields.A ring has two binary operations (+) and (×), with × distributive over +. Under the first operator (+) it forms an abelian group. Under the second operator (×) it is associative, but it does not need to have identity, or inverse, so division is not required. The additive (+) identity element is written as 0 and the additive inverse of a is written as −a.
Distributivity generalises the distributive law for numbers. For the integers (a + b) × c = a × c + b × c and c × (a + b) = c × a + c × b, and × is said to be distributive over +.
The integers are an example of a ring. The integers have additional properties which make it an integral domain.
A field is a ring with the additional property that all the elements excluding 0 form an abelian group under ×. The multiplicative (×) identity is written as 1 and the multiplicative inverse of a is written as a−1.
The rational numbers, the real numbers and the complex numbers are all examples of fields.