From Wikipedia, the free encyclopedia
.
Early life
Hendrik Lorentz was born in
Arnhem,
Gelderland,
Netherlands,
the son of Gerrit Frederik Lorentz (1822–1893), a well-off
horticulturist, and Geertruida van Ginkel (1826–1861). In 1862, after
his mother's death, his father married Luberta Hupkes. Despite being
raised as a Protestant, he was a
freethinker in religious matters. From 1866 to 1869, he attended the "Hogere Burger School" in Arnhem, a new type of public high school recently established by
Johan Rudolph Thorbecke.
His results in school were exemplary; not only did he excel in the
physical sciences and mathematics, but also in English, French, and
German. In 1870, he passed the exams in
classical languages which were then required for admission to University.
Lorentz studied
physics and
mathematics at the
Leiden University, where he was strongly influenced by the teaching of astronomy professor
Frederik Kaiser; it was his influence that led him to become a physicist. After earning a
bachelor's degree, he returned to Arnhem in 1871 to teach night school classes in mathematics, but he continued his studies in
Leiden in addition to his teaching position. In 1875, Lorentz earned a
doctoral degree under
Pieter Rijke on a thesis entitled
"Over de theorie der terugkaatsing en breking van het licht" (On the theory of reflection and refraction of light), in which he refined the electromagnetic theory of
James Clerk Maxwell.
Career
Professor in Leiden
During the first twenty years in Leiden, Lorentz was primarily
interested in the electromagnetic theory of electricity, magnetism, and
light. After that, he extended his research to a much wider area while
still focusing on theoretical physics. Lorentz made significant
contributions to fields ranging from
hydrodynamics to
general relativity. His most important contributions were in the area of electromagnetism, the electron theory, and relativity.
Lorentz theorized that
atoms
might consist of charged particles and suggested that the oscillations
of these charged particles were the source of light. When a colleague
and former student of Lorentz's,
Pieter Zeeman, discovered the
Zeeman effect
in 1896, Lorentz supplied its theoretical interpretation. The
experimental and theoretical work was honored with the Nobel prize in
physics in 1902. Lorentz' name is now associated with the
Lorentz-Lorenz formula, the
Lorentz force, the
Lorentzian distribution, and the
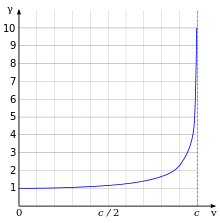
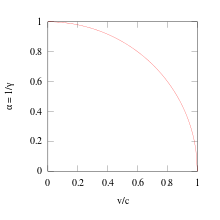
Lorentz transformation.
Electrodynamics and relativity
In 1892 and 1895, Lorentz worked on describing electromagnetic
phenomena (the propagation of light) in reference frames that move
relative to the postulated
luminiferous aether.
He discovered that the transition from one to another reference frame
could be simplified by using a new time variable that he called
local time
and which depended on universal time and the location under
consideration. Although Lorentz did not give a detailed interpretation
of the physical significance of local time, with it, he could explain
the
aberration of light and the result of the
Fizeau experiment. In 1900 and 1904,
Henri Poincaré
called local time Lorentz's "most ingenious idea" and illustrated it by
showing that clocks in moving frames are synchronized by exchanging
light signals that are assumed to travel at the same speed against and
with the motion of the frame. In 1892, with the attempt to explain the
Michelson-Morley experiment, Lorentz also proposed that moving bodies contract in the direction of motion.
In 1899 and again in 1904, Lorentz added
time dilation to his transformations and published what Poincaré in 1905 named
Lorentz transformations.
It was apparently unknown to Lorentz that
Joseph Larmor
had used identical transformations to describe orbiting electrons in
1897. Larmor's and Lorentz's equations look somewhat dissimilar, but
they are algebraically equivalent to those presented by Poincaré and
Einstein in 1905.
Lorentz's 1904 paper includes the covariant formulation of
electrodynamics, in which electrodynamic phenomena in different
reference frames are described by identical equations with well defined
transformation properties. The paper clearly recognizes the
significance of this formulation, namely that the outcomes of
electrodynamic experiments do not depend on the relative motion of the
reference frame. The 1904 paper includes a detailed discussion of the
increase of the inertial mass of rapidly moving objects in a useless
attempt to make momentum look exactly like Newtonian momentum; it was
also an attempt to explain the length contraction as the accumulation of
"stuff" onto mass making it slow and contract.
Lorentz and special relativity
In 1905, Einstein would use many of the concepts, mathematical tools and results Lorentz discussed to write his paper entitled "
On the Electrodynamics of Moving Bodies", known today as the
theory of special relativity. Because Lorentz laid the fundamentals for the work by Einstein, this theory was originally called the
Lorentz-Einstein theory.
In 1906, Lorentz's electron theory received a full-fledged treatment in his lectures at
Columbia University, published under the title The Theory of Electrons.
The increase of mass was the first prediction of Lorentz and Einstein to be tested, but some experiments by
Kaufmann
appeared to show a slightly different mass increase; this led Lorentz
to the famous remark that he was "au bout de mon latin" ("at the end of
my [knowledge of] Latin" = at his wit's end) The confirmation of his prediction had to wait until 1908 and later.
Lorentz published a series of papers dealing with what he called "Einstein's principle of relativity". For instance, in 1909, 1910,
1914.
In his 1906 lectures published with additions in 1909 in the book "The
theory of electrons" (updated in 1915), he spoke affirmatively of
Einstein's theory:
It will be clear by what has been
said that the impressions received by the two observers A0 and A would
be alike in all respects. It would be impossible to decide which of them
moves or stands still with respect to the ether, and there would be no
reason for preferring the times and lengths measured by the one to those
determined by the other, nor for saying that either of them is in
possession of the "true" times or the "true" lengths. This is a point
which Einstein has laid particular stress on, in a theory in which he
starts from what he calls the principle of relativity, [...] I cannot
speak here of the many highly interesting applications which Einstein
has made of this principle. His results concerning electromagnetic and
optical phenomena ... agree in the main with those which we have
obtained in the preceding pages, the chief difference being that
Einstein simply postulates what we have deduced, with some difficulty
and not altogether satisfactorily, from the fundamental equations of the
electromagnetic field. By doing so, he may certainly take credit for
making us see in the negative result of experiments like those of
Michelson, Rayleigh and Brace, not a fortuitous compensation of opposing
effects, but the manifestation of a general and fundamental principle.
[...] It would be unjust not to add that, besides the fascinating
boldness of its starting point, Einstein's theory has another marked
advantage over mine. Whereas I have not been able to obtain for the
equations referred to moving axes exactly the same form as for
those which apply to a stationary system, Einstein has accomplished this
by means of a system of new variables slightly different from those
which I have introduced.
Though Lorentz still maintained that there is an (undetectable) aether in which resting clocks indicate the "true time":
1909: Yet, I think, something may
also be claimed in favour of the form in which I have presented the
theory. I cannot but regard the ether, which can be the seat of an
electromagnetic field with its energy and its vibrations, as endowed
with a certain degree of substantiality, however different it may be
from all ordinary matter.
1910: Provided that there is an aether, then under all systems x, y, z,
t, one is preferred by the fact, that the coordinate axes as well as
the clocks are resting in the aether. If one connects with this the idea
(which I would abandon only reluctantly) that space and time are
completely different things, and that there is a "true time"
(simultaneity thus would be independent of the location, in agreement
with the circumstance that we can have the idea of infinitely great
velocities), then it can be easily seen that this true time should be
indicated by clocks at rest in the aether. However, if the relativity
principle had general validity in nature, one wouldn't be in the
position to determine, whether the reference system just used is the
preferred one. Then one comes to the same results, as if one (following
Einstein and Minkowski) deny the existence of the aether and of true
time, and to see all reference systems as equally valid. Which of these
two ways of thinking one is following, can surely be left to the
individual.
Lorentz also gave credit to Poincaré's contributions to relativity.
Indeed, for some of the physical
quantities which enter the formulas, I did not indicate the
transformation which suits best. That was done by Poincaré and then by
Mr. Einstein and Minkowski [...] I did not succeed in obtaining the
exact invariance of the equations [...] Poincaré, on the contrary,
obtained a perfect invariance of the equations of electrodynamics, and
he formulated the "postulate of relativity", terms which he was the
first to employ. [...] Let us add that by correcting the imperfections
of my work he never reproached me for them.
Lorentz and general relativity
Lorentz was one of few scientists who supported Einstein's search for
general relativity from the beginning – he wrote several research papers and discussed with Einstein personally and by letter. For instance, he attempted to combine Einstein's formalism with
Hamilton's principle (1915),
and to reformulate it in a
coordinate-free way (1916).
Lorentz wrote in 1919:
The total eclipse of the sun of May
29, resulted in a striking confirmation of the new theory of the
universal attractive power of gravitation developed by Albert Einstein,
and thus reinforced the conviction that the defining of this theory is
one of the most important steps ever taken in the domain of natural
science.
Lorentz and quantum mechanics
Assessments
Lorentz-monument Park Sonsbeek. Arnhem. Nederlands
Einstein wrote of Lorentz:
1928: The enormous significance of
his work consisted therein, that it forms the basis for the theory of
atoms and for the general and special theories of relativity. The
special theory was a more detailed expose of those concepts which are
found in Lorentz's research of 1895.
1953: For me personally he meant more than all the others I have met on my life's journey.
Poincaré (1902) said of Lorentz's theory of electrodynamics:
The most satisfactory theory is
that of Lorentz; it is unquestionably the theory that best explains the
known facts, the one that throws into relief the greatest number of
known relations ... it is due to Lorentz that the results of Fizeau
on the optics of moving bodies, the laws of normal and abnormal
dispersion and of absorption are connected with each other ... Look at
the ease with which the new Zeeman phenomenon found its place, and even aided the classification of Faraday's magnetic rotation, which had defied all Maxwell's efforts.
It will be Lorentz's main claim to
fame that he demonstrated that the fundamental equations of
electromagnetism also allow of a group of transformations that enables
them to resume the same form when a transition is made from one
reference system to another. This group differs fundamentally from the above group as regards transformations of space and time.''
Lorentz and
Emil Wiechert
had an interesting correspondence on the topics of electromagnetism and
the theory of relativity, and Lorentz explained his ideas in letters to
Wiechert.
Lorentz was chairman of the first
Solvay Conference
held in Brussels in the autumn of 1911. Shortly after the conference,
Poincaré wrote an essay on quantum physics which gives an indication of
Lorentz's status at the time:
... at every moment [the twenty
physicists from different countries] could be heard talking of the
[quantum mechanics] which they contrasted with the old mechanics. Now
what was the old mechanics? Was it that of Newton, the one which still
reigned uncontested at the close of the nineteenth century? No, it was
the mechanics of Lorentz, the one dealing with the principle of
relativity; the one which, hardly five years ago, seemed to be the
height of boldness.
Change of priorities
In
1910, Lorentz decided to reorganize his life. His teaching and
management duties at Leiden University were taking up too much of his
time, leaving him little time for research. In 1912, he resigned from
his chair of theoretical physics to become curator of the "Physics
Cabinet" at
Teylers Museum in
Haarlem.
He remained connected to Leiden University as an external professor,
and his "Monday morning lectures" on new developments in theoretical
physics soon became legendary.
Lorentz initially asked Einstein to succeed him as professor of
theoretical physics at Leiden. However, Einstein could not accept
because he had just accepted a position at
ETH Zurich.
Einstein had no regrets in this matter, since the prospect of having to
fill Lorentz's shoes made him shiver. Instead Lorentz appointed
Paul Ehrenfest
as his successor in the chair of theoretical physics at the Leiden
University, who would found the Institute for Theoretical Physics which
would become known as the
Lorentz Institute.
Civil work
After
World War I, Lorentz was one of the driving forces behind the founding
of the "Wetenschappelijke Commissie van Advies en Onderzoek in het
Belang van Volkswelvaart en Weerbaarheid", a committee which was to
harness the scientific potential united in the
Royal Netherlands Academy of Arts and Sciences
(KNAW) for solving civil problems such as food shortage which had
resulted from the war. Lorentz was appointed chair of the committee.
However, despite the best efforts of many of the participants the
committee would harvest little success. The only exception being that it
ultimately resulted in the founding of TNO, the
Netherlands Organisation for Applied Scientific Research.
Lorentz was also asked by the Dutch government to chair a committee to calculate some of the effects of the proposed
Afsluitdijk (Enclosure Dam) flood control dam on water levels in the
Waddenzee.
Hydraulic engineering
was mainly an empirical science at that time, but the disturbance of
the tidal flow caused by the Afsluitdijk was so unprecedented that the
empirical rules could not be trusted. Originally Lorentz was only
supposed to have a coordinating role in the committee, but it quickly
became apparent that Lorentz was the only physicist to have any
fundamental traction on the problem. In the period 1918 till 1926,
Lorentz invested a large portion of his time in the problem. Lorentz proposed to start from the basic
hydrodynamic equations of motion and solve the problem numerically. This was feasible for a "
human computer", because of the quasi-one-dimensional nature of the water flow in the
Waddenzee. The Afsluitdijk was completed in 1932, and the predictions of Lorentz and his committee turned out to be remarkably accurate.
One of the two sets of locks in the Afsluitdijk was named after him.
Family life
In
1881, Lorentz married Aletta Catharina Kaiser. Her father was J.W.
Kaiser, a professor at the Academy of Fine Arts. He was the Director of
the museum which later became the well-known
Rijksmuseum (National Gallery). He also was the designer of the first postage stamps of The Netherlands.
There were two daughters, and one son from this marriage.
Dr. Geertruida Luberta Lorentz,
the eldest daughter, was a physicist. She married Professor W.J. de
Haas, who was the Director of the Cryogenic Laboratory at the University
of Leiden.
Death
In January 1928, Lorentz became seriously ill, and died shortly after on February 4. The respect in which he was held in the Netherlands is apparent from
Owen Willans Richardson's description of his funeral:
The funeral took place at Haarlem
at noon on Friday, February 10. At the stroke of twelve the State
telegraph and telephone services of Holland were suspended for three
minutes as a revered tribute to the greatest man the Netherlands has
produced in our time. It was attended by many colleagues and
distinguished physicists from foreign countries. The President, Sir Ernest Rutherford, represented the Royal Society and made an appreciative oration by the graveside.
— O. W. Richardson
Unique 1928 film footage of the funeral procession with a lead
carriage followed by ten mourners, followed by a carriage with the
coffin, followed in turn by at least four more carriages, passing by a
crowd at the
Grote Markt, Haarlem
from the Zijlstraat to the Smedestraat, and then back again through the
Grote Houtstraat towards the Barteljorisstraat, on the way to the
"Algemene Begraafplaats" at the Kleverlaan (northern Haarlem cemetery)
has been digitized on
YouTube. Einstein gave a eulogy at a memorial service at Leiden University.
Legacy
Lorentz is considered one of the prime representatives of the "Second
Dutch Golden Age", a period of several decades surrounding 1900 in which
in the natural sciences in the Netherlands flourished.
Richardson describes Lorentz as:
[A] man of remarkable intellectual powers ... . Although
steeped in his own investigation of the moment, he always seemed to have
in his immediate grasp its ramifications into every corner of the
universe. ... The singular clearness of his writings provides a striking
reflection of his wonderful powers in this respect. .... He possessed
and successfully employed the mental vivacity which is necessary to
follow the interplay of discussion, the insight which is required to
extract those statements which illuminate the real difficulties, and the
wisdom to lead the discussion among fruitful channels, and he did this
so skillfully that the process was hardly perceptible.
M. J. Klein (1967) wrote of Lorentz's reputation in the 1920s:
For many years physicists had always been eager "to hear what
Lorentz will say about it" when a new theory was advanced, and, even at
seventy-two, he did not disappoint them.