A Medley of Potpourri

Tuesday, December 31, 2024

Harmonic

From Wikipedia, the free encyclopedia

In physics, acoustics, and telecommunications, a harmonic is a sinusoidal wave with a frequency that is a positive integer multiple of the fundamental frequency of a periodic signal. The fundamental frequency is also called the 1st harmonic; the other harmonics are known as higher harmonics. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a harmonic series.

The term is employed in various disciplines, including music, physics, acoustics, electronic power transmission, radio technology, and other fields. For example, if the fundamental frequency is 50 Hz, a common AC power supply frequency, the frequencies of the first three higher harmonics are 100 Hz (2nd harmonic), 150 Hz (3rd harmonic), 200 Hz (4th harmonic) and any addition of waves with these frequencies is periodic at 50 Hz.

An $n$ ^th characteristic mode, for $n > 1,$ will have nodes that are not vibrating. For example, the 3^rd characteristic mode will have nodes at $\frac{1}{3} L$ and $\frac{2}{3} L,$ where $L$ is the length of the string. In fact, each $n$ ^th characteristic mode, for $n$ not a multiple of 3, will not have nodes at these points. These other characteristic modes will be vibrating at the positions $\frac{1}{3} L$ and $\frac{2}{3} L .$ If the player gently touches one of these positions, then these other characteristic modes will be suppressed. The tonal harmonics from these other characteristic modes will then also be suppressed. Consequently, the tonal harmonics from the $n$ ^th characteristic characteristic modes, where $n$ is a multiple of 3, will be made relatively more prominent.

In music, harmonics are used on string instruments and wind instruments as a way of producing sound on the instrument, particularly to play higher notes and, with strings, obtain notes that have a unique sound quality or "tone colour". On strings, bowed harmonics have a "glassy", pure tone. On stringed instruments, harmonics are played by touching (but not fully pressing down the string) at an exact point on the string while sounding the string (plucking, bowing, etc.); this allows the harmonic to sound, a pitch which is always higher than the fundamental frequency of the string.

Terminology

Harmonics may be called "overtones", "partials", or "upper partials", and in some music contexts, the terms "harmonic", "overtone" and "partial" are used fairly interchangeably. But more precisely, the term "harmonic" includes all pitches in a harmonic series (including the fundamental frequency) while the term "overtone" only includes pitches above the fundamental.

Characteristics

A whizzing, whistling tonal character, distinguishes all the harmonics both natural and artificial from the firmly stopped intervals; therefore their application in connection with the latter must always be carefully considered.
— Richard Scholz (c. 1888–1912)

Most acoustic instruments emit complex tones containing many individual partials (component simple tones or sinusoidal waves), but the untrained human ear typically does not perceive those partials as separate phenomena. Rather, a musical note is perceived as one sound, the quality or timbre of that sound being a result of the relative strengths of the individual partials. Many acoustic oscillators, such as the human voice or a bowed violin string, produce complex tones that are more or less periodic, and thus are composed of partials that are nearly matched to the integer multiples of fundamental frequency and therefore resemble the ideal harmonics and are called "harmonic partials" or simply "harmonics" for convenience (although it's not strictly accurate to call a partial a harmonic, the first being actual and the second being theoretical).

Oscillators that produce harmonic partials behave somewhat like one-dimensional resonators, and are often long and thin, such as a guitar string or a column of air open at both ends (as with the metallic modern orchestral transverse flute). Wind instruments whose air column is open at only one end, such as trumpets and clarinets, also produce partials resembling harmonics. However they only produce partials matching the odd harmonics—at least in theory. In practical use, no real acoustic instrument behaves as perfectly as the simplified physical models predict; for example, instruments made of non-linearly elastic wood, instead of metal, or strung with gut instead of brass or steel strings, tend to have not-quite-integer partials.

Partials whose frequencies are not integer multiples of the fundamental are referred to as inharmonic partials. Some acoustic instruments emit a mix of harmonic and inharmonic partials but still produce an effect on the ear of having a definite fundamental pitch, such as pianos, strings plucked pizzicato, vibraphones, marimbas, and certain pure-sounding bells or chimes. Antique singing bowls are known for producing multiple harmonic partials or multiphonics. Other oscillators, such as cymbals, drum heads, and most percussion instruments, naturally produce an abundance of inharmonic partials and do not imply any particular pitch, and therefore cannot be used melodically or harmonically in the same way other instruments can.

Building on of Sethares (2004), dynamic tonality introduces the notion of pseudo-harmonic partials, in which the frequency of each partial is aligned to match the pitch of a corresponding note in a pseudo-just tuning, thereby maximizing the consonance of that pseudo-harmonic timbre with notes of that pseudo-just tuning.

Partials, overtones, and harmonics

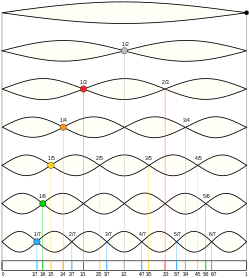
An overtone is any partial higher than the lowest partial in a compound tone. The relative strengths and frequency relationships of the component partials determine the timbre of an instrument. The similarity between the terms overtone and partial sometimes leads to their being loosely used interchangeably in a musical context, but they are counted differently, leading to some possible confusion. In the special case of instrumental timbres whose component partials closely match a harmonic series (such as with most strings and winds) rather than being inharmonic partials (such as with most pitched percussion instruments), it is also convenient to call the component partials "harmonics", but not strictly correct, because harmonics are numbered the same even when missing, while partials and overtones are only counted when present. This chart demonstrates how the three types of names (partial, overtone, and harmonic) are counted (assuming that the harmonics are present):

Frequency	Order ( $n$ )	Name 1	Name 2	Name 3
1 × $f$ = 440 Hz	$n$ = 1	1st partial	fundamental tone	1st harmonic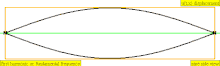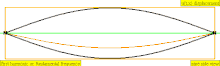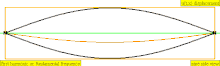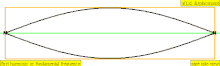
2 × $f$ = 880 Hz	$n$ = 2	2nd partial	1st overtone	2nd harmonic
3 × $f$ = 1320 Hz	$n$ = 3	3rd partial	2nd overtone	3rd harmonic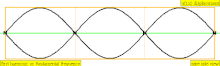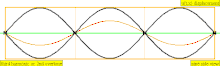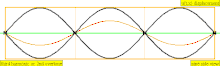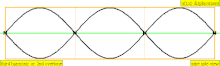
4 × $f$ = 1760 Hz	$n$ = 4	4th partial	3rd overtone	4th harmonic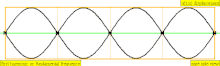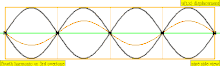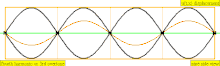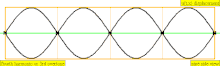

In many musical instruments, it is possible to play the upper harmonics without the fundamental note being present. In a simple case (e.g., recorder) this has the effect of making the note go up in pitch by an octave, but in more complex cases many other pitch variations are obtained. In some cases it also changes the timbre of the note. This is part of the normal method of obtaining higher notes in wind instruments, where it is called overblowing. The extended technique of playing multiphonics also produces harmonics. On string instruments it is possible to produce very pure sounding notes, called harmonics or flageolets by string players, which have an eerie quality, as well as being high in pitch. Harmonics may be used to check at a unison the tuning of strings that are not tuned to the unison. For example, lightly fingering the node found halfway down the highest string of a cello produces the same pitch as lightly fingering the node ⁠ 1 / 3 ⁠ of the way down the second highest string. For the human voice see Overtone singing, which uses harmonics.

While it is true that electronically produced periodic tones (e.g. square waves or other non-sinusoidal waves) have "harmonics" that are whole number multiples of the fundamental frequency, practical instruments do not all have this characteristic. For example, higher "harmonics" of piano notes are not true harmonics but are "overtones" and can be very sharp, i.e. a higher frequency than given by a pure harmonic series. This is especially true of instruments other than strings, brass, or woodwinds. Examples of these "other" instruments are xylophones, drums, bells, chimes, etc.; not all of their overtone frequencies make a simple whole number ratio with the fundamental frequency. (The fundamental frequency is the reciprocal of the longest time period of the collection of vibrations in some single periodic phenomenon.)

On stringed instruments

Harmonics may be singly produced [on stringed instruments] (1) by varying the point of contact with the bow, or (2) by slightly pressing the string at the nodes, or divisions of its aliquot parts ( $\frac{1}{2}$ , $\frac{1}{3}$ , $\frac{1}{4}$ , etc.). (1) In the first case, advancing the bow from the usual place where the fundamental note is produced, towards the bridge, the whole scale of harmonics may be produced in succession, on an old and highly resonant instrument. The employment of this means produces the effect called 'sul ponticello.' (2) The production of harmonics by the slight pressure of the finger on the open string is more useful. When produced by pressing slightly on the various nodes of the open strings they are called 'natural harmonics'. ... Violinists are well aware that the longer the string in proportion to its thickness, the greater the number of upper harmonics it can be made to yield.
— Grove's Dictionary of Music and Musicians (1879)

The following table displays the stop points on a stringed instrument at which gentle touching of a string will force it into a harmonic mode when vibrated. String harmonics (flageolet tones) are described as having a "flutelike, silvery quality" that can be highly effective as a special color or tone color (timbre) when used and heard in orchestration. It is unusual to encounter natural harmonics higher than the fifth partial on any stringed instrument except the double bass, on account of its much longer strings.

Harmonic order	Stop note	Note sounded (relative to open string)	Audio frequency (Hz)	Cents above fundamental (offset by octave)	Audio (octave shifted)
1^st	fundamental, perfect unison	P 1	600Hz	0.0 $¢$	Play^ⓘ
2^nd	first perfect octave	P 8	1200Hz	0.0 $¢$	Play^ⓘ
3^rd	perfect fifth	P 8 + P 5	1800Hz	702.0 $¢$	Play^ⓘ
4^th	doubled perfect octave	2 · P 8	2400Hz	0.0 $¢$	Play^ⓘ
5^th	just major third, major third	2 · P 8 + ^M3	3000Hz	386.3 $¢$	Play^ⓘ
6^th	perfect fifth	2 · P 8 + P 5	3600Hz	702.0 $¢$	Play^ⓘ
7^th	harmonic seventh, septimal minor seventh (‘the lost chord’)	2 · P 8 + m 7^↓	4200Hz	968.8 $¢$	Play^ⓘ
8^th	third perfect octave	3 · P 8	4800Hz	0.0 $¢$	Play^ⓘ
9^th	Pythagorean major second harmonic ninth	3 · P 8 + ^M2	5400Hz	203.9 $¢$	Play^ⓘ
10^th	just major third	3 · P 8 + ^M3	6000Hz	386.3 $¢$	Play^ⓘ
11^th	lesser undecimal tritone, undecimal semi-augmented fourth	3 · P 8 + ^A4	6600Hz	551.3 $¢$	Play^ⓘ
12^th	perfect fifth	3 · P 8 + P 5	7200Hz	702.0 $¢$	Play^ⓘ
13^th	tridecimal neutral sixth	3 · P 8 + n 6^↓	7800Hz	840.5 $¢$	Play^ⓘ
14^th	harmonic seventh, septimal minor seventh (‘the lost chord’)	3 · P 8 + m 7^⤈	8400Hz	968.8 $¢$	Play^ⓘ
15^th	just major seventh	3 · P 8 + ^M7	9000Hz	1088.3 $¢$	Play^ⓘ
16^th	fourth perfect octave	4 · P 8	9600Hz	0.0 $¢$	Play^ⓘ
17^th	septidecimal semitone	4 · P 8 + m 2^⇟	10200Hz	105.0 $¢$	Play^ⓘ
18^th	Pythagorean major second	4 · P 8 + ^M2	10800Hz	203.9 $¢$	Play^ⓘ
19^th	nanodecimal minor third	4 · P 8 + m 3	11400Hz	297.5 $¢$	Play^ⓘ
20^th	just major third	4 · P 8 + ^M3	12000Hz	386.3 $¢$	Play^ⓘ

**Notation key**
P	perfect interval
^A	augmented interval (sharpened)
^M	major interval
m	minor interval (flattened major)
n	neutral interval (between major and minor)
	half-flattened (approximate) ( $\approx -38 ¢$ for just, $-50 ¢$ for 12 TET)
^↓	flattened by a syntonic comma (approximate) ( $\approx -21 ¢$ )
^⤈	flattened by a half-comma (approximate) ( $\approx -10 ¢$ )
^⇟	flattened by a quarter-comma (approximate) ( $\approx -5 ¢$ )

Artificial harmonics

Occasionally a score will call for an artificial harmonic, produced by playing an overtone on an already stopped string. As a performance technique, it is accomplished by using two fingers on the fingerboard, the first to shorten the string to the desired fundamental, with the second touching the node corresponding to the appropriate harmonic.

Other information

Harmonics may be either used in or considered as the basis of just intonation systems. Composer Arnold Dreyblatt is able to bring out different harmonics on the single string of his modified double bass by slightly altering his unique bowing technique halfway between hitting and bowing the strings. Composer Lawrence Ball uses harmonics to generate music electronically.

Change detection

From Wikipedia, the free encyclopedia

In statistical analysis, change detection or change point detection tries to identify times when the probability distribution of a stochastic process or time series changes. In general the problem concerns both detecting whether or not a change has occurred, or whether several changes might have occurred, and identifying the times of any such changes.

Specific applications, like step detection and edge detection, may be concerned with changes in the mean, variance, correlation, or spectral density of the process. More generally change detection also includes the detection of anomalous behavior: anomaly detection.

In offline change point detection it is assumed that a sequence of length $T$ is available and the goal is to identify whether any change point(s) occurred in the series. This is an example of post hoc analysis and is often approached using hypothesis testing methods. By contrast, online change point detection is concerned with detecting change points in an incoming data stream.

Background

A time series measures the progression of one or more quantities over time. For instance, the figure above shows the level of water in the Nile river between 1870 and 1970. Change point detection is concerned with identifying whether, and if so when, the behavior of the series changes significantly. In the Nile river example, the volume of water changes significantly after a dam was built in the river. Importantly, anomalous observations that differ from the ongoing behavior of the time series are not generally considered change points as long as the series returns to its previous behavior afterwards.

Mathematically, we can describe a time series as an ordered sequence of observations $(x_{1}, x_{2}, \dots)$ . We can write the joint distribution of a subset $x_{a : b} = (x_{a}, x_{a + 1}, \dots, x_{b})$ of the time series as $p (x_{a : b})$ . If the goal is to determine whether a change point occurred at a time $τ$ in a finite time series of length $T$ , then we really ask whether $p (x_{1 : τ})$ equals $p (x_{τ + 1 : T})$ . This problem can be generalized to the case of more than one change point.

Algorithms

Online change detection

Using the sequential analysis ("online") approach, any change test must make a trade-off between these common metrics:

In a Bayes change-detection problem, a prior distribution is available for the change time.

Online change detection is also done using streaming algorithms.

Offline change detection

Basseville (1993, Section 2.6) discusses offline change-in-mean detection with hypothesis testing based on the works of Page and Picard and maximum-likelihood estimation of the change time, related to two-phase regression. Other approaches employ clustering based on maximum likelihood estimation,, use optimization to infer the number and times of changes, via spectral analysis, or singular spectrum analysis.

Statistically speaking, change detection is often considered as a model selection problem.Models with more changepoints fit data better but with more parameters. The best trade-off can be found by optimizing a model selection criterion such as Akaike information criterion and Bayesian information criterion. Bayesian model selection has also been used. Bayesian methods often quantify uncertainties of all sorts and answer questions hard to tackle by classical methods, such as what is the probability of having a change at a given time and what is the probability of the data having a certain number of changepoints.

"Offline" approaches cannot be used on streaming data because they need to compare to statistics of the complete time series, and cannot react to changes in real-time but often provide a more accurate estimation of the change time and magnitude.

Applications

Change detection tests are often used in manufacturing for quality control, intrusion detection, spam filtering, website tracking, and medical diagnostics.

Linguistic change detection

Linguistic change detection refers to the ability to detect word-level changes across multiple presentations of the same sentence. Researchers have found that the amount of semantic overlap (i.e., relatedness) between the changed word and the new word influences the ease with which such a detection is made (Sturt, Sanford, Stewart, & Dawydiak, 2004). Additional research has found that focussing one's attention to the word that will be changed during the initial reading of the original sentence can improve detection. This was shown using italicized text to focus attention, whereby the word that will be changing is italicized in the original sentence (Sanford, Sanford, Molle, & Emmott, 2006), as well as using clefting constructions such as "It was the tree that needed water." (Kennette, Wurm, & Van Havermaet, 2010). These change-detection phenomena appear to be robust, even occurring cross-linguistically when bilinguals read the original sentence in their native language and the changed sentence in their second language (Kennette, Wurm & Van Havermaet, 2010). Recently, researchers have detected word-level changes in semantics across time by computationally analyzing temporal corpora (for example: the word "gay" has acquired a new meaning over time) using change point detection. This is also applicable to reading non-words such as music. Even though music is not a language, it is still written and people to comprehend its meaning which involves perception and attention, allowing change detection to be present.

Visual change detection

Visual change detection is one's ability to detect differences between two or more images or scenes. This is essential in many everyday tasks. One example is detecting changes on the road to drive safely and successfully. Change detection is crucial in operating motor vehicles to detect other vehicles, traffic control signals, pedestrians, and more. Another example of utilizing visual change detection is facial recognition. When noticing one's appearance, change detection is vital, as faces are "dynamic" and can change in appearance due to different factors such as "lighting conditions, facial expressions, aging, and occlusion". Change detection algorithms use various techniques, such as "feature tracking, alignment, and normalization," to capture and compare different facial features and patterns across individuals in order to correctly identify people. Visual change detection involves the integration of "multiple sensors inputs, cognitive processes, and attentional mechanisms," often focusing on multiple stimuli at once. The brain processes visual information from the eyes, compares it with previous knowledge stored in memory, and identifies differences between the two stimuli. This process occurs rapidly and unconsciously, allowing individuals to respond to changing environments and make necessary adjustments to their behavior.

Cognitive change detection

There have been several studies conducted to analyze the cognitive functions of change detection. With cognitive change detection, researchers have found that most people overestimate their change detection, when in reality, they are more susceptible to change blindness than they think. Cognitive change detection has many complexities based on external factors, and sensory pathways play a key role in determining one's success in detecting changes. One study proposes and proves that the multi-sensory pathway network, which consists of three sensory pathways, significantly increases the effectiveness of change detection. Sensory pathway one fuses the stimuli together, sensory pathway two involves using the middle concatenation strategy to learn the changed behavior, and sensory pathway three involves using the middle difference strategy to learn the changed behavior. With all three of these working together, change detection has a significantly increased success rate. It was previously believed that the posterior parietal cortex (PPC) played a role in enhancing change detection due to its focus on "sensory and task-related activity". However, studies have also disproven that the PPC is necessary for change detection; although these have high functional correlation with each other, the PPC's mechanistic involvement in change detection is insignificant. Moreover, top-down processing plays an important role in change detection because it enables people to resort to background knowledge which then influences perception, which is also common in children. Researchers have conducted a longitudinal study surrounding children's development and the change detection throughout infancy to adulthood. In this, it was found that change detection is stronger in young infants compared to older children, with top-down processing being a main contributor to this outcome.