Fault tree analysis

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Fault_tree_analysis 

 

A fault tree diagram

Fault tree analysis (FTA) is a type of failure analysis in which an undesired state of a system is examined. This analysis method is mainly used in safety engineering and reliability engineering to understand how systems can fail, to identify the best ways to reduce risk and to determine (or get a feeling for) event rates of a safety accident or a particular system level (functional) failure. FTA is used in the aerospace, nuclear power, chemical and process, pharmaceutical, petrochemical and other high-hazard industries; but is also used in fields as diverse as risk factor identification relating to social service system failure. FTA is also used in software engineering for debugging purposes and is closely related to cause-elimination technique used to detect bugs.

In aerospace, the more general term "system failure condition" is used for the "undesired state" / top event of the fault tree. These conditions are classified by the severity of their effects. The most severe conditions require the most extensive fault tree analysis. These system failure conditions and their classification are often previously determined in the functional hazard analysis.

Usage

Fault tree analysis can be used to:

• understand the logic leading to the top event / undesired state.
• show compliance with the (input) system safety / reliability requirements.
• prioritize the contributors leading to the top event- creating the critical equipment/parts/events lists for different importance measures
• monitor and control the safety performance of the complex system (e.g., is a particular aircraft safe to fly when fuel valve x malfunctions? For how long is it allowed to fly with the valve malfunction?).
• minimize and optimize resources.
• assist in designing a system. The FTA can be used as a design tool that helps to create (output / lower level) requirements.
• function as a diagnostic tool to identify and correct causes of the top event. It can help with the creation of diagnostic manuals / processes.

History

Fault tree analysis (FTA) was originally developed in 1962 at Bell Laboratories by H.A. Watson, under a U.S. Air Force Ballistics Systems Division contract to evaluate the Minuteman I Intercontinental Ballistic Missile (ICBM) Launch Control System. The use of fault trees has since gained widespread support and is often used as a failure analysis tool by reliability experts. Following the first published use of FTA in the 1962 Minuteman I Launch Control Safety Study, Boeing and AVCO expanded use of FTA to the entire Minuteman II system in 1963–1964. FTA received extensive coverage at a 1965 System Safety Symposium in Seattle sponsored by Boeing and the University of Washington. Boeing began using FTA for civil aircraft design around 1966.

Subsequently, within the U.S. military, application of FTA for use with fuses was explored by Picatinny Arsenal in the 1960s and 1970s. In 1976 the U.S. Army Materiel Command incorporated FTA into an Engineering Design Handbook on Design for Reliability. The Reliability Analysis Center at Rome Laboratory and its successor organizations now with the Defense Technical Information Center (Reliability Information Analysis Center, and now Defense Systems Information Analysis Center) has published documents on FTA and reliability block diagrams since the 1960s. MIL-HDBK-338B provides a more recent reference.

In 1970, the U.S. Federal Aviation Administration (FAA) published a change to 14 CFR 25.1309 airworthiness regulations for transport category aircraft in the Federal Register at 35 FR 5665 (1970-04-08). This change adopted failure probability criteria for aircraft systems and equipment and led to widespread use of FTA in civil aviation. In 1998, the FAA published Order 8040.4, establishing risk management policy including hazard analysis in a range of critical activities beyond aircraft certification, including air traffic control and modernization of the U.S. National Airspace System. This led to the publication of the FAA System Safety Handbook, which describes the use of FTA in various types of formal hazard analysis.

Early in the Apollo program the question was asked about the probability of successfully sending astronauts to the moon and returning them safely to Earth. A risk, or reliability, calculation of some sort was performed and the result was a mission success probability that was unacceptably low. This result discouraged NASA from further quantitative risk or reliability analysis until after the Challenger accident in 1986. Instead, NASA decided to rely on the use of failure modes and effects analysis (FMEA) and other qualitative methods for system safety assessments. After the Challenger accident, the importance of probabilistic risk assessment (PRA) and FTA in systems risk and reliability analysis was realized and its use at NASA has begun to grow and now FTA is considered as one of the most important system reliability and safety analysis techniques.

Within the nuclear power industry, the U.S. Nuclear Regulatory Commission began using PRA methods including FTA in 1975, and significantly expanded PRA research following the 1979 incident at Three Mile Island. This eventually led to the 1981 publication of the NRC Fault Tree Handbook NUREG–0492, and mandatory use of PRA under the NRC's regulatory authority.

Following process industry disasters such as the 1984 Bhopal disaster and 1988 Piper Alpha explosion, in 1992 the United States Department of Labor Occupational Safety and Health Administration (OSHA) published in the Federal Register at 57 FR 6356 (1992-02-24) its Process Safety Management (PSM) standard in 19 CFR 1910.119. OSHA PSM recognizes FTA as an acceptable method for process hazard analysis (PHA).

Today FTA is widely used in system safety and reliability engineering, and in all major fields of engineering.

Methodology

FTA methodology is described in several industry and government standards, including NRC NUREG–0492 for the nuclear power industry, an aerospace-oriented revision to NUREG–0492 for use by NASA, SAE ARP4761 for civil aerospace, MIL–HDBK–338 for military systems, IEC standard IEC 61025 is intended for cross-industry use and has been adopted as European Norm EN 61025.

Any sufficiently complex system is subject to failure as a result of one or more subsystems failing. The likelihood of failure, however, can often be reduced through improved system design. Fault tree analysis maps the relationship between faults, subsystems, and redundant safety design elements by creating a logic diagram of the overall system.

The undesired outcome is taken as the root ('top event') of a tree of logic. For instance the undesired outcome of a metal stamping press operation is a human appendage being stamped. Working backward from this top event we might determine there are two ways this could happen: during normal operation or during maintenance operation. This condition is a logical OR. Considering the branch of occurring during normal operation perhaps we determine there are two ways this could happen: the press cycles and harms the operator or the press cycles and harms another person. This is another logical OR. We can make a design improvement by requiring the operator to press two buttons to cycle the machine—this is a safety feature in the form of a logical AND. The button may have an intrinsic failure rate—this becomes a fault stimulus we can analyze. When fault trees are labeled with actual numbers for failure probabilities, computer programs can calculate failure probabilities from fault trees. When a specific event is found to have more than one effect event, i.e. it has impact on several subsystems, it is called a common cause or common mode. Graphically speaking, it means this event will appear at several locations in the tree. Common causes introduce dependency relations between events. The probability computations of a tree which contains some common causes are much more complicated than regular trees where all events are considered as independent. Not all software tools available on the market provide such capability.

The tree is usually written out using conventional logic gate symbols. A cut set is a combination of events, typically component failures, causing the top event. If no event can be removed from a cut set without failing to cause the top event, then it is called a minimal cut set.

Some industries use both fault trees and event trees (see Probabilistic Risk Assessment). An event tree starts from an undesired initiator (loss of critical supply, component failure etc.) and follows possible further system events through to a series of final consequences. As each new event is considered, a new node on the tree is added with a split of probabilities of taking either branch. The probabilities of a range of 'top events' arising from the initial event can then be seen.

Classic programs include the Electric Power Research Institute's (EPRI) CAFTA software, which is used by many of the US nuclear power plants and by a majority of US and international aerospace manufacturers, and the Idaho National Laboratory's SAPHIRE, which is used by the U.S. Government to evaluate the safety and reliability of nuclear reactors, the Space Shuttle, and the International Space Station. Outside the US, the software RiskSpectrum is a popular tool for fault tree and event tree analysis, and is licensed for use at almost half of the world's nuclear power plants for probabilistic safety assessment. Professional-grade free software is also widely available; SCRAM is an open-source tool that implements the Open-PSA Model Exchange Format open standard for probabilistic safety assessment applications.

Graphic symbols

The basic symbols used in FTA are grouped as events, gates, and transfer symbols. Minor variations may be used in FTA software.

Event symbols

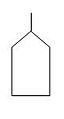
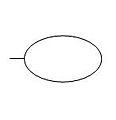
Event symbols are used for primary events and intermediate events. Primary events are not further developed on the fault tree. Intermediate events are found at the output of a gate. The event symbols are shown below:

• 

  Basic event

• 

  External event

• 

  Undeveloped event

• 

  Conditioning event

• 

  Intermediate event

The primary event symbols are typically used as follows:

• Basic event - failure or error in a system component or element (example: switch stuck in open position)
• External event - normally expected to occur (not of itself a fault)
• Undeveloped event - an event about which insufficient information is available, or which is of no consequence
• Conditioning event - conditions that restrict or affect logic gates (example: mode of operation in effect)

An intermediate event gate can be used immediately above a primary event to provide more room to type the event description.

FTA is a top-to-bottom approach.

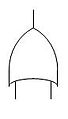
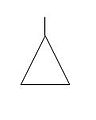
Gate symbols

Gate symbols describe the relationship between input and output events. The symbols are derived from Boolean logic symbols:

• 

  OR gate

• 

  AND gate

• 

  Exclusive OR gate

• 

  Priority AND gate

• 

  Inhibit gate

The gates work as follows:

• OR gate - the output occurs if any input occurs.
• AND gate - the output occurs only if all inputs occur (inputs are independent from the source).
• Exclusive OR gate - the output occurs if exactly one input occurs.
• Priority AND gate - the output occurs if the inputs occur in a specific sequence specified by a conditioning event.
• Inhibit gate - the output occurs if the input occurs under an enabling condition specified by a conditioning event.

Transfer symbols

Transfer symbols are used to connect the inputs and outputs of related fault trees, such as the fault tree of a subsystem to its system. NASA prepared a complete document about FTA through practical incidents.

• 

  Transfer in

• 

  Transfer out

Basic mathematical foundation

Events in a fault tree are associated with statistical probabilities or Poisson-Exponentially distributed constant rates. For example, component failures may typically occur at some constant failure rate λ (a constant hazard function). In this simplest case, failure probability depends on the rate λ and the exposure time t:

${\displaystyle P=1-e^{-\lambda t}}$

where:

${\displaystyle P\approx \lambda t}$ if ${\displaystyle \lambda t<0.001}$

A fault tree is often normalized to a given time interval, such as a flight hour or an average mission time. Event probabilities depend on the relationship of the event hazard function to this interval.

Unlike conventional logic gate diagrams in which inputs and outputs hold the binary values of TRUE (1) or FALSE (0), the gates in a fault tree output probabilities related to the set operations of Boolean logic. The probability of a gate's output event depends on the input event probabilities.

An AND gate represents a combination of independent events. That is, the probability of any input event to an AND gate is unaffected by any other input event to the same gate. In set theoretic terms, this is equivalent to the intersection of the input event sets, and the probability of the AND gate output is given by:

P (A and B) = P (A ∩ B) = P(A) P(B)

An OR gate, on the other hand, corresponds to set union:

P (A or B) = P (A ∪ B) = P(A) + P(B) - P (A ∩ B)

Since failure probabilities on fault trees tend to be small (less than .01), P (A ∩ B) usually becomes a very small error term, and the output of an OR gate may be conservatively approximated by using an assumption that the inputs are mutually exclusive events:

P (A or B) ≈ P(A) + P(B), P (A ∩ B) ≈ 0

An exclusive OR gate with two inputs represents the probability that one or the other input, but not both, occurs:

P (A xor B) = P(A) + P(B) - 2P (A ∩ B)

Again, since P (A ∩ B) usually becomes a very small error term, the exclusive OR gate has limited value in a fault tree.

Quite often, Poisson-Exponentially distributed rates are used to quantify a fault tree instead of probabilities. Rates are often modeled as constant in time while probability is a function of time. Poisson-Exponential events are modelled as infinitely short so no two events can overlap. An OR gate is the superposition (addition of rates) of the two input failure frequencies or failure rates which are modeled as Poisson point processes. The output of an AND gate is calculated using the unavailability (Q₁) of one event thinning the Poisson point process of the other event (λ₂). The unavailability (Q₂) of the other event then thins the Poisson point process of the first event (λ₁). The two resulting Poisson point processes are superimposed according to the following equations.

The output of an AND gate is the combination of independent input events 1 and 2 to the AND gate:

Failure Frequency = λ₁Q₂ + λ₂Q₁ where Q = 1 - e^λt ≈ λt if λt < 0.001

Failure Frequency ≈ λ₁λ₂t₂ + λ₂λ₁t₁ if λ₁t₁ < 0.001 and λ₂t₂ < 0.001

In a fault tree, unavailability (Q) may be defined as the unavailability of safe operation and may not refer to the unavailability of the system operation depending on how the fault tree was structured. The input terms to the fault tree must be carefully defined.

Analysis

Many different approaches can be used to model a FTA, but the most common and popular way can be summarized in a few steps. A single fault tree is used to analyze one and only one undesired event, which may be subsequently fed into another fault tree as a basic event. Though the nature of the undesired event may vary dramatically, a FTA follows the same procedure for any undesired event; be it a delay of 0.25 ms for the generation of electrical power, an undetected cargo bay fire, or the random, unintended launch of an ICBM.

FTA analysis involves five steps:

1. Define the undesired event to study.
   • Definition of the undesired event can be very hard to uncover, although some of the events are very easy and obvious to observe. An engineer with a wide knowledge of the design of the system is the best person to help define and number the undesired events. Undesired events are used then to make FTAs. Each FTA is limited to one undesired event.
2. Obtain an understanding of the system.
   • Once the undesired event is selected, all causes with probabilities of affecting the undesired event of 0 or more are studied and analyzed. Getting exact numbers for the probabilities leading to the event is usually impossible for the reason that it may be very costly and time-consuming to do so. Computer software is used to study probabilities; this may lead to less costly system analysis.
     System analysts can help with understanding the overall system. System designers have full knowledge of the system and this knowledge is very important for not missing any cause affecting the undesired event. For the selected event all causes are then numbered and sequenced in the order of occurrence and then are used for the next step which is drawing or constructing the fault tree.
3. Construct the fault tree.
   • After selecting the undesired event and having analyzed the system so that we know all the causing effects (and if possible their probabilities) we can now construct the fault tree. Fault tree is based on AND and OR gates which define the major characteristics of the fault tree.
4. Evaluate the fault tree.
   • After the fault tree has been assembled for a specific undesired event, it is evaluated and analyzed for any possible improvement or in other words study the risk management and find ways for system improvement. A wide range of qualitative and quantitative analysis methods can be applied. This step is as an introduction for the final step which will be to control the hazards identified. In short, in this step we identify all possible hazards affecting the system in a direct or indirect way.
5. Control the hazards identified.
   • This step is very specific and differs largely from one system to another, but the main point will always be that after identifying the hazards all possible methods are pursued to decrease the probability of occurrence.

Comparison with other analytical methods

FTA is a deductive, top-down method aimed at analyzing the effects of initiating faults and events on a complex system. This contrasts with failure mode and effects analysis (FMEA), which is an inductive, bottom-up analysis method aimed at analyzing the effects of single component or function failures on equipment or subsystems. FTA is very good at showing how resistant a system is to single or multiple initiating faults. It is not good at finding all possible initiating faults. FMEA is good at exhaustively cataloging initiating faults, and identifying their local effects. It is not good at examining multiple failures or their effects at a system level. FTA considers external events, FMEA does not. In civil aerospace the usual practice is to perform both FTA and FMEA, with a failure mode effects summary (FMES) as the interface between FMEA and FTA.

Alternatives to FTA include dependence diagram (DD), also known as reliability block diagram (RBD) and Markov analysis. A dependence diagram is equivalent to a success tree analysis (STA), the logical inverse of an FTA, and depicts the system using paths instead of gates. DD and STA produce probability of success (i.e., avoiding a top event) rather than probability of a top event.

Insects in medicine

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Insects_in_medicine 

 

Maggot debridement therapy on a wound on a diabetic foot

Insects have long been used in medicine, both traditional and modern, sometimes with little evidence of their effectiveness. For the purpose of the article, and in line with custom, medicinal uses of other arthropods such as spiders are included.

Traditional and alternative uses

The medicinal uses of insects and other arthropods worldwide have been reviewed by Meyer-Rochow, who provides examples of all major insect groups, spiders, worms and molluscs and discusses their potential as suppliers of bioactive components. Using insects (and spiders) to treat various maladies and injuries has a long tradition and, having stood the test of time, can be effective and provide results. However, sometimes folk-medicinal "logic" was based on the Doctrine of Signatures = "let likes be cured by likes"and had, if any at all, little more than a psychological effect. For example, to treat cases of constipation, dung beetles were prescribed; to slim down stick insects were thought to help; hairy tarantulas seemed the right treatment for hair loss and fat grubs resembling the swollen limb caused by the parasite Wuchereria bancrofti were expected to help the elephantiasis sufferer. An organism bearing parts that resemble human body parts, animals, or other objects, was thought to have useful relevance to those parts, animals or objects. So, for example, the femurs of grasshoppers, which were said to resemble the human liver, were used to treat liver ailments by the indigenous peoples of Mexico. This doctrine is common throughout traditional and alternative medicine, but is most prominent where medical traditions are broadly accepted, as in traditional Chinese medicine and Ayurveda, and less by community and family based medicine, as is more common in parts of Africa.

Traditional Chinese medicine

Traditional Chinese medicine includes the use of herbal medicine, acupuncture, massage, exercise, and dietary therapy. It is a typical component of modern medical care throughout East Asia and in some parts of Southeast Asia (such as Thailand). Insects are very commonly incorporated as part of the herbal medicine component of traditional Chinese medicine, and their medical properties and applications are broadly accepted and agreed upon. Some brief examples follow:

The Chinese Black Mountain Ant, Polyrhachis vicina, is supposed to act as a cure all and is widely used, especially by the elderly. It is said to prolong life, to have anti-aging properties, to replenish Qi, and to increase virility and fertility. Recent interest in the ants' medicinal qualities has led to British researchers to study the extract's potential to serve as a cancer-fighting agent. Chinese Black Mountain Ant extract is typically consumed mixed with wine.

India and Ayurveda

Ayurveda is ancient traditional Indian treatment almost universally incorporated alongside Western medicine as a typical component of medical treatment in India. Although Ayurvedic medicine is often effective, doses can be inconsistent, and may sometimes be contaminated with toxic heavy metals. Some brief examples to follow:

Termite is said to cure a variety of diseases, both specific and vague. Typically the mound or a portion of the mound is dug up and the termites and the architectural components of the mound are together ground into a paste which is then applied topically to the affected areas or, more rarely, mixed with water and consumed. This treatment was said to cure ulcers, rheumatic diseases, and anemia. It was also suggested to be a general pain reliever and health improver.

The Jatropha Leaf Miner, a lepidopteran which feeds preferentially on Jatropha, is an example of a major insect agricultural pest which is also a medicinal remedy. The larvae, which are also the form of the insect with the greatest economic impact on agriculture, are harvested, boiled, and mashed into a paste which is administered topically and is said to induce lactation, reduce fever, and soothe gastrointestinal tracts.

Africa

Unlike China and India, the traditional insect medicine of Africa is extremely variable. It is largely regional, with few, if any, major agreements on which insects are useful as treatments for which ailments. Most insect medicinal treatments are passed on through communities and families, rather than being taught in university settings, as Traditional Chinese Medicine and Ayurveda sometimes are; furthermore, most traditional medicine practices necessitate a person in a "healer" role. Some brief examples to follow:

Grasshopper is both commonly eaten as a delicacy and an excellent source of protein and is consumed for medicinal purposes. These insects are typically collected, dried in the sun, and then ground into a powder. The powder can then be turned into a paste when mixed with water and ash and applied to the forehead to alleviate the pain of violent headaches. Additionally, the headaches themselves can be prevented by a "healer" inserting the paste under the skin at the nape of the afflicted person's neck.

Termites are also used in parts of Africa much like they are in India. Parts of the mound are dug up, boiled, and turned into a paste, which can then be applied to external wounds to prevent infection or consumed to treat internal hemorrhages. termites are used not only as a form of medicine, but also as a medical device. If a "healer" wants to insert a medicine subcutaneously, they will often spread that medicine on the skin of the patient, and then agitate a termite and place the insect on the skin of the patient. When the termite bites, its mandibles effectively serve as an injection device.

Americas

The Americas were more highly influenced by the Doctrine of Signatures than China, India, or Africa, most likely because of their colonial history with Europe. The majority of insect use in medicine is associated with Central America and parts of South America, rather than North America, and most of it is based on the medical techniques of indigenous peoples. Currently, insect medicine is practiced much more rarely than in China, India, or Africa, though it is still relatively common in rural areas with large indigenous populations. Some examples to follow:

Chapulines, or grasshoppers, are commonly consumed as a toasted regional dish in some parts of Mexico, but they are also used medicinally. They are said to serve as diuretic to treat kidney diseases, to reduce swelling, and to relieve the pain of intestinal disorders when they are consumed. However, there are some risks associated with consuming chapulines, as they are known to harbor nematodes which may be transmitted to humans upon consumption.

Much like the termites of Africa, ants were sometimes used as medicinal devices by the indigenous peoples of Central America. The soldier cast of the Army ant would be collected and used as living sutures by Mayans. This involved agitating an ant and holding its mandibles up to the wound edges; when it bit down, the thorax and abdomen were removed, leaving the head holding the wound together. The ant's salivary gland secretions were reputed to have antibiotic properties. The venom of the Red harvester ant was used to treat rheumatism, arthritis, and poliomyelitis via the immunological reaction produced by its sting. This technique, in which ants are allowed to sting afflicted areas in a controlled manner, is still used in some arid rural areas of Mexico.

The silkworm, Bombyx mori, was also commonly consumed both as a regional food and for medicinal purposes in Central America after it was brought to the New World by the Spanish and Portuguese. Only the immatures are consumed. Boiled pupae were eaten to treat apoplexy, aphasy, bronchitis, pneumonia, convulsions, hemorrhages, and frequent urination. The excrement produced by the larvae is also eaten to improve circulation and alleviate the symptoms of cholera (intense vomiting and diarrhea).

Honey bee products

Honey bee products are used medicinally across Asia, Europe, Africa, Australia, and the Americas, despite the fact that the honey bee was not introduced to the Americas until the colonization by Spain and Portugal. They are by far the most common medical insect product, both historically and currently.

Honey is the most frequently referenced medical bee material. It can be applied to skin to treat excessive scar tissue, rashes, and burns, and can be applied as a poultice to eyes to treat infection. It is also consumed for digestive problems and as a general health restorative, and can be heated and consumed to treat head colds, cough, throat infections, laryngitis, tuberculosis, and lung diseases.

Additionally, apitoxin, or honey bee venom, can be applied via direct stings to relieve arthritis, rheumatism, polyneuritis, and asthma. Propolis, a resinous, waxy mixture collected by honeybees and used as a hive insulator and sealant, is often consumed by menopausal women because of its high hormone content, and it is said to have antibiotic, anesthetic, and anti-inflammatory properties. Royal jelly is used to treat anemia, gastrointestinal ulcers, arteriosclerosis, hypo- and hypertension, and inhibition of sexual libido. Finally Bee bread, or bee pollen, is eaten as a generally health restorative, and is said to help treat both internal and external infections. All of these honey bee products are regularly produced and sold, especially online and in health food stores, though none are yet approved by the FDA.

Modern scientific uses

Though insects were widely used throughout history for medical treatment on nearly every continent, relatively little medical entomological research has been conducted since the revolutionary advent of antibiotics. Heavy reliance on antibiotics, coupled with discomfort with insects in Western culture limited the field of insect pharmacology until the rise of antibiotic resistant infections sparked pharmaceutical research to explore new resources. Arthropods represent a rich and largely unexplored source of new medicinal compounds.

Maggot therapy

Main article: Maggot therapy

Maggot therapy is the intentional introduction of live, disinfected blow fly larvae (maggots) into soft tissue wounds to selectively clean out the necrotic tissue. This helps to prevent infection; it also speeds healing of chronically infected wounds and ulcers. Military surgeons since classical antiquity noticed that wounds which had been left untreated for several days, and which had become infested with maggots, healed better than wounds not so infested. Maggots secrete several chemicals that kill microbes, including allantoin, urea, phenylacetic acid, phenylacetaldehyde, calcium carbonate, proteolytic enzymes, and many others.

Maggots were used for wound healing by the Maya and by indigenous Australians. More recently, they were used in Renaissance Europe, in the Napoleonic Wars, the American Civil War, and in the First and Second World Wars. It continues to be used in military medicine.

Apitherapy

Main article: Apitherapy

Apitherapy is the medical use of honeybee products such as honey, pollen, bee bread, propolis, royal jelly and bee venom. One of the major peptides in bee venom, called Melittin, has the potential to treat inflammation in sufferers of Rheumatoid arthritis and Multiple sclerosis. Melittin blocks the expression of inflammatory genes, thus reducing swelling and pain. It is administered by direct insect sting, or intramuscular injections. Bee products demonstrate a wide array of antimicrobial factors and in laboratory studies and have been shown to kill antibiotic resistant bacteria, pancreatic cancer cells, and many other infectious microbes.

Blister beetle and Spanish fly

Main article: Spanish fly

Spanish fly is an emerald-green beetle, Lytta vesicatoria, in the blister beetle family (Meloidae). It and other such species were used in preparations offered by traditional apothecaries. The insect is the source of the terpenoid cantharidin, a toxic blistering agent once used as an aphrodisiac.

Blood-feeding insects

Many blood-feeding insects like ticks, horseflies, and mosquitoes inject multiple bioactive compounds into their prey. These insects have been used by practitioners of Eastern Medicine for hundreds of years to prevent blood clot formation or thrombosis. However, modern medical research has only recently begun to investigate the drug development potential of blood-feeding insect saliva. These compounds in the saliva of blood feeding insects are capable of increasing the ease of blood feeding by preventing coagulation of platelets around the wound and provide protection against the host's immune response. Currently, over 1280 different protein families have been associated with the saliva of blood feeding organisms. This diverse range of compounds may include:

• inhibitors of platelet aggregation, ADP, arachidonic acid, thrombin, and PAF.
• anticoagulants
• vasodilators
• vasoconstrictors
• antihistamines
• sodium channel blockers
• complement inhibitors
• pore formers
• inhibitors of angiogenesis
• anaesthetics
• AMPs and microbial pattern recognition molecules.
• Parasite enhancers/activators

Currently, some preliminary progress has been made with investigation of the therapeutic properties of tick anticoagulant peptide (TAP) and Ixolaris a novel recombinant tissue factor pathway inhibitor (TFPI) from the salivary gland of the tick, Ixodes scapularis. Additionally, Ixolaris, a tissue factor inhibitor has been shown to block primary tumor growth and angiogenesis in a glioblastoma model. Despite the strong potential of these compounds for use as anticoagulants or immunomodulating drugs no modern medicines, developed from the saliva of blood-sucking insects, are currently on the market.

Arachnids

Like plants and insects, arachnids have also been used for thousands of years in traditional medical practices. Recent scientific research in natural bioactive factors has increased, leading to a renewed interest in venom components in many animals. In 1993 Margatoxin was synthesized from the venom of the Centruroides margaritatus the Central American bark scorpion. It is a peptide that selectively inhibits voltage-dependent potassium channels. Patented by Merck, it has the potential to prevent neointimal hyperplasia, a common cause of bypass graft failure.

In addition to medical uses of arachnid defense compounds, a great amount of research has recently been directed toward the synthesis and use of spider silk as a scaffolding for ligament generation. Spider silk is an ideal material for the synthesis of medical skin grafts or ligament implants because it is one of the strongest known natural fibers and triggers little immune response in animals. Spider silk may also be used to make fine sutures for stitching nerves or eyes to heal with little scarring. Medical uses of spider silk is not a new idea. Spider silks have been used for thousands of years to fight infection and heal wounds. Efforts to produce industrial quantities and qualities of spider silk in transgenic goat milk are underway.

Psychoactive scorpions

Recent news reports claim that use of scorpions for psychoactive purposes is gaining in popularity in Asia. Heroin addicts in Afghanistan are purported to smoke dried scorpions or use scorpion stings to get high when heroin is not available. The use of scorpions as a psychoactive drug reportedly gives an instant high as strong or stronger than heroin. However, there is little information on the long-term effects of using scorpion toxins. The 'scorpion sting craze' has also increased in India with a decreasing availability of other drugs and alcohol available to youth. Young people are reportedly flocking to highway sides where they can purchase scorpion stings that after several minutes of intense pain, supposedly produce a six- to eight-hour feeling of wellbeing.

Linear independence

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Linear_independence

Linearly independent vectors in ${\displaystyle \mathbb {R} ^{3}}$

Linearly dependent vectors in a plane in ${\displaystyle \mathbb {R} ^{3}.}$

In the theory of vector spaces, a set of vectors is said to be linearly dependent if there is a nontrivial linear combination of the vectors that equals the zero vector. If no such linear combination exists, then the vectors are said to be linearly independent. These concepts are central to the definition of dimension.

A vector space can be of finite dimension or infinite dimension depending on the maximum number of linearly independent vectors. The definition of linear dependence and the ability to determine whether a subset of vectors in a vector space is linearly dependent are central to determining the dimension of a vector space.

Definition

A sequence of vectors ${\displaystyle \mathbf {v} _{1},\mathbf {v} _{2},\dots ,\mathbf {v} _{k}}$ from a vector space V is said to be linearly dependent, if there exist scalars ${\displaystyle a_{1},a_{2},\dots ,a_{k},}$ not all zero, such that

${\displaystyle a_{1}\mathbf {v} _{1}+a_{2}\mathbf {v} _{2}+\cdots +a_{k}\mathbf {v} _{k}=\mathbf {0} ,}$

where ${\displaystyle \mathbf {0} }$ denotes the zero vector.

This implies that at least one of the scalars is nonzero, say ${\displaystyle a_{1}\neq 0}$, and the above equation can be written as

${\displaystyle \mathbf {v} _{1}={\frac {-a_{2}}{a_{1}}}\mathbf {v} _{2}+\cdots +{\frac {-a_{k}}{a_{1}}}\mathbf {v} _{k},}$

if ${\displaystyle k>1,}$ and ${\displaystyle \mathbf {v} _{1}=\mathbf {0} }$ if ${\displaystyle k=0.}$

Thus, a set of vectors is linearly dependent if and only if one of them is zero or a linear combination of the others.

A sequence of vectors ${\displaystyle \mathbf {v} _{1},\mathbf {v} _{2},\dots ,\mathbf {v} _{n}}$ is said to be linearly independent if it is not linearly dependent, that is, if the equation

${\displaystyle a_{1}\mathbf {v} _{1}+a_{2}\mathbf {v} _{2}+\cdots +a_{n}\mathbf {v} _{n}=\mathbf {0} ,}$

can only be satisfied by ${\displaystyle a_{i}=0}$ for ${\displaystyle i=1,\dots ,n.}$ This implies that no vector in the sequence can be represented as a linear combination of the remaining vectors in the sequence. In other words, a sequence of vectors is linearly independent if the only representation of ${\displaystyle \mathbf {0} }$ as a linear combination of its vectors is the trivial representation in which all the scalars ${\displaystyle a_{i}}$ are zero. Even more concisely, a sequence of vectors is linearly independent if and only if ${\displaystyle \mathbf {0} }$ can be represented as a linear combination of its vectors in a unique way.

If a sequence of vectors contains the same vector twice, it is necessarily dependent. The linear dependency of a sequence of vectors does not depend of the order of the terms in the sequence. This allows defining linear independence for a finite set of vectors: A finite set of vectors is linearly independent if the sequence obtained by ordering them is linearly independent. In other words, one has the following result that is often useful.

A sequence of vectors is linearly independent if and only if it does not contain the same vector twice and the set of its vectors is linearly independent.

Infinite case

An infinite set of vectors is linearly independent if every nonempty finite subset is linearly independent. Conversely, an infinite set of vectors is linearly dependent if it contains a finite subset that is linearly dependent, or equivalently, if some vector in the set is a linear combination of other vectors in the set.

An indexed family of vectors is linearly independent if it does not contain the same vector twice, and if the set of its vectors is linearly independent. Otherwise, the family is said linearly dependent.

A set of vectors which is linearly independent and spans some vector space, forms a basis for that vector space. For example, the vector space of all polynomials in x over the reals has the (infinite) subset {1, x, x², ...} as a basis.

Geometric examples

• ${\displaystyle {\vec {u}}}$ and ${\displaystyle {\vec {v}}}$ are independent and define the plane P.
• ${\displaystyle {\vec {u}}}$, ${\displaystyle {\vec {v}}}$ and ${\displaystyle {\vec {w}}}$ are dependent because all three are contained in the same plane.
• ${\displaystyle {\vec {u}}}$ and ${\displaystyle {\vec {j}}}$ are dependent because they are parallel to each other.
• ${\displaystyle {\vec {u}}}$ , ${\displaystyle {\vec {v}}}$ and ${\displaystyle {\vec {k}}}$ are independent because ${\displaystyle {\vec {u}}}$ and ${\displaystyle {\vec {v}}}$ are independent of each other and ${\displaystyle {\vec {k}}}$ is not a linear combination of them or, equivalently, because they do not belong to a common plane. The three vectors define a three-dimensional space.
• The vectors ${\displaystyle {\vec {o}}}$ (null vector, whose components are equal to zero) and ${\displaystyle {\vec {k}}}$ are dependent since ${\displaystyle {\vec {o}}=0{\vec {k}}}$

Geographic location

A person describing the location of a certain place might say, "It is 3 miles north and 4 miles east of here." This is sufficient information to describe the location, because the geographic coordinate system may be considered as a 2-dimensional vector space (ignoring altitude and the curvature of the Earth's surface). The person might add, "The place is 5 miles northeast of here." This last statement is true, but it is not necessary to find the location.

In this example the "3 miles north" vector and the "4 miles east" vector are linearly independent. That is to say, the north vector cannot be described in terms of the east vector, and vice versa. The third "5 miles northeast" vector is a linear combination of the other two vectors, and it makes the set of vectors linearly dependent, that is, one of the three vectors is unnecessary to define a specific location on a plane.

Also note that if altitude is not ignored, it becomes necessary to add a third vector to the linearly independent set. In general, n linearly independent vectors are required to describe all locations in n-dimensional space.

Evaluating linear independence

The zero vector

If one or more vectors from a given sequence of vectors ${\displaystyle \mathbf {v} _{1},\dots ,\mathbf {v} _{k}}$ is the zero vector ${\displaystyle \mathbf {0} }$ then the vector ${\displaystyle \mathbf {v} _{1},\dots ,\mathbf {v} _{k}}$ are necessarily linearly dependent (and consequently, they are not linearly independent). To see why, suppose that ${\displaystyle i}$ is an index (i.e. an element of ${\displaystyle \{1,\ldots ,k\}}$) such that ${\displaystyle \mathbf {v} _{i}=\mathbf {0} .}$ Then let ${\displaystyle a_{i}:=1}$ (alternatively, letting ${\displaystyle a_{i}}$ be equal any other non-zero scalar will also work) and then let all other scalars be ${\displaystyle 0}$ (explicitly, this means that for any index ${\displaystyle j}$ other than ${\displaystyle i}$ (i.e. for ${\displaystyle j\neq i}$), let ${\displaystyle a_{j}:=0}$ so that consequently ${\displaystyle a_{j}\mathbf {v} _{j}=0\mathbf {v} _{j}=\mathbf {0} }$). Simplifying ${\displaystyle a_{1}\mathbf {v} _{1}+\cdots +a_{k}\mathbf {v} _{k}}$ gives:

${\displaystyle a_{1}\mathbf {v} _{1}+\cdots +a_{k}\mathbf {v} _{k}=\mathbf {0} +\cdots +\mathbf {0} +a_{i}\mathbf {v} _{i}+\mathbf {0} +\cdots +\mathbf {0} =a_{i}\mathbf {v} _{i}=a_{i}\mathbf {0} =\mathbf {0} .}$

Because not all scalars are zero (in particular, ${\displaystyle a_{i}\neq 0}$), this proves that the vectors ${\displaystyle \mathbf {v} _{1},\dots ,\mathbf {v} _{k}}$ are linearly dependent.

As a consequence, the zero vector can not possibly belong to any collection of vectors that is linearly independent.

Now consider the special case where the sequence of ${\displaystyle \mathbf {v} _{1},\dots ,\mathbf {v} _{k}}$ has length ${\displaystyle 1}$ (i.e. the case where ${\displaystyle k=1}$). A collection of vectors that consists of exactly one vector is linearly dependent if and only if that vector is zero. Explicitly, if ${\displaystyle \mathbf {v} _{1}}$ is any vector then the sequence ${\displaystyle \mathbf {v} _{1}}$ (which is a sequence of length ${\displaystyle 1}$) is linearly dependent if and only if ${\displaystyle \mathbf {v} _{1}=\mathbf {0} }$; alternatively, the collection ${\displaystyle \mathbf {v} _{1}}$ is linearly independent if and only if ${\displaystyle \mathbf {v} _{1}\neq \mathbf {0} .}$

Linear dependence and independence of two vectors

This example considers the special case where there are exactly two vector ${\displaystyle \mathbf {u} }$ and ${\displaystyle \mathbf {v} }$ from some real or complex vector space. The vectors ${\displaystyle \mathbf {u} }$ and ${\displaystyle \mathbf {v} }$ are linearly dependent if and only if at least one of the following is true:

1. ${\displaystyle \mathbf {u} }$ is a scalar multiple of ${\displaystyle \mathbf {v} }$ (explicitly, this means that there exists a scalar ${\displaystyle c}$ such that ${\displaystyle \mathbf {u} =c\mathbf {v} }$) or
2. ${\displaystyle \mathbf {v} }$ is a scalar multiple of ${\displaystyle \mathbf {u} }$ (explicitly, this means that there exists a scalar ${\displaystyle c}$ such that ${\displaystyle \mathbf {v} =c\mathbf {u} }$).

If ${\displaystyle \mathbf {u} =\mathbf {0} }$ then by setting ${\displaystyle c:=0}$ we have ${\displaystyle c\mathbf {v} =0\mathbf {v} =\mathbf {0} =\mathbf {u} }$ (this equality holds no matter what the value of ${\displaystyle \mathbf {v} }$ is), which shows that (1) is true in this particular case. Similarly, if ${\displaystyle \mathbf {v} =\mathbf {0} }$ then (2) is true because ${\displaystyle \mathbf {v} =0\mathbf {u} .}$ If ${\displaystyle \mathbf {u} =\mathbf {v} }$ (for instance, if they are both equal to the zero vector ${\displaystyle \mathbf {0} }$) then both (1) and (2) are true (by using ${\displaystyle c:=1}$ for both).

If ${\displaystyle \mathbf {u} =c\mathbf {v} }$ then ${\displaystyle \mathbf {u} \neq \mathbf {0} }$ is only possible if ${\displaystyle c\neq 0}$ and ${\displaystyle \mathbf {v} \neq \mathbf {0} }$; in this case, it is possible to multiply both sides by ${\textstyle {\frac {1}{c}}}$ to conclude ${\textstyle \mathbf {v} ={\frac {1}{c}}\mathbf {u} .}$ This shows that if ${\displaystyle \mathbf {u} \neq \mathbf {0} }$ and ${\displaystyle \mathbf {v} \neq \mathbf {0} }$ then (1) is true if and only if (2) is true; that is, in this particular case either both (1) and (2) are true (and the vectors are linearly dependent) or else both (1) and (2) are false (and the vectors are linearly independent). If ${\displaystyle \mathbf {u} =c\mathbf {v} }$ but instead ${\displaystyle \mathbf {u} =\mathbf {0} }$ then at least one of ${\displaystyle c}$ and ${\displaystyle \mathbf {v} }$ must be zero. Moreover, if exactly one of ${\displaystyle \mathbf {u} }$ and ${\displaystyle \mathbf {v} }$ is ${\displaystyle \mathbf {0} }$ (while the other is non-zero) then exactly one of (1) and (2) is true (with the other being false).

The vectors ${\displaystyle \mathbf {u} }$ and ${\displaystyle \mathbf {v} }$ are linearly independent if and only if ${\displaystyle \mathbf {u} }$ is not a scalar multiple of ${\displaystyle \mathbf {v} }$ and ${\displaystyle \mathbf {v} }$ is not a scalar multiple of ${\displaystyle \mathbf {u} }$.

Vectors in R²

Three vectors: Consider the set of vectors ${\displaystyle \mathbf {v} _{1}=(1,1),}$ ${\displaystyle \mathbf {v} _{2}=(-3,2),}$ and ${\displaystyle \mathbf {v} _{3}=(2,4),}$ then the condition for linear dependence seeks a set of non-zero scalars, such that

${\displaystyle a_{1}{\begin{bmatrix}1\\1\end{bmatrix}}+a_{2}{\begin{bmatrix}-3\\2\end{bmatrix}}+a_{3}{\begin{bmatrix}2\\4\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}},}$

or

${\displaystyle {\begin{bmatrix}1&-3&2\\1&2&4\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}.}$

Row reduce this matrix equation by subtracting the first row from the second to obtain,

${\displaystyle {\begin{bmatrix}1&-3&2\\0&5&2\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}.}$

Continue the row reduction by (i) dividing the second row by 5, and then (ii) multiplying by 3 and adding to the first row, that is

${\displaystyle {\begin{bmatrix}1&0&16/5\\0&1&2/5\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}.}$

Rearranging this equation allows us to obtain

${\displaystyle {\begin{bmatrix}1&0\\0&1\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\end{bmatrix}}={\begin{bmatrix}a_{1}\\a_{2}\end{bmatrix}}=-a_{3}{\begin{bmatrix}16/5\\2/5\end{bmatrix}}.}$

which shows that non-zero a_i exist such that ${\displaystyle \mathbf {v} _{3}=(2,4)}$ can be defined in terms of ${\displaystyle \mathbf {v} _{1}=(1,1)}$ and ${\displaystyle \mathbf {v} _{2}=(-3,2).}$ Thus, the three vectors are linearly dependent.

Two vectors: Now consider the linear dependence of the two vectors ${\displaystyle \mathbf {v} _{1}=(1,1)}$ and ${\displaystyle \mathbf {v} _{2}=(-3,2),}$ and check,

${\displaystyle a_{1}{\begin{bmatrix}1\\1\end{bmatrix}}+a_{2}{\begin{bmatrix}-3\\2\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}},}$

or

${\displaystyle {\begin{bmatrix}1&-3\\1&2\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}.}$

The same row reduction presented above yields,

${\displaystyle {\begin{bmatrix}1&0\\0&1\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}.}$

This shows that ${\displaystyle a_{i}=0,}$ which means that the vectors v₁ = (1, 1) and v₂ = (−3, 2) are linearly independent.

Vectors in R⁴

In order to determine if the three vectors in ${\displaystyle \mathbb {R} ^{4},}$

${\displaystyle \mathbf {v} _{1}={\begin{bmatrix}1\\4\\2\\-3\end{bmatrix}},\mathbf {v} _{2}={\begin{bmatrix}7\\10\\-4\\-1\end{bmatrix}},\mathbf {v} _{3}={\begin{bmatrix}-2\\1\\5\\-4\end{bmatrix}}.}$

are linearly dependent, form the matrix equation,

${\displaystyle {\begin{bmatrix}1&7&-2\\4&10&1\\2&-4&5\\-3&-1&-4\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}}={\begin{bmatrix}0\\0\\0\\0\end{bmatrix}}.}$

Row reduce this equation to obtain,

${\displaystyle {\begin{bmatrix}1&7&-2\\0&-18&9\\0&0&0\\0&0&0\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}}={\begin{bmatrix}0\\0\\0\\0\end{bmatrix}}.}$

Rearrange to solve for v₃ and obtain,

${\displaystyle {\begin{bmatrix}1&7\\0&-18\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\end{bmatrix}}=-a_{3}{\begin{bmatrix}-2\\9\end{bmatrix}}.}$

This equation is easily solved to define non-zero a_i,

${\displaystyle a_{1}=-3a_{3}/2,a_{2}=a_{3}/2,}$

where ${\displaystyle a_{3}}$ can be chosen arbitrarily. Thus, the vectors ${\displaystyle \mathbf {v} _{1},\mathbf {v} _{2},}$ and ${\displaystyle \mathbf {v} _{3}}$ are linearly dependent.

Alternative method using determinants

An alternative method relies on the fact that ${\displaystyle n}$ vectors in ${\displaystyle \mathbb {R} ^{n}}$ are linearly independent if and only if the determinant of the matrix formed by taking the vectors as its columns is non-zero.

In this case, the matrix formed by the vectors is

${\displaystyle A={\begin{bmatrix}1&-3\\1&2\end{bmatrix}}.}$

We may write a linear combination of the columns as

${\displaystyle A\Lambda ={\begin{bmatrix}1&-3\\1&2\end{bmatrix}}{\begin{bmatrix}\lambda _{1}\\\lambda _{2}\end{bmatrix}}.}$

We are interested in whether AΛ = 0 for some nonzero vector Λ. This depends on the determinant of ${\displaystyle A}$, which is

${\displaystyle \det A=1\cdot 2-1\cdot (-3)=5\neq 0.}$

Since the determinant is non-zero, the vectors ${\displaystyle (1,1)}$ and ${\displaystyle (-3,2)}$ are linearly independent.

Otherwise, suppose we have ${\displaystyle m}$ vectors of ${\displaystyle n}$ coordinates, with ${\displaystyle m<n.}$ Then A is an n×m matrix and Λ is a column vector with ${\displaystyle m}$ entries, and we are again interested in AΛ = 0. As we saw previously, this is equivalent to a list of ${\displaystyle n}$ equations. Consider the first ${\displaystyle m}$ rows of ${\displaystyle A}$, the first ${\displaystyle m}$ equations; any solution of the full list of equations must also be true of the reduced list. In fact, if ⟨i₁,...,i_m⟩ is any list of ${\displaystyle m}$ rows, then the equation must be true for those rows.

${\displaystyle A_{\langle i_{1},\dots ,i_{m}\rangle }\Lambda =\mathbf {0} .}$

Furthermore, the reverse is true. That is, we can test whether the ${\displaystyle m}$ vectors are linearly dependent by testing whether

${\displaystyle \det A_{\langle i_{1},\dots ,i_{m}\rangle }=0}$

for all possible lists of ${\displaystyle m}$ rows. (In case ${\displaystyle m=n}$, this requires only one determinant, as above. If ${\displaystyle m>n}$, then it is a theorem that the vectors must be linearly dependent.) This fact is valuable for theory; in practical calculations more efficient methods are available.

More vectors than dimensions

If there are more vectors than dimensions, the vectors are linearly dependent. This is illustrated in the example above of three vectors in ${\displaystyle \mathbb {R} ^{2}.}$

Natural basis vectors

Let ${\displaystyle V=\mathbb {R} ^{n}}$ and consider the following elements in ${\displaystyle V}$, known as the natural basis vectors:

${\displaystyle {\begin{matrix}\mathbf {e} _{1}&=&(1,0,0,\ldots ,0)\\\mathbf {e} _{2}&=&(0,1,0,\ldots ,0)\\&\vdots \\\mathbf {e} _{n}&=&(0,0,0,\ldots ,1).\end{matrix}}}$

Then ${\displaystyle \mathbf {e} _{1},\mathbf {e} _{2},\ldots ,\mathbf {e} _{n}}$ are linearly independent.

Proof

Suppose that ${\displaystyle a_{1},a_{2},\ldots ,a_{n}}$ are real numbers such that

${\displaystyle a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+\cdots +a_{n}\mathbf {e} _{n}=\mathbf {0} .}$

Since

${\displaystyle a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+\cdots +a_{n}\mathbf {e} _{n}=\left(a_{1},a_{2},\ldots ,a_{n}\right),}$

then ${\displaystyle a_{i}=0}$ for all ${\displaystyle i=1,\ldots ,n.}$

Linear independence of functions

Let ${\displaystyle V}$ be the vector space of all differentiable functions of a real variable ${\displaystyle t}$. Then the functions ${\displaystyle e^{t}}$ and ${\displaystyle e^{2t}}$ in ${\displaystyle V}$ are linearly independent.

Proof

Suppose ${\displaystyle a}$ and ${\displaystyle b}$ are two real numbers such that

${\displaystyle ae^{t}+be^{2t}=0}$

Take the first derivative of the above equation:

${\displaystyle ae^{t}+2be^{2t}=0}$

for all values of ${\displaystyle t.}$ We need to show that ${\displaystyle a=0}$ and ${\displaystyle b=0.}$ In order to do this, we subtract the first equation from the second, giving ${\displaystyle be^{2t}=0}$. Since ${\displaystyle e^{2t}}$ is not zero for some ${\displaystyle t}$, ${\displaystyle b=0.}$ It follows that ${\displaystyle a=0}$ too. Therefore, according to the definition of linear independence, ${\displaystyle e^{t}}$ and ${\displaystyle e^{2t}}$ are linearly independent.

Space of linear dependencies

A linear dependency or linear relation among vectors v₁, ..., v_n is a tuple (a₁, ..., a_n) with n scalar components such that

${\displaystyle a_{1}\mathbf {v} _{1}+\cdots +a_{n}\mathbf {v} _{n}=\mathbf {0} .}$

If such a linear dependence exists with at least a nonzero component, then the n vectors are linearly dependent. Linear dependencies among v₁, ..., v_n form a vector space.

If the vectors are expressed by their coordinates, then the linear dependencies are the solutions of a homogeneous system of linear equations, with the coordinates of the vectors as coefficients. A basis of the vector space of linear dependencies can therefore be computed by Gaussian elimination.

Generalizations

Affine independence

See also: Affine space

A set of vectors is said to be affinely dependent if at least one of the vectors in the set can be defined as an affine combination of the others. Otherwise, the set is called affinely independent. Any affine combination is a linear combination; therefore every affinely dependent set is linearly dependent. Conversely, every linearly independent set is affinely independent.

Consider a set of ${\displaystyle m}$ vectors ${\displaystyle \mathbf {v} _{1},\ldots ,\mathbf {v} _{m}}$ of size ${\displaystyle n}$ each, and consider the set of ${\displaystyle m}$ augmented vectors ${\textstyle \left(\left[{\begin{smallmatrix}1\\\mathbf {v} _{1}\end{smallmatrix}}\right],\ldots ,\left[{\begin{smallmatrix}1\\\mathbf {v} _{m}\end{smallmatrix}}\right]\right)}$ of size ${\displaystyle n+1}$ each. The original vectors are affinely independent if and only if the augmented vectors are linearly independent.

Linearly independent vector subspaces

Two vector subspaces ${\displaystyle M}$ and ${\displaystyle N}$ of a vector space ${\displaystyle X}$ are said to be linearly independent if ${\displaystyle M\cap N=\{0\}.}$ More generally, a collection ${\displaystyle M_{1},\ldots ,M_{d}}$ of subspaces of ${\displaystyle X}$ are said to be linearly independent if ${\textstyle M_{i}\cap \sum _{k\neq i}M_{k}=\{0\}}$ for every index ${\displaystyle i,}$ where ${\textstyle \sum _{k\neq i}M_{k}={\Big \{}m_{1}+\cdots +m_{i-1}+m_{i+1}+\cdots +m_{d}:m_{k}\in M_{k}{\text{ for all }}k{\Big \}}=\operatorname {span} \bigcup _{k\in \{1,\ldots ,i-1,i+1,\ldots ,d\}}M_{k}.}$ The vector space ${\displaystyle X}$ is said to be a direct sum of ${\displaystyle M_{1},\ldots ,M_{d}}$ if these subspaces are linearly independent and ${\displaystyle M_{1}+\cdots +M_{d}=X.}$