Apr 9
Original link: https://medium.com/@rakviashvili95/quantum-logic-gates-e6dd84ece00f
Quantum logic gates
INTRODUCTION
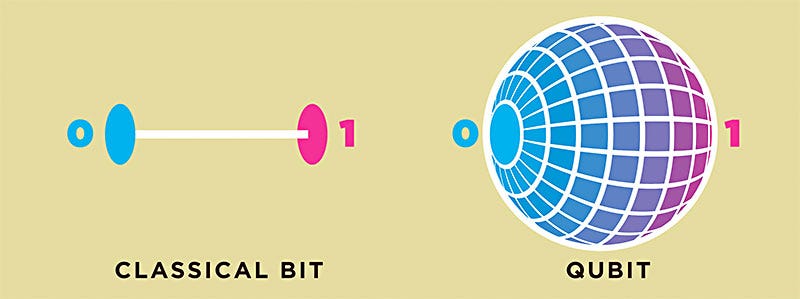
Traditional computers are like microscopic cities. The roads of these cities are wires with electricity coursing through them. These roads have lots of gates, known as logic gates, which enable computers to do their job. Like physical gates that allow or block cars, logic gates allow or block electricity. Electricity that goes through the gates represents a “1” of digital data, and blocked electricity is a “0”. Like this, in quantum world there is quantum bits(aka qubit) and quantum gates. In quantum computing the information is encoded in qubits.
A qubit is a two-level quantum system where the two basis qubit states are usually written as |0⟩ (“|⟩” represent Dirac notation) and |1⟩. A qubit can be in state |0⟩, |1⟩ or (unlike a classical bit) in a linear combination of both states. For example one qubit vector presentation is:
|ψ⟩ = α|0⟩ + β|1⟩
where ψ is a qubit and (α, β) is a two-dimensional complex vector with a length of one(also they are complex probability amplitudes).
The name of this phenomenon is superposition.
Unlike many classical logic gates, quantum logic gates are reversible(it means that if I tell you the operation I did and the output of that operation, you can always tell the input of that operation).
SINGLE QUBIT QUANTUM GATES
Now let’s talk about quantum gates which works only with one qubit input value. Now we will use vector representation of |0⟩ and |1⟩.

Hadamard gate(H)
Mathematically Hadamard gate is 2x2 matrix:
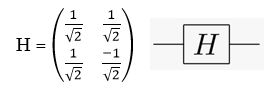
The Hadamard gate acts on a single qubit. It maps the basic states |0⟩ and |1⟩ into exactly equal superposition.
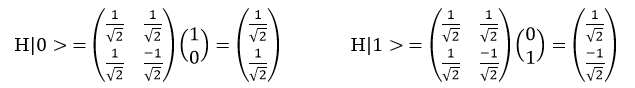
The Hadamard gate also takes a qubit in exactly-equal superposition, and transforms it into a |0⟩ or|1⟩-bit

Remember operations are their own inverse!
Pauli gates (X, Y , Z)
The Pauli gates (X, Y, Z) are the three Pauli matrixes and act on single qubit. The Pauli-X gate is the quantum equivalent of the NOT gate for classical computers with respect to the standard basis |0⟩ and |1⟩. It is sometimes called a bit-flip as it maps |0⟩ to |1⟩ and |1⟩ to |0⟩.

Similarly, the Pauli-Y maps |0⟩ to i|1⟩ and |1⟩ to -i|0⟩.

The Pauli-Z leaves the basic state |0⟩ unchanged and maps |1⟩ to -|1⟩. Due to this nature, the Pauli-Z is sometimes called phase-flip.

The Pauli matrices are involutory, meaning that the square of a Pauli matrix is the identity matrix.

Phase gate (S)
It acts on one qubit, leaves unchanged |0⟩ and transforms |1⟩ into i|1⟩

DOUBLE QUBIT QUANTUM GATES
Before we start working on double quantum gates, we should mention tensor product of two vectors. The tensor product is used to combine quantum states. The combined state of two qubits is the tensor product of two qubits. It is denoted as ⊗, and looks like this:

Controlled NOT gate(CNOT)
One of the most important two-bit logic elements is the controllable NOT gate.

If the first qubit is in the |0⟩ state, then it does not change the second qubit, and if the first qubit is in the |1⟩ state, then it changes the value of the second, converting zero to one and vice versa.

SWAP gate
It acts on 2 qubits and leaves |00⟩ and |11⟩ unchanged and |01⟩ moves to |10⟩ and vice versa

TRIPLE QUBIT QUANTUM GATES
Toffoli gate(CCNOT)
The Toffoli element operates on 3 qubits, it is also called a controlled-controlled NOT (CCNOT) gate. It is universal (universal is an element that can perform any logical function without the help of other elements) for classical calculations but not for quantum computations. He leaves everything up to three cubits unchanged and alone |110⟩ moves to |111⟩ and vice versa. Its matrix will be written like this:

EXTRA: CIRCUIT COMPOSITION
Serially wired gates
Assume that we have two gates A and B, that both act on n qubits. When B is put after A in a series circuit, then the effect of the two gates can be described as a single gate C.
C = B * A
where * is matrix multiplication. The resulting gate C will have the same dimensions as A and B. The order in which the gates would appear in a circuit diagram is reversed when multiplying them together.
For example, putting the Pauli-X gate after the Pauli-Y gate, both of which act on a single qubit, can be described as a single combined gate C:


Parallel wired gates
When connected in parallel, these gates will give you a tensor product. If we connect Paul-Y gate to Paul-X gate in parallel then we get that:

and formula for it will be:


