From Wikipedia, the free encyclopedia
Power stations may be located near a fuel source, at a dam site, or to take advantage of renewable energy sources, and are often located away from heavily populated areas. They are usually quite large to take advantage of the economies of scale. The electric power which is generated is stepped up to a higher voltage at which it connects to the electric power transmission network.
The bulk power transmission network will move the power long distances, sometimes across international boundaries, until it reaches its wholesale customer (usually the company that owns the local electric power distribution network).
On arrival at a substation, the power will be stepped down from a transmission level voltage to a distribution level voltage. As it exits the substation, it enters the distribution wiring. Finally, upon arrival at the service location, the power is stepped down again from the distribution voltage to the required service voltage(s).
Term
The term grid usually refers to a network, and should not be taken to imply a particular physical layout or a breadth. Grid may also be used to refer to an entire continent's electrical network, a regional transmission network or may be used to describe a subnetwork such as a local utility's transmission grid or distribution grid.
History
Since its inception in the Industrial Age, the electrical grid has evolved from an insular system that serviced a particular geographic area to a wider, expansive network that incorporated multiple areas. At one point, all energy was produced near the device or service requiring that energy. In the early 19th century, electricity was a novel invention that competed with steam, hydraulics, direct heating and cooling, light, and most notably gas. During this period, gas production and delivery had become the first centralized element in the modern energy industry. It was first produced on customer’s premises but later evolved into large gasifiers that enjoyed economies of scale. Virtually every city in the U.S. and Europe had town gas piped through their municipalities as it was a dominant form of household energy use. By the mid-19th century, electric arc lighting soon became advantageous compared to volatile gas lamps since gas lamps produced poor light, tremendous wasted heat which made rooms hot and smoky, and noxious elements in the form of hydrogen and carbon monoxide. Modeled after the gas lighting industry, the first electric utility systems supplied energy through virtual mains to light filtration as opposed to gas burners. With this, electric utilities also took advantage of economies of scale and moved to centralized power generation, distribution, and system management.[2]With the realization of long distance power transmission it was possible to interconnect different central stations to balance loads and improve load factors. Interconnection became increasingly desirable as electrification grew rapidly in the early years of the 20th century. Like telegraphy before it, wired electricity was often carried on and through the circuits of colonial rule.[3]
Charles Merz, of the Merz & McLellan consulting partnership, built the Neptune Bank Power Station near Newcastle upon Tyne in 1901,[4] and by 1912 had developed into the largest integrated power system in Europe.[5] In 1905 he tried to influence Parliament to unify the variety of voltages and frequencies in the country's electricity supply industry, but it was not until World War I that Parliament began to take this idea seriously, appointing him head of a Parliamentary Committee to address the problem. In 1916 Merz pointed out that the UK could use its small size to its advantage, by creating a dense distribution grid to feed its industries efficiently. His findings led to the Williamson Report of 1918, which in turn created the Electricity Supply Bill of 1919. The bill was the first step towards an integrated electricity system.
The more significant Electricity (Supply) Act of 1926 led to the setting up of the National Grid.[6] The Central Electricity Board standardised the nation's electricity supply and established the first synchronised AC grid, running at 132 kilovolts and 50 Hertz. This started operating as a national system, the National Grid, in 1938.
In the United States in the 1920s, utilities joined together establishing a wider utility grid as joint-operations saw the benefits of sharing peak load coverage and backup power. Also, electric utilities were easily financed by Wall Street private investors who backed many of their ventures. In 1934, with the passage of the Public Utility Holding Company Act (USA), electric utilities were recognized as public goods of importance along with gas, water, and telephone companies and thereby were given outlined restrictions and regulatory oversight of their operations. This ushered in the Golden Age of Regulation for more than 60 years. However, with the successful deregulation of airlines and telecommunication industries in late 1970s, the Energy Policy Act (EPAct) of 1992 advocated deregulation of electric utilities by creating wholesale electric markets. It required transmission line owners to allow electric generation companies open access to their network.[2][7] The act led to a major restructuring of how the electric industry operated in an effort to create competition in power generation. No longer were electric utilities built as vertical monopolies, where generation, transmission and distribution were handled by a single company. Now, the three stages could be split among various companies, in an effort to provide fair accessibility to high voltage transmission.[8] In 2005, the Energy Policy Act of 2005 was passed to allow incentives and loan guarantees for alternative energy production and advance innovative technologies that avoided greenhouse emissions.
Features
The wide area synchronous grids of Europe. Most are members of the European Transmission System Operators association.
The Continental U.S. power transmission grid consists of about 300,000 km of lines operated by approximately 500 companies. The North American Electric Reliability Corporation (NERC) oversees all of them.
High-voltage direct current interconnections in western Europe - red are existing links, green are under construction, and blue are proposed.
Structure of distribution grids
The structure, or "topology" of a grid can vary considerably. The physical layout is often forced by what land is available and its geology. The logical topology can vary depending on the constraints of budget, requirements for system reliability, and the load and generation characteristics.The cheapest and simplest topology for a distribution or transmission grid is a radial structure. This is a tree shape where power from a large supply radiates out into progressively lower voltage lines until the destination homes and businesses are reached.
Most transmission grids require the reliability that more complex mesh networks provide. If one were to imagine running redundant lines between limbs/branches of a tree that could be turned in case any particular limb of the tree were severed, then this image approximates how a mesh system operates. The expense of mesh topologies restrict their application to transmission and medium voltage distribution grids. Redundancy allows line failures to occur and power is simply rerouted while workmen repair the damaged and deactivated line.
Other topologies used are looped systems found in Europe and tied ring networks.
In cities and towns of North America, the grid tends to follow the classic radially fed design. A substation receives its power from the transmission network, the power is stepped down with a transformer and sent to a bus from which feeders fan out in all directions across the countryside. These feeders carry three-phase power, and tend to follow the major streets near the substation. As the distance from the substation grows, the fan out continues as smaller laterals spread out to cover areas missed by the feeders. This tree-like structure grows outward from the substation, but for reliability reasons, usually contains at least one unused backup connection to a nearby substation. This connection can be enabled in case of an emergency, so that a portion of a substation's service territory can be alternatively fed by another substation.
Geography of transmission networks
Transmission networks are more complex with redundant pathways. For example, see the map of the United States' (right) high-voltage transmission network.A wide area synchronous grid or "interconnection" is a group of distribution areas all operating with alternating current (AC) frequencies synchronized (so that peaks occur at the same time). This allows transmission of AC power throughout the area, connecting a large number of electricity generators and consumers and potentially enabling more efficient electricity markets and redundant generation. Interconnection maps are shown of North America (right) and Europe (below left).
In a synchronous grid all the generators run not only at the same frequency but also at the same phase, each generator maintained by a local governor that regulates the driving torque by controlling the steam supply to the turbine driving it. Generation and consumption must be balanced across the entire grid, because energy is consumed almost instantaneously as it is produced. Energy is stored in the immediate short term by the rotational kinetic energy of the generators.
A large failure in one part of the grid - unless quickly compensated for - can cause current to re-route itself to flow from the remaining generators to consumers over transmission lines of insufficient capacity, causing further failures. One downside to a widely connected grid is thus the possibility of cascading failure and widespread power outage. A central authority is usually designated to facilitate communication and develop protocols to maintain a stable grid. For example, the North American Electric Reliability Corporation gained binding powers in the United States in 2006, and has advisory powers in the applicable parts of Canada and Mexico. The U.S. government has also designated National Interest Electric Transmission Corridors, where it believes transmission bottlenecks have developed.
Some areas, for example rural communities in Alaska, do not operate on a large grid, relying instead on local diesel generators.[9]
High-voltage direct current lines or variable frequency transformers can be used to connect two alternating current interconnection networks which are not synchronized with each other. This provides the benefit of interconnection without the need to synchronize an even wider area. For example, compare the wide area synchronous grid map of Europe (above left) with the map of HVDC lines (below right).
Redundancy and defining "grid"
A town is only said to have achieved grid connection when it is connected to several redundant sources, generally involving long-distance transmission.This redundancy is limited. Existing national or regional grids simply provide the interconnection of facilities to utilize whatever redundancy is available. The exact stage of development at which the supply structure becomes a grid is arbitrary. Similarly, the term national grid is something of an anachronism in many parts of the world, as transmission cables now frequently cross national boundaries. The terms distribution grid for local connections and transmission grid for long-distance transmissions are therefore preferred, but national grid is often still used for the overall structure.
Interconnected Grid
Electric utilities across regions are many times interconnected for improved economy and reliability. Interconnections allow for economies of scale, allowing energy to be purchased from large, efficient sources. Utilities can draw power from generator reserves from a different region in order to ensure continuing, reliable power and diversify their loads. Interconnection also allows regions to have access to cheap bulk energy by receiving power from different sources. For example, one region may be producing cheap hydro power during high water seasons, but in low water seasons, another area may be producing cheaper power through wind, allowing both regions to access cheaper energy sources from one another during different times of the year. Neighboring utilities also help others to maintain the overall system frequency and also help manage tie transfers between utility regions.[8]Aging Infrastructure
Despite the novel institutional arrangements and network designs of the electrical grid, its power delivery infrastructures suffer aging across the developed world. Four contributing factors to the current state of the electric grid and its consequences are:- Aging power equipment – older equipment has higher failure rates, leading to customer interruption rates affecting the economy and society; also, older assets and facilities lead to higher inspection maintenance costs and further repair/restoration costs.
- Obsolete system layout – older areas require serious additional substation sites and rights-of-way that cannot be obtained in current area and are forced to use existing, insufficient facilities.
- Outdated engineering – traditional tools for power delivery planning and engineering are ineffective in addressing current problems of aged equipment, obsolete system layouts, and modern deregulated loading levels.
- Old cultural value – planning, engineering, operating of system using concepts and procedures that worked in vertically integrated industry exacerbate the problem under a deregulated industry [10]
Modern trends
As the 21st century progresses, the electric utility industry seeks to take advantage of novel approaches to meet growing energy demand. Utilities are under pressure to evolve their classic topologies to accommodate distributed generation. As generation becomes more common from rooftop solar and wind generators, the differences between distribution and transmission grids will continue to blur. Also, demand response is a grid management technique where retail or wholesale customers are requested either electronically or manually to reduce their load. Currently, transmission grid operators use demand response to request load reduction from major energy users such as industrial plants.[11]With everything interconnected, and open competition occurring in a free market economy, it starts to make sense to allow and even encourage distributed generation (DG). Smaller generators, usually not owned by the utility, can be brought on-line to help supply the need for power. The smaller generation facility might be a home-owner with excess power from their solar panel or wind turbine. It might be a small office with a diesel generator. These resources can be brought on-line either at the utility's behest, or by owner of the generation in an effort to sell electricity. Many small generators are allowed to sell electricity back to the grid for the same price they would pay to buy it. Furthermore, numerous efforts are underway to develop a "smart grid". In the U.S., the Energy Policy Act of 2005 and Title XIII of the Energy Independence and Security Act of 2007 are providing funding to encourage smart grid development. The hope is to enable utilities to better predict their needs, and in some cases involve consumers in some form of time-of-use based tariff. Funds have also been allocated to develop more robust energy control technologies.[12][13]
Various planned and proposed systems to dramatically increase transmission capacity are known as super, or mega grids. The promised benefits include enabling the renewable energy industry to sell electricity to distant markets, the ability to increase usage of intermittent energy sources by balancing them across vast geological regions, and the removal of congestion that prevents electricity markets from flourishing. Local opposition to siting new lines and the significant cost of these projects are major obstacles to super grids. One study for a European super grid estimates that as much as 750 GW of extra transmission capacity would be required- capacity that would be accommodated in increments of 5 GW HVDC lines. A recent proposal by Transcanada priced a 1,600-km, 3-GW HVDC line at $3 billion USD and would require a corridor wide. In India, a recent 6 GW, 1,850-km proposal was priced at $790 million and would require a wide right of way. With 750 GW of new HVDC transmission capacity required for a European super grid, the land and money needed for new transmission lines would be considerable.
Future trends
As deregulation continues further, utilities are driven to sell their assets as the energy market follows in line with the gas market in use of the futures and spot markets and other financial arrangements. Even globalization with foreign purchases are taking place. One such purchase was the when UK’s National Grid, the largest private electric utility in the world, bought New England’s electric system for $3.2 billion.[14] Also, Scottish Power purchased Pacific Energy for $12.8 billion.[citation needed] Domestically, local electric and gas firms have merged operations as they saw the advantages of joint affiliation, especially with the reduced cost of joint-metering. Technological advances will take place in the competitive wholesale electric markets, such examples already being utilized include fuel cells used in space flight; aeroderivative gas turbines used in jet aircraft; solar engineering and photovoltaic systems; off-shore wind farms; and the communication advances spawned by the digital world, particularly with microprocessing which aids in monitoring and dispatching.[2]Electricity is expected to see growing demand in the future. The Information Revolution is highly reliant on electric power. Other growth areas include emerging new electricity-exclusive technologies, developments in space conditioning, industrial processes, and transportation (for example hybrid vehicles, locomotives).[2]
Emerging smart grid
As mentioned above, the electrical grid is expected to evolve to a new grid paradigm—smart grid, an enhancement of the 20th century electrical grid. The traditional electrical grids are generally used to carry power from a few central generators to a large number of users or customers. In contrast, the new emerging smart grid uses two-way flows of electricity and information to create an automated and distributed advanced energy delivery network.Many research projects have been conducted to explore the concept of smart grid. According to a newest survey on smart grid,[15] the research is mainly focused on three systems in smart grid- the infrastructure system, the management system, and the protection system.
The infrastructure system is the energy, information, and communication infrastructure underlying of the smart grid that supports 1) advanced electricity generation, delivery, and consumption; 2) advanced information metering, monitoring, and management; and 3) advanced communication technologies. In the transition from the conventional power grid to smart grid, we will replace a physical infrastructure with a digital one. The needs and changes present the power industry with one of the biggest challenges it has ever faced.
A smart grid would allow the power industry to observe and control parts of the system at higher resolution in time and space.[16] It would allow for customers to obtain cheaper, greener, less intrusive, more reliable and higher quality power from the grid. The legacy grid did not allow for real time information to be relayed from the grid, so one of the main purposes of the smart grid would be to allow real time information to be received and sent from and to various parts of the grid to make operation as efficient and seamless as possible. It would allow us to manage logistics of the grid and view consequences that arise from its operation on a time scale with high resolution; from high-frequency switching devices on a microsecond scale, to wind and solar output variations on a minute scale, to the future effects of the carbon emissions generated by power production on a decade scale.
The management system is the subsystem in smart grid that provides advanced management and control services. Most of the existing works aim to improve energy efficiency, demand profile, utility, cost, and emission, based on the infrastructure by using optimization, machine learning, and game theory. Within the advanced infrastructure framework of smart grid, more and more new management services and applications are expected to emerge and eventually revolutionize consumers' daily lives.
The protection system is the subsystem in smart grid that provides advanced grid reliability analysis, failure protection, and security and privacy protection services. We must note that the advanced infrastructure used in smart grid on one hand empowers us to realize more powerful mechanisms to defend against attacks and handle failures, but on the other hand, opens up many new vulnerabilities. For example, National Institute of Standards and Technology pointed out that the major benefit provided by smart grid, the ability to get richer data to and from customer smart meters and other electric devices, is also its Achilles' heel from a privacy viewpoint. The obvious privacy concern is that the energy use information stored at the meter acts as an information rich side channel. This information could be mined and retrieved by interested parties to reveal personal information such as individual's habits, behaviors, activities, and even beliefs.













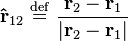 is the
is the 




 is a closed surface and
is a closed surface and  is the mass enclosed by the surface.
is the mass enclosed by the surface. and total mass
and total mass  ,
,


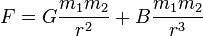 , B a constant
, B a constant (Laplace)
(Laplace) (Decombes)
(Decombes)