Roche limit

From Wikipedia, the free encyclopedia

 

This article is about the distance within which an orbiting object will form rings. For the limits at which an orbiting object will be captured, see Roche lobe. For the gravitational sphere of influence of one astronomical body in the face of perturbations from another heavier body around which it orbits, see Roche sphere.

 

An orbiting mass of fluid held together by gravity, here viewed from above the orbital plane. Far from the Roche limit the mass is practically spherical.  

Closer to the Roche limit the body is deformed by tidal forces.  

Within the Roche limit the mass's own gravity can no longer withstand the tidal forces, and the body disintegrates.  

Particles closer to the primary move more quickly than particles farther away, as represented by the red arrows.  

The varying orbital speed of the material eventually causes it to form a ring.

In celestial mechanics, the Roche limit, also called Roche radius, is the distance in which a celestial body, held together only by its own gravity, will disintegrate due to a second celestial body's tidal forces exceeding the first body's gravitational self-attraction.^[1] Inside the Roche limit, orbiting material disperses and forms rings whereas outside the limit material tends to coalesce. The term is named after Édouard Roche (pronounced [ʁɔʃ] (French), /rɔːʃ/ rawsh (English)), who is the French astronomer who first calculated this theoretical limit in 1848.^[2]

Explanation

Comet Shoemaker-Levy 9 was disintegrated by the tidal forces of Jupiter into a string of smaller bodies in 1992, before colliding with the planet in 1994.

Typically, the Roche limit applies to a satellite's disintegrating due to tidal forces induced by its primary, the body about which it orbits. Parts of the satellite that are closer to the primary are attracted more strongly by gravity from the primary than parts that are farther away; this disparity effectively pulls the near and far parts of the satellite apart from each other, and if the disparity (combined with any centrifugal effects due to the object's spin) is larger than the force of gravity holding the satellite together, it can pull the satellite apart. Some real satellites, both natural and artificial, can orbit within their Roche limits because they are held together by forces other than gravitation. Objects resting on the surface of such a satellite would be lifted away by tidal forces. A weaker satellite, such as a comet, could be broken up when it passes within its Roche limit.

Since, within the Roche limit, tidal forces overwhelm the gravitational forces that might otherwise hold the satellite together, no satellite can gravitationally coalesce out of smaller particles within that limit. Indeed, almost all known planetary rings are located within their Roche limit, Saturn's E-Ring and Phoebe ring being notable exceptions. They could either be remnants from the planet's proto-planetary accretion disc that failed to coalesce into moonlets, or conversely have formed when a moon passed within its Roche limit and broke apart.

The Roche limit is not the only factor that causes comets to break apart. Splitting by thermal stress, internal gas pressure and rotational splitting are other ways for a comet to split under stress.

Selected examples

The table below shows the mean density and the equatorial radius for selected objects in the Solar System.

Primary	Density (kg/m3)	Radius (m)
Sun	1,408	696,000,000
Earth	5,513	6,378,137
Moon	3,346	1,737,100
Jupiter	1,326	71,493,000
Saturn	687	60,267,000
Uranus	1,318	25,557,000
Neptune	1,638	24,766,000

The equations for the Roche limits relate the minimum sustainable orbital radius to the ratio of the two objects' densities and the Radius of the primary body. Hence, using the data above, the Roche limits for these objects can be calculated. This has been done twice for each, assuming the extremes of the rigid and fluid body cases. The average density of comets is taken to be around 500 kg/m³.

The table below gives the Roche limits expressed in kilometres and in primary radii. The mean radius of the orbit can be compared with the Roche limits. For convenience, the table lists the mean radius of the orbit for each, excluding the comets, whose orbits are extremely variable and eccentric.

Body	Satellite	Roche limit (rigid)		Roche limit (fluid)		Mean orbital radius (km)
		Distance (km)	R	Distance (km)	R
Earth	Moon	9,492	1.49	18,381	2.88	384,399
Earth	average comet	17,887	2.80	34,638	5.43	N/A
Sun	Earth	556,397	0.80	1,077,467	1.55	149,597,890
Sun	Jupiter	894,677	1.29	1,732,549	2.49	778,412,010
Sun	Moon	657,161	0.94	1,272,598	1.83	149,597,890 Approx
Sun	average comet	1,238,390	1.78	2,398,152	3.45	N/A

These bodies are well outside their Roche limits by various factors, from 21 for the Moon (over its fluid-body Roche limit) as part of the Earth–Moon system, upwards to hundreds for Earth and Jupiter.

The table below gives each satellite's closest approach in its orbit divided by its own Roche limit. Again, both rigid and fluid body calculations are given. Note that Pan, Cordelia and Naiad, in particular, may be quite close to their actual break-up points.

In practice, the densities of most of the inner satellites of giant planets are not known. In these cases, shown in italics, likely values have been assumed, but their actual Roche limit can vary from the value shown.

Primary	Satellite	Orbital Radius / Roche limit
		(rigid)	(fluid)
Sun	Mercury	104:1	54:1
Earth	Moon	41:1	21:1
Mars	Phobos	172%	89%
	Deimos	451%	234%
Jupiter	Metis	~186%	~94%
	Adrastea	~188%	~95%
	Amalthea	175%	88%
	Thebe	254%	128%
Saturn	Pan	142%	70%
	Atlas	156%	78%
	Prometheus	162%	80%
	Pandora	167%	83%
	Epimetheus	200%	99%
	Janus	195%	97%
Uranus	Cordelia	~154%	~79%
	Ophelia	~166%	~86%
	Bianca	~183%	~94%
	Cressida	~191%	~98%
	Desdemona	~194%	~100%
	Juliet	~199%	~102%
Neptune	Naiad	~139%	~72%
	Thalassa	~145%	~75%
	Despina	~152%	~78%
	Galatea	153%	79%
	Larissa	~218%	~113%
Pluto	Charon	12.5:1	6.5:1

Determination

The limiting distance to which a satellite can approach without breaking up depends on the rigidity of the satellite. At one extreme, a completely rigid satellite will maintain its shape until tidal forces break it apart. At the other extreme, a highly fluid satellite gradually deforms leading to increased tidal forces, causing the satellite to elongate, further compounding the tidal forces and causing it to break apart more readily.

Most real satellites would lie somewhere between these two extremes, with tensile strength rendering the satellite neither perfectly rigid nor perfectly fluid. For example, a rubble-pile asteroid will behave more like a fluid than a solid rocky one; an icy body will behave quite rigidly at first but become more fluid as tidal heating accumulates and its ices begin to melt.

But note that, as defined above, the Roche limit refers to a body held together solely by the gravitational forces which cause otherwise unconnected particles to coalesce, thus forming the body in question. The Roche limit is also usually calculated for the case of a circular orbit, although it is straightforward to modify the calculation to apply to the case (for example) of a body passing the primary on a parabolic or hyperbolic trajectory.

Rigid-satellite calculation

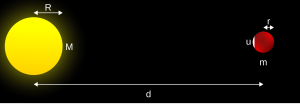
The rigid-body Roche limit is a simplified calculation for a spherical satellite. Irregular shapes such as those of tidal deformation on the body or the primary it orbits are neglected. It is assumed to be in hydrostatic equilibrium. These assumptions, although unrealistic, greatly simplify calculations.

The Roche limit for a rigid spherical satellite is the distance, ${\displaystyle d}$, from the primary at which the gravitational force on a test mass at the surface of the object is exactly equal to the tidal force pulling the mass away from the object:^[3][4]

${\displaystyle d=R_{M}\left(2{\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}}$

where ${\displaystyle R_{M}}$ is the radius of the primary, ${\displaystyle \rho _{M}}$ is the density of the primary, and ${\displaystyle \rho _{m}}$ is the density of the satellite. This can be equivalently written as

${\displaystyle d=R_{m}\left(2{\frac {M_{M}}{M_{m}}}\right)^{\frac {1}{3}}}$

where ${\displaystyle R_{m}}$ is the radius of the secondary, ${\displaystyle M_{M}}$ is the mass of the primary, and ${\displaystyle M_{m}}$ is the mass of the secondary.

This does not depend on the size of the objects, but on the ratio of densities. This is the orbital distance inside of which loose material (e.g. regolith) on the surface of the satellite closest to the primary would be pulled away, and likewise material on the side opposite the primary will also be pulled away from, rather than toward, the satellite.

Note that this is an approximate result as inertia force and rigid structure are ignored in its derivation.

Derivation of the formula

Derivation of the Roche limit

In order to determine the Roche limit, consider a small mass ${\displaystyle u}$ on the surface of the satellite closest to the primary. There are two forces on this mass ${\displaystyle u}$: the gravitational pull towards the satellite and the gravitational pull towards the primary. Assume that the satellite is in free fall around the primary and that the tidal force is the only relevant term of the gravitational attraction of the primary. This assumption is a simplification as free-fall only truly applies to the planetary center, but will suffice for this derivation.^[5]

The gravitational pull ${\displaystyle F_{\text{G}}}$ on the mass ${\displaystyle u}$ towards the satellite with mass ${\displaystyle m}$ and radius ${\displaystyle r}$ can be expressed according to Newton's law of gravitation.

${\displaystyle F_{\text{G}}={\frac {Gmu}{r^{2}}}}$

the tidal force ${\displaystyle F_{\text{T}}}$ on the mass ${\displaystyle u}$ towards the primary with radius ${\displaystyle R}$ and mass ${\displaystyle M}$, at a distance ${\displaystyle d}$ between the centers of the two bodies, can be expressed approximately as

${\displaystyle F_{\text{T}}={\frac {2GMur}{d^{3}}}}$.

To obtain this approximation, find the difference in the primary's gravitational pull on the center of the satellite and on the edge of the satellite closest to the primary:

${\displaystyle F_{\text{T}}={\frac {GMu}{(d-r)^{2}}}-{\frac {GMu}{d^{2}}}}$

${\displaystyle F_{\text{T}}=GMu{\frac {d^{2}-(d-r)^{2}}{d^{2}(d-r)^{2}}}}$

${\displaystyle F_{\text{T}}=GMu{\frac {2dr-r^{2}}{d^{4}-2d^{3}r+r^{2}d^{2}}}}$

In the approximation where ${\displaystyle r\ll R}$ and ${\displaystyle R$, it can be said that the ${\displaystyle r^{2}}$ in the numerator and every term with ${\displaystyle r}$ in the denominator goes to zero, which gives us:

${\displaystyle F_{\text{T}}=GMu{\frac {2dr}{d^{4}}}}$

${\displaystyle F_{\text{T}}={\frac {2GMur}{d^{3}}}}$

The Roche limit is reached when the gravitational force and the tidal force balance each other out.

${\displaystyle F_{\text{G}}=F_{\text{T}}\;}$

or

${\displaystyle {\frac {Gmu}{r^{2}}}={\frac {2GMur}{d^{3}}}}$,

which gives the Roche limit, ${\displaystyle d}$, as

${\displaystyle d=r\left(2\,{\frac {M}{m}}\right)^{\frac {1}{3}}}$

The radius of the satellite should not appear in the expression for the limit, so it is re-written in terms of densities.

For a sphere the mass ${\displaystyle M}$ can be written as

${\displaystyle M={\frac {4\pi \rho _{M}R^{3}}{3}}}$ where ${\displaystyle R}$ is the radius of the primary.

And likewise

${\displaystyle m={\frac {4\pi \rho _{m}r^{3}}{3}}}$ where ${\displaystyle r}$ is the radius of the satellite.

Substituting for the masses in the equation for the Roche limit, and cancelling out ${\displaystyle 4\pi /3}$ gives

${\displaystyle d=r\left({\frac {2\rho _{M}R^{3}}{\rho _{m}r^{3}}}\right)^{1/3}}$,

which can be simplified to the Roche limit:

${\displaystyle d=R\left(2\,{\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}\approx 1.26R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}}$.

A more accurate formula

Since a close satellite will likely be orbiting in a nearly-circular orbit with synchronous rotation, consider how the centrifugal force from rotation will affect the results. That force is

${\displaystyle F_{C}=\omega ^{2}ur={\frac {GMur}{d^{3}}}}$

and it gets added to F_T. Doing the force-balance calculation yields this result for the Roche limit:

${\displaystyle d=R_{M}\left(3\;{\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}\approx 1.442R_{M}\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{\frac {1}{3}}}$ .......... (1)

or: ${\displaystyle d=R_{m}\left(3\;{\frac {M_{M}}{M_{m}}}\right)^{\frac {1}{3}}\approx 1.442\;R_{m}\left({\frac {M_{M}}{M_{m}}}\right)^{\frac {1}{3}}}$ .......... (2)

Use ${\displaystyle m={\frac {4\pi \rho _{m}r^{3}}{3}}}$ (where ${\displaystyle r}$ is the radius of the satellite) to replace ${\displaystyle \rho _{m}}$ in formula(1), we can have a third formula:

${\displaystyle d=\left({\frac {9M_{M}}{4\pi \rho _{m}}}\right)^{\frac {1}{3}}\approx 0.8947\left({\frac {M_{M}}{\rho _{m}}}\right)^{\frac {1}{3}}}$ .......... (3)

Thus, it is sufficient to observe the mass of the star (planet) and to estimate the density of the planet (satellite) to compute the Roche limit of the planet (satellite) in the stellar (planetary) system.

Roche limit, Hill sphere and radius of the planet

Consider a planet with a density of ${\displaystyle \rho _{m}}$ and a radius of ${\displaystyle r}$, orbiting a star with a mass of M in a distant of R,
Let's place the planet on its Roche limit: ${\displaystyle R_{\mathrm {Roche} }={\sqrt[{3}]{\frac {9M}{4\pi \rho _{m}}}}}$
Hill sphere of the planet here is around L1(or L2): ${\displaystyle R_{\mathrm {Hill} }=R_{\mathrm {Roche} }{\sqrt[{3}]{\frac {m}{3M}}}}$, Hill sphere ..........(4)
${\displaystyle l={\sqrt[{3}]{{\frac {9M}{4\pi \rho _{m}}}.{\frac {m}{3M}}}}=r}$

 the surface of the planet coincide with the Roche lobe(or the planet fill full the Roche lobe)!
Celestial body cannot absorb any little thing or further more, lose its material.This is the physical meaning of Roche limit, Roche lobe and Hill sphere.

Formula(2) can be described as: ${\displaystyle R_{\text{Roche}}=R_{\text{Hill}}{\sqrt[{3}]{\frac {3M}{m}}}=R_{\text{secondary}}{\sqrt[{3}]{\frac {3M}{m}}}}$, a perfect mathematical symmetry.

This is the astronomical significance of Roche limit and Hill sphere.

Fluid satellites

A more accurate approach for calculating the Roche limit takes the deformation of the satellite into account. An extreme example would be a tidally locked liquid satellite orbiting a planet, where any force acting upon the satellite would deform it into a prolate spheroid.

The calculation is complex and its result cannot be represented in an exact algebraic formula. Roche himself derived the following approximate solution for the Roche limit:

${\displaystyle d\approx 2.44R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{1/3}}$

However, a better approximation that takes into account the primary's oblateness and the satellite's mass is:

${\displaystyle d\approx 2.423R\left({\frac {\rho _{M}}{\rho _{m}}}\right)^{1/3}\left({\frac {(1+{\frac {m}{3M}})+{\frac {c}{3R}}(1+{\frac {m}{M}})}{1-c/R}}\right)^{1/3}}$

where ${\displaystyle c/R}$ is the oblateness of the primary. The numerical factor is calculated with the aid of a computer.

The fluid solution is appropriate for bodies that are only loosely held together, such as a comet. For instance, comet Shoemaker–Levy 9's decaying orbit around Jupiter passed within its Roche limit in July 1992, causing it to fragment into a number of smaller pieces. On its next approach in 1994 the fragments crashed into the planet. Shoemaker–Levy 9 was first observed in 1993, but its orbit indicated that it had been captured by Jupiter a few decades prior.^[6]

Derivation of the formula

As the fluid satellite case is more delicate than the rigid one, the satellite is described with some simplifying assumptions. First, assume the object consists of incompressible fluid that has constant density ${\displaystyle \rho _{m}}$ and volume ${\displaystyle V}$ that do not depend on external or internal forces.

Second, assume the satellite moves in a circular orbit and it remains in synchronous rotation. This means that the angular speed ${\displaystyle \omega }$ at which it rotates around its center of mass is the same as the angular speed at which it moves around the overall system barycenter.

The angular speed ${\displaystyle \omega }$ is given by Kepler's third law:

${\displaystyle \omega ^{2}=G\,{\frac {M+m}{d^{3}}}.}$

When M is very much bigger than m, this will be close to

${\displaystyle \omega ^{2}=G\,{\frac {M}{d^{3}}}.}$

The synchronous rotation implies that the liquid does not move and the problem can be regarded as a static one. Therefore, the viscosity and friction of the liquid in this model do not play a role, since these quantities would play a role only for a moving fluid.

Given these assumptions, the following forces should be taken into account:

• The force of gravitation due to the main body;
• the centrifugal force in the rotary reference system; and
• the self-gravitation field of the satellite.

Since all of these forces are conservative, they can be expressed by means of a potential. Moreover, the surface of the satellite is an equipotential one. Otherwise, the differences of potential would give rise to forces and movement of some parts of the liquid at the surface, which contradicts the static model assumption. Given the distance from the main body, the form of the surface that satisfies the equipotential condition must be determined.

Radial distance of one point on the surface of the ellipsoid to the center of mass

As the orbit has been assumed circular, the total gravitational force and orbital centrifugal force acting on the main body cancel. That leaves two forces: the tidal force and the rotational centrifugal force. The tidal force depends on the position with respect to the center of mass, already considered in the rigid model. For small bodies, the distance of the liquid particles from the center of the body is small in relation to the distance d to the main body. Thus the tidal force can be linearized, resulting in the same formula for F_T as given above.

While this force in the rigid model depends only on the radius r of the satellite, in the fluid case, all the points on the surface must be considered, and the tidal force depends on the distance Δd from the center of mass to a given particle projected on the line joining the satellite and the main body. We call Δd the radial distance. Since the tidal force is linear in Δd, the related potential is proportional to the square of the variable and for ${\displaystyle m\ll M}$ we have

${\displaystyle V_{T}=-{\frac {3GM}{2d^{3}}}\Delta d^{2}\,}$

Likewise, the centrifugal force has a potential

${\displaystyle V_{C}=-{\frac {1}{2}}\omega ^{2}\Delta d^{2}=-{\frac {GM}{2d^{3}}}\Delta d^{2}\,}$

for rotational angular velocity ${\displaystyle \omega }$.

We want to determine the shape of the satellite for which the sum of the self-gravitation potential and V_T + V_C is constant on the surface of the body. In general, such a problem is very difficult to solve, but in this particular case, it can be solved by a skillful guess due to the square dependence of the tidal potential on the radial distance Δd To a first approximation, we can ignore the centrifugal potential V_C and consider only the tidal potential V_T.

Since the potential V_T changes only in one direction, i.e. the direction toward the main body, the satellite can be expected to take an axially symmetric form. More precisely, we may assume that it takes a form of a solid of revolution. The self-potential on the surface of such a solid of revolution can only depend on the radial distance to the center of mass. Indeed, the intersection of the satellite and a plane perpendicular to the line joining the bodies is a disc whose boundary by our assumptions is a circle of constant potential. Should the difference between the self-gravitation potential and V_T be constant, both potentials must depend in the same way on Δd. In other words, the self-potential has to be proportional to the square of Δd. Then it can be shown that the equipotential solution is an ellipsoid of revolution. Given a constant density and volume the self-potential of such body depends only on the eccentricity ε of the ellipsoid:

${\displaystyle V_{s}=V_{s_{0}}+G\pi \rho _{m}\cdot f(\epsilon )\cdot \Delta d^{2},}$

where ${\displaystyle V_{s_{0}}}$ is the constant self-potential on the intersection of the circular edge of the body and the central symmetry plane given by the equation Δd=0.

The dimensionless function f is to be determined from the accurate solution for the potential of the ellipsoid

${\displaystyle f(\epsilon )={\frac {1-\epsilon ^{2}}{\epsilon ^{3}}}\cdot \left[\left(3-\epsilon ^{2}\right)\cdot \operatorname {artanh} \epsilon -3\epsilon \right]}$

and, surprisingly enough, does not depend on the volume of the satellite.

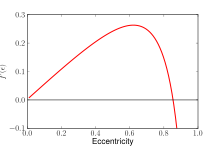
The graph of the dimensionless function f which indicates how the strength of the tidal potential depends on the eccentricity ε of the ellipsoid.

Although the explicit form of the function f looks complicated, it is clear that we may and do choose the value of ε so that the potential V_T is equal to V_S plus a constant independent of the variable Δd. By inspection, this occurs when

${\displaystyle {\frac {2G\pi \rho _{M}R^{3}}{d^{3}}}=G\pi \rho _{m}f(\epsilon )}$

This equation can be solved numerically. The graph indicates that there are two solutions and thus the smaller one represents the stable equilibrium form (the ellipsoid with the smaller eccentricity). This solution determines the eccentricity of the tidal ellipsoid as a function of the distance to the main body. The derivative of the function f has a zero where the maximal eccentricity is attained. This corresponds to the Roche limit.

The derivative of f determines the maximal eccentricity. This gives the Roche limit.

More precisely, the Roche limit is determined by the fact that the function f, which can be regarded as a nonlinear measure of the force squeezing the ellipsoid towards a spherical shape, is bounded so that there is an eccentricity at which this contracting force becomes maximal. Since the tidal force increases when the satellite approaches the main body, it is clear that there is a critical distance at which the ellipsoid is torn up.

The maximal eccentricity can be calculated numerically as the zero of the derivative of f'. One obtains

${\displaystyle \epsilon _{\text{max}}\approx 0{.}86}$

which corresponds to the ratio of the ellipsoid axes 1:1.95. Inserting this into the formula for the function f one can determine the minimal distance at which the ellipsoid exists. This is the Roche limit,

${\displaystyle d\approx 2{.}423\cdot R\cdot {\sqrt[{3}]{\frac {\rho _{M}}{\rho _{m}}}}\,.}$

Surprisingly, including the centrifugal potential makes remarkably little difference, though the object becomes a Roche ellipsoid, a general triaxial ellipsoid with all axes having different lengths. The potential becomes a much more complicated function of the axis lengths, requiring elliptic functions. However, the solution proceeds much as in the tidal-only case, and we find

${\displaystyle d\approx 2{.}455\cdot R\cdot {\sqrt[{3}]{\frac {\rho _{M}}{\rho _{m}}}}\,.}$

The ratios of polar to orbit-direction to primary-direction axes are 1:1.06:2.07.

Beam-powered propulsion

From Wikipedia, the free encyclopedia

Beam-powered propulsion, also known as directed energy propulsion, is a class of aircraft or spacecraft propulsion that uses energy beamed to the spacecraft from a remote power plant to provide energy. The beam is typically either a microwave or a laser beam and it is either pulsed or continuous. A continuous beam lends itself to thermal rockets, photonic thrusters and light sails, whereas a pulsed beam lends itself to ablative thrusters and pulse detonation engines.

The rule of thumb that is usually quoted is that it takes a megawatt of power beamed to a vehicle per kg of payload while it is being accelerated to permit it to reach low earth orbit.^[1]

Other than launching to orbit, applications for moving around the world quickly have also been proposed.

Background

Rockets are momentum machines; they use mass ejected from the rocket to provide momentum to the rocket. Momentum is the product of mass and velocity, so rockets generally attempt to put as much velocity into their working mass as possible, thereby minimizing the amount of working mass that is needed. In order to accelerate the working mass, energy is required. In a conventional rocket, the fuel is chemically combined to provide the energy, and the resulting fuel products, the ash or exhaust, are used as the working mass.

There is no particular reason why the same fuel has to be used for both energy and momentum. In the jet engine, for instance, the fuel is used only to produce energy, the working mass is provided from the air that the jet aircraft flies through. In modern jet engines, the amount of air propelled is much greater than the amount of air used for energy. This is not a solution for the rocket, however, as they quickly climb to altitudes where the air is too thin to be useful as a source of working mass.

Rockets can, however, carry their working mass and use some other source of energy. The problem is finding an energy source with a power-to-weight ratio that competes with chemical fuels. Small nuclear reactors can compete in this regard, and considerable work on nuclear thermal propulsion was carried out in the 1960s, but environmental concerns and rising costs led to the ending of most of these programs.

A further improvement can be made by removing the energy creation from the spacecraft. If the nuclear reactor is left on the ground and its energy transmitted to the spacecraft, the weight of the reactor is removed as well. The issue then is to get the energy into the spacecraft. This is the idea behind beamed power.

With beamed propulsion one can leave the power-source stationary on the ground, and directly (or via a heat exchanger) heat propellant on the spacecraft with a maser or a laser beam from a fixed installation. This permits the spacecraft to leave its power-source at home, saving significant amounts of mass, greatly improving performance.

Laser propulsion

Since a laser can heat propellant to extremely high temperatures, this potentially greatly improves the efficiency of a rocket, as exhaust velocity is proportional to the square root of the temperature. Normal chemical rockets have an exhaust speed limited by the fixed amount of energy in the propellants, but beamed propulsion systems have no particular theoretical limit (although in practice there are temperature limits).

Microwave propulsion

In microwave thermal propulsion, an external microwave beam is used to heat a refractory heat exchanger to >1,500 K, in turn heating a propellant such as hydrogen, methane or ammonia. This improves the specific impulse and thrust/weight ratio of the propulsion system relative to conventional rocket propulsion. For example, hydrogen can provide a specific impulse of 700–900 seconds and a thrust/weight ratio of 50-150.^[2]

A variation, developed by brothers James Benford and Gregory Benford, is to use thermal desorption of propellant trapped in the material of a very large microwave sail. This produces a very high acceleration compared to microwave pushed sails alone.

Electric propulsion

Some proposed spacecraft propulsion mechanisms use power in the form of electricity. Usually these schemes assume either solar panels, or an on-board reactor. However, both power sources are heavy.

Beamed propulsion in the form of laser can be used to send power to a photovoltaic panel, for Laser electric propulsion. In this system, careful design of the panels is necessary as the extra power tends to cause a fall-off of the conversion efficiency due to heating effects.

A microwave beam could be used to send power to a rectenna, for microwave electric propulsion. Microwave broadcast power has been practically demonstrated several times (e.g. Goldstone, California in 1974), rectennas are potentially lightweight and can handle high power at high conversion efficiency. However, rectennas tend to need to be very large for a significant amount of power to be captured.

Direct impulse

A beam could also be used to provide impulse by directly "pushing" on the sail.

One example of this would be using a solar sail to reflect a laser beam. This concept, called a laser-pushed lightsail, was initially proposed by Marx^[3] but first analyzed in detail, and elaborated on, by physicist Robert L. Forward in 1989^[4] as a method of Interstellar travel that would avoid extremely high mass ratios by not carrying fuel. Further analysis of the concept was done by Landis,^[5][6] Mallove and Matloff,^[7] Andrews^[8] and others.

In a later paper, Forward proposed pushing a sail with a microwave beam.^[9] This has the advantage that the sail need not be a continuous surface. Forward tagged his proposal for an ultralight sail "Starwisp". A later analysis by Landis^[10] suggested that the Starwisp concept as originally proposed by Forward would not work, but variations on the proposal continue to be proposed.

The beam has to have a large diameter so that only a small portion of the beam misses the sail due to diffraction and the laser or microwave antenna has to have a good pointing stability so that the craft can tilt its sails fast enough to follow the center of the beam. This gets more important when going from interplanetary travel to interstellar travel, and when going from a fly-by mission, to a landing mission, to a return mission. The laser or the microwave sender would probably be a large phased array of small devices, which get their energy directly from solar radiation. The size of the array negates the need for a lens or mirror.

Another beam-pushed concept would be to use a magnetic sail or MMPP sail to divert a beam of charged particles from a particle accelerator or plasma jet.^[11] Jordin Kare has proposed a variant to this whereby a "beam" of small laser accelerated light sails would transfer momentum to a magsail vehicle.

Another beam-pushed concept uses ordinary matter and works in vacuum. The matter from a stationary mass-driver is "reflected" by the spacecraft, cf. mass driver. The spacecraft neither needs energy nor reaction mass for propulsion of its own.

Proposed systems

Lightcraft

A lightcraft is a vehicle currently under development that uses an external pulsed source of laser or maser energy to provide power for producing thrust.

The laser shines on a parabolic reflector on the underside of the vehicle that concentrates the light to produce a region of extremely high temperature. The air in this region is heated and expands violently, producing thrust with each pulse of laser light. In space, a lightcraft would need to provide this gas itself from onboard tanks or from an ablative solid. By leaving the vehicle's power source on the ground and by using ambient atmosphere as reaction mass for much of its ascent, a lightcraft would be capable of delivering a very large percentage of its launch mass to orbit. It could also potentially be very cheap to manufacture.

Testing

Early in the morning of 2 October 2000 at the High Energy Laser Systems Test Facility (HELSTF), Lightcraft Technologies, Inc. (LTI) with the help of Franklin B. Mead of the U.S. Air Force Research Laboratory and Leik Myrabo set a new world's altitude record of 233 feet (71 m) for its 4.8 inch (12.2 cm) diameter, 1.8-ounce (51 g), laser-boosted rocket in a flight lasting 12.7 seconds.^[12] Although much of the 8:35 am flight was spent hovering at 230+ feet, the Lightcraft earned a world record for the longest ever laser-powered free flight and the greatest "air time" (i.e., launch-to-landing/recovery) from a light-propelled object. This is comparable to Robert Goddard's first test flight of his rocket design. Increasing the laser power to 100 kilowatts will enable flights up to a 30-kilometer altitude. Their goal is to accelerate a one-kilogram microsatellite into low Earth orbit using a custom-built, one megawatt ground-based laser. Such a system would use just about 20 dollars' worth of electricity, placing launch costs per kilogram to many times less than current launch costs (which are measured in thousands of dollars).^{[citation needed]}

Myrabo's "lightcraft" design is a reflective funnel-shaped craft that channels heat from the laser, towards the center, using a reflective parabolic surface causing the laser to literally explode the air underneath it, generating lift. Reflective surfaces in the craft focus the beam into a ring, where it heats air to a temperature nearly five times hotter than the surface of the sun, causing the air to expand explosively for thrust.

Laser thermal rocket

A laser thermal rocket is a thermal rocket in which the propellant is heated by energy provided by an external laser beam.^[13][14] In 1992, Jordin Kare proposed a simpler, nearer term concept which has a rocket containing liquid hydrogen.^[15] The propellant is heated in a heat exchanger that the laser beam shines on before leaving the vehicle via a conventional nozzle. This concept can use continuous beam lasers, and the semiconductor lasers are now cost effective for this application.^[16][17]

Microwave thermal rocket

In 2002, Kevin L.G. Parkin proposed a similar system using microwaves.^{[2][18][19][20]} In May 2012, the DARPA/NASA Millimeter-wave Thermal Launch System (MTLS) Project began the first steps toward implementing this idea. The MTLS Project was the first to demonstrate a millimeter-wave absorbent refractory heat exchanger, subsequently integrating it into the propulsion system of a small rocket to produce the first millimeter-wave thermal rocket. Simultaneously, it developed the first high power cooperative target millimeter-wave beam director and used it to attempt the first millimeter-wave thermal rocket launch. Several launches were attempted but problems with the beam director could not be resolved before funding ran out in March 2014.

Economics

Motivation to develop beam-powered propulsion systems comes from the economic advantages that would be gained as a result of improved propulsion performance. In the case of beam-powered launch vehicles, better propulsion performance enables some combination of increased payload fraction, increased structural margins and fewer stages. JASON's 1977 study of laser propulsion,^[21] authored by Freeman Dyson, succinctly articulates the promise of beam-powered launch:

"Laser propulsion as an idea that may produce a revolution in space technology. A single laser facility on the ground can in theory launch single-stage vehicles into low or high earth orbit. The payload can be 20% or 30% of the vehicle take-off weight. It is far more economical in the use of mass and energy than chemical propulsion, and it is far more flexible in putting identical vehicles into a variety of orbits."

This promise was quantified in a 1978 Lockheed Study^[22] conducted for NASA:

"The results of the study showed that, with advanced technology, laser rocket system with either a space- or ground-based laser transmitter could reduce the national budget allocated to space transportation by 10 to 345 billion dollars over a 10-year life cycle when compared to advanced chemical propulsion systems (LO₂-LH₂) of equal capability."

Beam director cost

The 1970s-era studies and others since have cited beam director cost as a possible impediment to beam-powered launch systems. A recent cost-benefit analysis^[23] estimates that microwave (or laser) thermal rockets would be economical once beam director cost falls below 20 $/Watt. The current cost of suitable lasers is <100 and="" are="" att.="" att="" be="" beam="" cost="" current="" directors.="" for="" has="" in="" is="" lasers="" lowered="" magnetrons="" mass="" medical="" microwave="" of="" oven="" p="" production="" some="" sources="" suitable="" the="" these="" though="" thought="" to="" unsuitable="" use="">

Non-spacecraft applications

In 1964 William C. Brown demonstrated a miniature helicopter equipped with a combination antenna and rectifier device called a rectenna. The rectenna converted microwave power into electricity, allowing the helicopter to fly.^[24]

In 2002 a Japanese group propelled a tiny aluminium airplane by using a laser to vaporize a water droplet clinging to it, and in 2003 NASA researchers flew an 11-ounce (312 g) model airplane with a propeller powered with solar panels illuminated by a laser.^[25] It is possible that such beam-powered propulsion could be useful for long-duration high altitude unmanned aircraft or balloons, perhaps designed to serve – like satellites do today – as communication relays, science platforms, or surveillance platforms.

A "laser broom" has been proposed to sweep space debris from Earth orbit. This is another proposed use of beam-powered propulsion, used on objects that were not designed to be propelled by it, for example small pieces of scrap knocked off ("spalled") satellites. The technique works since the laser power ablates one side of the object, giving an impulse that changes the eccentricity of the object's orbit. The orbit would then intersect the atmosphere and burn up.

Why does CO2 cool the stratosphere & warm the troposphere? Warmists don't agree on an answer

Saturday, August 2, 2014

Exerpted from http://hockeyschtick.blogspot.com/2014/08/why-does-co2-cool-stratosphere-warm.html

 I have been searching for an explanation of a predicted mid-tropospheric "hot spot" which Anthropogenic Warming Theory has long touted as one result of theory.  Below is an excerpt from "The Hockey Schtick" blog which discusses this issue.  First however, note from the graphic above that this alleged hot spot still awaits detection, for whatever implications that may have for AGW theory.

---

 

A paper published today in the Journal of Climate uses "a chemistry-climate model coupled to an ocean model" to arrive at a number of seeming contradictory conclusions about the opposing radiative effects of the greenhouse gases CO2, water vapor, ozone, and halocarbons (CFCs) depending upon the levels in the atmosphere where each of these are present.

Conventional AGW theory proposes the existence of a mid-troposphere "hot spot" and an overlying cooling of the stratosphere because heat is "trapped" in the "hot spot" and therefore can't make it to the stratosphere. However, despite millions of weather balloon and satellite observations over the past 60 years, the "hot spot" has still not been found and thus questions the fundamental theory of anthropogenic global warming climate change. The formation of a "hot spot" would also require a physically impossible reduction of entropy in the mid-troposphere and thus violate the second law of thermodynamics which requires maximum entropy production. 

According to the abstract below, the net radiative effect of these greenhouse gases in the troposphere vs. tropopause vs. stratosphere are:

GHG                          troposphere        tropopause       stratosphere

CO2                          warming              warming            cooling
water vapor                      ?                   cooling              cooling
ozone                              ?                   warming            warming
CFCs                         warming                  ?                  cooling?

I've been asking CAGW believers for years why CO2 and other greenhouse gases have opposite radiative effects upon global temperatures depending upon where they happen to be located in the atmosphere, and have yet to receive a satisfactory answer. Even the warmists themselves can't seem to agree on this fundamental question underlying CAGW theory. Wikipedia propagandist William Connolley disagrees with Gavin Schmidt and RealClimate on why increased greenhouse gases would cause the stratosphere to cool. 

RealClimate links to this site (update: link broken, but this is a mirror site) for their explanation, which upon examination makes no sense, violates basic physics including the 1st and 2nd laws of thermodynamics and maximum entropy production, contains contradictions, and then concludes "We now know that stratospheric cooling and tropospheric warming are intimately connected and that carbon dioxide plays a part in both processes. At present, however, our understanding of stratospheric cooling is not complete and further research has to be done.":

Excerpt in blue text from the site Gavin & RealClimate claim has the definitive answer to the question "why does the stratosphere cool?" [emphasis added]:

Why does the stratosphere cool? There are several reasons why the stratosphere is cooling. The two best understood are: 1) depletion of stratospheric ozone 2) increase in atmospheric carbon dioxide Cooling due to ozone depletion The first effect is easy to understand. Less ozone leads to less absorption of ultra-violet radiation from the Sun. As a result, solar radiation is not converted into heat radiation in the stratosphere.  So cooling due to ozone depletion is simply reduced heating as a consequence of reduced absorption of ultra-violet radiation.  Ozone also acts as a greenhouse gas in the lower stratosphere.  Less ozone means less absorption of infra-red heat radiation and therefore less heat trapping. At an altitude of about 20 km, the effects of ultra-violet and infra-red radiation are about the same.  Ozone levels decrease the higher we go in the atmosphere but there are other greenhouse gases present in the air which we have to consider.

Cooling due to the greenhouse effect The second effect is more complicated. Greenhouse gases (CO2, O3, CFC) absorb infra-red radiation from the surface of the Earth and trap the heat in the troposphere.  If this absorption is really strong, the greenhouse gas blocks most of the outgoing infra-red radiation close to the Earth's surface.  This means that only a small amount of outgoing infra-red radiation reaches carbon dioxide in the upper troposphere and the lower stratosphere.  On the other hand, carbon dioxide emits heat radiation, which is lost from the stratosphere into space.  In the stratosphere, this emission of heat becomes larger than the energy  received from below by absorption and, as a result, there is a net energy loss from the stratosphere and a resulting cooling.  Other greenhouse gases, such as ozone and chlorofluorocarbons (CFC's), have a weaker impact because their concentrations in the troposphere are smaller. They do not entirely block the whole radiation in their wavelength regime so some reaches the stratosphere where it can be absorbed and, as a consequence, heat this region of the atmosphere. 3. Stratospheric cooling rates:  The picture shows how water, cabon dioxide and ozone contribute to longwave cooling in the stratosphere.   Colours from blue through red, yellow and to green show increasing cooling, grey areas show warming of the stratosphere.  The tropopause is shown as dotted line (the troposphere below and the stratosphere above).  For CO2 it is obvious that there is no cooling in the troposphere [or warming!], but a strong cooling effect in the stratosphere.  Ozone, on the other hand, cools the upper stratosphere but warms the lower stratosphere.  Figure from: Clough and Iacono, JGR, 1995; adapted from the SPARC Website.

Where does cooling take place? The impact of decreasing ozone concentrations is largest in the lower stratosphere, at an altitude of around 20 km, whereas increases in carbon dioxide lead to highest cooling at altitudes between 40 and 50 km (Figure 3).  All these different effects mean that some parts of the stratosphere are cooling more than others. 4. Cooling trends at different altitudes in the stratosphere.  source: Ramaswamy et al., Reviews of Geophysics, Feb. 2001

Other influences It is possible that greenhouse warming could disturb the heating of the Arctic stratosphere by changing planetary waves.  These waves are triggered by the surface structure in the Northern Hemisphere (mountain ranges like the Himalayas, or the alternation of land and sea).  Recent studies show that increases in the stratospheric water vapour concentration could also have a strong cooling effect, comparable to the effect of ozone loss. Conclusions We now know that stratospheric cooling and tropospheric warming are intimately connected and that carbon dioxide plays a part in both processes.  At present, however,  our understanding of stratospheric cooling is not complete and further research has to be done.  We do, however, already know that observed and predicted cooling in the stratosphere makes the formation of an Arctic ozone hole more likely.  [end excerpt] Note the quote above "In the stratosphere, this emission of heat [proper term is radiation] becomes larger than the energy received from below by absorption and, as a result, there is a net energy loss from the stratosphere and a resulting cooling." Basic physics question: How can CO2 increase emission of radiation to space if it is absorbing less radiation from below? This would violate the 1st law of thermodynamics which requires conservation of energy. Secondly, the graph above [from an AGW model] shows that CO2 greatly increases cooling of the stratosphere but has essentially zero effect warming or cooling on the troposphere [below the dotted line]. Therefore, this graph indicates a net cooling effect of CO2 upon the atmosphere. Therefore, can anyone please provide a plausible explanation that does not violate the laws of thermodynamics as to why increased CO2 allegedly warms the troposphere and cools the stratosphere? And why the model output above shows CO2 has a strong cooling effect in the stratosphere, but essentially zero warming or cooling effect in the troposphere? And if the stratosphere cools thus increasing the temperature gradient between troposphere and stratosphere, why that would not increase heat transfer from the troposphere to stratosphere (thus cooling the troposphere)?

Journal of Climate 2014 ; e-View

doi: http://dx.doi.org/10.1175/JCLI-D-14-00232.1