In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships among variables. It includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables (or 'predictors'). More specifically, regression analysis helps one understand how the typical value of the dependent variable (or 'criterion variable') changes when any one of the independent variables is varied, while the other independent variables are held fixed.
Most commonly, regression analysis estimates the conditional expectation of the dependent variable given the independent variables – that is, the average value of the dependent variable when the independent variables are fixed. Less commonly, the focus is on a quantile, or other location parameter of the conditional distribution of the dependent variable given the independent variables. In all cases, a function of the independent variables called the regression function is to be estimated. In regression analysis, it is also of interest to characterize the variation of the dependent variable around the prediction of the regression function using a probability distribution. A related but distinct approach is Necessary Condition Analysis[1] (NCA), which estimates the maximum (rather than average) value of the dependent variable for a given value of the independent variable (ceiling line rather than central line) in order to identify what value of the independent variable is necessary but not sufficient for a given value of the dependent variable.
Regression analysis is widely used for prediction and forecasting, where its use has substantial overlap with the field of machine learning. Regression analysis is also used to understand which among the independent variables are related to the dependent variable, and to explore the forms of these relationships. In restricted circumstances, regression analysis can be used to infer causal relationships between the independent and dependent variables. However this can lead to illusions or false relationships, so caution is advisable;[2] for example, correlation does not prove causation.
Many techniques for carrying out regression analysis have been developed. Familiar methods such as linear regression and ordinary least squares regression are parametric, in that the regression function is defined in terms of a finite number of unknown parameters that are estimated from the data. Nonparametric regression refers to techniques that allow the regression function to lie in a specified set of functions, which may be infinite-dimensional.
The performance of regression analysis methods in practice depends on the form of the data generating process, and how it relates to the regression approach being used. Since the true form of the data-generating process is generally not known, regression analysis often depends to some extent on making assumptions about this process. These assumptions are sometimes testable if a sufficient quantity of data is available. Regression models for prediction are often useful even when the assumptions are moderately violated, although they may not perform optimally. However, in many applications, especially with small effects or questions of causality based on observational data, regression methods can give misleading results.[3][4]
In a narrower sense, regression may refer specifically to the estimation of continuous response (dependent) variables, as opposed to the discrete response variables used in classification.[5] The case of a continuous dependent variable may be more specifically referred to as metric regression to distinguish it from related problems.[6]
History
The earliest form of regression was the method of least squares, which was published by Legendre in 1805,[7] and by Gauss in 1809.[8] Legendre and Gauss both applied the method to the problem of determining, from astronomical observations, the orbits of bodies about the Sun (mostly comets, but also later the then newly discovered minor planets). Gauss published a further development of the theory of least squares in 1821,[9] including a version of the Gauss–Markov theorem.The term "regression" was coined by Francis Galton in the nineteenth century to describe a biological phenomenon. The phenomenon was that the heights of descendants of tall ancestors tend to regress down towards a normal average (a phenomenon also known as regression toward the mean).[10][11] For Galton, regression had only this biological meaning,[12][13] but his work was later extended by Udny Yule and Karl Pearson to a more general statistical context.[14][15] In the work of Yule and Pearson, the joint distribution of the response and explanatory variables is assumed to be Gaussian. This assumption was weakened by R.A. Fisher in his works of 1922 and 1925.[16][17][18] Fisher assumed that the conditional distribution of the response variable is Gaussian, but the joint distribution need not be. In this respect, Fisher's assumption is closer to Gauss's formulation of 1821.
In the 1950s and 1960s, economists used electromechanical desk "calculators" to calculate regressions. Before 1970, it sometimes took up to 24 hours to receive the result from one regression.[19]
Regression methods continue to be an area of active research. In recent decades, new methods have been developed for robust regression, regression involving correlated responses such as time series and growth curves, regression in which the predictor (independent variable) or response variables are curves, images, graphs, or other complex data objects, regression methods accommodating various types of missing data, nonparametric regression, Bayesian methods for regression, regression in which the predictor variables are measured with error, regression with more predictor variables than observations, and causal inference with regression.
Regression models
Regression models involve the following parameters and variables:- The unknown parameters, denoted as
, which may represent a scalar or a vector.
- The independent variables,
.
- The dependent variable,
.
A regression model relates
 to a function of
to a function of  and
and  .
. . To carry out regression analysis, the form of the function
. To carry out regression analysis, the form of the function  must be specified. Sometimes the form of this function is based on knowledge about the relationship between
must be specified. Sometimes the form of this function is based on knowledge about the relationship between  and
and  that does not rely on the data. If no such knowledge is available, a flexible or convenient form for
that does not rely on the data. If no such knowledge is available, a flexible or convenient form for  is chosen.
is chosen.Assume now that the vector of unknown parameters
 is of length
is of length  . In order to perform a regression analysis the user must provide information about the dependent variable
. In order to perform a regression analysis the user must provide information about the dependent variable  :
:- If
data points of the form
are observed, where
, most classical approaches to regression analysis cannot be performed: since the system of equations defining the regression model is underdetermined, there are not enough data to recover
.
- If exactly
data points are observed, and the function
is linear, the equations
can be solved exactly rather than approximately. This reduces to solving a set of
equations with
unknowns (the elements of
, which has a unique solution as long as the
are linearly independent. If
is nonlinear, a solution may not exist, or many solutions may exist.
- The most common situation is where
data points are observed. In this case, there is enough information in the data to estimate a unique value for
that best fits the data in some sense, and the regression model when applied to the data can be viewed as an overdetermined system in
.
- Finding a solution for unknown parameters
that will, for example, minimize the distance between the measured and predicted values of the dependent variable
(also known as method of least squares).
- Under certain statistical assumptions, the regression analysis uses
the surplus of information to provide statistical information about the
unknown parameters
and predicted values of the dependent variable
.
Necessary number of independent measurements
Consider a regression model which has three unknown parameters, ,
,  , and
, and  . Suppose an experimenter performs 10 measurements all at exactly the same value of independent variable vector
. Suppose an experimenter performs 10 measurements all at exactly the same value of independent variable vector  (which contains the independent variables
(which contains the independent variables  ,
,  , and
, and  ).
In this case, regression analysis fails to give a unique set of
estimated values for the three unknown parameters; the experimenter did
not provide enough information. The best one can do is to estimate the
average value and the standard deviation of the dependent variable
).
In this case, regression analysis fails to give a unique set of
estimated values for the three unknown parameters; the experimenter did
not provide enough information. The best one can do is to estimate the
average value and the standard deviation of the dependent variable  . Similarly, measuring at two different values of
. Similarly, measuring at two different values of  would give enough data for a regression with two unknowns, but not for three or more unknowns.
would give enough data for a regression with two unknowns, but not for three or more unknowns.If the experimenter had performed measurements at three different values of the independent variable vector
 , then regression analysis would provide a unique set of estimates for the three unknown parameters in
, then regression analysis would provide a unique set of estimates for the three unknown parameters in  .
.In the case of general linear regression, the above statement is equivalent to the requirement that the matrix
 is invertible.
is invertible.When the number of measurements,
 , is larger than the number of unknown parameters,
, is larger than the number of unknown parameters,  , and the measurement errors
, and the measurement errors  are normally distributed then the excess of information contained in
are normally distributed then the excess of information contained in  measurements is used to make statistical predictions about the unknown
parameters. This excess of information is referred to as the degrees of freedom of the regression.
measurements is used to make statistical predictions about the unknown
parameters. This excess of information is referred to as the degrees of freedom of the regression.Underlying assumptions
Classical assumptions for regression analysis include:- The sample is representative of the population for the inference prediction.
- The error is a random variable with a mean of zero conditional on the explanatory variables.
- The independent variables are measured with no error. (Note: If this is not so, modeling may be done instead using errors-in-variables model techniques).
- The independent variables (predictors) are linearly independent, i.e. it is not possible to express any predictor as a linear combination of the others.
- The errors are uncorrelated, that is, the variance–covariance matrix of the errors is diagonal and each non-zero element is the variance of the error.
- The variance of the error is constant across observations (homoscedasticity). If not, weighted least squares or other methods might instead be used.
Independent and dependent variables often refer to values measured at point locations. There may be spatial trends and spatial autocorrelation in the variables that violate statistical assumptions of regression. Geographic weighted regression is one technique to deal with such data.[20] Also, variables may include values aggregated by areas. With aggregated data the modifiable areal unit problem can cause extreme variation in regression parameters.[21] When analyzing data aggregated by political boundaries, postal codes or census areas results may be very distinct with a different choice of units.
Linear regression
In linear regression, the model specification is that the dependent variable, is a linear combination of the parameters (but need not be linear in the independent variables). For example, in simple linear regression for modeling
is a linear combination of the parameters (but need not be linear in the independent variables). For example, in simple linear regression for modeling  data points there is one independent variable:
data points there is one independent variable:  , and two parameters,
, and two parameters,  and
and  :
:
- straight line:
Adding a term in
 to the preceding regression gives:
to the preceding regression gives:- parabola:
 , it is linear in the parameters
, it is linear in the parameters  ,
,  and
and 
In both cases,
 is an error term and the subscript
is an error term and the subscript  indexes a particular observation.
indexes a particular observation.Returning our attention to the straight line case: Given a random sample from the population, we estimate the population parameters and obtain the sample linear regression model:
 , is the difference between the value of the dependent variable predicted by the model,
, is the difference between the value of the dependent variable predicted by the model,  , and the true value of the dependent variable,
, and the true value of the dependent variable,  . One method of estimation is ordinary least squares. This method obtains parameter estimates that minimize the sum of squared residuals, SSR:
. One method of estimation is ordinary least squares. This method obtains parameter estimates that minimize the sum of squared residuals, SSR: .
.
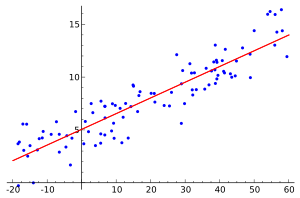
Illustration of linear regression on a data set.
In the case of simple regression, the formulas for the least squares estimates are
 is the mean (average) of the
is the mean (average) of the  values and
values and  is the mean of the
is the mean of the  values.
values.Under the assumption that the population error term has a constant variance, the estimate of that variance is given by:
 for
for  regressors or
regressors or  if an intercept is used.[22] In this case,
if an intercept is used.[22] In this case,  so the denominator is
so the denominator is  .
.The standard errors of the parameter estimates are given by
.
General linear model
In the more general multiple regression model, there are independent variables:
independent variables:
 is the
is the  -th observation on the
-th observation on the  -th independent variable. If the first independent variable takes the value 1 for all
-th independent variable. If the first independent variable takes the value 1 for all  ,
,  , then
, then  is called the regression intercept.
is called the regression intercept.The least squares parameter estimates are obtained from
 normal equations. The residual can be written as
normal equations. The residual can be written as element of
element of  is
is  , the
, the  element of the column vector
element of the column vector  is
is  , and the
, and the  element of
element of  is
is  . Thus
. Thus  is
is  ,
,  is
is  , and
, and  is
is  . The solution is
. The solution isDiagnostics
Once a regression model has been constructed, it may be important to confirm the goodness of fit of the model and the statistical significance of the estimated parameters. Commonly used checks of goodness of fit include the R-squared, analyses of the pattern of residuals and hypothesis testing. Statistical significance can be checked by an F-test of the overall fit, followed by t-tests of individual parameters.Interpretations of these diagnostic tests rest heavily on the model assumptions. Although examination of the residuals can be used to invalidate a model, the results of a t-test or F-test are sometimes more difficult to interpret if the model's assumptions are violated. For example, if the error term does not have a normal distribution, in small samples the estimated parameters will not follow normal distributions and complicate inference. With relatively large samples, however, a central limit theorem can be invoked such that hypothesis testing may proceed using asymptotic approximations.
Limited dependent variables
Limited dependent variables, which are response variables that are categorical variables or are variables constrained to fall only in a certain range, often arise in econometrics.The response variable may be non-continuous ("limited" to lie on some subset of the real line). For binary (zero or one) variables, if analysis proceeds with least-squares linear regression, the model is called the linear probability model. Nonlinear models for binary dependent variables include the probit and logit model. The multivariate probit model is a standard method of estimating a joint relationship between several binary dependent variables and some independent variables. For categorical variables with more than two values there is the multinomial logit. For ordinal variables with more than two values, there are the ordered logit and ordered probit models. Censored regression models may be used when the dependent variable is only sometimes observed, and Heckman correction type models may be used when the sample is not randomly selected from the population of interest. An alternative to such procedures is linear regression based on polychoric correlation (or polyserial correlations) between the categorical variables. Such procedures differ in the assumptions made about the distribution of the variables in the population. If the variable is positive with low values and represents the repetition of the occurrence of an event, then count models like the Poisson regression or the negative binomial model may be used
Interpolation and extrapolation
In the middle, the interpolated straight line represents the best
balance between the points above and below this line. The dotted lines
represent the two extreme lines. The first curves represent the
estimated values. The outer curves represent a prediction for a new
measurement[23].
Regression models predict a value of the Y variable given known values of the X variables. Prediction within the range of values in the dataset used for model-fitting is known informally as interpolation. Prediction outside this range of the data is known as extrapolation. Performing extrapolation relies strongly on the regression assumptions. The further the extrapolation goes outside the data, the more room there is for the model to fail due to differences between the assumptions and the sample data or the true values.
It is generally advised[citation needed] that when performing extrapolation, one should accompany the estimated value of the dependent variable with a prediction interval that represents the uncertainty. Such intervals tend to expand rapidly as the values of the independent variable(s) moved outside the range covered by the observed data.
For such reasons and others, some tend to say that it might be unwise to undertake extrapolation.[24]
However, this does not cover the full set of modeling errors that may be made: in particular, the assumption of a particular form for the relation between Y and X. A properly conducted regression analysis will include an assessment of how well the assumed form is matched by the observed data, but it can only do so within the range of values of the independent variables actually available. This means that any extrapolation is particularly reliant on the assumptions being made about the structural form of the regression relationship. Best-practice advice here[citation needed] is that a linear-in-variables and linear-in-parameters relationship should not be chosen simply for computational convenience, but that all available knowledge should be deployed in constructing a regression model. If this knowledge includes the fact that the dependent variable cannot go outside a certain range of values, this can be made use of in selecting the model – even if the observed dataset has no values particularly near such bounds. The implications of this step of choosing an appropriate functional form for the regression can be great when extrapolation is considered. At a minimum, it can ensure that any extrapolation arising from a fitted model is "realistic" (or in accord with what is known).
Nonlinear regression
When the model function is not linear in the parameters, the sum of squares must be minimized by an iterative procedure. This introduces many complications which are summarized in Differences between linear and non-linear least squares.Power and sample size calculations
There are no generally agreed methods for relating the number of observations versus the number of independent variables in the model. One rule of thumb suggested by Good and Hardin is , where
, where  is the sample size,
is the sample size,  is the number of independent variables and
is the number of independent variables and  is the number of observations needed to reach the desired precision if the model had only one independent variable.[25] For example, a researcher is building a linear regression model using a dataset that contains 1000 patients (
is the number of observations needed to reach the desired precision if the model had only one independent variable.[25] For example, a researcher is building a linear regression model using a dataset that contains 1000 patients ( ). If the researcher decides that five observations are needed to precisely define a straight line (
). If the researcher decides that five observations are needed to precisely define a straight line ( ), then the maximum number of independent variables the model can support is 4, because
), then the maximum number of independent variables the model can support is 4, because .
.Other methods
Although the parameters of a regression model are usually estimated using the method of least squares, other methods which have been used include:- Bayesian methods, e.g. Bayesian linear regression
- Percentage regression, for situations where reducing percentage errors is deemed more appropriate.[26]
- Least absolute deviations, which is more robust in the presence of outliers, leading to quantile regression
- Nonparametric regression, requires a large number of observations and is computationally intensive
- Distance metric learning, which is learned by the search of a meaningful distance metric in a given input space.[27]