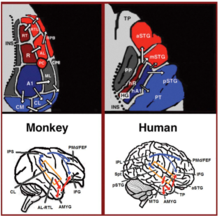
Dual stream connectivity between the auditory cortex and frontal lobe of monkeys and humans. Top: The auditory cortex of the monkey (left) and human (right) is schematically depicted on the supratemporal plane and observed from above (with the parieto- frontal operculi removed). Bottom: The brain of the monkey (left) and human (right) is schematically depicted and displayed from the side. Orange frames mark the region of the auditory cortex, which is displayed in the top sub-figures. Top and Bottom: Blue colors mark regions affiliated with the ADS, and red colors mark regions affiliated with the AVS (dark red and blue regions mark the primary auditory fields). Abbreviations: AMYG-amygdala, HG-Heschl’s gyrus, FEF-frontal eye field, IFG-inferior frontal gyrus, INS-insula, IPS-intra parietal sulcus, MTG-middle temporal gyrus, PC-pitch center, PMd-dorsal premotor cortex, PP-planum polare, PT-planum temporale, TP-temporal pole, Spt-sylvian parietal-temporal, pSTG/mSTG/aSTG-posterior/middle/anterior superior temporal gyrus, CL/ ML/AL/RTL-caudo-/middle-/antero-/rostrotemporal-lateral belt area, CPB/RPB-caudal/rostral parabelt fields.
Language processing refers to the way humans use words to communicate ideas and feelings, and how such communications are processed and understood. Language processing is considered to be an uniquely human ability that is not produced with the same grammatical understanding or systematicity in even human's closest primate relatives.
Throughout the 20th century the dominant model for language processing in the brain was the Geschwind-Lichteim-Wernicke model, which is based primarily on the analysis of brain damaged patients. However, due to improvements in intra-cortical electrophysiological recordings of monkey and human brains, as well non-invasive techniques such as fMRI, PET, MEG and EEG, a dual auditory pathway has been revealed. In accordance with this model, there are two pathways that connect the auditory cortex to the frontal lobe, each pathway accounting for different linguistic roles. The auditory ventral stream connects the auditory cortex with the middle temporal gyrus and temporal pole, which in turn connects with the inferior frontal gyrus. This pathway is responsible for sound recognition, and is accordingly known as the auditory 'what' pathway. The auditory dorsal stream connects the auditory cortex with the parietal lobe, which in turn connects with inferior frontal gyrus. In both humans and non-human primates, the auditory dorsal stream is responsible for sound localization, and is accordingly known as the auditory 'where' pathway. In humans, this pathway (especially in the left hemisphere) is also responsible for speech production, speech repetition, lip-reading, and phonological working memory and long-term memory. In accordance with the 'from where to what' model of language evolution. the reason the ADS is characterized with such a broad range of functions is that each indicates a different stage in language evolution.
History of neurolinguistics
Throughout the 20th century, our knowledge of language processing in the brain was dominated by the Wernicke-Lichtheim-Geschwind model. This model is primarily based on research conducted on brain-damaged individuals who were reported to possess a variety of language related disorders. In accordance with this model, words are perceived via a specialized word reception center (Wernicke’s area) that is located in the left temporoparietal junction. This region then projects to a word production center (Broca’s area) that is located in the left inferior frontal gyrus. Because almost all language input was thought to funnel via Wernicke’s area and all language output to funnel via Broca’s area, it became extremely difficult to identify the basic properties of each region. This lack of clear definition for the contribution of Wernicke’s and Broca’s regions to human language rendered it extremely difficult to identify their homologues in other primates. With the advent of the MRI and its application for lesion mappings, however, it was shown that this model is based on incorrect correlations between symptoms and lesions. The refutation of such an influential and dominant model opened the door to new models of language processing in the brain.Anatomy of the auditory ventral and dorsal streams
In the last two decades, significant advances occurred in our understanding of the neural processing of sounds in primates. Initially by recording of neural activity in the auditory cortices of monkeys and later elaborated via histological staining and fMRI scanning studies, 3 auditory fields were identified in the primary auditory cortex, and 9 associative auditory fields were shown to surround them (Figure 1 top left). Anatomical tracing and lesion studies further indicated of a separation between the anterior and posterior auditory fields, with the anterior primary auditory fields (areas R-RT) projecting to the anterior associative auditory fields (areas AL-RTL), and the posterior primary auditory field (area A1) projecting to the posterior associative auditory fields (areas CL-CM). Recently, evidence accumulated that indicates homology between the human and monkey auditory fields. In humans, histological staining studies revealed two separate auditory fields in the primary auditory region of Heschl’s gyrus, and by mapping the tonotopic organization of the human primary auditory fields with high resolution fMRI and comparing it to the tonotopic organization of the monkey primary auditory fields, homology was established between the human anterior primary auditory field and monkey area R (denoted in humans as area hR) and the human posterior primary auditory field and the monkey area A1 (denoted in humans as area hA1). Intra-cortical recordings from the human auditory cortex further demonstrated similar patterns of connectivity to the auditory cortex of the monkey. Recording from the surface of the auditory cortex (supra-temporal plane) reported that the anterior Heschl’s gyrus (area hR) projects primarily to the middle-anterior superior temporal gyrus (mSTG-aSTG) and the posterior Heschl’s gyrus (area hA1) projects primarily to the posterior superior temporal gyrus (pSTG) and the planum temporale (area PT; Figure 1 top right). Consistent with connections from area hR to the aSTG and hA1 to the pSTG is an fMRI study of a patient with impaired sound recognition (auditory agnosia), who was shown with reduced bilateral activation in areas hR and aSTG but with spared activation in the mSTG-pSTG. This connectivity pattern is also corroborated by a study that recorded activation from the lateral surface of the auditory cortex and reported of simultaneous non-overlapping activation clusters in the pSTG and mSTG-aSTG while listening to sounds.Downstream to the auditory cortex, anatomical tracing studies in monkeys delineated projections from the anterior associative auditory fields (areas AL-RTL) to ventral prefrontal and premotor cortices in the inferior frontal gyrus (IFG) and amygdala. Cortical recording and functional imaging studies in macaque monkeys further elaborated on this processing stream by showing that acoustic information flows from the anterior auditory cortex to the temporal pole (TP) and then to the IFG. This pathway is commonly referred to as the auditory ventral stream (AVS; Figure 1, bottom left-red arrows). In contrast to the anterior auditory fields, tracing studies reported that the posterior auditory fields (areas CL-CM) project primarily to dorsolateral prefrontal and premotor cortices (although some projections do terminate in the IFG. Cortical recordings and anatomical tracing studies in monkeys further provided evidence that this processing stream flows from the posterior auditory fields to the frontal lobe via a relay station in the intra-parietal sulcus (IPS). This pathway is commonly referred to as the auditory dorsal stream (ADS; Figure 1, bottom left-blue arrows). Comparing the white matter pathways involved in communication in humans and monkeys with diffusion tensor imaging techniques indicates of similar connections of the AVS and ADS in the two species (Monkey, Human). In humans, the pSTG was shown to project to the parietal lobe (sylvian parietal-temporal junction- inferior parietal lobule; Spt-IPL), and from there to dorsolateral prefrontal and premotor cortices (Figure 1, bottom right-blue arrows), and the aSTG was shown to project to the anterior temporal lobe (middle temporal gyrus-temporal pole; MTG-TP) and from there to the IFG (Figure 1 bottom right-red arrows).
Auditory ventral stream
Sound Recognition
Accumulative converging evidence indicates that the AVS is involved in recognizing auditory objects. At the level of the primary auditory cortex, recordings from monkeys showed higher percentage of neurons selective for learned melodic sequences in area R than area A1, and a study in humans demonstrated more selectivity for heard syllables in the anterior Heschl’s gyrus (area hR) than posterior Heshcl’s gyrus (area hA1). In downstream associative auditory fields, studies from both monkeys and humans reported that the border between the anterior and posterior auditory fields (Figure 1-area PC in the monkey and mSTG in the human) processes pitch attributes that are necessary for the recognition of auditory objects. The anterior auditory fields of monkeys were also demonstrated with selectivity for con-specific vocalizations with intra-cortical recordings and functional imaging One fMRI monkey study further demonstrated a role of the aSTG in the recognition of individual voices. The role of the human mSTG-aSTG in sound recognition was demonstrated via functional imaging studies that correlated activity in this region with isolation of auditory objects from background noise, and with the recognition of spoken words, voices, melodies, environmental sounds, and non-speech communicative sounds. A Meta-analysis of fMRI studies further demonstrated functional dissociation between the left mSTG and aSTG, with the former processing short speech units (phonemes) and the latter processing longer units (e.g., words, environmental sounds). A study that recorded neural activity directly from the left pSTG and aSTG reported that the aSTG, but not pSTG, was more active when the patient listened to speech in her native language than unfamiliar foreign language. Consistently, electro stimulation to the aSTG of this patient resulted in impaired speech perception. Intra-cortical recordings from the right and left aSTG further demonstrated that speech is processed laterally to music. An fMRI study of a patient with impaired sound recognition (auditory agnosia) due to brainstem damage was also shown with reduced activation in areas hR and aSTG of both hemispheres when hearing spoken words and environmental sounds. Recordings from the anterior auditory cortex of monkeys while maintaining learned sounds in working memory, and the debilitating effect of induced lesions to this region on working memory recall, further implicate the AVS in maintaining the perceived auditory objects in working memory. In humans, area mSTG-aSTG was also reported active during rehearsal of heard syllables with MEG and fMRI. The latter study further demonstrated that working memory in the AVS is for the acoustic properties of spoken words and that it is independent to working memory in the ADS, which mediates inner speech. Working memory studies in monkeys also suggest that in monkeys, in contrast to humans, the AVS is the dominant working memory store.In humans, downstream to the aSTG, the MTG and TP are thought to constitute the semantic lexicon, which is a long-term memory repository of audio-visual representations that are interconnected on the basis of semantic relationships. The primary evidence for this role of the MTG-TP is that patients with damage to this region (e.g., patients with semantic dementia or herpes simplex virus encephalitis) are reported with an impaired ability to describe visual and auditory objects and a tendency to commit semantic errors when naming objects (i.e., semantic paraphasia). Semantic paraphasias were also expressed by aphasic patients with left MTG-TP damage and were shown to occur in non-aphasic patients after electro-stimulation to this region or the underlying white matter pathway. Two meta-analyses of the fMRI literature also reported that the anterior MTG and TP were consistently active during semantic analysis of speech and text; and an intra-cortical recording study correlated neural discharge in the MTG with the comprehension of intelligible sentences.
Sentence comprehension
In addition to extracting meaning from sounds, the MTG-TP region of the AVS appears to have a role in sentence comprehension, possibly by merging concepts together (e.g., merging the concept 'blue' and 'shirt to create the concept of a 'blue shirt'). The role of the MTG in extracting meaning from sentences has been demonstrated in functional imaging studies reporting stronger activation in the anterior MTG when proper sentences are contrasted with lists of words, sentences in a foreign or nonsense language, scrambled sentences, sentences with semantic or syntactic violations and sentence-like sequences of environmental sounds. One fMRI study in which participants were instructed to read a story further correlated activity in the anterior MTG with the amount of semantic and syntactic content each sentence contained. An EEG study that contrasted cortical activity while reading sentences with and without syntactic violations in healthy participants and patients with MTG-TP damage, concluded that the MTG-TP in both hemispheres participate in the automatic (rule based) stage of syntactic analysis (ELAN component), and that the left MTG-TP is also involved in a later controlled stage of syntax analysis (P600 component). Patients with damage to the MTG-TP region have also been reported with impaired sentence comprehension.Bilaterality
In contradiction to the Wernicke-Lichtheim-Geschwind model that implicates sound recognition to occur solely in the left hemisphere, studies that examined the properties of the right or left hemisphere in isolation via unilateral hemispheric anesthesia (i.e., the WADA procedure) or intra-cortical recordings from each hemisphere provided evidence that sound recognition is processed bilaterally. Moreover, a study that instructed patients with disconnected hemispheres (i.e., split-brain patients) to match spoken words to written words presented to the right or left hemifields, reported vocabulary in the right hemisphere that almost matches in size with the left hemisphere (the right hemisphere vocabulary was equivalent to the vocabulary of a healthy 11-years old child). This bilateral recognition of sounds is also consistent with the finding that unilateral lesion to the auditory cortex rarely results in deficit to auditory comprehension (i.e., auditory agnosia), whereas a second lesion to the remaining hemisphere (which could occur years later) does. Finally, as mentioned earlier, an fMRI scan of an auditory agnosia patient demonstrated bilateral reduced activation in the anterior auditory cortices, and bilateral electro-stimulation to these regions in both hemispheres resulted with impaired speech recognition.Auditory dorsal stream
Sound localization
The most established role of the ADS is with audiospatial processing. This is evidenced via studies that recorded neural activity from the auditory cortex of monkeys, and correlated the strongest selectivity to changes in sound location with the posterior auditory fields (areas CM-CL), intermediate selectivity with primary area A1, and very weak selectivity with the anterior auditory fields. In humans, behavioral studies of brain damaged patients and EEG recordings from healthy participants demonstrated that sound localization is processed independently of sound recognition, and thus is likely independent of processing in the AVS. Consistently, a working memory study reported two independent working memory storage spaces, one for acoustic properties and one for locations. Functional imaging studies that contrasted sound discrimination and sound localization reported a correlation between sound discrimination and activation in the mSTG-aSTG, and correlation between sound localization and activation in the pSTG and PT, with some studies further reporting of activation in the Spt-IPL region and frontal lobe. Some fMRI studies also reported that the activation in the pSTG and Spt-IPL regions increased when individuals perceived sounds in motion. EEG studies using source-localization also identified the pSTG-Spt region of the ADS as the sound localization processing center. A combined fMRI and MEG study corroborated the role of the ADS with audiospatial processing by demonstrating that changes in sound location resulted in activation spreading from Heschl’s gyrus posteriorly along the pSTG and terminating in the IPL. In another MEG study, the IPL and frontal lobe were shown active during maintenance of sound locations in working memory.Guidance of eye movements
In addition to localizing sounds, the ADS appears also to encode the sound location in memory, and to use this information for guiding eye movements. Evidence for the role of the ADS in encoding sounds into working memory is provided via studies that trained monkeys in a delayed matching to sample task, and reported of activation in areas CM-CL and IPS during the delay phase. Influence of this spatial information on eye movements occurs via projections of the ADS into the frontal eye field (FEF; a premotor area that is responsible for guiding eye movements) located in the frontal lobe. This is demonstrated with anatomical tracing studies that reported of connections between areas CM-CL-IPS and the FEF, and electro-physiological recordings that reported neural activity in both the IPS and the FEF prior to conducting saccadic eye-movements toward auditory targets.Integration of locations with auditory objects
A surprising function of the ADS is with the discrimination and possible identification of sounds, which is commonly ascribed with the anterior STG and STS of the AVS. However, electrophysiological recordings from the posterior auditory cortex (areas CM-CL), and IPS of monkeys, as well a PET monkey study reported of neurons that are selective to monkey vocalizations. One of these studies also reported of neurons in areas CM-CL that are characterized with dual selectivity for both a vocalization and a sound location. A monkey study that recorded electrophysiological activity from neurons in the posterior insula also reported of neurons that discriminate monkey calls based on the identity of the speaker. Similarly, human fMRI studies that instructed participants to discriminate voices reported an activation cluster in the pSTG. A study that recorded activity from the auditory cortex of an epileptic patient further reported that the pSTG, but not aSTG, was selective for the presence of a new speaker. A study that scanned fetuses in their third trimester of pregnancy with fMRI further reported of activation in area Spt when the hearing of voices was contrasted to pure tones. The researchers also reported that a sub-region of area Spt was more selective to their mother’s voice than unfamiliar female voices. This study thus suggests that the ADS is capable of identifying voices in addition to discriminating them.The manner in which sound recognition in the pSTG-PT-Spt regions of the ADS differs from sound recognition in the anterior STG and STS of the AVS was shown via electro-stimulation of an epileptic patient. This study reported that electro-stimulation of the aSTG resulted in changes in the perceived pitch of voices (including the patient’s own voice), whereas electro-stimulation of the pSTG resulted in reports that her voice was “drifting away.” This report indicates a role for the pSTG in the integration of sound location with an individual voice. Consistent with this role of the ADS is a study that reported patients, with AVS damage but spared ADS (surgical removal of the anterior STG/MTG), were no longer capable of isolating environmental sounds in the contralesional space, whereas their ability of isolating and discriminating human voices remained intact. Supporting a role for the pSTG-PT-Spt of the ADS with integrating auditory objects with sound locations are also studies that demonstrate a role for this region in the isolation of specific sounds. For example, two functional imaging studies correlated circumscribed pSTG-PT activation with the spreading of sounds into an increasing number of locations. Accordingly, an fMRI study correlated the perception of acoustic cues that are necessary for separating musical sounds (pitch chroma) with pSTG-PT activation.
Integration of phonemes with lip-movements
Although sound perception is primarily ascribed with the AVS, the ADS appears associated with several aspects of speech perception. For instance, in a meta-analysis of fMRI studies in which the auditory perception of phonemes was contrasted with closely matching sounds, and the studies were rated for the required level of attention, the authors concluded that attention to phonemes correlates with strong activation in the pSTG-pSTS region. An intra-cortical recording study in which participants were instructed to identify syllables also correlated the hearing of each syllable with its own activation pattern in the pSTG. Consistent with the role of the ADS in discriminating phonemes, studies have ascribed the integration of phonemes and their corresponding lip movements (i.e., visemes) to the pSTS of the ADS. For example, an fMRI study has correlated activation in the pSTS with the McGurk illusion (in which hearing the syllable “ba” while seeing the viseme “ga” results in the perception of the syllable “da”). Another study has found that using magnetic stimulation to interfere with processing in this area further disrupts the McGurk illusion. The association of the pSTS with the audio-visual integration of speech has also been demonstrated in a study that presented participants with pictures of faces and spoken words of varying quality. The study reported that the pSTS selects for the combined increase of the clarity of faces and spoken words. Corroborating evidence has been provided by an fMRI study that contrasted the perception of audio-visual speech with audio-visual non-speech (pictures and sounds of tools). This study reported the detection of speech-selective compartments in the pSTS. In addition, an fMRI study that contrasted congruent audio-visual speech with incongruent speech (pictures of still faces) reported pSTS activation.Phonological long-term memory
A growing body of evidence indicates that humans, in addition to having a long-term store for word meanings located in the MTG-TP of the AVS (i.e., the semantic lexicon), also have a long-term store for the names of objects located in the Spt-IPL region of the ADS (i.e., the phonological lexicon). For example, a study examining patients with damage to the AVS (MTG damage) or damage to the ADS (IPL damage) reported that MTG damage results in individuals incorrectly identifying objects (e.g., calling a “goat” a “sheep,” an example of semantic paraphasia). Conversely, IPL damage results in individuals correctly identifying the object but incorrectly pronouncing its name (e.g., saying “gof” instead of “goat,” an example of phonemic paraphasia). Semantic paraphasia errors have also been reported in patients receiving intra-cortical electrical stimulation of the AVS (MTG), and phonemic paraphasia errors have been reported in patients whose ADS (pSTG, Spt, and IPL) received intra-cortical electrical stimulation. Further supporting the role of the ADS in object naming is an MEG study that localized activity in the IPL during the learning and during the recall of object names. A study that induced magnetic interference in participants’ IPL while they answered questions about an object reported that the participants were capable of answering questions regarding the object’s characteristics or perceptual attributes but were impaired when asked whether the word contained two or three syllables. An MEG study has also correlated recovery from anomia (a disorder characterized by an impaired ability to name objects) with changes in IPL activation. Further supporting the role of the IPL in encoding the sounds of words are studies reporting that, compared to monolinguals, bilinguals have greater cortical density in the IPL but not the MTG. Because evidence shows that, in bilinguals, different phonological representations of the same word share the same semantic representation, this increase in density in the IPL verifies the existence of the phonological lexicon: the semantic lexicon of bilinguals is expected to be similar in size to the semantic lexicon of monolinguals, whereas their phonological lexicon should be twice the size. Consistent with this finding, cortical density in the IPL of monolinguals also correlates with vocabulary size. Notably, the functional dissociation of the AVS and ADS in object-naming tasks is supported by cumulative evidence from reading research showing that semantic errors are correlated with MTG impairment and phonemic errors with IPL impairment. Based on these associations, the semantic analysis of text has been linked to the inferior-temporal gyrus and MTG, and the phonological analysis of text has been linked to the pSTG-Spt- IPL.Phonological working memory
Working memory is often treated as the temporary activation of the representations stored in long-term memory that are used for speech (phonological representations). This sharing of resources between working memory and speech is evident by the finding that speaking during rehearsal results in a significant reduction in the number of items that can be recalled from working memory (articulatory suppression). The involvement of the phonological lexicon in working memory is also evidenced by the tendency of individuals to make more errors when recalling words from a recently learned list of phonologically similar words than from a list of phonologically dissimilar words (the phonological similarity effect). Studies have also found that speech errors committed during reading are remarkably similar to speech errors made during the recall of recently learned, phonologically similar words from working memory. Patients with IPL damage have also been observed to exhibit both speech production errors and impaired working memory. Finally, the view that verbal working memory is the result of temporarily activating phonological representations in the ADS is compatible with recent models describing working memory as the combination of maintaining representations in the mechanism of attention in parallel to temporarily activating representations in long-term memory. It has been argued that the role of the ADS in the rehearsal of lists of words is the reason this pathway is active during sentence comprehension For a review of the role of the ADS in working memory, see.
The
'from where to what' model of language evolution hypotheses 7 stages of
language evolution: 1. The origin of speech is the exchange of contact
calls between mothers and offspring used to relocate each other in cases
of separation. 2. Offspring of early Homo modified the contact calls
with intonations in order to emit two types of contact calls: contact
calls that signal low level of distress and contact calls that signal
high-level of distress. 3. The use of two types of contact calls enabled
the first question-answer conversation. In this scenario, the offspring
emits a low-level distress call to express a desire to interact with an
object, and the mother responds with a low-level distress call to
enable the interaction or high-level distress call to prohibit it. 4.
The use of intonations improved over time, and eventually, individuals
acquired sufficient vocal control to invent new words to objects. 5. At
first, offspring learned the calls from their parents by imitating their
lip-movements. 6. As the learning of calls improved, babies learned new
calls (i.e., phonemes) through lip imitation only during infancy. After
that period, the memory of phonemes lasted for a lifetime, and older
children became capable of learning new calls (through mimicry) without
observing their parents' lip-movements. 7. Individuals became capable of
rehearsing sequences of calls. This enabled the learning of words with
several syllables, which increased vocabulary size. Further developments
to the brain circuit responsible for rehearsing poly-syllabic words
resulted with individuals capable of rehearsing lists of words
(phonological working memory), which served as the platform for
communication with sentences.