| https://en.wikipedia.org/wiki/Gravity |
Gravity (from Latin gravitas 'weight'), or gravitation, is a natural phenomenon by which all things with mass or energy—including planets, stars, galaxies, and even light—are attracted to (or gravitate toward) one another. On Earth, gravity gives weight to physical objects, and the Moon's gravity causes the ocean tides. The gravitational attraction of the original gaseous matter present in the Universe caused it to begin coalescing and forming stars and caused the stars to group together into galaxies, so gravity is responsible for many of the large-scale structures in the Universe. Gravity has an infinite range, although its effects become weaker as objects get further away.
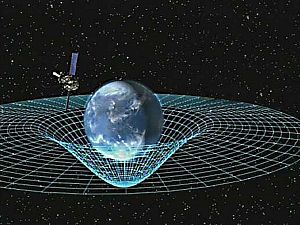
Gravity is most accurately described by the general theory of relativity (proposed by Albert Einstein in 1915), which describes gravity not as a force, but as a consequence of masses moving along geodesic lines in a curved spacetime caused by the uneven distribution of mass. The most extreme example of this curvature of spacetime is a black hole, from which nothing—not even light—can escape once past the black hole's event horizon. However, for most applications, gravity is well approximated by Newton's law of universal gravitation, which describes gravity as a force causing any two bodies to be attracted toward each other, with magnitude proportional to the product of their masses and inversely proportional to the square of the distance between them.
Gravity is the weakest of the four fundamental interactions of physics, approximately 1038 times weaker than the strong interaction, 1036 times weaker than the electromagnetic force and 1029 times weaker than the weak interaction. As a consequence, it has no significant influence at the level of subatomic particles. In contrast, it is the dominant interaction at the macroscopic scale, and is the cause of the formation, shape and trajectory (orbit) of astronomical bodies.
Current models of particle physics imply that the earliest instance of gravity in the Universe, possibly in the form of quantum gravity, supergravity or a gravitational singularity, along with ordinary space and time, developed during the Planck epoch (up to 10−43 seconds after the birth of the Universe), possibly from a primeval state, such as a false vacuum, quantum vacuum or virtual particle, in a currently unknown manner. Attempts to develop a theory of gravity consistent with quantum mechanics, a quantum gravity theory, which would allow gravity to be united in a common mathematical framework (a theory of everything) with the other three fundamental interactions of physics, are a current area of research.
History of gravitational theory
Ancient world
The ancient Greek philosopher Archimedes discovered the center of gravity of a triangle. He also postulated that if two equal weights did not have the same center of gravity, the center of gravity of the two weights together would be in the middle of the line that joins their centers of gravity.
The Roman architect and engineer Vitruvius in De Architectura postulated that gravity of an object did not depend on weight but its "nature".
Scientific revolution
Modern work on gravitational theory began with the work of Galileo Galilei in the late 16th and early 17th centuries. In his famous (though possibly apocryphal) experiment dropping balls from the Tower of Pisa, and later with careful measurements of balls rolling down inclines, Galileo showed that gravitational acceleration is the same for all objects. This was a major departure from Aristotle's belief that heavier objects have a higher gravitational acceleration. Galileo postulated air resistance as the reason that objects with low density and a high surface area fall more slowly in an atmosphere. Galileo's work set the stage for the formulation of Newton's theory of gravity.
Newton's theory of gravitation
In 1687, English mathematician Sir Isaac Newton published Principia, which hypothesizes the inverse-square law of universal gravitation. In his own words, "I deduced that the forces which keep the planets in their orbs must [be] reciprocally as the squares of their distances from the centers about which they revolve: and thereby compared the force requisite to keep the Moon in her Orb with the force of gravity at the surface of the Earth; and found them answer pretty nearly." The equation is the following:
Where F is the force, m1 and m2 are the masses of the objects interacting, r is the distance between the centers of the masses and G is the gravitational constant.
Newton's theory enjoyed its greatest success when it was used to predict the existence of Neptune based on motions of Uranus that could not be accounted for by the actions of the other planets. Calculations by both John Couch Adams and Urbain Le Verrier predicted the general position of the planet, and Le Verrier's calculations are what led Johann Gottfried Galle to the discovery of Neptune.
A discrepancy in Mercury's orbit pointed out flaws in Newton's theory. By the end of the 19th century, it was known that its orbit showed slight perturbations that could not be accounted for entirely under Newton's theory, but all searches for another perturbing body (such as a planet orbiting the Sun even closer than Mercury) had been fruitless. The issue was resolved in 1915 by Albert Einstein's new theory of general relativity, which accounted for the small discrepancy in Mercury's orbit. This discrepancy was the advance in the perihelion of Mercury of 42.98 arcseconds per century.
Although Newton's theory has been superseded by Albert Einstein's general relativity, most modern non-relativistic gravitational calculations are still made using Newton's theory because it is simpler to work with and it gives sufficiently accurate results for most applications involving sufficiently small masses, speeds and energies.
Equivalence principle
The equivalence principle, explored by a succession of researchers including Galileo, Loránd Eötvös, and Einstein, expresses the idea that all objects fall in the same way, and that the effects of gravity are indistinguishable from certain aspects of acceleration and deceleration. The simplest way to test the weak equivalence principle is to drop two objects of different masses or compositions in a vacuum and see whether they hit the ground at the same time. Such experiments demonstrate that all objects fall at the same rate when other forces (such as air resistance and electromagnetic effects) are negligible. More sophisticated tests use a torsion balance of a type invented by Eötvös. Satellite experiments, for example STEP, are planned for more accurate experiments in space.
Formulations of the equivalence principle include:
- The weak equivalence principle: The trajectory of a point mass in a gravitational field depends only on its initial position and velocity, and is independent of its composition.
- The Einsteinian equivalence principle: The outcome of any local non-gravitational experiment in a freely falling laboratory is independent of the velocity of the laboratory and its location in spacetime.
- The strong equivalence principle requiring both of the above.
General relativity
Einstein proposed that spacetime is curved by matter, and that free-falling objects are moving along locally straight paths in curved spacetime. These straight paths are called geodesics. Like Newton's first law of motion, Einstein's theory states that if a force is applied on an object, it would deviate from a geodesic. For instance, we are no longer following geodesics while standing because the mechanical resistance of the Earth exerts an upward force on us, and we are non-inertial on the ground as a result. This explains why moving along the geodesics in spacetime is considered inertial.
Einstein discovered the field equations of general relativity, which relate the presence of matter and the curvature of spacetime and are named after him. The Einstein field equations are a set of 10 simultaneous, non-linear, differential equations. The solutions of the field equations are the components of the metric tensor of spacetime. A metric tensor describes a geometry of spacetime. The geodesic paths for a spacetime are calculated from the metric tensor.
Solutions
Notable solutions of the Einstein field equations include:
- The Schwarzschild solution, which describes spacetime surrounding a spherically symmetric non-rotating uncharged massive object. For compact enough objects, this solution generated a black hole with a central singularity. For radial distances from the center which are much greater than the Schwarzschild radius, the accelerations predicted by the Schwarzschild solution are practically identical to those predicted by Newton's theory of gravity.
- The Reissner-Nordström solution, in which the central object has an electrical charge. For charges with a geometrized length which are less than the geometrized length of the mass of the object, this solution produces black holes with double event horizons.
- The Kerr solution for rotating massive objects. This solution also produces black holes with multiple event horizons.
- The Kerr-Newman solution for charged, rotating massive objects. This solution also produces black holes with multiple event horizons.
- The cosmological Friedmann-Lemaître-Robertson-Walker solution, which predicts the expansion of the Universe.
Tests
The tests of general relativity included the following:
- General relativity accounts for the anomalous perihelion precession of Mercury.
- The prediction that time runs slower at lower potentials (gravitational time dilation) has been confirmed by the Pound–Rebka experiment (1959), the Hafele–Keating experiment, and the GPS.
- The prediction of the deflection of light was first confirmed by Arthur Stanley Eddington from his observations during the Solar eclipse of 29 May 1919. Eddington measured starlight deflections twice those predicted by Newtonian corpuscular theory, in accordance with the predictions of general relativity. However, his interpretation of the results was later disputed. More recent tests using radio interferometric measurements of quasars passing behind the Sun have more accurately and consistently confirmed the deflection of light to the degree predicted by general relativity.
- The time delay of light passing close to a massive object was first identified by Irwin I. Shapiro in 1964 in interplanetary spacecraft signals.
- Gravitational radiation has been indirectly confirmed through studies of binary pulsars. On 11 February 2016, the LIGO and Virgo collaborations announced the first observation of a gravitational wave.
- Alexander Friedmann in 1922 found that Einstein equations have non-stationary solutions (even in the presence of the cosmological constant). In 1927 Georges Lemaître showed that static solutions of the Einstein equations, which are possible in the presence of the cosmological constant, are unstable, and therefore the static Universe envisioned by Einstein could not exist. Later, in 1931, Einstein himself agreed with the results of Friedmann and Lemaître. Thus general relativity predicted that the Universe had to be non-static—it had to either expand or contract. The expansion of the Universe discovered by Edwin Hubble in 1929 confirmed this prediction.
- The theory's prediction of frame dragging was consistent with the recent Gravity Probe B results.
- General relativity predicts that light should lose its energy when traveling away from massive bodies through gravitational redshift. This was verified on earth and in the solar system around 1960.
Gravity and quantum mechanics
An open question is whether it is possible to describe the small-scale interactions of gravity with the same framework as quantum mechanics. General relativity describes large-scale bulk properties whereas quantum mechanics is the framework to describe the smallest scale interactions of matter. Without modifications these frameworks are incompatible.
One path is to describe gravity in the framework of quantum field theory, which has been successful to accurately describe the other fundamental interactions. The electromagnetic force arises from an exchange of virtual photons, where the QFT description of gravity is that there is an exchange of virtual gravitons. This description reproduces general relativity in the classical limit. However, this approach fails at short distances of the order of the Planck length, where a more complete theory of quantum gravity (or a new approach to quantum mechanics) is required.
Specifics
Earth's gravity
Every planetary body (including the Earth) is surrounded by its own gravitational field, which can be conceptualized with Newtonian physics as exerting an attractive force on all objects. Assuming a spherically symmetrical planet, the strength of this field at any given point above the surface is proportional to the planetary body's mass and inversely proportional to the square of the distance from the center of the body.
The strength of the gravitational field is numerically equal to the acceleration of objects under its influence. The rate of acceleration of falling objects near the Earth's surface varies very slightly depending on latitude, surface features such as mountains and ridges, and perhaps unusually high or low sub-surface densities. For purposes of weights and measures, a standard gravity value is defined by the International Bureau of Weights and Measures, under the International System of Units (SI).
That value, denoted g, is g = 9.80665 m/s2 (32.1740 ft/s2).
The standard value of 9.80665 m/s2 is the one originally adopted by the International Committee on Weights and Measures in 1901 for 45° latitude, even though it has been shown to be too high by about five parts in ten thousand. This value has persisted in meteorology and in some standard atmospheres as the value for 45° latitude even though it applies more precisely to latitude of 45°32'33".
Assuming the standardized value for g and ignoring air resistance, this means that an object falling freely near the Earth's surface increases its velocity by 9.80665 m/s (32.1740 ft/s or 22 mph) for each second of its descent. Thus, an object starting from rest will attain a velocity of 9.80665 m/s (32.1740 ft/s) after one second, approximately 19.62 m/s (64.4 ft/s) after two seconds, and so on, adding 9.80665 m/s (32.1740 ft/s) to each resulting velocity. Also, again ignoring air resistance, any and all objects, when dropped from the same height, will hit the ground at the same time.
According to Newton's 3rd Law, the Earth itself experiences a force equal in magnitude and opposite in direction to that which it exerts on a falling object. This means that the Earth also accelerates towards the object until they collide. Because the mass of the Earth is huge, however, the acceleration imparted to the Earth by this opposite force is negligible in comparison to the object's. If the object does not bounce after it has collided with the Earth, each of them then exerts a repulsive contact force on the other which effectively balances the attractive force of gravity and prevents further acceleration.
The force of gravity on Earth is the resultant (vector sum) of two forces: (a) The gravitational attraction in accordance with Newton's universal law of gravitation, and (b) the centrifugal force, which results from the choice of an earthbound, rotating frame of reference. The force of gravity is weakest at the equator because of the centrifugal force caused by the Earth's rotation and because points on the equator are furthest from the center of the Earth. The force of gravity varies with latitude and increases from about 9.780 m/s2 at the Equator to about 9.832 m/s2 at the poles.
Equations for a falling body near the surface of the Earth
Under an assumption of constant gravitational attraction, Newton's law of universal gravitation simplifies to F = mg, where m is the mass of the body and g is a constant vector with an average magnitude of 9.81 m/s2 on Earth. This resulting force is the object's weight. The acceleration due to gravity is equal to this g. An initially stationary object which is allowed to fall freely under gravity drops a distance which is proportional to the square of the elapsed time. The image on the right, spanning half a second, was captured with a stroboscopic flash at 20 flashes per second. During the first 1⁄20 of a second the ball drops one unit of distance (here, a unit is about 12 mm); by 2⁄20 it has dropped at total of 4 units; by 3⁄20, 9 units and so on.
Under the same constant gravity assumptions, the potential energy, Ep, of a body at height h is given by Ep = mgh (or Ep = Wh, with W meaning weight). This expression is valid only over small distances h from the surface of the Earth. Similarly, the expression for the maximum height reached by a vertically projected body with initial velocity v is useful for small heights and small initial velocities only.
Gravity and astronomy
The application of Newton's law of gravity has enabled the acquisition of much of the detailed information we have about the planets in the Solar System, the mass of the Sun, and details of quasars; even the existence of dark matter is inferred using Newton's law of gravity. Although we have not traveled to all the planets nor to the Sun, we know their masses. These masses are obtained by applying the laws of gravity to the measured characteristics of the orbit. In space an object maintains its orbit because of the force of gravity acting upon it. Planets orbit stars, stars orbit galactic centers, galaxies orbit a center of mass in clusters, and clusters orbit in superclusters. The force of gravity exerted on one object by another is directly proportional to the product of those objects' masses and inversely proportional to the square of the distance between them.
The earliest gravity (possibly in the form of quantum gravity, supergravity or a gravitational singularity), along with ordinary space and time, developed during the Planck epoch (up to 10−43 seconds after the birth of the Universe), possibly from a primeval state (such as a false vacuum, quantum vacuum or virtual particle), in a currently unknown manner.
Gravitational radiation
General relativity predicts that energy can be transported out of a system through gravitational radiation. Any accelerating matter can create curvatures in the space-time metric, which is how the gravitational radiation is transported away from the system. Co-orbiting objects can generate curvatures in space-time such as the Earth-Sun system, pairs of neutron stars, and pairs of black holes. Another astrophysical system predicted to lose energy in the form of gravitational radiation are exploding supernovae.
The first indirect evidence for gravitational radiation was through measurements of the Hulse–Taylor binary in 1973. This system consists of a pulsar and neutron star in orbit around one another. Its orbital period has decreased since its initial discovery due to a loss of energy, which is consistent for the amount of energy loss due to gravitational radiation. This research was awarded the Nobel Prize in Physics in 1993.
The first direct evidence for gravitational radiation was measured on 14 September 2015 by the LIGO detectors. The gravitational waves emitted during the collision of two black holes 1.3 billion-light years from Earth were measured. This observation confirms the theoretical predictions of Einstein and others that such waves exist. It also opens the way for practical observation and understanding of the nature of gravity and events in the Universe including the Big Bang. Neutron star and black hole formation also create detectable amounts of gravitational radiation. This research was awarded the Nobel Prize in physics in 2017.
As of 2020, the gravitational radiation emitted by the Solar System is far too small to measure with current technology.
Speed of gravity
In December 2012, a research team in China announced that it had produced measurements of the phase lag of Earth tides during full and new moons which seem to prove that the speed of gravity is equal to the speed of light. This means that if the Sun suddenly disappeared, the Earth would keep orbiting the vacant point normally for 8 minutes, which is the time light takes to travel that distance. The team's findings were released in the Chinese Science Bulletin in February 2013.
In October 2017, the LIGO and Virgo detectors received gravitational wave signals within 2 seconds of gamma ray satellites and optical telescopes seeing signals from the same direction. This confirmed that the speed of gravitational waves was the same as the speed of light.
Anomalies and discrepancies
There are some observations that are not adequately accounted for, which may point to the need for better theories of gravity or perhaps be explained in other ways.

- Extra-fast stars: Stars in galaxies follow a distribution of velocities where stars on the outskirts are moving faster than they should according to the observed distributions of normal matter. Galaxies within galaxy clusters show a similar pattern. Dark matter, which would interact through gravitation but not electromagnetically, would account for the discrepancy. Various modifications to Newtonian dynamics have also been proposed.
- Flyby anomaly: Various spacecraft have experienced greater acceleration than expected during gravity assist maneuvers.
- Accelerating expansion: The metric expansion of space seems to be speeding up. Dark energy has been proposed to explain this. A recent alternative explanation is that the geometry of space is not homogeneous (due to clusters of galaxies) and that when the data are reinterpreted to take this into account, the expansion is not speeding up after all, however this conclusion is disputed.
- Anomalous increase of the astronomical unit: Recent measurements indicate that planetary orbits are widening faster than if this were solely through the Sun losing mass by radiating energy.
- Extra energetic photons: Photons travelling through galaxy clusters should gain energy and then lose it again on the way out. The accelerating expansion of the Universe should stop the photons returning all the energy, but even taking this into account photons from the cosmic microwave background radiation gain twice as much energy as expected. This may indicate that gravity falls off faster than inverse-squared at certain distance scales.
- Extra massive hydrogen clouds: The spectral lines of the Lyman-alpha forest suggest that hydrogen clouds are more clumped together at certain scales than expected and, like dark flow, may indicate that gravity falls off slower than inverse-squared at certain distance scales.