Solar cell efficiency refers to the portion of energy in the form of sunlight that can be converted via photovoltaics into electricity by the solar cell.
The efficiency of the solar cells used in a photovoltaic system, in combination with latitude and climate, determines the annual energy output of the system. For example, a solar panel with 20% efficiency and an area of 1 m2 will produce 200 kWh/yr at Standard Test Conditions if exposed to the Standard Test Condition solar irradiance value of 1000 W/m2 for 2.74 hours a day. Usually solar panels are exposed to sunlight for longer than this in a given day, but the solar irradiance is less than 1000 W/m2 for most of the day. A solar panel can produce more when the sun is high in the sky and will produce less in cloudy conditions or when the sun is low in the sky. The sun is lower in the sky in the winter. In a high yield solar area like central Colorado, which receives annual insolation of 2000 kWh/m2/year, such a panel can be expected to produce 400 kWh of energy per year. However, in Michigan, which receives only 1400 kWh/m2/year, annual energy yield will drop to 280 kWh for the same panel. At more northerly European latitudes, yields are significantly lower: 175 kWh annual energy yield in southern England under the same conditions.
Several factors affect a cell's conversion efficiency value, including its reflectance, thermodynamic efficiency, charge carrier separation efficiency, charge carrier collection efficiency and conduction efficiency values. Because these parameters can be difficult to measure directly, other parameters are measured instead, including quantum efficiency, open-circuit voltage (VOC) ratio, and § Fill factor (described below). Reflectance losses are accounted for by the quantum efficiency value, as they affect "external quantum efficiency." Recombination losses are accounted for by the quantum efficiency, VOC ratio, and fill factor values. Resistive losses are predominantly accounted for by the fill factor value, but also contribute to the quantum efficiency and VOC ratio values. In 2019, the world record for solar cell efficiency at 47.1% was achieved by using multi-junction concentrator solar cells, developed at National Renewable Energy Laboratory, Golden, Colorado, USA.
Factors affecting energy conversion efficiency
The factors affecting energy conversion efficiency were expounded in a landmark paper by William Shockley and Hans Queisser in 1961.
Thermodynamic efficiency limit and infinite-stack limit
If one has a source of heat at temperature Ts and cooler heat sink at temperature Tc, the maximum theoretically possible value for the ratio of work (or electric power) obtained to heat supplied is 1-Tc/Ts, given by a Carnot heat engine. If we take 6000 K for the temperature of the sun and 300 K for ambient conditions on earth, this comes to 95%. In 1981, Alexis de Vos and Herman Pauwels showed that this is achievable with a stack of an infinite number of cells with band gaps ranging from infinity (the first cells encountered by the incoming photons) to zero, with a voltage in each cell very close to the open-circuit voltage, equal to 95% of the band gap of that cell, and with 6000 K blackbody radiation coming from all directions. However, the 95% efficiency thereby achieved means that the electric power is 95% of the net amount of light absorbed – the stack emits radiation as it has non-zero temperature, and this radiation has to be subtracted from the incoming radiation when calculating the amount of heat being transferred and the efficiency. They also considered the more relevant problem of maximizing the power output for a stack being illuminated from all directions by 6000 K blackbody radiation. In this case, the voltages must be lowered to less than 95% of the band gap (the percentage is not constant over all the cells). The maximum theoretical efficiency calculated is 86.8% for a stack of an infinite number of cells, using the incoming concentrated sunlight radiation. When the incoming radiation comes only from an area of the sky the size of the sun, the efficiency limit drops to 68.7%.
Ultimate efficiency
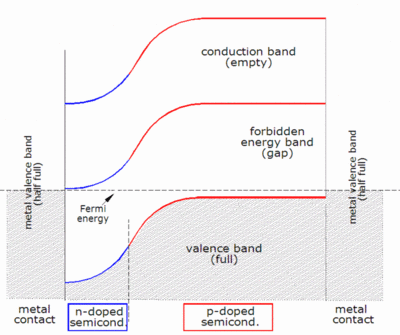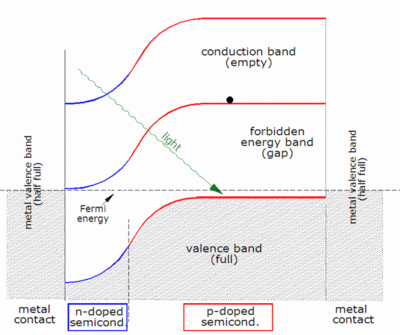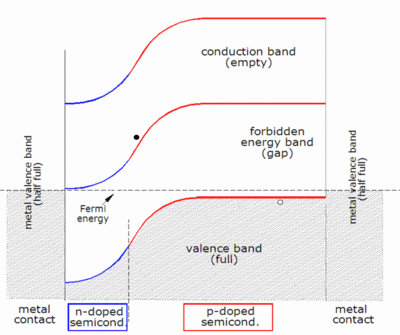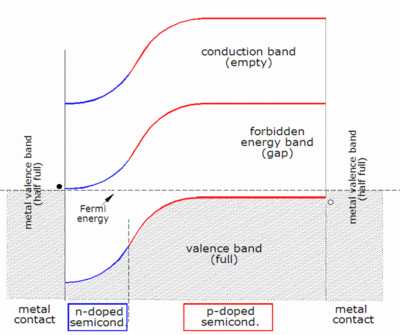
Normal photovoltaic systems however have only one p–n junction and are therefore subject to a lower efficiency limit, called the "ultimate efficiency" by Shockley and Queisser. Photons with an energy below the band gap of the absorber material cannot generate an electron-hole pair, so their energy is not converted to useful output, and only generates heat if absorbed. For photons with an energy above the band gap energy, only a fraction of the energy above the band gap can be converted to useful output. When a photon of greater energy is absorbed, the excess energy above the band gap is converted to kinetic energy of the carrier combination. The excess kinetic energy is converted to heat through phonon interactions as the kinetic energy of the carriers slows to equilibrium velocity. Traditional single-junction cells with an optimal band gap for the solar spectrum have a maximum theoretical efficiency of 33.16%, the Shockley–Queisser limit .
Solar cells with multiple band gap absorber materials improve efficiency by dividing the solar spectrum into smaller bins where the thermodynamic efficiency limit is higher for each bin.
Quantum efficiency
As described above, when a photon is absorbed by a solar cell it can produce an electron-hole pair. One of the carriers may reach the p–n junction and contribute to the current produced by the solar cell; such a carrier is said to be collected. Or, the carriers recombine with no net contribution to cell current.
Quantum efficiency refers to the percentage of photons that are converted to electric current (i.e., collected carriers) when the cell is operated under short circuit conditions. The "external" quantum efficiency of a silicon solar cell includes the effect of optical losses such as transmission and reflection.
In particular, some measures can be taken to reduce these losses. The reflection losses, which can account for up to 10% of the total incident energy, can be dramatically decreased using a technique called texturization, a light trapping method that modifies the average light path.
Quantum efficiency is most usefully expressed as a spectral measurement (that is, as a function of photon wavelength or energy). Since some wavelengths are absorbed more effectively than others, spectral measurements of quantum efficiency can yield valuable information about the quality of the semiconductor bulk and surfaces. Quantum efficiency alone is not the same as overall energy conversion efficiency, as it does not convey information about the fraction of power that is converted by the solar cell.
Maximum power point
A solar cell may operate over a wide range of voltages (V) and currents (I). By increasing the resistive load on an irradiated cell continuously from zero (a short circuit) to a very high value (an open circuit) one can determine the maximum power point, the point that maximizes V×I; that is, the load for which the cell can deliver maximum electrical power at that level of irradiation. (The output power is zero in both the short circuit and open circuit extremes).
The maximum power point of a solar cell is affected by its temperature. Knowing the technical data of certain solar cell, its power output at a certain temperature can be obtained by , where is the power generated at the standard testing condition; is the actual temperature of the solar cell.
A high quality, monocrystalline silicon solar cell, at 25 °C cell temperature, may produce 0.60 V open-circuit (VOC). The cell temperature in full sunlight, even with 25 °C air temperature, will probably be close to 45 °C, reducing the open-circuit voltage to 0.55 V per cell. The voltage drops modestly, with this type of cell, until the short-circuit current is approached (ISC). Maximum power (with 45 °C cell temperature) is typically produced with 75% to 80% of the open-circuit voltage (0.43 V in this case) and 90% of the short-circuit current. This output can be up to 70% of the VOC x ISC product. The short-circuit current (ISC) from a cell is nearly proportional to the illumination, while the open-circuit voltage (VOC) may drop only 10% with an 80% drop in illumination. Lower-quality cells have a more rapid drop in voltage with increasing current and could produce only 1/2 VOC at 1/2 ISC. The usable power output could thus drop from 70% of the VOC x ISC product to 50% or even as little as 25%. Vendors who rate their solar cell "power" only as VOC x ISC, without giving load curves, can be seriously distorting their actual performance.
The maximum power point of a photovoltaic varies with incident illumination. For example, accumulation of dust on photovoltaic panels reduces the maximum power point. For systems large enough to justify the extra expense, a maximum power point tracker tracks the instantaneous power by continually measuring the voltage and current (and hence, power transfer), and uses this information to dynamically adjust the load so the maximum power is always transferred, regardless of the variation in lighting.
Fill factor
Another defining term in the overall behavior of a solar cell is the fill factor (FF). This factor is a measure of quality of a solar cell. This is the available power at the maximum power point (Pm) divided by the open circuit voltage (VOC) and the short circuit current (ISC):
The fill factor can be represented graphically by the IV sweep, where it is the ratio of the different rectangular areas.
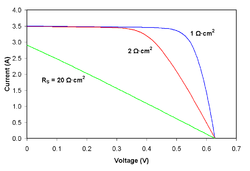
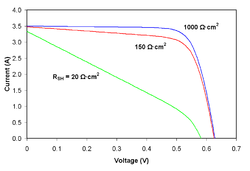
The fill factor is directly affected by the values of the cell's series, shunt resistances and diodes losses. Increasing the shunt resistance (Rsh) and decreasing the series resistance (Rs) lead to a higher fill factor, thus resulting in greater efficiency, and bringing the cell's output power closer to its theoretical maximum.
Typical fill factors range from 50% to 82%. The fill factor for a normal silicon PV cell is 80%.
Comparison
Energy conversion efficiency is measured by dividing the electrical output by the incident light power. Factors influencing output include spectral distribution, spatial distribution of power, temperature, and resistive load. IEC standard 61215 is used to compare the performance of cells and is designed around standard (terrestrial, temperate) temperature and conditions (STC): irradiance of 1 kW/m2, a spectral distribution close to solar radiation through AM (airmass) of 1.5 and a cell temperature 25 °C. The resistive load is varied until the peak or maximum power point (MPP) is achieved. The power at this point is recorded as Watt-peak (Wp). The same standard is used for measuring the power and efficiency of PV modules.
Air mass affects output. In space, where there is no atmosphere, the spectrum of the sun is relatively unfiltered. However, on earth, air filters the incoming light, changing the solar spectrum. The filtering effect ranges from Air Mass 0 (AM0) in space, to approximately Air Mass 1.5 on Earth. Multiplying the spectral differences by the quantum efficiency of the solar cell in question yields the efficiency. Terrestrial efficiencies typically are greater than space efficiencies. For example, a silicon solar cell in space might have an efficiency of 14% at AM0, but 16% on earth at AM 1.5. Note, however, that the number of incident photons in space is considerably larger, so the solar cell might produce considerably more power in space, despite the lower efficiency as indicated by reduced percentage of the total incident energy captured.
Solar cell efficiencies vary from 6% for amorphous silicon-based solar cells to 44.0% with multiple-junction production cells and 44.4% with multiple dies assembled into a hybrid package. Solar cell energy conversion efficiencies for commercially available multicrystalline Si solar cells are around 14–19%. The highest efficiency cells have not always been the most economical – for example a 30% efficient multijunction cell based on exotic materials such as gallium arsenide or indium selenide produced at low volume might well cost one hundred times as much as an 8% efficient amorphous silicon cell in mass production, while delivering only about four times the output.
However, there is a way to "boost" solar power. By increasing the light intensity, typically photogenerated carriers are increased, increasing efficiency by up to 15%. These so-called "concentrator systems" have only begun to become cost-competitive as a result of the development of high efficiency GaAs cells. The increase in intensity is typically accomplished by using concentrating optics. A typical concentrator system may use a light intensity 6–400 times the sun, and increase the efficiency of a one sun GaAs cell from 31% at AM 1.5 to 35%.
A common method used to express economic costs is to calculate a price per delivered kilowatt-hour (kWh). The solar cell efficiency in combination with the available irradiation has a major influence on the costs, but generally speaking the overall system efficiency is important. Commercially available solar cells (as of 2006) reached system efficiencies between 5 and 19%.
Undoped crystalline silicon devices are approaching the theoretical limiting efficiency of 29.43%. In 2017, efficiency of 26.63% was achieved in an amorphous silicon/crystalline silicon heterojunction cell that place both positive and negative contacts on the back of the cell.
Energy payback
The energy payback time is defined as the recovery time required for generating the energy spent for manufacturing a modern photovoltaic module. In 2008, it was estimated to be from 1 to 4 years depending on the module type and location. With a typical lifetime of 20 to 30 years, this means that modern solar cells would be net energy producers, i.e. they would generate more energy over their lifetime than the energy expended in producing them. Generally, thin-film technologies—despite having comparatively low conversion efficiencies—achieve significantly shorter energy payback times than conventional systems (often < 1 year).
A study published in 2013 which the existing literature found that energy payback time was between 0.75 and 3.5 years with thin film cells being at the lower end and multi-si-cells having a payback time of 1.5–2.6 years. A 2015 review assessed the energy payback time and EROI of solar photovoltaics. In this meta study, which uses an insolation of 1700 kWh/m2/year and a system lifetime of 30 years, mean harmonized EROIs between 8.7 and 34.2 were found. Mean harmonized energy payback time varied from 1.0 to 4.1 years. Crystalline silicon devices achieve on average an energy payback period of 2 years.
Like any other technology, solar cell manufacture is dependent on the existence of a complex global industrial manufacturing system. This includes the fabrication systems typically accounted for in estimates of manufacturing energy; the contingent mining, refining and global transportation systems; and other energy intensive support systems including finance, information, and security systems. The difficulty in measuring such energy overhead confers some uncertainty on any estimate of payback times.
Technical methods of improving efficiency
Choosing optimum transparent conductor
The illuminated side of some types of solar cells, thin films, have a transparent conducting film to allow light to enter into the active material and to collect the generated charge carriers. Typically, films with high transmittance and high electrical conductance such as indium tin oxide, conducting polymers or conducting nanowire networks are used for the purpose. There is a trade-off between high transmittance and electrical conductance, thus optimum density of conducting nanowires or conducting network structure should be chosen for high efficiency.
Promoting light scattering in the visible spectrum
Lining the light-receiving surface of the cell with nano-sized metallic studs can substantially increase the cell efficiency. Light reflects off these studs at an oblique angle to the cell, increasing the length of the light path through the cell. This increases the number of photons absorbed by the cell and the amount of current generated.
The main materials used for the nano-studs are silver, gold, and aluminium. Gold and silver are not very efficient, as they absorb much of the light in the visible spectrum, which contains most of the energy present in sunlight, reducing the amount of light reaching the cell. Aluminium absorbs only ultraviolet radiation, and reflects both visible and infra-red light, so energy loss is minimized. Aluminium can increase cell efficiency up to 22% (in lab conditions).
Radiative cooling
An increase in solar cell temperature of approximately 1 °C causes an efficiency decrease of about 0.45%. To prevent this, a transparent silica crystal layer can be applied to solar panels. The silica layer acts as a thermal black body which emits heat as infrared radiation into space, cooling the cell up to 13 °C.
Anti-reflective coatings and textures
Antireflective coatings could result in more destructive interference of incident light waves from the sun. Therefore, all sunlight would be transmitted into the photovoltaic. Texturizing, in which the surface of a solar cell is altered so that the reflected light strikes the surface again, is another technique used to reduce reflection. These surfaces can be created by etching or using lithography. Adding a flat back surface in addition to texturizing the front surface helps to trap the light within the cell, thus providing a longer optical path.
Rear surface passivation
Surface passivation is critical to solar cell efficiency. Many improvements have been made to the front side of mass-produced solar cells, but the aluminium back-surface is impeding efficiency improvements. The efficiency of many solar cells has benefitted by creating so-called passivated emitter and rear cells (PERCs). The chemical deposition of a rear-surface dielectric passivation layer stack that is also made of a thin silica or aluminium oxide film topped with a silicon nitride film helps to improve efficiency in silicon solar cells. This helped increase cell efficiency for commercial Cz-Si wafer material from just over 17% to over 21% by the mid-2010s, and the cell efficiency for quasi-mono-Si to a record 19.9%.
Concepts of the rear surface passivation for silicon solar cells has also been implemented for CIGS solar cells. The rear surface passivation shows the potential to improve the efficiency. Al2O3 and SiO2 have been used as the passivation materials. Nano-sized point contacts on Al2O3 layer and line contacts on SiO2 layer provide the electrical connection of CIGS absorber to the rear electrode Molybdenum. The point contacts on the Al2O3 layer are created by e-beam lithography and the line contacts on the SiO2 layer are created using photolithography. Also, the implementation of the passivation layers does not change the morphology of the CIGS layers.
Thin film materials
Thin film materials show a lot of promise for solar cells in terms of low costs and adaptability to existing structures and frameworks in technology. Since the materials are so thin, they lack the optical absorption of bulk material solar cells. Attempts to correct this have been tried, more important is thin film surface recombination. Since this is the dominant recombination process of nanoscale thin-film solar cells, it is crucial to their efficiency. Adding a passivating thin layer of silicon dioxide could reduce recombination.












![{\displaystyle I_{\text{D}}=I_{0}\left\{\exp \left[{\frac {V_{\text{j}}}{nV_{\text{T}}}}\right]-1\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbe8276fc9ce52e49f8cd1759d96c3db2896c448)



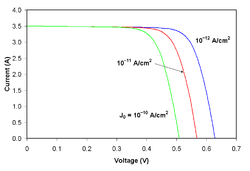
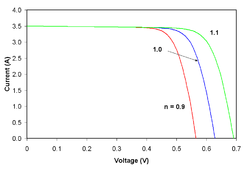
![{\displaystyle I=I_{\text{L}}-I_{0}\left\{\exp \left[{\frac {V+IR_{\text{S}}}{nV_{\text{T}}}}\right]-1\right\}-{\frac {V+IR_{\text{S}}}{R_{\text{SH}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5aa99f8a1a5cd6a0592ef6a1e4dbf538541a0236)







![{\displaystyle J=J_{\text{L}}-J_{0}\left\{\exp \left[{\frac {q(V+Jr_{\text{S}})}{nkT}}\right]-1\right\}-{\frac {V+Jr_{\text{S}}}{r_{\text{SH}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f4de764eaa5a2b639097a23218a8247712f32e1)