Proton decay

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Proton_decay 

The pattern of weak isospins, weak hypercharges, and color charges for particles in the Georgi–Glashow model. Here, a proton, consisting of two up quarks and a down, decays into a pion, consisting of an up and anti-up, and a positron, via an X boson with electric charge −⁴/₃.

In particle physics, proton decay is a hypothetical form of particle decay in which the proton decays into lighter subatomic particles, such as a neutral pion and a positron. The proton decay hypothesis was first formulated by Andrei Sakharov in 1967. Despite significant experimental effort, proton decay has never been observed. If it does decay via a positron, the proton's half-life is constrained to be at least 1.67×10³⁴ years.

According to the Standard Model, the proton, a type of baryon, is stable because baryon number (quark number) is conserved (under normal circumstances; see chiral anomaly for exception). Therefore, protons will not decay into other particles on their own, because they are the lightest (and therefore least energetic) baryon. Positron emission – a form of radioactive decay which sees a proton become a neutron – is not proton decay, since the proton interacts with other particles within the atom.

Some beyond-the-Standard Model grand unified theories (GUTs) explicitly break the baryon number symmetry, allowing protons to decay via the Higgs particle, magnetic monopoles, or new X bosons with a half-life of 10³¹ to 10³⁶ years. For comparison, the universe is roughly 10¹⁰ years old. To date, all attempts to observe new phenomena predicted by GUTs (like proton decay or the existence of magnetic monopoles) have failed.

Quantum tunnelling may be one of the mechanisms of proton decay.

Quantum gravity (via virtual black holes and Hawking radiation) may also provide a venue of proton decay at magnitudes or lifetimes well beyond the GUT scale decay range above, as well as extra dimensions in supersymmetry.

There are theoretical methods of baryon violation other than proton decay including interactions with changes of baryon and/or lepton number other than 1 (as required in proton decay). These included B and/or L violations of 2, 3, or other numbers, or B − L violation. Such examples include neutron oscillations and the electroweak sphaleron anomaly at high energies and temperatures that can result between the collision of protons into antileptons or vice versa (a key factor in leptogenesis and non-GUT baryogenesis).

Baryogenesis

Main article: Baryogenesis

Unsolved problem in physics:

Do protons decay? If so, then what is the half-life? Can nuclear binding energy affect this?

One of the outstanding problems in modern physics is the predominance of matter over antimatter in the universe. The universe, as a whole, seems to have a nonzero positive baryon number density – that is, matter exists. Since it is assumed in cosmology that the particles we see were created using the same physics we measure today, it would normally be expected that the overall baryon number should be zero, as matter and antimatter should have been created in equal amounts. This has led to a number of proposed mechanisms for symmetry breaking that favour the creation of normal matter (as opposed to antimatter) under certain conditions. This imbalance would have been exceptionally small, on the order of 1 in every 10000000000 (10¹⁰) particles a small fraction of a second after the Big Bang, but after most of the matter and antimatter annihilated, what was left over was all the baryonic matter in the current universe, along with a much greater number of bosons.

Most grand unified theories explicitly break the baryon number symmetry, which would account for this discrepancy, typically invoking reactions mediated by very massive X bosons (
X
) or massive Higgs bosons (
H⁰
). The rate at which these events occur is governed largely by the mass of the intermediate
X
or
H⁰
particles, so by assuming these reactions are responsible for the majority of the baryon number seen today, a maximum mass can be calculated above which the rate would be too slow to explain the presence of matter today. These estimates predict that a large volume of material will occasionally exhibit a spontaneous proton decay.

Experimental evidence

Proton decay is one of the key predictions of the various grand unified theories (GUTs) proposed in the 1970s, another major one being the existence of magnetic monopoles. Both concepts have been the focus of major experimental physics efforts since the early 1980s. To date, all attempts to observe these events have failed; however, these experiments have been able to establish lower bounds on the half-life of the proton. Currently the most precise results come from the Super-Kamiokande water Cherenkov radiation detector in Japan: a 2015 analysis placed a lower bound on the proton's half-life of 1.67×10³⁴ years via positron decay, and similarly, a 2012 analysis gave a lower bound to the proton's half-life of 1.08×10³⁴ years via antimuon decay, close to a supersymmetry (SUSY) prediction of 10³⁴–10³⁶ years. An upgraded version, Hyper-Kamiokande, probably will have sensitivity 5–10 times better than Super-Kamiokande.

Theoretical motivation

Despite the lack of observational evidence for proton decay, some grand unification theories, such as the SU(5) Georgi–Glashow model and SO(10), along with their supersymmetric variants, require it. According to such theories, the proton has a half-life of about 10³¹~10³⁶ years and decays into a positron and a neutral pion that itself immediately decays into two gamma ray photons:

p+	→	e+	+	π0
				└→	2 γ

Since a positron is an antilepton this decay preserves B - L number, which is conserved in most GUTs.

Additional decay modes are available (e.g.:
p⁺
→
μ⁺
+
π⁰
), both directly and when catalyzed via interaction with GUT-predicted magnetic monopoles. Though this process has not been observed experimentally, it is within the realm of experimental testability for future planned very large-scale detectors on the megaton scale. Such detectors include the Hyper-Kamiokande.

Early grand unification theories (GUTs) such as the Georgi–Glashow model, which were the first consistent theories to suggest proton decay, postulated that the proton's half-life would be at least 10³¹ years. As further experiments and calculations were performed in the 1990s, it became clear that the proton half-life could not lie below 10³² years. Many books from that period refer to this figure for the possible decay time for baryonic matter. More recent findings have pushed the minimum proton half-life to at least 10³⁴~10³⁵ years, ruling out the simpler GUTs (including minimal SU(5) / Georgi–Glashow) and most non-SUSY models. The maximum upper limit on proton lifetime (if unstable), is calculated at 6 × 10³⁹ years, a bound applicable to SUSY models, with a maximum for (minimal) non-SUSY GUTs at 1.4 × 10³⁶ years.

Although the phenomenon is referred to as "proton decay", the effect would also be seen in neutrons bound inside atomic nuclei. Free neutrons – those not inside an atomic nucleus – are already known to decay into protons (and an electron and an antineutrino) in a process called beta decay. Free neutrons have a half-life of 14+2⁄3 minutes (610.2±0.8 s) due to the weak interaction. Neutrons bound inside a nucleus have an immensely longer half-life – apparently as great as that of the proton.

Projected proton lifetimes

Theory class	Proton lifetime (years)	Ruled out experimentally?
Minimal SU(5) (Georgi–Glashow)	1030–1031	Yes
Minimal SUSY SU(5)	1028–1032	Yes
SUGRA SU(5)	1032–1034	Yes
SUSY SO(10)	1032–1035	Partially
SUSY SU(5) (MSSM)	~1034	Partially
SUSY SU(5) – 5 dimensions	1034–1035	Partially
Minimal (Basic) SO(10) – Non-SUSY	< ~1035 (maximum range)	No
SUSY SO(10) MSSM G(224)	2·1034	No
Flipped SU(5) (MSSM)	1035–1036	No

The lifetime of the proton in vanilla SU(5) can be naively estimated as ${\displaystyle \tau _{p}\sim {\frac {M_{X}^{4}}{m_{p}^{5}}}}$. Supersymmetric GUTs with reunification scales around µ ~ 2×10¹⁶ GeV/c² yield a lifetime of around 10³⁴ yr, roughly the current experimental lower bound.

Decay operators

Dimension-6 proton decay operators

The dimension-6 proton decay operators are ${\displaystyle {\frac {qqql}{\Lambda ^{2}}}}$, ${\displaystyle {\frac {d^{c}u^{c}u^{c}e^{c}}{\Lambda ^{2}}}}$, ${\displaystyle {\frac {{\overline {e^{c}}}{\overline {u^{c}}}qq}{\Lambda ^{2}}}}$ and ${\displaystyle {\frac {{\overline {d^{c}}}{\overline {u^{c}}}ql}{\Lambda ^{2}}}}$ where ${\displaystyle \Lambda }$ is the cutoff scale for the Standard Model. All of these operators violate both baryon number (B) and lepton number (L) conservation but not the combination B − L.

In GUT models, the exchange of an X or Y boson with the mass Λ_GUT can lead to the last two operators suppressed by ${\displaystyle {\frac {1}{\Lambda _{GUT}^{2}}}}$. The exchange of a triplet Higgs with mass ${\displaystyle M}$ can lead to all of the operators suppressed by ${\displaystyle {\frac {1}{M^{2}}}}$. See doublet–triplet splitting problem.

• Proton decay. These graphics refer to the X bosons and Higgs bosons.
• 

  Dimension-6 proton decay mediated by the
  X boson (3,2)
  _−5⁄6 in SU(5) GUT

• 

  Dimension-6 proton decay mediated by the
  X boson (3,2)
  _1⁄6 in flipped SU(5) GUT

• 

  Dimension-6 proton decay mediated by the
  triplet Higgs T (3,1)
  _−1⁄3 and the
  anti-triplet Higgs T (3,1)
  _1⁄3 in SU(5) GUT

Dimension-5 proton decay operators

In supersymmetric extensions (such as the MSSM), we can also have dimension-5 operators involving two fermions and two sfermions caused by the exchange of a tripletino of mass M. The sfermions will then exchange a gaugino or Higgsino or gravitino leaving two fermions. The overall Feynman diagram has a loop (and other complications due to strong interaction physics). This decay rate is suppressed by ${\displaystyle {\frac {1}{MM_{SUSY}}}}$ where M_SUSY is the mass scale of the superpartners.

Dimension-4 proton decay operators

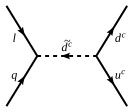
In the absence of matter parity, supersymmetric extensions of the Standard Model can give rise to the last operator suppressed by the inverse square of sdown quark mass. This is due to the dimension-4 operators
q

ℓ

d͂
^c and
u
^c
d
^c
d͂
^c.

The proton decay rate is only suppressed by ${\displaystyle {\frac {1}{M_{SUSY}^{2}}}}$ which is far too fast unless the couplings are very small.

Baryogenesis

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Baryogenesis 

 

Part of a series on
Physical cosmology
Big Bang · Universe Age of the universe Chronology of the universe

In physical cosmology, baryogenesis (also known as baryosynthesis) is the physical process that is hypothesized to have taken place during the early universe to produce baryonic asymmetry, i.e. the imbalance of matter (baryons) and antimatter (antibaryons) in the observed universe.

One of the outstanding problems in modern physics is the predominance of matter over antimatter in the universe. The universe, as a whole, seems to have a nonzero positive baryon number density. Since it is assumed in cosmology that the particles we see were created using the same physics we measure today, it would normally be expected that the overall baryon number should be zero, as matter and antimatter should have been created in equal amounts. A number of theoretical mechanisms are proposed to account for this discrepancy, namely identifying conditions that favour symmetry breaking and the creation of normal matter (as opposed to antimatter). This imbalance has to be exceptionally small, on the order of 1 in every 1630000000 (~2×10⁹) particles a small fraction of a second after the Big Bang. After most of the matter and antimatter was annihilated, what remained was all the baryonic matter in the current universe, along with a much greater number of bosons. Experiments reported in 2010 at Fermilab, however, seem to show that this imbalance is much greater than previously assumed. These experiments involved a series of particle collisions and found that the amount of generated matter was approximately 1% larger than the amount of generated antimatter. The reason for this discrepancy is not yet known.

Most grand unified theories explicitly break the baryon number symmetry, which would account for this discrepancy, typically invoking reactions mediated by very massive X bosons (
X
) or massive Higgs bosons (
H⁰
). The rate at which these events occur is governed largely by the mass of the intermediate
X
or
H⁰
particles, so by assuming these reactions are responsible for the majority of the baryon number seen today, a maximum mass can be calculated above which the rate would be too slow to explain the presence of matter today. These estimates predict that a large volume of material will occasionally exhibit a spontaneous proton decay, which has not been observed. Therefore, the imbalance between matter and antimatter remains a mystery.

Baryogenesis theories are based on different descriptions of the interaction between fundamental particles. Two main theories are electroweak baryogenesis (standard model), which would occur during the electroweak epoch, and the GUT baryogenesis, which would occur during or shortly after the grand unification epoch. Quantum field theory and statistical physics are used to describe such possible mechanisms.

Baryogenesis is followed by primordial nucleosynthesis, when atomic nuclei began to form.

Unsolved problem in physics:

Why does the observable universe have more matter than antimatter?

Background

The majority of ordinary matter in the universe is found in atomic nuclei, which are made of neutrons and protons. These nucleons are made up of smaller particles called quarks, and antimatter equivalents for each are predicted to exist by the Dirac equation in 1928. Since then, each kind of antiquark has been experimentally verified. Hypotheses investigating the first few instants of the universe predict a composition with an almost equal number of quarks and antiquarks. Once the universe expanded and cooled to a critical temperature of approximately 2×10¹² K, quarks combined into normal matter and antimatter and proceeded to annihilate up to the small initial asymmetry of about one part in five billion, leaving the matter around us. Free and separate individual quarks and antiquarks have never been observed in experiments—quarks and antiquarks are always found in groups of three (baryons), or bound in quark–antiquark pairs (mesons). Likewise, there is no experimental evidence that there are any significant concentrations of antimatter in the observable universe.

There are two main interpretations for this disparity: either the universe began with a small preference for matter (total baryonic number of the universe different from zero), or the universe was originally perfectly symmetric, but somehow a set of phenomena contributed to a small imbalance in favour of matter over time. The second point of view is preferred, although there is no clear experimental evidence indicating either of them to be the correct one.

GUT Baryogenesis under Sakharov conditions

In 1967, Andrei Sakharov proposed a set of three necessary conditions that a baryon-generating interaction must satisfy to produce matter and antimatter at different rates. These conditions were inspired by the recent discoveries of the cosmic background radiation and CP-violation in the neutral kaon system. The three necessary "Sakharov conditions" are:

• Baryon number ${\displaystyle B}$ violation.
• C-symmetry and CP-symmetry violation.
• Interactions out of thermal equilibrium.

Baryon number violation is a necessary condition to produce an excess of baryons over anti-baryons. But C-symmetry violation is also needed so that the interactions which produce more baryons than anti-baryons will not be counterbalanced by interactions which produce more anti-baryons than baryons. CP-symmetry violation is similarly required because otherwise equal numbers of left-handed baryons and right-handed anti-baryons would be produced, as well as equal numbers of left-handed anti-baryons and right-handed baryons. Finally, the interactions must be out of thermal equilibrium, since otherwise CPT symmetry would assure compensation between processes increasing and decreasing the baryon number.

Currently, there is no experimental evidence of particle interactions where the conservation of baryon number is broken perturbatively: this would appear to suggest that all observed particle reactions have equal baryon number before and after. Mathematically, the commutator of the baryon number quantum operator with the (perturbative) Standard Model hamiltonian is zero: ${\displaystyle [B,H]=BH-HB=0}$. However, the Standard Model is known to violate the conservation of baryon number only non-perturbatively: a global U(1) anomaly. To account for baryon violation in baryogenesis, such events (including proton decay) can occur in Grand Unification Theories (GUTs) and supersymmetric (SUSY) models via hypothetical massive bosons such as the X boson.

The second condition – violation of CP-symmetry – was discovered in 1964 (direct CP-violation, that is violation of CP-symmetry in a decay process, was discovered later, in 1999). Due to CPT symmetry, violation of CP-symmetry demands violation of time inversion symmetry, or T-symmetry.

In the out-of-equilibrium decay scenario, the last condition states that the rate of a reaction which generates baryon-asymmetry must be less than the rate of expansion of the universe. In this situation the particles and their corresponding antiparticles do not achieve thermal equilibrium due to rapid expansion decreasing the occurrence of pair-annihilation.

Baryogenesis within the Standard Model

The Standard Model can incorporate baryogenesis, though the amount of net baryons (and leptons) thus created may not be sufficient to account for the present baryon asymmetry. There is a required one excess quark per billion quark-antiquark pairs in the early universe in order to provide all the observed matter in the universe. This insufficiency has not yet been explained, theoretically or otherwise.

Baryogenesis within the Standard Model requires the electroweak symmetry breaking to be a first-order phase transition, since otherwise sphalerons wipe off any baryon asymmetry that happened up to the phase transition. Beyond this, the remaining amount of baryon non-conserving interactions is negligible.

The phase transition domain wall breaks the P-symmetry spontaneously, allowing for CP-symmetry violating interactions to break C-symmetry on both its sides. Quarks tend to accumulate on the broken phase side of the domain wall, while anti-quarks tend to accumulate on its unbroken phase side. Due to CP-symmetry violating electroweak interactions, some amplitudes involving quarks are not equal to the corresponding amplitudes involving anti-quarks, but rather have opposite phase (see CKM matrix and Kaon); since time reversal takes an amplitude to its complex conjugate, CPT-symmetry is conserved in this entire process.

Though some of their amplitudes have opposite phases, both quarks and anti-quarks have positive energy, and hence acquire the same phase as they move in space-time. This phase also depends on their mass, which is identical but depends both on flavor and on the Higgs VEV which changes along the domain wall. Thus certain sums of amplitudes for quarks have different absolute values compared to those of anti-quarks. In all, quarks and anti-quarks may have different reflection and transmission probabilities through the domain wall, and it turns out that more quarks coming from the unbroken phase are transmitted compared to anti-quarks.

Thus there is a net baryonic flux through the domain wall. Due to sphaleron transitions, which are abundant in the unbroken phase, the net anti-baryonic content of the unbroken phase is wiped off as anti-baryons are transformed into leptons. However, sphalerons are rare enough in the broken phase as not to wipe off the excess of baryons there. In total, there is net creation of baryons (as well as leptons).

In this scenario, non-perturbative electroweak interactions (i.e. the sphaleron) are responsible for the B-violation, the perturbative electroweak Lagrangian is responsible for the CP-violation, and the domain wall is responsible for the lack of thermal equilibrium and the P-violation; together with the CP-violation it also creates a C-violation in each of its sides.

Matter content in the universe

See also: Baryon asymmetry

The central question to Baryogenesis is what causes the preference for matter over antimatter in the universe, as well as the magnitude of this asymmetry. An important quantifier is the asymmetry parameter, given by

${\displaystyle \eta ={\frac {n_{B}-n_{\bar {B}}}{n_{\gamma }}}}$

where n_B and n_B refer to the number density of baryons and antibaryons respectively and n_γ is the number density of cosmic background radiation photons.

According to the Big Bang model, matter decoupled from the cosmic background radiation (CBR) at a temperature of roughly 3000 kelvin, corresponding to an average kinetic energy of 3000 K / (10.08×10³ K/eV) = 0.3 eV. After the decoupling, the total number of CBR photons remains constant. Therefore, due to space-time expansion, the photon density decreases. The photon density at equilibrium temperature T per cubic centimeter, is given by

${\displaystyle n_{\gamma }={\frac {1}{\pi ^{2}}}{\left({\frac {k_{B}T}{\hbar c}}\right)}^{3}\int _{0}^{\infty }{\frac {x^{2}}{e^{x}-1}}\operatorname {d} x={\frac {2\zeta (3)}{\pi ^{2}}}{\left({\frac {k_{B}T}{\hbar c}}\right)}^{3}\approx 20.3\left({\frac {T}{1{\text{K}}}}\right)^{3}{\text{cm}}^{-3}}$,

with k_B as the Boltzmann constant, ħ as the Planck constant divided by 2π and c as the speed of light in vacuum, and ζ(3) as Apéry's constant. At the current CBR photon temperature of 2.725 K, this corresponds to a photon density n_γ of around 411 CBR photons per cubic centimeter.

Therefore, the asymmetry parameter η, as defined above, is not the "best" parameter. Instead, the preferred asymmetry parameter uses the entropy density s,

${\displaystyle \eta _{s}={\frac {n_{B}-n_{\bar {B}}}{s}}}$

because the entropy density of the universe remained reasonably constant throughout most of its evolution. The entropy density is

${\displaystyle s\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathrm {entropy} }{\mathrm {volume} }}={\frac {p+\rho }{T}}={\frac {2\pi ^{2}}{45}}g_{\text{⁎}}(T)T^{3}}$

with p and ρ as the pressure and density from the energy density tensor T_μν, and g_⁎ as the effective number of degrees of freedom for "massless" particles at temperature T (in so far as mc² ≪ k_BT holds),

${\displaystyle g_{\text{⁎}}(T)=\sum _{\mathrm {i=bosons} }g_{i}{\left({\frac {T_{i}}{T}}\right)}^{3}+{\frac {7}{8}}\sum _{\mathrm {j=fermions} }g_{j}{\left({\frac {T_{j}}{T}}\right)}^{3}}$,

for bosons and fermions with g_i and g_j degrees of freedom at temperatures T_i and T_j respectively. At the present epoch, s = 7.04 n_γ.

Ongoing research efforts

Ties to dark matter

A possible explanation for the cause of baryogenesis is the decay reaction of B-Mesogenesis. This phenomena suggests that in the early universe, particles such as the B-meson decay into a visible Standard Model baryon as well as a dark antibaryon that is invisible to current observation techniques. The process begins by assuming a massive, long-lived, scalar particle ${\displaystyle \Phi }$ that exists in the early universe before Big Bang nucleosynthesis. The exact behavior of ${\displaystyle \Phi }$ is as yet unknown, but it is assumed to decay into b quarks and antiquarks in conditions outside of thermal equilibrium, thus satisfying one Sakharov condition. These b quarks form into B-mesons, which immediately hadronize into oscillating CP-violating ${\displaystyle B_{s}^{0}-{\bar {B}}_{s}^{0}}$ states, thus satisfying another Sakharov condition. These oscillating mesons then decay down into the baryon-dark antibaryon pair previously mentioned, ${\displaystyle B\rightarrow \psi {\mathcal {B}}{\mathcal {M}}}$, where ${\displaystyle B}$ is the parent B-meson, ${\displaystyle \psi }$ is the dark antibaryon, ${\displaystyle {\mathcal {B}}}$ is the visible baryon, and ${\displaystyle {\mathcal {M}}}$ is any extra light meson daughters required to satisfy other conservation laws in this particle decay. If this process occurs fast enough, the CP-violation effect gets carried over to the dark matter sector. However, this contradicts (or at least challenges) the last Sakharov condition, since the expected matter preference in the visible universe is balanced by a new antimatter preference in the dark matter of the universe and total baryon number is conserved.

B-Mesogenesis results in missing energy between the initial and final states of the decay process, which, if recorded, could provide experimental evidence for dark matter. Particle laboratories equipped with B-meson factories such as Belle and BaBar are extremely sensitive to B-meson decays involving missing energy and currently have the capability to detect the ${\displaystyle B\rightarrow \psi {\mathcal {B}}{\mathcal {M}}}$ channel. The LHC is also capable of searching for this interaction since it produces several orders of magnitude more B-mesons than Belle or BaBar, but there are more challenges from the decreased control over B-meson initial energy in the accelerator.

Missing baryon problem

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Missing_baryon_problem

In cosmology, the missing baryon problem is an observed discrepancy between the amount of baryonic matter detected from shortly after the Big Bang and from more recent epochs. Observations of the cosmic microwave background and Big Bang nucleosynthesis studies have set constraints on the abundance of baryons in the early universe, finding that baryonic matter accounts for approximately 4.8% of the energy contents of the Universe. At the same time, a census of baryons in the recent observable universe has found that observed baryonic matter accounts for less than half of that amount. This discrepancy is commonly known as the missing baryon problem. The missing baryon problem is different from the dark matter problem, which is non-baryonic in nature.

Early universe measurements

The abundance of baryonic matter in the early universe can be obtained indirectly from two independent methods:

• The theory of Big Bang nucleosynthesis, which predicts the observed relative abundance of the chemical elements in observations of the recent universe. Higher numbers of baryons in the early universe should produce higher ratios for helium, lithium, and heavier elements relative to hydrogen. Agreement with observed abundances requires that baryonic matter makes up between 4–5% of the universe's critical density.
• Detailed analysis of the small fluctuations (anisotropies) in the cosmic microwave background (CMB), especially the second peak of the CMB power spectrum. Baryonic matter interacts with photons and therefore leaves a visible imprint on the CMB. CMB analysis also yields a baryon fraction on the order of 5%.

The CMB constraint is much more precise than the BBN constraint, but the two are in agreement.

Late universe observations

The density of baryonic matter can be obtained directly by summing up all the known baryonic matter. This is highly nontrivial, since although luminous matter such as stars and galaxies are easily summed, baryonic matter can also exist in highly non-luminous form, such as black holes, planets, and highly diffuse interstellar gas. Nonetheless it can still be done, using a range of techniques:

• Making use of the Lyman-alpha forest; clouds of diffuse, baryonic gas or dust are sometimes visible when backlit by stars. The resulting spectra can be used to infer the mass between the star and the observer.
• Gravitational microlensing. If a planet or other dark object moves between the observer and a faraway source, the image of the source is distorted. The mass of the dark object can be inferred based on the amount of distortion.
• Sunyaev–Zel'dovich effect. The interaction between CMB photons and free electrons leaves an imprint in the CMB. This effect is sensitive to all free electrons independently of their temperature or the density of the surrounding medium, and thus it can be used to study baryonic matter otherwise not hot enough to be detected.

Generated image of the cosmic web which contains warm-hot regions where the missing baryons have been detected.

Prior to 2017, baryons were found to be distributed 10% inside galaxies, 50–60% in the circum-galactic medium, and 30–40% unaccounted, therefore accounting for about 70% of theoretical predictions.

Large scale galaxy surveys in the 2000s revealed a baryon deficit. This led theorists to reexamine their models and predict that gas must flow between galaxies and galaxy clusters.

Warm-Hot intergalactic medium

The Lambda-CDM model of the big bang predicts that matter between galaxies in the universe is distributed in web-like formations with a low density (1 - 10 particles per cubic meter) known as the Warm-hot intergalactic medium (WHIM). Cosmological hydrodynamical simulations from theory predict that a fraction of the missing baryons are located in the galactic halo at temperatures of 10⁶ K and the (WHIM) at temperatures of 10⁵–10⁷ K, with recent observations providing strong support. The WHIM is composed of three states:

• A warm state with temperatures 10⁵–10^5.7 K. Neutral hydrogen is present in this state. (Observed via Oxygen-VI absorption lines)
• A hot state with temperatures of 10^5.7–10^6.3 K. (Observed via Oxygen-VII in soft x-rays)
• A very hot state with temperatures of 10^6.3–10⁷ K. Very few hydrogen or hydrogen like metals, mostly present near the outskirts of galaxy clusters.

The warm phase of the WHIM had been previously detected and composes around 15% of the baryon content. The WHIM is mostly composed of ionized hydrogen. This creates difficulty for astronomers trying to detect baryons in the WHIM. It is easier to detect the WHIM through highly ionized oxygen such as OVI and OVII absorption.

Universe composition

The distribution of known baryons in the universe.

The census of known baryons in the universe tallied to around 60% of total baryons until the resolution of the missing baryon problem. This is in distinction from composition of the entire universe which includes dark energy and dark matter of which baryonic matter composes only 5%. Around 7% of baryons exists in stars and galaxies, while most of it exists around galaxies or galaxy clusters. The Lyman-alpha forest contains around 28% of the baryons. The warm phase of the WHIM was detected by soft X-ray absorption in 2012 to establish 15% of total baryon content. The intracluster medium (ICM) accounts for around 4% of total baryon content. It is composed of mostly ionized hydrogen and is about 10% of a galaxy cluster's total mass; the rest being dark matter. The ICM is low density with around 10⁻³ particles per cm³. The circum-galactic medium (CGM) was confirmed in 2003 by Chandra and Xmm-Newton. The CGM is a large sphere surrounding galaxies with a radius > 70 - 200 kpc. The CGM accounts for 5% of total baryons in the universe.

Detection methods

There are three main methods of detecting the WHIM where the missing baryons lie: the Sunyaev-Zel'dovich effect, Lyman-alpha emission lines, and metal absorption lines.

Sunyaev-Zel'dovich effect

The thermal Sunyaev-Zel'dovich (tSZ) effect occurs when photons from the CMB inverse Compton Scatter off ionized gas. For detecting baryons, the ionized gas from the WHIM is scattered by the CMB photons. The y-parameter quantifies the strength of the tSZ effect and is defined as:

${\displaystyle y=\int {\frac {k_{B}T_{e}}{m_{e}c^{2}}}n_{e}\sigma _{T}d\ell }$.

Where ${\displaystyle k_{b}}$ is Boltzmann's constant, ${\displaystyle \sigma _{T}}$ is the Thompson cross-section, ${\displaystyle n_{e}}$ is electron number density, ${\displaystyle m_{e}c^{2}}$ is the electron rest mass energy, and ${\displaystyle T_{e}}$ is the temperature. Finding the y-parameter and overlaying that with a map of cosmic filament from millions of galaxies allows astronomers to find the weak signal from the WHIM. The y-parameter signal from a galaxy pair is overlaid on a model for galaxy halos. The signals are subtracted to reveal a signal between the two galaxies. This resulting signal is the filament. To ensure the signal is not coming from any other source, astronomers generate a control simulation which they use to compare and are able to determine that source must be from the WHIM.

Lyman-Alpha emission

The Lyman-alpha (Lyα) emission lines are detected from ionized hydrogen in cosmic filament. A source, such as a quasar, ionizes hydrogen in the cosmic filament leaving detectable dips in the absorption lines.

Metal absorption lines

Highly ionized oxygen like O⁺⁶, O⁺⁷, and O⁺⁸ absorption lines in the soft X-rays at energies of 0.6 - 0.8 keV. The column density of these lines ${\displaystyle F(N_{O})}$ can be derived:

${\displaystyle \Omega _{O}={\frac {H_{0}m_{O}}{c\rho _{c}}}\int _{0}^{\infty }F(N_{O})N_{O}dN_{O}}$.

Where ${\displaystyle \Omega _{O}}$ is the abundance of a particular oxygen ion, ${\displaystyle H_{0}}$ is Hubble's constant, ${\displaystyle \rho _{c}}$ is the critical density ${\displaystyle \rho _{c}={\frac {3H^{2}}{8\pi G}}}$.

Claimed resolution

The missing baryon problem was proclaimed to be solved in 2017 when two groups of scientists who were working independently found evidence for the location of missing baryons in intergalactic matter. The missing baryons had been postulated to exist as hot strands between galaxy pairs (WHIM). Since the strands are diffuse and they are not hot enough to emit x-rays, they are difficult to detect. The groups used the thermal Sunyaev–Zeldovich effect to measure the density of the strands in the local Universe. If baryons are present there, then some amount of energy should be lost when light from the cosmic microwave background scatters off of them. These show up as very dim patches in the CMB. The patches are too dim to see directly, but when overlaid with the visible galaxy distribution, become detectable. The density of the strands comes up to about 30% of the baryonic density, the exact amount needed to solve the problem. Despite their success, these works only set constraints on the distribution of baryons between nearby galaxies, failing to provide a complete picture of cosmic gas in the late universe.

Using observations of the kinematic Sunyaev-Zel'dovich effect spanning more than 90% of the lifetime of the Universe, in 2021 astrophysicists found that approximately 50% of all baryonic matter is outside dark matter haloes, filling the space between galaxies. Together with the amount of baryons inside galaxies and surrounding these, the total amount of baryons in the late time Universe is now compatible with early Universe measurements.

Current state

Currently, many groups have observed the intergalactic medium and circum-galactic medium to obtain more measurements and observations of baryons to support the leading observations. Baryons have more or less been found, so groups are working to detect them to a higher level of significance. Methods used have included soft X-ray, OVI, OVII, and OVIII absorption.

In 2020 astrophysicists reported the first direct X-ray emissions measurement of baryonic matter of cosmic web filaments, strengthening empirical support for the recent solution to the problem.  The missing baryon problem has been resolved but research groups are working to detect the WHIM using varying methods to confirm results.