Expectation–maximization algorithm

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm 

In statistics, an expectation–maximization (EM) algorithm is an iterative method to find (local) maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step.

EM clustering of Old Faithful eruption data. The random initial model (which, due to the different scales of the axes, appears to be two very flat and wide spheres) is fit to the observed data. In the first iterations, the model changes substantially, but then converges to the two modes of the geyser. Visualized using ELKI.

History

The EM algorithm was explained and given its name in a classic 1977 paper by Arthur Dempster, Nan Laird, and Donald Rubin. They pointed out that the method had been "proposed many times in special circumstances" by earlier authors. One of the earliest is the gene-counting method for estimating allele frequencies by Cedric Smith. Another was proposed by H.O. Hartley in 1958, and Hartley and Hocking in 1977, from which many of the ideas in the Dempster-Laird-Rubin paper originated. Hartley’s ideas can be broadened to any grouped discrete distribution. A very detailed treatment of the EM method for exponential families was published by Rolf Sundberg in his thesis and several papers following his collaboration with Per Martin-Löf and Anders Martin-Löf. The Dempster–Laird–Rubin paper in 1977 generalized the method and sketched a convergence analysis for a wider class of problems. The Dempster–Laird–Rubin paper established the EM method as an important tool of statistical analysis.

The convergence analysis of the Dempster–Laird–Rubin algorithm was flawed and a correct convergence analysis was published by C. F. Jeff Wu in 1983. Wu's proof established the EM method's convergence outside of the exponential family, as claimed by Dempster–Laird–Rubin.

Introduction

The EM algorithm is used to find (local) maximum likelihood parameters of a statistical model in cases where the equations cannot be solved directly. Typically these models involve latent variables in addition to unknown parameters and known data observations. That is, either missing values exist among the data, or the model can be formulated more simply by assuming the existence of further unobserved data points. For example, a mixture model can be described more simply by assuming that each observed data point has a corresponding unobserved data point, or latent variable, specifying the mixture component to which each data point belongs.

Finding a maximum likelihood solution typically requires taking the derivatives of the likelihood function with respect to all the unknown values, the parameters and the latent variables, and simultaneously solving the resulting equations. In statistical models with latent variables, this is usually impossible. Instead, the result is typically a set of interlocking equations in which the solution to the parameters requires the values of the latent variables and vice versa, but substituting one set of equations into the other produces an unsolvable equation.

The EM algorithm proceeds from the observation that there is a way to solve these two sets of equations numerically. One can simply pick arbitrary values for one of the two sets of unknowns, use them to estimate the second set, then use these new values to find a better estimate of the first set, and then keep alternating between the two until the resulting values both converge to fixed points. It's not obvious that this will work, but it can be proven in this context. Additionally, it can be proven that the derivative of the likelihood is (arbitrarily close to) zero at that point, which in turn means that the point is either a local maximum or a saddle point. In general, multiple maxima may occur, with no guarantee that the global maximum will be found. Some likelihoods also have singularities in them, i.e., nonsensical maxima. For example, one of the solutions that may be found by EM in a mixture model involves setting one of the components to have zero variance and the mean parameter for the same component to be equal to one of the data points.

Description

Given the statistical model which generates a set ${\displaystyle \mathbf {X} }$ of observed data, a set of unobserved latent data or missing values ${\displaystyle \mathbf {Z} }$, and a vector of unknown parameters ${\displaystyle {\boldsymbol {\theta }}}$, along with a likelihood function ${\displaystyle L({\boldsymbol {\theta }};\mathbf {X} ,\mathbf {Z} )=p(\mathbf {X} ,\mathbf {Z} \mid {\boldsymbol {\theta }})}$, the maximum likelihood estimate (MLE) of the unknown parameters is determined by maximizing the marginal likelihood of the observed data

${\displaystyle L({\boldsymbol {\theta }};\mathbf {X} )=p(\mathbf {X} \mid {\boldsymbol {\theta }})=\int p(\mathbf {X} ,\mathbf {Z} \mid {\boldsymbol {\theta }})\,d\mathbf {Z} =\int p(\mathbf {X} \mid \mathbf {Z} ,{\boldsymbol {\theta }})p(\mathbf {Z} \mid {\boldsymbol {\theta }})\,d\mathbf {Z} }$

However, this quantity is often intractable since ${\displaystyle \mathbf {Z} }$ is unobserved and the distribution of ${\displaystyle \mathbf {Z} }$ is unknown before attaining ${\displaystyle {\boldsymbol {\theta }}}$.

The EM algorithm seeks to find the MLE of the marginal likelihood by iteratively applying these two steps:

Expectation step (E step): Define ${\displaystyle Q({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})}$ as the expected value of the log likelihood function of ${\displaystyle {\boldsymbol {\theta }}}$, with respect to the current conditional distribution of ${\displaystyle \mathbf {Z} }$ given ${\displaystyle \mathbf {X} }$ and the current estimates of the parameters ${\displaystyle {\boldsymbol {\theta }}^{(t)}}$:

${\displaystyle Q({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})=\operatorname {E} _{\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}^{(t)}}\left[\log L({\boldsymbol {\theta }};\mathbf {X} ,\mathbf {Z} )\right]\,}$

Maximization step (M step): Find the parameters that maximize this quantity:

${\displaystyle {\boldsymbol {\theta }}^{(t+1)}={\underset {\boldsymbol {\theta }}{\operatorname {arg\,max} }}\ Q({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})\,}$

The typical models to which EM is applied use ${\displaystyle \mathbf {Z} }$ as a latent variable indicating membership in one of a set of groups:

1. The observed data points ${\displaystyle \mathbf {X} }$ may be discrete (taking values in a finite or countably infinite set) or continuous (taking values in an uncountably infinite set). Associated with each data point may be a vector of observations.
2. The missing values (aka latent variables) ${\displaystyle \mathbf {Z} }$ are discrete, drawn from a fixed number of values, and with one latent variable per observed unit.
3. The parameters are continuous, and are of two kinds: Parameters that are associated with all data points, and those associated with a specific value of a latent variable (i.e., associated with all data points whose corresponding latent variable has that value).

However, it is possible to apply EM to other sorts of models.

The motivation is as follows. If the value of the parameters ${\displaystyle {\boldsymbol {\theta }}}$ is known, usually the value of the latent variables ${\displaystyle \mathbf {Z} }$ can be found by maximizing the log-likelihood over all possible values of ${\displaystyle \mathbf {Z} }$, either simply by iterating over ${\displaystyle \mathbf {Z} }$ or through an algorithm such as the Viterbi algorithm for hidden Markov models. Conversely, if we know the value of the latent variables ${\displaystyle \mathbf {Z} }$, we can find an estimate of the parameters ${\displaystyle {\boldsymbol {\theta }}}$ fairly easily, typically by simply grouping the observed data points according to the value of the associated latent variable and averaging the values, or some function of the values, of the points in each group. This suggests an iterative algorithm, in the case where both ${\displaystyle {\boldsymbol {\theta }}}$ and ${\displaystyle \mathbf {Z} }$ are unknown:

1. First, initialize the parameters ${\displaystyle {\boldsymbol {\theta }}}$ to some random values.
2. Compute the probability of each possible value of ${\displaystyle \mathbf {Z} }$ , given ${\displaystyle {\boldsymbol {\theta }}}$.
3. Then, use the just-computed values of ${\displaystyle \mathbf {Z} }$ to compute a better estimate for the parameters ${\displaystyle {\boldsymbol {\theta }}}$.
4. Iterate steps 2 and 3 until convergence.

The algorithm as just described monotonically approaches a local minimum of the cost function.

Properties

Speaking of an expectation (E) step is a bit of a misnomer. What are calculated in the first step are the fixed, data-dependent parameters of the function ${\displaystyle Q}$. Once the parameters of ${\displaystyle Q}$ are known, it is fully determined and is maximized in the second (M) step of an EM algorithm.

Although an EM iteration does increase the observed data (i.e., marginal) likelihood function, no guarantee exists that the sequence converges to a maximum likelihood estimator. For multimodal distributions, this means that an EM algorithm may converge to a local maximum of the observed data likelihood function, depending on starting values. A variety of heuristic or metaheuristic approaches exist to escape a local maximum, such as random-restart hill climbing (starting with several different random initial estimates ${\displaystyle {\boldsymbol {\theta }}^{(t)}}$), or applying simulated annealing methods.

EM is especially useful when the likelihood is an exponential family: the E step becomes the sum of expectations of sufficient statistics, and the M step involves maximizing a linear function. In such a case, it is usually possible to derive closed-form expression updates for each step, using the Sundberg formula (published by Rolf Sundberg using unpublished results of Per Martin-Löf and Anders Martin-Löf).

The EM method was modified to compute maximum a posteriori (MAP) estimates for Bayesian inference in the original paper by Dempster, Laird, and Rubin.

Other methods exist to find maximum likelihood estimates, such as gradient descent, conjugate gradient, or variants of the Gauss–Newton algorithm. Unlike EM, such methods typically require the evaluation of first and/or second derivatives of the likelihood function.

Proof of correctness

Expectation-Maximization works to improve ${\displaystyle Q({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})}$ rather than directly improving ${\displaystyle \log p(\mathbf {X} \mid {\boldsymbol {\theta }})}$. Here it is shown that improvements to the former imply improvements to the latter.

For any ${\displaystyle \mathbf {Z} }$ with non-zero probability ${\displaystyle p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }})}$, we can write

${\displaystyle \log p(\mathbf {X} \mid {\boldsymbol {\theta }})=\log p(\mathbf {X} ,\mathbf {Z} \mid {\boldsymbol {\theta }})-\log p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}).}$

We take the expectation over possible values of the unknown data ${\displaystyle \mathbf {Z} }$ under the current parameter estimate ${\displaystyle \theta ^{(t)}}$ by multiplying both sides by ${\displaystyle p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}^{(t)})}$ and summing (or integrating) over ${\displaystyle \mathbf {Z} }$. The left-hand side is the expectation of a constant, so we get:

${\displaystyle {\begin{aligned}\log p(\mathbf {X} \mid {\boldsymbol {\theta }})&=\sum _{\mathbf {Z} }p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}^{(t)})\log p(\mathbf {X} ,\mathbf {Z} \mid {\boldsymbol {\theta }})-\sum _{\mathbf {Z} }p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }}^{(t)})\log p(\mathbf {Z} \mid \mathbf {X} ,{\boldsymbol {\theta }})\\&=Q({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})+H({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)}),\end{aligned}}}$

where ${\displaystyle H({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})}$ is defined by the negated sum it is replacing. This last equation holds for every value of ${\displaystyle {\boldsymbol {\theta }}}$ including ${\displaystyle {\boldsymbol {\theta }}={\boldsymbol {\theta }}^{(t)}}$,

${\displaystyle \log p(\mathbf {X} \mid {\boldsymbol {\theta }}^{(t)})=Q({\boldsymbol {\theta }}^{(t)}\mid {\boldsymbol {\theta }}^{(t)})+H({\boldsymbol {\theta }}^{(t)}\mid {\boldsymbol {\theta }}^{(t)}),}$

and subtracting this last equation from the previous equation gives

${\displaystyle \log p(\mathbf {X} \mid {\boldsymbol {\theta }})-\log p(\mathbf {X} \mid {\boldsymbol {\theta }}^{(t)})=Q({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})-Q({\boldsymbol {\theta }}^{(t)}\mid {\boldsymbol {\theta }}^{(t)})+H({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})-H({\boldsymbol {\theta }}^{(t)}\mid {\boldsymbol {\theta }}^{(t)}),}$

However, Gibbs' inequality tells us that ${\displaystyle H({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})\geq H({\boldsymbol {\theta }}^{(t)}\mid {\boldsymbol {\theta }}^{(t)})}$, so we can conclude that

${\displaystyle \log p(\mathbf {X} \mid {\boldsymbol {\theta }})-\log p(\mathbf {X} \mid {\boldsymbol {\theta }}^{(t)})\geq Q({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})-Q({\boldsymbol {\theta }}^{(t)}\mid {\boldsymbol {\theta }}^{(t)}).}$

In words, choosing ${\displaystyle {\boldsymbol {\theta }}}$ to improve ${\displaystyle Q({\boldsymbol {\theta }}\mid {\boldsymbol {\theta }}^{(t)})}$ causes ${\displaystyle \log p(\mathbf {X} \mid {\boldsymbol {\theta }})}$ to improve at least as much.

As a maximization–maximization procedure

The EM algorithm can be viewed as two alternating maximization steps, that is, as an example of coordinate descent. Consider the function:

${\displaystyle F(q,\theta ):=\operatorname {E} _{q}[\log L(\theta ;x,Z)]+H(q),}$

where q is an arbitrary probability distribution over the unobserved data z and H(q) is the entropy of the distribution q. This function can be written as

${\displaystyle F(q,\theta )=-D_{\mathrm {KL} }{\big (}q\parallel p_{Z\mid X}(\cdot \mid x;\theta ){\big )}+\log L(\theta ;x),}$

where ${\displaystyle p_{Z\mid X}(\cdot \mid x;\theta )}$ is the conditional distribution of the unobserved data given the observed data ${\displaystyle x}$ and ${\displaystyle D_{KL}}$ is the Kullback–Leibler divergence.

Then the steps in the EM algorithm may be viewed as:

Expectation step: Choose ${\displaystyle q}$ to maximize ${\displaystyle F}$:

${\displaystyle q^{(t)}=\operatorname {arg\,max} _{q}\ F(q,\theta ^{(t)})}$

Maximization step: Choose ${\displaystyle \theta }$ to maximize ${\displaystyle F}$:

${\displaystyle \theta ^{(t+1)}=\operatorname {arg\,max} _{\theta }\ F(q^{(t)},\theta )}$

Applications

EM is frequently used for parameter estimation of mixed models, notably in quantitative genetics.

In psychometrics, EM is an important tool for estimating item parameters and latent abilities of item response theory models.

With the ability to deal with missing data and observe unidentified variables, EM is becoming a useful tool to price and manage risk of a portfolio.

The EM algorithm (and its faster variant ordered subset expectation maximization) is also widely used in medical image reconstruction, especially in positron emission tomography, single-photon emission computed tomography, and x-ray computed tomography. See below for other faster variants of EM.

In structural engineering, the Structural Identification using Expectation Maximization (STRIDE) algorithm is an output-only method for identifying natural vibration properties of a structural system using sensor data (see Operational Modal Analysis).

EM is also used for data clustering. In natural language processing, two prominent instances of the algorithm are the Baum–Welch algorithm for hidden Markov models, and the inside-outside algorithm for unsupervised induction of probabilistic context-free grammars.

Filtering and smoothing EM algorithms

A Kalman filter is typically used for on-line state estimation and a minimum-variance smoother may be employed for off-line or batch state estimation. However, these minimum-variance solutions require estimates of the state-space model parameters. EM algorithms can be used for solving joint state and parameter estimation problems.

Filtering and smoothing EM algorithms arise by repeating this two-step procedure:

E-step

Operate a Kalman filter or a minimum-variance smoother designed with current parameter estimates to obtain updated state estimates.

M-step

Use the filtered or smoothed state estimates within maximum-likelihood calculations to obtain updated parameter estimates.

Suppose that a Kalman filter or minimum-variance smoother operates on measurements of a single-input-single-output system that possess additive white noise. An updated measurement noise variance estimate can be obtained from the maximum likelihood calculation

${\displaystyle {\widehat {\sigma }}_{v}^{2}={\frac {1}{N}}\sum _{k=1}^{N}{(z_{k}-{\widehat {x}}_{k})}^{2},}$

where ${\displaystyle {\widehat {x}}_{k}}$ are scalar output estimates calculated by a filter or a smoother from N scalar measurements ${\displaystyle z_{k}}$. The above update can also be applied to updating a Poisson measurement noise intensity. Similarly, for a first-order auto-regressive process, an updated process noise variance estimate can be calculated by

${\displaystyle {\widehat {\sigma }}_{w}^{2}={\frac {1}{N}}\sum _{k=1}^{N}{({\widehat {x}}_{k+1}-{\widehat {F}}{\widehat {x}}_{k})}^{2},}$

where ${\displaystyle {\widehat {x}}_{k}}$ and ${\displaystyle {\widehat {x}}_{k+1}}$ are scalar state estimates calculated by a filter or a smoother. The updated model coefficient estimate is obtained via

${\displaystyle {\widehat {F}}={\frac {\sum _{k=1}^{N}{({\widehat {x}}_{k+1}-{\widehat {F}}{\widehat {x}}_{k})}^{2}}{\sum _{k=1}^{N}{\widehat {x}}_{k}^{2}}}.}$

The convergence of parameter estimates such as those above are well studied.

Variants

A number of methods have been proposed to accelerate the sometimes slow convergence of the EM algorithm, such as those using conjugate gradient and modified Newton's methods (Newton–Raphson). Also, EM can be used with constrained estimation methods.

Parameter-expanded expectation maximization (PX-EM) algorithm often provides speed up by "us[ing] a `covariance adjustment' to correct the analysis of the M step, capitalising on extra information captured in the imputed complete data".

Expectation conditional maximization (ECM) replaces each M step with a sequence of conditional maximization (CM) steps in which each parameter θ_i is maximized individually, conditionally on the other parameters remaining fixed. Itself can be extended into the Expectation conditional maximization either (ECME) algorithm.

This idea is further extended in generalized expectation maximization (GEM) algorithm, in which is sought only an increase in the objective function F for both the E step and M step as described in the As a maximization–maximization procedure section. GEM is further developed in a distributed environment and shows promising results.

It is also possible to consider the EM algorithm as a subclass of the MM (Majorize/Minimize or Minorize/Maximize, depending on context) algorithm, and therefore use any machinery developed in the more general case.

α-EM algorithm

The Q-function used in the EM algorithm is based on the log likelihood. Therefore, it is regarded as the log-EM algorithm. The use of the log likelihood can be generalized to that of the α-log likelihood ratio. Then, the α-log likelihood ratio of the observed data can be exactly expressed as equality by using the Q-function of the α-log likelihood ratio and the α-divergence. Obtaining this Q-function is a generalized E step. Its maximization is a generalized M step. This pair is called the α-EM algorithm which contains the log-EM algorithm as its subclass. Thus, the α-EM algorithm by Yasuo Matsuyama is an exact generalization of the log-EM algorithm. No computation of gradient or Hessian matrix is needed. The α-EM shows faster convergence than the log-EM algorithm by choosing an appropriate α. The α-EM algorithm leads to a faster version of the Hidden Markov model estimation algorithm α-HMM. 

Relation to variational Bayes methods

EM is a partially non-Bayesian, maximum likelihood method. Its final result gives a probability distribution over the latent variables (in the Bayesian style) together with a point estimate for θ (either a maximum likelihood estimate or a posterior mode). A fully Bayesian version of this may be wanted, giving a probability distribution over θ and the latent variables. The Bayesian approach to inference is simply to treat θ as another latent variable. In this paradigm, the distinction between the E and M steps disappears. If using the factorized Q approximation as described above (variational Bayes), solving can iterate over each latent variable (now including θ) and optimize them one at a time. Now, k steps per iteration are needed, where k is the number of latent variables. For graphical models this is easy to do as each variable's new Q depends only on its Markov blanket, so local message passing can be used for efficient inference.

Geometric interpretation

Further information: Information geometry

In information geometry, the E step and the M step are interpreted as projections under dual affine connections, called the e-connection and the m-connection; the Kullback–Leibler divergence can also be understood in these terms.

Examples

Gaussian mixture

Comparison of k-means and EM on artificial data visualized with ELKI. Using the variances, the EM algorithm can describe the normal distributions exactly, while k-means splits the data in Voronoi-cells. The cluster center is indicated by the lighter, bigger symbol.

 

An animation demonstrating the EM algorithm fitting a two component Gaussian mixture model to the Old Faithful dataset. The algorithm steps through from a random initialization to convergence.

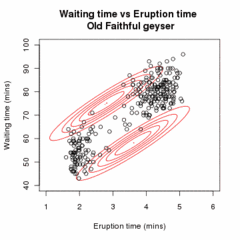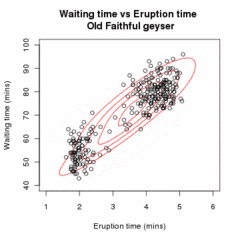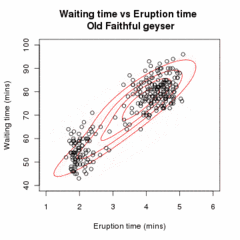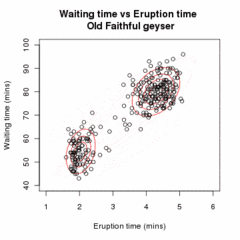
Let ${\displaystyle \mathbf {x} =(\mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{n})}$ be a sample of ${\displaystyle n}$ independent observations from a mixture of two multivariate normal distributions of dimension ${\displaystyle d}$, and let ${\displaystyle \mathbf {z} =(z_{1},z_{2},\ldots ,z_{n})}$ be the latent variables that determine the component from which the observation originates.

and ${\displaystyle X_{i}\mid (Z_{i}=2)\sim {\mathcal {N}}_{d}({\boldsymbol {\mu }}_{2},\Sigma _{2}),}$

where

${\displaystyle \operatorname {P} (Z_{i}=1)=\tau _{1}\,}$ and ${\displaystyle \operatorname {P} (Z_{i}=2)=\tau _{2}=1-\tau _{1}.}$

The aim is to estimate the unknown parameters representing the mixing value between the Gaussians and the means and covariances of each:

${\displaystyle \theta ={\big (}{\boldsymbol {\tau }},{\boldsymbol {\mu }}_{1},{\boldsymbol {\mu }}_{2},\Sigma _{1},\Sigma _{2}{\big )},}$

where the incomplete-data likelihood function is

${\displaystyle L(\theta ;\mathbf {x} )=\prod _{i=1}^{n}\sum _{j=1}^{2}\tau _{j}\ f(\mathbf {x} _{i};{\boldsymbol {\mu }}_{j},\Sigma _{j}),}$

and the complete-data likelihood function is

${\displaystyle L(\theta ;\mathbf {x} ,\mathbf {z} )=p(\mathbf {x} ,\mathbf {z} \mid \theta )=\prod _{i=1}^{n}\prod _{j=1}^{2}\ [f(\mathbf {x} _{i};{\boldsymbol {\mu }}_{j},\Sigma _{j})\tau _{j}]^{\mathbb {I} (z_{i}=j)},}$

or

${\displaystyle L(\theta ;\mathbf {x} ,\mathbf {z} )=\exp \left\{\sum _{i=1}^{n}\sum _{j=1}^{2}\mathbb {I} (z_{i}=j){\big [}\log \tau _{j}-{\tfrac {1}{2}}\log |\Sigma _{j}|-{\tfrac {1}{2}}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{j})^{\top }\Sigma _{j}^{-1}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{j})-{\tfrac {d}{2}}\log(2\pi ){\big ]}\right\},}$

where ${\displaystyle \mathbb {I} }$ is an indicator function and ${\displaystyle f}$ is the probability density function of a multivariate normal.

In the last equality, for each i, one indicator ${\displaystyle \mathbb {I} (z_{i}=j)}$ is equal to zero, and one indicator is equal to one. The inner sum thus reduces to one term.

E step

Given our current estimate of the parameters θ^(t), the conditional distribution of the Z_i is determined by Bayes theorem to be the proportional height of the normal density weighted by τ:

${\displaystyle T_{j,i}^{(t)}:=\operatorname {P} (Z_{i}=j\mid X_{i}=\mathbf {x} _{i};\theta ^{(t)})={\frac {\tau _{j}^{(t)}\ f(\mathbf {x} _{i};{\boldsymbol {\mu }}_{j}^{(t)},\Sigma _{j}^{(t)})}{\tau _{1}^{(t)}\ f(\mathbf {x} _{i};{\boldsymbol {\mu }}_{1}^{(t)},\Sigma _{1}^{(t)})+\tau _{2}^{(t)}\ f(\mathbf {x} _{i};{\boldsymbol {\mu }}_{2}^{(t)},\Sigma _{2}^{(t)})}}.}$

These are called the "membership probabilities", which are normally considered the output of the E step (although this is not the Q function of below).

This E step corresponds with setting up this function for Q:

${\displaystyle {\begin{aligned}Q(\theta \mid \theta ^{(t)})&=\operatorname {E} _{\mathbf {Z} \mid \mathbf {X} ,\mathbf {\theta } ^{(t)}}[\log L(\theta ;\mathbf {x} ,\mathbf {Z} )]\\&=\operatorname {E} _{\mathbf {Z} \mid \mathbf {X} ,\mathbf {\theta } ^{(t)}}[\log \prod _{i=1}^{n}L(\theta ;\mathbf {x} _{i},Z_{i})]\\&=\operatorname {E} _{\mathbf {Z} \mid \mathbf {X} ,\mathbf {\theta } ^{(t)}}[\sum _{i=1}^{n}\log L(\theta ;\mathbf {x} _{i},Z_{i})]\\&=\sum _{i=1}^{n}\operatorname {E} _{Z_{i}\mid \mathbf {X} ;\mathbf {\theta } ^{(t)}}[\log L(\theta ;\mathbf {x} _{i},Z_{i})]\\&=\sum _{i=1}^{n}\sum _{j=1}^{2}P(Z_{i}=j\mid X_{i}=\mathbf {x} _{i};\theta ^{(t)})\log L(\theta _{j};\mathbf {x} _{i},j)\\&=\sum _{i=1}^{n}\sum _{j=1}^{2}T_{j,i}^{(t)}{\big [}\log \tau _{j}-{\tfrac {1}{2}}\log |\Sigma _{j}|-{\tfrac {1}{2}}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{j})^{\top }\Sigma _{j}^{-1}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{j})-{\tfrac {d}{2}}\log(2\pi ){\big ]}.\end{aligned}}}$

The expectation of ${\displaystyle \log L(\theta ;\mathbf {x} _{i},Z_{i})}$ inside the sum is taken with respect to the probability density function ${\displaystyle P(Z_{i}\mid X_{i}=\mathbf {x} _{i};\theta ^{(t)})}$, which might be different for each ${\displaystyle \mathbf {x} _{i}}$ of the training set. Everything in the E step is known before the step is taken except ${\displaystyle T_{j,i}}$, which is computed according to the equation at the beginning of the E step section.

This full conditional expectation does not need to be calculated in one step, because τ and μ/Σ appear in separate linear terms and can thus be maximized independently.

M step

Q(θ | θ^(t)) being quadratic in form means that determining the maximizing values of θ is relatively straightforward. Also, τ, (μ₁,Σ₁) and (μ₂,Σ₂) may all be maximized independently since they all appear in separate linear terms.

To begin, consider τ, which has the constraint τ₁ + τ₂=1:

${\displaystyle {\begin{aligned}{\boldsymbol {\tau }}^{(t+1)}&={\underset {\boldsymbol {\tau }}{\operatorname {arg\,max} }}\ Q(\theta \mid \theta ^{(t)})\\&={\underset {\boldsymbol {\tau }}{\operatorname {arg\,max} }}\ \left\{\left[\sum _{i=1}^{n}T_{1,i}^{(t)}\right]\log \tau _{1}+\left[\sum _{i=1}^{n}T_{2,i}^{(t)}\right]\log \tau _{2}\right\}.\end{aligned}}}$

This has the same form as the MLE for the binomial distribution, so

${\displaystyle \tau _{j}^{(t+1)}={\frac {\sum _{i=1}^{n}T_{j,i}^{(t)}}{\sum _{i=1}^{n}(T_{1,i}^{(t)}+T_{2,i}^{(t)})}}={\frac {1}{n}}\sum _{i=1}^{n}T_{j,i}^{(t)}.}$

For the next estimates of (μ₁,Σ₁):

${\displaystyle {\begin{aligned}({\boldsymbol {\mu }}_{1}^{(t+1)},\Sigma _{1}^{(t+1)})&={\underset {{\boldsymbol {\mu }}_{1},\Sigma _{1}}{\operatorname {arg\,max} }}\ Q(\theta \mid \theta ^{(t)})\\&={\underset {{\boldsymbol {\mu }}_{1},\Sigma _{1}}{\operatorname {arg\,max} }}\ \sum _{i=1}^{n}T_{1,i}^{(t)}\left\{-{\tfrac {1}{2}}\log |\Sigma _{1}|-{\tfrac {1}{2}}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{1})^{\top }\Sigma _{1}^{-1}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{1})\right\}\end{aligned}}.}$

This has the same form as a weighted MLE for a normal distribution, so

${\displaystyle {\boldsymbol {\mu }}_{1}^{(t+1)}={\frac {\sum _{i=1}^{n}T_{1,i}^{(t)}\mathbf {x} _{i}}{\sum _{i=1}^{n}T_{1,i}^{(t)}}}}$ and ${\displaystyle \Sigma _{1}^{(t+1)}={\frac {\sum _{i=1}^{n}T_{1,i}^{(t)}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{1}^{(t+1)})(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{1}^{(t+1)})^{\top }}{\sum _{i=1}^{n}T_{1,i}^{(t)}}}}$

and, by symmetry,

${\displaystyle {\boldsymbol {\mu }}_{2}^{(t+1)}={\frac {\sum _{i=1}^{n}T_{2,i}^{(t)}\mathbf {x} _{i}}{\sum _{i=1}^{n}T_{2,i}^{(t)}}}}$ and ${\displaystyle \Sigma _{2}^{(t+1)}={\frac {\sum _{i=1}^{n}T_{2,i}^{(t)}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{2}^{(t+1)})(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{2}^{(t+1)})^{\top }}{\sum _{i=1}^{n}T_{2,i}^{(t)}}}.}$

Termination

Conclude the iterative process if ${\displaystyle E_{Z\mid \theta ^{(t)},\mathbf {x} }[\log L(\theta ^{(t)};\mathbf {x} ,\mathbf {Z} )]\leq E_{Z\mid \theta ^{(t-1)},\mathbf {x} }[\log L(\theta ^{(t-1)};\mathbf {x} ,\mathbf {Z} )]+\varepsilon }$ for ${\displaystyle \varepsilon }$ below some preset threshold.

Generalization

The algorithm illustrated above can be generalized for mixtures of more than two multivariate normal distributions.

Truncated and censored regression

The EM algorithm has been implemented in the case where an underlying linear regression model exists explaining the variation of some quantity, but where the values actually observed are censored or truncated versions of those represented in the model. Special cases of this model include censored or truncated observations from one normal distribution.

Alternatives

EM typically converges to a local optimum, not necessarily the global optimum, with no bound on the convergence rate in general. It is possible that it can be arbitrarily poor in high dimensions and there can be an exponential number of local optima. Hence, a need exists for alternative methods for guaranteed learning, especially in the high-dimensional setting. Alternatives to EM exist with better guarantees for consistency, which are termed moment-based approaches or the so-called spectral techniques. Moment-based approaches to learning the parameters of a probabilistic model are of increasing interest recently since they enjoy guarantees such as global convergence under certain conditions unlike EM which is often plagued by the issue of getting stuck in local optima. Algorithms with guarantees for learning can be derived for a number of important models such as mixture models, HMMs etc. For these spectral methods, no spurious local optima occur, and the true parameters can be consistently estimated under some regularity conditions.

Center of mass

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Center_of_mass 

 

This toy uses the principles of center of mass to keep balance when sitting on a finger.

In physics, the center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative position of the distributed mass sums to zero. This is the point to which a force may be applied to cause a linear acceleration without an angular acceleration. Calculations in mechanics are often simplified when formulated with respect to the center of mass. It is a hypothetical point where the entire mass of an object may be assumed to be concentrated to visualise its motion. In other words, the center of mass is the particle equivalent of a given object for application of Newton's laws of motion.

In the case of a single rigid body, the center of mass is fixed in relation to the body, and if the body has uniform density, it will be located at the centroid. The center of mass may be located outside the physical body, as is sometimes the case for hollow or open-shaped objects, such as a horseshoe. In the case of a distribution of separate bodies, such as the planets of the Solar System, the center of mass may not correspond to the position of any individual member of the system.

The center of mass is a useful reference point for calculations in mechanics that involve masses distributed in space, such as the linear and angular momentum of planetary bodies and rigid body dynamics. In orbital mechanics, the equations of motion of planets are formulated as point masses located at the centers of mass. The center of mass frame is an inertial frame in which the center of mass of a system is at rest with respect to the origin of the coordinate system.

History

The concept of center of gravity or weight was studied extensively by the ancient Greek mathematician, physicist, and engineer Archimedes of Syracuse. He worked with simplified assumptions about gravity that amount to a uniform field, thus arriving at the mathematical properties of what we now call the center of mass. Archimedes showed that the torque exerted on a lever by weights resting at various points along the lever is the same as what it would be if all of the weights were moved to a single point—their center of mass. In his work On Floating Bodies, Archimedes demonstrated that the orientation of a floating object is the one that makes its center of mass as low as possible. He developed mathematical techniques for finding the centers of mass of objects of uniform density of various well-defined shapes.

Other ancient mathematicians who contributed to the theory of the center of mass include Hero of Alexandria and Pappus of Alexandria. In the Renaissance and Early Modern periods, work by Guido Ubaldi, Francesco Maurolico, Federico Commandino, Evangelista Torricelli, Simon Stevin, Luca Valerio, Jean-Charles de la Faille, Paul Guldin, John Wallis, Christiaan Huygens, Louis Carré, Pierre Varignon, and Alexis Clairaut expanded the concept further.

Newton's second law is reformulated with respect to the center of mass in Euler's first law.

Definition

The center of mass is the unique point at the center of a distribution of mass in space that has the property that the weighted position vectors relative to this point sum to zero. In analogy to statistics, the center of mass is the mean location of a distribution of mass in space.

A system of particles

In the case of a system of particles P_i, i = 1, ..., n , each with mass m_i that are located in space with coordinates r_i, i = 1, ..., n , the coordinates R of the center of mass satisfy the condition

$${\displaystyle \sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )=\mathbf {0} .}$$

Solving this equation for R yields the formula

$${\displaystyle \mathbf {R} ={\frac {1}{M}}\sum _{i=1}^{n}m_{i}\mathbf {r} _{i},}$$

where ${\displaystyle M=\sum _{i=1}^{n}m_{i}}$ is the total mass of all of the particles.

A continuous volume

If the mass distribution is continuous with the density ρ(r) within a solid Q, then the integral of the weighted position coordinates of the points in this volume relative to the center of mass R over the volume V is zero, that is

$${\displaystyle \iiint _{Q}\rho (\mathbf {r} )\left(\mathbf {r} -\mathbf {R} \right)dV=0.}$$

Solve this equation for the coordinates R to obtain

$${\displaystyle \mathbf {R} ={\frac {1}{M}}\iiint _{Q}\rho (\mathbf {r} )\mathbf {r} \,dV,}$$

where M is the total mass in the volume.

If a continuous mass distribution has uniform density, which means ρ is constant, then the center of mass is the same as the centroid of the volume.

Barycentric coordinates

Further information: Barycentric coordinate system

The coordinates R of the center of mass of a two-particle system, P₁ and P₂, with masses m₁ and m₂ is given by

$${\displaystyle \mathbf {R} ={\frac {1}{m_{1}+m_{2}}}(m_{1}\mathbf {r} _{1}+m_{2}\mathbf {r} _{2}).}$$

Let the percentage of the total mass divided between these two particles vary from 100% P₁ and 0% P₂ through 50% P₁ and 50% P₂ to 0% P₁ and 100% P₂, then the center of mass R moves along the line from P₁ to P₂. The percentages of mass at each point can be viewed as projective coordinates of the point R on this line, and are termed barycentric coordinates. Another way of interpreting the process here is the mechanical balancing of moments about an arbitrary point. The numerator gives the total moment that is then balanced by an equivalent total force at the center of mass. This can be generalized to three points and four points to define projective coordinates in the plane, and in space, respectively.

Systems with periodic boundary conditions

For particles in a system with periodic boundary conditions two particles can be neighbours even though they are on opposite sides of the system. This occurs often in molecular dynamics simulations, for example, in which clusters form at random locations and sometimes neighbouring atoms cross the periodic boundary. When a cluster straddles the periodic boundary, a naive calculation of the center of mass will be incorrect. A generalized method for calculating the center of mass for periodic systems is to treat each coordinate, x and y and/or z, as if it were on a circle instead of a line. The calculation takes every particle's x coordinate and maps it to an angle,

$${\displaystyle \theta _{i}={\frac {x_{i}}{x_{\max }}}2\pi }$$

where x_max is the system size in the x direction and ${\displaystyle x_{i}\in [0,x_{\max })}$. From this angle, two new points ${\displaystyle (\xi _{i},\zeta _{i})}$ can be generated, which can be weighted by the mass of the particle ${\displaystyle x_{i}}$ for the center of mass or given a value of 1 for the geometric center:

$${\displaystyle {\begin{aligned}\xi _{i}&=\cos(\theta _{i})\\\zeta _{i}&=\sin(\theta _{i})\end{aligned}}}$$

In the ${\displaystyle (\xi ,\zeta )}$ plane, these coordinates lie on a circle of radius 1. From the collection of ${\displaystyle \xi _{i}}$ and ${\displaystyle \zeta _{i}}$ values from all the particles, the averages ${\displaystyle {\overline {\xi }}}$ and ${\displaystyle {\overline {\zeta }}}$ are calculated.

$${\displaystyle {\begin{aligned}{\overline {\xi }}&={\frac {1}{M}}\sum _{i=1}^{n}m_{i}\xi _{i},\\{\overline {\zeta }}&={\frac {1}{M}}\sum _{i=1}^{n}m_{i}\zeta _{i},\end{aligned}}}$$

where M is the sum of the masses of all of the particles.

These values are mapped back into a new angle, ${\displaystyle {\overline {\theta }}}$, from which the x coordinate of the center of mass can be obtained:

$${\displaystyle {\begin{aligned}{\overline {\theta }}&=\operatorname {atan2} \left(-{\overline {\zeta }},-{\overline {\xi }}\right)+\pi \\x_{\text{com}}&=x_{\max }{\frac {\overline {\theta }}{2\pi }}\end{aligned}}}$$

The process can be repeated for all dimensions of the system to determine the complete center of mass. The utility of the algorithm is that it allows the mathematics to determine where the "best" center of mass is, instead of guessing or using cluster analysis to "unfold" a cluster straddling the periodic boundaries. If both average values are zero, ${\displaystyle \left({\overline {\xi }},{\overline {\zeta }}\right)=(0,0)}$, then ${\displaystyle {\overline {\theta }}}$ is undefined. This is a correct result, because it only occurs when all particles are exactly evenly spaced. In that condition, their x coordinates are mathematically identical in a periodic system.

Center of gravity

"Center of gravity" redirects here. For other uses, see Center of gravity (disambiguation).

 

Main article: Centers of gravity in non-uniform fields

 

Diagram of an educational toy that balances on a point: the center of mass (C) settles below its support (P)

A body's center of gravity is the point around which the resultant torque due to gravity forces vanishes. Where a gravity field can be considered to be uniform, the mass-center and the center-of-gravity will be the same. However, for satellites in orbit around a planet, in the absence of other torques being applied to a satellite, the slight variation (gradient) in gravitational field between closer-to (stronger) and further-from (weaker) the planet can lead to a torque that will tend to align the satellite such that its long axis is vertical. In such a case, it is important to make the distinction between the center-of-gravity and the mass-center. Any horizontal offset between the two will result in an applied torque.

It is useful to note that the mass-center is a fixed property for a given rigid body (e.g. with no slosh or articulation), whereas the center-of-gravity may, in addition, depend upon its orientation in a non-uniform gravitational field. In the latter case, the center-of-gravity will always be located somewhat closer to the main attractive body as compared to the mass-center, and thus will change its position in the body of interest as its orientation is changed.

In the study of the dynamics of aircraft, vehicles and vessels, forces and moments need to be resolved relative to the mass center. That is true independent of whether gravity itself is a consideration. Referring to the mass-center as the center-of-gravity is something of a colloquialism, but it is in common usage and when gravity gradient effects are negligible, center-of-gravity and mass-center are the same and are used interchangeably.

In physics the benefits of using the center of mass to model a mass distribution can be seen by considering the resultant of the gravity forces on a continuous body. Consider a body Q of volume V with density ρ(r) at each point r in the volume. In a parallel gravity field the force f at each point r is given by,

$${\displaystyle \mathbf {f} (\mathbf {r} )=-dm\,g\mathbf {\hat {k}} =-\rho (\mathbf {r} )\,dV\,g\mathbf {\hat {k}} ,}$$

where dm is the mass at the point r, g is the acceleration of gravity, and ${\textstyle \mathbf {\hat {k}} }$ is a unit vector defining the vertical direction.

Choose a reference point R in the volume and compute the resultant force and torque at this point,

$${\displaystyle \mathbf {F} =\iiint _{Q}\mathbf {f} (\mathbf {r} )\,dV=\iiint _{Q}\rho (\mathbf {r} )\,dV\left(-g\mathbf {\hat {k}} \right)=-Mg\mathbf {\hat {k}} ,}$$

and

$${\displaystyle \mathbf {T} =\iiint _{Q}(\mathbf {r} -\mathbf {R} )\times \mathbf {f} (\mathbf {r} )\,dV=\iiint _{Q}(\mathbf {r} -\mathbf {R} )\times \left(-g\rho (\mathbf {r} )\,dV\,\mathbf {\hat {k}} \right)=\left(\iiint _{Q}\rho (\mathbf {r} )\left(\mathbf {r} -\mathbf {R} \right)dV\right)\times \left(-g\mathbf {\hat {k}} \right).}$$

If the reference point R is chosen so that it is the center of mass, then

$${\displaystyle \iiint _{Q}\rho (\mathbf {r} )\left(\mathbf {r} -\mathbf {R} \right)dV=0,}$$

which means the resultant torque T = 0. Because the resultant torque is zero the body will move as though it is a particle with its mass concentrated at the center of mass.

By selecting the center of gravity as the reference point for a rigid body, the gravity forces will not cause the body to rotate, which means the weight of the body can be considered to be concentrated at the center of mass.

Linear and angular momentum

The linear and angular momentum of a collection of particles can be simplified by measuring the position and velocity of the particles relative to the center of mass. Let the system of particles P_i, i = 1, ..., n of masses m_i be located at the coordinates r_i with velocities v_i. Select a reference point R and compute the relative position and velocity vectors,

$${\displaystyle \mathbf {r} _{i}=(\mathbf {r} _{i}-\mathbf {R} )+\mathbf {R} ,\quad \mathbf {v} _{i}={\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+\mathbf {v} .}$$

The total linear momentum and angular momentum of the system are

$${\displaystyle \mathbf {p} ={\frac {d}{dt}}\left(\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\right)+\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {v} ,}$$

and

$${\displaystyle \mathbf {L} =\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\times {\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+\left(\sum _{i=1}^{n}m_{i}\right)\left[\mathbf {R} \times {\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+(\mathbf {r} _{i}-\mathbf {R} )\times \mathbf {v} \right]+\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {R} \times \mathbf {v} }$$

If R is chosen as the center of mass these equations simplify to

$${\displaystyle \mathbf {p} =m\mathbf {v} ,\quad \mathbf {L} =\sum _{i=1}^{n}m_{i}(\mathbf {r} _{i}-\mathbf {R} )\times {\frac {d}{dt}}(\mathbf {r} _{i}-\mathbf {R} )+\sum _{i=1}^{n}m_{i}\mathbf {R} \times \mathbf {v} }$$

where m is the total mass of all the particles, p is the linear momentum, and L is the angular momentum.

The law of conservation of momentum predicts that for any system not subjected to external forces the momentum of the system will remain constant, which means the center of mass will move with constant velocity. This applies for all systems with classical internal forces, including magnetic fields, electric fields, chemical reactions, and so on. More formally, this is true for any internal forces that cancel in accordance with Newton's Third Law.

Locating the center of mass

Main article: Locating the center of mass

 

Plumb line method

The experimental determination of a body's centre of mass makes use of gravity forces on the body and is based on the fact that the centre of mass is the same as the centre of gravity in the parallel gravity field near the earth's surface.

The center of mass of a body with an axis of symmetry and constant density must lie on this axis. Thus, the center of mass of a circular cylinder of constant density has its center of mass on the axis of the cylinder. In the same way, the center of mass of a spherically symmetric body of constant density is at the center of the sphere. In general, for any symmetry of a body, its center of mass will be a fixed point of that symmetry.

In two dimensions

An experimental method for locating the center of mass is to suspend the object from two locations and to drop plumb lines from the suspension points. The intersection of the two lines is the center of mass.

The shape of an object might already be mathematically determined, but it may be too complex to use a known formula. In this case, one can subdivide the complex shape into simpler, more elementary shapes, whose centers of mass are easy to find. If the total mass and center of mass can be determined for each area, then the center of mass of the whole is the weighted average of the centers. This method can even work for objects with holes, which can be accounted for as negative masses.

A direct development of the planimeter known as an integraph, or integerometer, can be used to establish the position of the centroid or center of mass of an irregular two-dimensional shape. This method can be applied to a shape with an irregular, smooth or complex boundary where other methods are too difficult. It was regularly used by ship builders to compare with the required displacement and center of buoyancy of a ship, and ensure it would not capsize.

In three dimensions

An experimental method to locate the three-dimensional coordinates of the center of mass begins by supporting the object at three points and measuring the forces, F₁, F₂, and F₃ that resist the weight of the object, ${\displaystyle \mathbf {W} =-W\mathbf {\hat {k}} }$ (${\displaystyle \mathbf {\hat {k}} }$ is the unit vector in the vertical direction). Let r₁, r₂, and r₃ be the position coordinates of the support points, then the coordinates R of the center of mass satisfy the condition that the resultant torque is zero,

$${\displaystyle \mathbf {T} =(\mathbf {r} _{1}-\mathbf {R} )\times \mathbf {F} _{1}+(\mathbf {r} _{2}-\mathbf {R} )\times \mathbf {F} _{2}+(\mathbf {r} _{3}-\mathbf {R} )\times \mathbf {F} _{3}=0,}$$

or

$${\displaystyle \mathbf {R} \times \left(-W\mathbf {\hat {k}} \right)=\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\mathbf {r} _{3}\times \mathbf {F} _{3}.}$$

This equation yields the coordinates of the center of mass R* in the horizontal plane as,

$${\displaystyle \mathbf {R} ^{*}=-{\frac {1}{W}}\mathbf {\hat {k}} \times (\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\mathbf {r} _{3}\times \mathbf {F} _{3}).}$$

The center of mass lies on the vertical line L, given by

$${\displaystyle \mathbf {L} (t)=\mathbf {R} ^{*}+t\mathbf {\hat {k}} .}$$

The three-dimensional coordinates of the center of mass are determined by performing this experiment twice with the object positioned so that these forces are measured for two different horizontal planes through the object. The center of mass will be the intersection of the two lines L₁ and L₂ obtained from the two experiments.

Applications

Engineering designs

Automotive applications

Engineers try to design a sports car so that its center of mass is lowered to make the car handle better, which is to say, maintain traction while executing relatively sharp turns.

The characteristic low profile of the U.S. military Humvee was designed in part to allow it to tilt farther than taller vehicles without rolling over, by ensuring its low center of mass stays over the space bounded by the four wheels even at angles far from the horizontal.

Aeronautics

Main article: Center of gravity of an aircraft

The center of mass is an important point on an aircraft, which significantly affects the stability of the aircraft. To ensure the aircraft is stable enough to be safe to fly, the center of mass must fall within specified limits. If the center of mass is ahead of the forward limit, the aircraft will be less maneuverable, possibly to the point of being unable to rotate for takeoff or flare for landing. If the center of mass is behind the aft limit, the aircraft will be more maneuverable, but also less stable, and possibly unstable enough so as to be impossible to fly. The moment arm of the elevator will also be reduced, which makes it more difficult to recover from a stalled condition.

For helicopters in hover, the center of mass is always directly below the rotorhead. In forward flight, the center of mass will move forward to balance the negative pitch torque produced by applying cyclic control to propel the helicopter forward; consequently a cruising helicopter flies "nose-down" in level flight.

Astronomy

Main article: Barycenter

 

Two bodies orbiting their barycenter (red cross)

The center of mass plays an important role in astronomy and astrophysics, where it is commonly referred to as the barycenter. The barycenter is the point between two objects where they balance each other; it is the center of mass where two or more celestial bodies orbit each other. When a moon orbits a planet, or a planet orbits a star, both bodies are actually orbiting a point that lies away from the center of the primary (larger) body. For example, the Moon does not orbit the exact center of the Earth, but a point on a line between the center of the Earth and the Moon, approximately 1,710 km (1,062 miles) below the surface of the Earth, where their respective masses balance. This is the point about which the Earth and Moon orbit as they travel around the Sun. If the masses are more similar, e.g., Pluto and Charon, the barycenter will fall outside both bodies.

Rigging and safety

Knowing the location of the center of gravity when rigging is crucial, possibly resulting in severe injury or death if assumed incorrectly. A center of gravity that is at or above the lift point will most likely result in a tip-over incident. In general, the further the center of gravity below the pick point, the more safe the lift. There are other things to consider, such as shifting loads, strength of the load and mass, distance between pick points, and number of pick points. Specifically, when selecting lift points, it's very important to place the center of gravity at the center and well below the lift points.

Body motion

Main article: Kinesiology

In kinesiology and biomechanics, the center of mass is an important parameter that assists people in understanding their human locomotion. Typically, a human's center of mass is detected with one of two methods: the reaction board method is a static analysis that involves the person lying down on that instrument, and use of their static equilibrium equation to find their center of mass; the segmentation method relies on a mathematical solution based on the physical principle that the summation of the torques of individual body sections, relative to a specified axis, must equal the torque of the whole system that constitutes the body, measured relative to the same axis.