p–n junction

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/P%E2%80%93n_junction

 

See also: p–n diode and Diode § Semiconductor diodes

 

A p–n junction. The circuit symbol is shown: the triangle corresponds to the p side.

A p–n junction is a boundary or interface between two types of semiconductor materials, p-type and n-type, inside a single crystal of semiconductor. The "p" (positive) side contains an excess of holes, while the "n" (negative) side contains an excess of electrons in the outer shells of the electrically neutral atoms there. This allows electrical current to pass through the junction only in one direction. The p-n junction is created by doping, for example by ion implantation, diffusion of dopants, or by epitaxy (growing a layer of crystal doped with one type of dopant on top of a layer of crystal doped with another type of dopant).

p–n junctions are elementary "building blocks" of semiconductor electronic devices such as diodes, transistors, solar cells, light-emitting diodes (LEDs), and integrated circuits; they are the active sites where the electronic action of the device takes place. For example, a common type of transistor, the bipolar junction transistor (BJT), consists of two p–n junctions in series, in the form n–p–n or p–n–p; while a diode can be made from a single p-n junction. A Schottky junction is a special case of a p–n junction, where metal serves the role of the n-type semiconductor.

History

The invention of the p–n junction is usually attributed to American physicist Russell Ohl of Bell Laboratories in 1939. Two years later (1941), Vadim Lashkaryov reported discovery of p–n junctions in Cu₂O and silver sulphide photocells and selenium rectifiers.

Properties

Silicon atoms (Si) enlarged about 45,000,000x

The p–n junction possesses a useful property for modern semiconductor electronics. A p-doped semiconductor is relatively conductive. The same is true of an n-doped semiconductor, but the junction between them can become depleted of charge carriers, and hence non-conductive, depending on the relative voltages of the two semiconductor regions. By manipulating this non-conductive layer, p–n junctions are commonly used as diodes: circuit elements that allow a flow of electricity in one direction but not in the other (opposite) direction.

Bias is the application of a voltage relative to a p–n junction region:

• Forward bias is in the direction of easy current flow
• Reverse bias is in the direction of little or no current flow.

The forward-bias and the reverse-bias properties of the p–n junction imply that it can be used as a diode. A p–n junction diode allows electric charges to flow in one direction, but not in the opposite direction; negative charges (electrons) can easily flow through the junction from n to p but not from p to n, and the reverse is true for holes. When the p–n junction is forward-biased, electric charge flows freely due to reduced resistance of the p–n junction. When the p–n junction is reverse-biased, however, the junction barrier (and therefore resistance) becomes greater and charge flow is minimal.

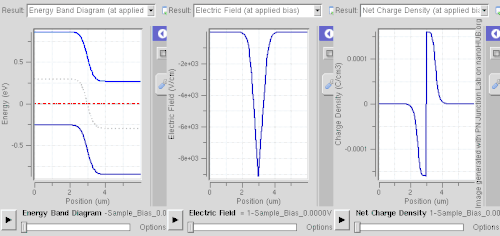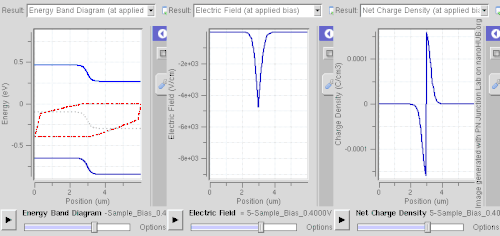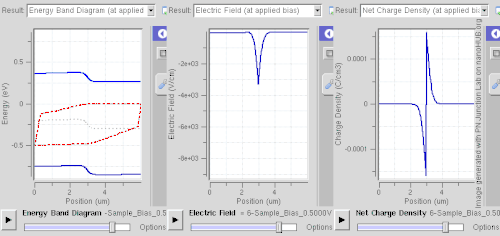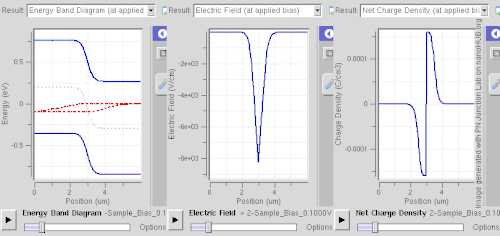
Equilibrium (zero bias)

In a p–n junction, without an external applied voltage, an equilibrium condition is reached in which a potential difference forms across the junction. This potential difference is called built-in potential ${\displaystyle V_{\mathrm{b}\mathrm{i}}}$.

At the junction, some of the free electrons in the n-type wander into the p-type due to random thermal migration. As they diffuse into the p-type they combine with holes, and cancel each other out. In a similar way some of the positive holes in the p-type wander into the n-type and combine with free electrons, and cancel each other out. The positively charged, donor, dopant atoms in the n-type are part of the crystal, and cannot move. Thus, in the n-type, a region near the junction becomes positively charged. The negatively charged, acceptor, dopant atoms in the p-type are part of the crystal, and cannot move. Thus, in the p-type, a region near the junction becomes negatively charged. The result is a region near the junction that acts to repel the mobile charges away from the junction through the electric field that these charged regions create. The regions near the p–n interface lose their neutrality and most of their mobile carriers, forming the space charge region or depletion layer (see figure A).

Figure A. A p–n junction in thermal equilibrium with zero-bias voltage applied. Electron and hole concentration are reported with blue and red lines, respectively. Gray regions are charge-neutral. Light-red zone is positively charged. Light-blue zone is negatively charged. The electric field is shown on the bottom, the electrostatic force on electrons and holes and the direction in which the diffusion tends to move electrons and holes. (The log concentration curves should actually be smoother with slope varying with field strength.)

The electric field created by the space charge region opposes the diffusion process for both electrons and holes. There are two concurrent phenomena: the diffusion process that tends to generate more space charge, and the electric field generated by the space charge that tends to counteract the diffusion. The carrier concentration profile at equilibrium is shown in figure A with blue and red lines. Also shown are the two counterbalancing phenomena that establish equilibrium.

Figure B. A p–n junction in thermal equilibrium with zero-bias voltage applied. Under the junction, plots for the charge density, the electric field, and the voltage are reported. (The log concentration curves should actually be smoother, like the voltage.)

The space charge region is a zone with a net charge provided by the fixed ions (donors or acceptors) that have been left uncovered by majority carrier diffusion. When equilibrium is reached, the charge density is approximated by the displayed step function. In fact, since the y-axis of figure A is log-scale, the region is almost completely depleted of majority carriers (leaving a charge density equal to the net doping level), and the edge between the space charge region and the neutral region is quite sharp (see figure B, Q(x) graph). The space charge region has the same magnitude of charge on both sides of the p–n interfaces, thus it extends farther on the less doped side in this example (the n side in figures A and B).

Forward bias

See also: p–n diode § Forward bias

 

PN junction operation in forward-bias mode, showing reducing depletion width.

In forward bias, the p-type is connected with the positive terminal and the n-type is connected with the negative terminal. The panels show energy band diagram, electric field, and net charge density. Both p and n junctions are doped at a 1e15 cm⁻³ (160 µC/cm³) doping level, leading to built-in potential of ~0.59 V. Reducing depletion width can be inferred from the shrinking carrier motion across the p–n junction, which as a consequence reduces electrical resistance. Electrons that cross the p–n junction into the p-type material (or holes that cross into the n-type material) diffuse into the nearby neutral region. The amount of minority diffusion in the near-neutral zones determines the amount of current that can flow through the diode.

Only majority carriers (electrons in n-type material or holes in p-type) can flow through a semiconductor for a macroscopic length. With this in mind, consider the flow of electrons across the junction. The forward bias causes a force on the electrons pushing them from the N side toward the P side. With forward bias, the depletion region is narrow enough that electrons can cross the junction and inject into the p-type material. However, they do not continue to flow through the p-type material indefinitely, because it is energetically favorable for them to recombine with holes. The average length an electron travels through the p-type material before recombining is called the diffusion length, and it is typically on the order of micrometers.

Although the electrons penetrate only a short distance into the p-type material, the electric current continues uninterrupted, because holes (the majority carriers) begin to flow in the opposite direction. The total current (the sum of the electron and hole currents) is constant in space, because any variation would cause charge buildup over time (this is Kirchhoff's current law). The flow of holes from the p-type region into the n-type region is exactly analogous to the flow of electrons from N to P (electrons and holes swap roles and the signs of all currents and voltages are reversed).

Therefore, the macroscopic picture of the current flow through the diode involves electrons flowing through the n-type region toward the junction, holes flowing through the p-type region in the opposite direction toward the junction, and the two species of carriers constantly recombining in the vicinity of the junction. The electrons and holes travel in opposite directions, but they also have opposite charges, so the overall current is in the same direction on both sides of the diode, as required.

The Shockley diode equation models the forward-bias operational characteristics of a p–n junction outside the avalanche (reverse-biased conducting) region.

Reverse bias

A silicon p–n junction in reverse bias

Connecting the p-type region to the negative terminal of the voltage supply and the n-type region to the positive terminal corresponds to reverse bias. If a diode is reverse-biased, the voltage at the cathode is comparatively higher than at the anode. Therefore, very little current flows until the diode breaks down. The connections are illustrated in the adjacent diagram.

Because the p-type material is now connected to the negative terminal of the power supply, the 'holes' in the p-type material are pulled away from the junction, leaving behind charged ions and causing the width of the depletion region to increase. Likewise, because the n-type region is connected to the positive terminal, the electrons are pulled away from the junction, with similar effect. This increases the voltage barrier causing a high resistance to the flow of charge carriers, thus allowing minimal electric current to cross the p–n junction. The increase in resistance of the p–n junction results in the junction behaving as an insulator.

The strength of the depletion zone electric field increases as the reverse-bias voltage increases. Once the electric field intensity increases beyond a critical level, the p–n junction depletion zone breaks down and current begins to flow, usually by either the Zener or the avalanche breakdown processes. Both of these breakdown processes are non-destructive and are reversible, as long as the amount of current flowing does not reach levels that cause the semiconductor material to overheat and cause thermal damage.

This effect is used to advantage in Zener diode regulator circuits. Zener diodes have a low breakdown voltage. A standard value for breakdown voltage is for instance 5.6 V. This means that the voltage at the cathode cannot be more than about 5.6 V higher than the voltage at the anode (though there is a slight rise with current), because the diode breaks down, and therefore conduct, if the voltage gets any higher. This, in effect, limits the voltage over the diode.

Another application of reverse biasing is Varactor diodes, where the width of the depletion zone (controlled with the reverse bias voltage) changes the capacitance of the diode.

Governing equations

Size of depletion region

See also: Band bending

For a p–n junction, let ${\displaystyle C_A(x)}$ be the concentration of negatively-charged acceptor atoms and ${\displaystyle C_D(x)}$ be the concentrations of positively-charged donor atoms. Let ${\displaystyle N_0(x)}$ and ${\displaystyle P_0(x)}$ be the equilibrium concentrations of electrons and holes respectively. Thus, by Poisson's equation:

$${\displaystyle -\frac{{\mathrm{d}}^{2}V}{\mathrm{d}{x}^2}=\frac{\rho }{\epsilon }=\frac{q}{\epsilon }\left[(P_0-N_0)+(C_D-C_A)\right]}$$

where ${\displaystyle V}$ is the electric potential, ${\displaystyle \rho }$ is the charge density, ${\displaystyle \epsilon }$ is permittivity and ${\displaystyle q}$ is the magnitude of the electron charge.

For a general case, the dopants have a concentration profile that varies with depth x, but for a simple case of an abrupt junction, ${\displaystyle C_A}$ can be assumed to be constant on the p side of the junction and zero on the n side, and ${\displaystyle C_D}$ can be assumed to be constant on the n side of the junction and zero on the p side. Let ${\displaystyle d_p}$ be the width of the depletion region on the p-side and ${\displaystyle d_n}$ the width of the depletion region on the n-side. Then, since ${\displaystyle P_0=N_0=0}$ within the depletion region, it must be that

$${\displaystyle d_p{C}_A=d_n{C}_D}$$

because the total charge on the p and the n side of the depletion region sums to zero. Therefore, letting ${\displaystyle D}$ and ${\displaystyle \mathrm{\Delta }V}$ represent the entire depletion region and the potential difference across it,

$${\displaystyle \mathrm{\Delta }V={\int }_D\int \frac{q}{\epsilon }\left[(P_0-N_0)+(C_D-C_A)\right]\mathrm{d}x\mathrm{d}x=\frac{C_A{C}_D}{C_A+C_D}\frac{q}{2\epsilon }(d_p+d_n{)}^2}$$

And thus, letting ${\displaystyle d}$ be the total width of the depletion region, we get

$${\displaystyle d=\sqrt{\frac{2\epsilon }{q}\frac{C_A+C_D}{C_A{C}_D}\mathrm{\Delta }V}}$$

${\displaystyle \mathrm{\Delta }V}$ can be written as ${\displaystyle \mathrm{\Delta }{V}_0+\mathrm{\Delta }{V}_{\text{ext}}}$, where we have broken up the voltage difference into the equilibrium plus external components. The equilibrium potential results from diffusion forces, and thus we can calculate ${\displaystyle \mathrm{\Delta }{V}_0}$ by implementing the Einstein relation and assuming the semiconductor is nondegenerate (i.e., the product ${\displaystyle P_0{N}_0=n_i^2}$ is independent of the Fermi energy):

$${\displaystyle \mathrm{\Delta }{V}_0=\frac{kT}{q}\ln \left(\frac{C_A{C}_D}{P_0{N}_0}\right)=\frac{kT}{q}\ln \left(\frac{C_A{C}_D}{n_i^2}\right)}$$

where T is the temperature of the semiconductor and k is Boltzmann constant.

Current across depletion region

The Shockley ideal diode equation characterizes the current across a p–n junction as a function of external voltage and ambient conditions (temperature, choice of semiconductor, etc.). To see how it can be derived, we must examine the various reasons for current. The convention is that the forward (+) direction be pointed against the diode's built-in potential gradient at equilibrium.

• Forward current (${\displaystyle {\mathbf{J}}_F}$)
  • Diffusion current: current due to local imbalances in carrier concentration ${\displaystyle n}$, via the equation ${\displaystyle {\mathbf{J}}_D\propto -q\mathrm{\nabla }n}$
• Reverse current (${\displaystyle {\mathbf{J}}_R}$)
  • Field current
  • Generation current

Doping (semiconductor)

From Wikipedia, the free encyclopedia

In semiconductor production, doping is the intentional introduction of impurities into an intrinsic semiconductor for the purpose of modulating its electrical, optical and structural properties. The doped material is referred to as an extrinsic semiconductor.

Small numbers of dopant atoms can change the ability of a semiconductor to conduct electricity. When on the order of one dopant atom is added per 100 million atoms, the doping is said to be low or light. When many more dopant atoms are added, on the order of one per ten thousand atoms, the doping is referred to as high or heavy. This is often shown as n+ for n-type doping or p+ for p-type doping. (See the article on semiconductors for a more detailed description of the doping mechanism.) A semiconductor doped to such high levels that it acts more like a conductor than a semiconductor is referred to as a degenerate semiconductor. A semiconductor can be considered i-type semiconductor if it has been doped in equal quantities of p and n.

In the context of phosphors and scintillators, doping is better known as activation; this is not to be confused with dopant activation in semiconductors. Doping is also used to control the color in some pigments.

History

The effects of impurities in semiconductors (doping) were long known empirically in such devices as crystal radio detectors and selenium rectifiers. For instance, in 1885 Shelford Bidwell, and in 1930 the German scientist Bernhard Gudden, each independently reported that the properties of semiconductors were due to the impurities they contained. A doping process was formally developed by John Robert Woodyard working at Sperry Gyroscope Company during World War II. Though the word doping is not used in it, his US Patent issued in 1950 describes methods for adding tiny amounts of solid elements from the nitrogen column of the periodic table to germanium to produce rectifying devices. The demands of his work on radar prevented Woodyard from pursuing further research on semiconductor doping.

Similar work was performed at Bell Labs by Gordon K. Teal and Morgan Sparks, with a US Patent issued in 1953.

Woodyard's prior patent proved to be the grounds of extensive litigation by Sperry Rand.

Carrier concentration

The concentration of the dopant used affects many electrical properties. Most important is the material's charge carrier concentration. In an intrinsic semiconductor under thermal equilibrium, the concentrations of electrons and holes are equivalent. That is,

${\displaystyle n=p=n_i.}$

In a non-intrinsic semiconductor under thermal equilibrium, the relation becomes (for low doping):

${\displaystyle n_0\cdot p_0=n_i^2}$

where n₀ is the concentration of conducting electrons, p₀ is the conducting hole concentration, and n_i is the material's intrinsic carrier concentration. The intrinsic carrier concentration varies between materials and is dependent on temperature. Silicon's n_i, for example, is roughly 1.08×10¹⁰ cm⁻³ at 300 kelvins, about room temperature.

In general, increased doping leads to increased conductivity due to the higher concentration of carriers. Degenerate (very highly doped) semiconductors have conductivity levels comparable to metals and are often used in integrated circuits as a replacement for metal. Often superscript plus and minus symbols are used to denote relative doping concentration in semiconductors. For example, n⁺ denotes an n-type semiconductor with a high, often degenerate, doping concentration. Similarly, p⁻ would indicate a very lightly doped p-type material. Even degenerate levels of doping imply low concentrations of impurities with respect to the base semiconductor. In intrinsic crystalline silicon, there are approximately 5×10²² atoms/cm³. Doping concentration for silicon semiconductors may range anywhere from 10¹³ cm⁻³ to 10¹⁸ cm⁻³. Doping concentration above about 10¹⁸ cm⁻³ is considered degenerate at room temperature. Degenerately doped silicon contains a proportion of impurity to silicon on the order of parts per thousand. This proportion may be reduced to parts per billion in very lightly doped silicon. Typical concentration values fall somewhere in this range and are tailored to produce the desired properties in the device that the semiconductor is intended for.

Effect on band structure

Band diagram of PN junction operation in forward bias mode showing reducing depletion width. Both p and n junctions are doped at a 1×10¹⁵/cm³ doping level, leading to built-in potential of ~0.59 V. Reducing depletion width can be inferred from the shrinking charge profile, as fewer dopants are exposed with increasing forward bias.

Doping a semiconductor in a good crystal introduces allowed energy states within the band gap, but very close to the energy band that corresponds to the dopant type. In other words, electron donor impurities create states near the conduction band while electron acceptor impurities create states near the valence band. The gap between these energy states and the nearest energy band is usually referred to as dopant-site bonding energy or E_B and is relatively small. For example, the E_B for boron in silicon bulk is 0.045 eV, compared with silicon's band gap of about 1.12 eV. Because E_B is so small, room temperature is hot enough to thermally ionize practically all of the dopant atoms and create free charge carriers in the conduction or valence bands.

Dopants also have the important effect of shifting the energy bands relative to the Fermi level. The energy band that corresponds with the dopant with the greatest concentration ends up closer to the Fermi level. Since the Fermi level must remain constant in a system in thermodynamic equilibrium, stacking layers of materials with different properties leads to many useful electrical properties induced by band bending, if the interfaces can be made cleanly enough. For example, the p-n junction's properties are due to the band bending that happens as a result of the necessity to line up the bands in contacting regions of p-type and n-type material. This effect is shown in a band diagram. The band diagram typically indicates the variation in the valence band and conduction band edges versus some spatial dimension, often denoted x. The Fermi level is also usually indicated in the diagram. Sometimes the intrinsic Fermi level, E_i, which is the Fermi level in the absence of doping, is shown. These diagrams are useful in explaining the operation of many kinds of semiconductor devices.

Relationship to carrier concentration (low doping)

For low levels of doping, the relevant energy states are populated sparsely by electrons (conduction band) or holes (valence band). It is possible to write simple expressions for the electron and hole carrier concentrations, by ignoring Pauli exclusion (via Maxwell–Boltzmann statistics):

${\displaystyle n_e=N_{\mathrm{C}}(T)\exp ((E_{\mathrm{F}}-E_{\mathrm{C}})/kT),n_h=N_{\mathrm{V}}(T)\exp ((E_{\mathrm{V}}-E_{\mathrm{F}})/kT),}$

where E_F is the Fermi level, E_C is the minimum energy of the conduction band, and E_V is the maximum energy of the valence band. These are related to the value of the intrinsic concentration via

${\displaystyle n_i^2=n_h{n}_e=N_{\mathrm{V}}(T)N_{\mathrm{C}}(T)\exp ((E_{\mathrm{V}}-E_{\mathrm{C}})/kT),}$

an expression which is independent of the doping level, since E_C – E_V (the band gap) does not change with doping.

The concentration factors N_C(T) and N_V(T) are given by

${\displaystyle N_{\mathrm{C}}(T)=2(2\pi m_e^{\ast }kT/h^2{)}^{3/2}{N}_{\mathrm{V}}(T)=2(2\pi m_h^{\ast }kT/h^2{)}^{3/2}.}$

where m_e^* and m_h^* are the density of states effective masses of electrons and holes, respectively, quantities that are roughly constant over temperature.

Techniques of doping and synthesis

Doping during crystal growth

Some dopants are added as the (usually silicon) boule is grown by Czochralski method, giving each wafer an almost uniform initial doping.

Alternately, synthesis of semiconductor devices may involve the use of vapor-phase epitaxy. In vapor-phase epitaxy, a gas containing the dopant precursor can be introduced into the reactor. For example, in the case of n-type gas doping of gallium arsenide, hydrogen sulfide is added, and sulfur is incorporated into the structure. This process is characterized by a constant concentration of sulfur on the surface. In the case of semiconductors in general, only a very thin layer of the wafer needs to be doped in order to obtain the desired electronic properties.

Post-growth doping

To define circuit elements, selected areas — typically controlled by photolithography — are further doped by such processes as diffusion and ion implantation, the latter method being more popular in large production runs because of increased controllability.

Spin-on glass

Spin-on glass or spin-on dopant doping is a two-step process of applying a mixture of SiO₂ and dopants (in a solvent) onto a wafer surface by spin-coating and then stripping it and baking it at a certain temperatue in the furnace at constant nitrogen+oxygen flow.

Neutron transmutation doping

See also: Neutron activation

Neutron transmutation doping (NTD) is an unusual doping method for special applications. Most commonly, it is used to dope silicon n-type in high-power electronics and semiconductor detectors. It is based on the conversion of the Si-30 isotope into phosphorus atom by neutron absorption as follows:

$${\displaystyle {}^{30}\mathrm{S}\mathrm{i}(n,\gamma ){}^{31}\mathrm{S}\mathrm{i}\to {}^{31}\mathrm{P}+{\beta }^{-}(T_{1/2}=2.62\mathrm{h}).}$$

In practice, the silicon is typically placed near a nuclear reactor to receive the neutrons. As neutrons continue to pass through the silicon, more and more phosphorus atoms are produced by transmutation, and therefore the doping becomes more and more strongly n-type. NTD is a far less common doping method than diffusion or ion implantation, but it has the advantage of creating an extremely uniform dopant distribution.

Dopant elements

Group IV semiconductors

(Note: When discussing periodic table groups, semiconductor physicists always use an older notation, not the current IUPAC group notation. For example, the carbon group is called "Group IV", not "Group 14".)

For the Group IV semiconductors such as diamond, silicon, germanium, silicon carbide, and silicon–germanium, the most common dopants are acceptors from Group III or donors from Group V elements. Boron, arsenic, phosphorus, and occasionally gallium are used to dope silicon. Boron is the p-type dopant of choice for silicon integrated circuit production because it diffuses at a rate that makes junction depths easily controllable. Phosphorus is typically used for bulk-doping of silicon wafers, while arsenic is used to diffuse junctions, because it diffuses more slowly than phosphorus and is thus more controllable.

By doping pure silicon with Group V elements such as phosphorus, extra valence electrons are added that become unbounded from individual atoms and allow the compound to be an electrically conductive n-type semiconductor. Doping with Group III elements, which are missing the fourth valence electron, creates "broken bonds" (holes) in the silicon lattice that are free to move. The result is an electrically conductive p-type semiconductor. In this context, a Group V element is said to behave as an electron donor, and a Group III element as an acceptor. This is a key concept in the physics of a diode.

A very heavily doped semiconductor behaves more like a good conductor (metal) and thus exhibits more linear positive thermal coefficient. Such effect is used for instance in sensistors. Lower dosage of doping is used in other types (NTC or PTC) thermistors.

Silicon dopants

• Acceptors, p-type
  • Boron is a p-type dopant. Its diffusion rate allows easy control of junction depths. Common in CMOS technology. Can be added by diffusion of diborane gas. The only acceptor with sufficient solubility for efficient emitters in transistors and other applications requiring extremely high dopant concentrations. Boron diffuses about as fast as phosphorus.
  • Aluminum, used for deep p-diffusions. Not popular in VLSI and ULSI. Also a common unintentional impurity.
  • Gallium is a dopant used for long-wavelength infrared photoconduction silicon detectors in the 8–14 μm atmospheric window. Gallium-doped silicon is also promising for solar cells, due to its long minority carrier lifetime with no lifetime degradation; as such it is gaining importance as a replacement of boron doped substrates for solar cell applications.
  • Indium is a dopant used for long-wavelength infrared photoconduction silicon detectors in the 3–5 μm atmospheric window.
• Donors, n-type
  • Phosphorus is a n-type dopant. It diffuses fast, so is usually used for bulk doping, or for well formation. Used in solar cells. Can be added by diffusion of phosphine gas. Bulk doping can be achieved by nuclear transmutation, by irradiation of pure silicon with neutrons in a nuclear reactor. Phosphorus also traps gold atoms, which otherwise quickly diffuse through silicon and act as recombination centers.
  • Arsenic is a n-type dopant. Its slower diffusion allows using it for diffused junctions. Used for buried layers. Has similar atomic radius to silicon, high concentrations can be achieved. Its diffusivity is about a tenth of phosphorus or boron, so it is used where the dopant should stay in place during subsequent thermal processing. Useful for shallow diffusions where well-controlled abrupt boundary is desired. Preferred dopant in VLSI circuits. Preferred dopant in low resistivity ranges.
  • Antimony is a n-type dopant. It has a small diffusion coefficient. Used for buried layers. Has diffusivity similar to arsenic, is used as its alternative. Its diffusion is virtually purely substitutional, with no interstitials, so it is free of anomalous effects. For this superior property, it is sometimes used in VLSI instead of arsenic. Heavy doping with antimony is important for power devices. Heavily antimony-doped silicon has lower concentration of oxygen impurities; minimal autodoping effects make it suitable for epitaxial substrates.
  • Bismuth is a promising dopant for long-wavelength infrared photoconduction silicon detectors, a viable n-type alternative to the p-type gallium-doped material.
  • Lithium is used for doping silicon for radiation hardened solar cells. The lithium presence anneals defects in the lattice produced by protons and neutrons. Lithium can be introduced to boron-doped p+ silicon, in amounts low enough to maintain the p character of the material, or in large enough amount to counterdope it to low-resistivity n type.
• Other
  • Germanium can be used for band gap engineering. Germanium layer also inhibits diffusion of boron during the annealing steps, allowing ultrashallow p-MOSFET junctions. Germanium bulk doping suppresses large void defects, increases internal gettering, and improves wafer mechanical strength.
  • Silicon, germanium and xenon can be used as ion beams for pre-amorphization of silicon wafer surfaces. Formation of an amorphous layer beneath the surface allows forming ultrashallow junctions for p-MOSFETs.
  • Nitrogen is important for growing defect-free silicon crystal. Improves mechanical strength of the lattice, increases bulk microdefect generation, suppresses vacancy agglomeration.
  • Gold and platinum are used for minority carrier lifetime control. They are used in some infrared detection applications. Gold introduces a donor level 0.35 eV above the valence band and an acceptor level 0.54 eV below the conduction band. Platinum introduces a donor level also at 0.35 eV above the valence band, but its acceptor level is only 0.26 eV below conduction band; as the acceptor level in n-type silicon is shallower, the space charge generation rate is lower and therefore the leakage current is also lower than for gold doping. At high injection levels platinum performs better for lifetime reduction. Reverse recovery of bipolar devices is more dependent on the low-level lifetime, and its reduction is better performed by gold. Gold provides a good tradeoff between forward voltage drop and reverse recovery time for fast switching bipolar devices, where charge stored in base and collector regions must be minimized. Conversely, in many power transistors a long minority carrier lifetime is required to achieve good gain, and the gold/platinum impurities must be kept low.

Other semiconductors

In the following list the "(substituting X)" refers to all of the materials preceding said parenthesis.

• Gallium arsenide
  • n-type: tellurium, sulfur (substituting As); tin, silicon, germanium (substituting Ga)
  • p-type: beryllium, zinc, chromium (substituting Ga); silicon, germanium, carbon (substituting As)
• Gallium phosphide
  • n-type: tellurium, selenium, sulfur (substituting phosphorus)
  • p-type: zinc, magnesium (substituting Ga); tin (substituting P)
  • isoelectric: nitrogen (substituting P) is added to enable luminescence in older green LEDs (GaP has indirect band gap)
• Gallium nitride, Indium gallium nitride, Aluminium gallium nitride
  • n-type: silicon (substituting Ga), germanium (substituting Ga, better lattice match), carbon (substituting Ga, naturally embedding into MOVPE-grown layers in low concentration)
  • p-type: magnesium (substituting Ga) - challenging due to relatively high ionisation energy above the valence band edge, strong diffusion of interstitial Mg, hydrogen complexes passivating of Mg acceptors and by Mg self-compensation at higher concentrations)
• Cadmium telluride
  • n-type: indium, aluminium (substituting Cd); chlorine (substituting Te)
  • p-type: phosphorus (substituting Te); lithium, sodium (substituting Cd)
• Cadmium sulfide
  • n-type: gallium (substituting Cd); iodine, fluorine (substituting S)
  • p-type: lithium, sodium (substituting Cd)

Compensation

In most cases many types of impurities will be present in the resultant doped semiconductor. If an equal number of donors and acceptors are present in the semiconductor, the extra core electrons provided by the former will be used to satisfy the broken bonds due to the latter, so that doping produces no free carriers of either type. This phenomenon is known as compensation, and occurs at the p-n junction in the vast majority of semiconductor devices.

Partial compensation, where donors outnumber acceptors or vice versa, allows device makers to repeatedly reverse (invert) the type of a certain layer under the surface of a bulk semiconductor by diffusing or implanting successively higher doses of dopants, so-called counterdoping. Most modern semiconductor devices are made by successive selective counterdoping steps to create the necessary P and N type areas under the surface of bulk silicon. This is an alternative to successively growing such layers by epitaxy.

Although compensation can be used to increase or decrease the number of donors or acceptors, the electron and hole mobility is always decreased by compensation because mobility is affected by the sum of the donor and acceptor ions.

Doping in conductive polymers

Main article: Conductive polymer

Conductive polymers can be doped by adding chemical reactants to oxidize, or sometimes reduce, the system so that electrons are pushed into the conducting orbitals within the already potentially conducting system. There are two primary methods of doping a conductive polymer, both of which use an oxidation-reduction (i.e., redox) process.

1. Chemical doping involves exposing a polymer such as melanin, typically a thin film, to an oxidant such as iodine or bromine. Alternatively, the polymer can be exposed to a reductant; this method is far less common, and typically involves alkali metals.
2. Electrochemical doping involves suspending a polymer-coated, working electrode in an electrolyte solution in which the polymer is insoluble along with separate counter and reference electrodes. An electric potential difference is created between the electrodes that causes a charge and the appropriate counter ion from the electrolyte to enter the polymer in the form of electron addition (i.e., n-doping) or removal (i.e., p-doping).

N-doping is much less common because the Earth's atmosphere is oxygen-rich, thus creating an oxidizing environment. An electron-rich, n-doped polymer will react immediately with elemental oxygen to de-dope (i.e., reoxidize to the neutral state) the polymer. Thus, chemical n-doping must be performed in an environment of inert gas (e.g., argon). Electrochemical n-doping is far more common in research, because it is easier to exclude oxygen from a solvent in a sealed flask. However, it is unlikely that n-doped conductive polymers are available commercially.

Doping in organic molecular semiconductors

Molecular dopants are preferred in doping molecular semiconductors due to their compatibilities of processing with the host, that is, similar evaporation temperatures or controllable solubility. Additionally, the relatively large sizes of molecular dopants compared with those of metal ion dopants (such as Li⁺ and Mo⁶⁺) are generally beneficial, yielding excellent spatial confinement for use in multilayer structures, such as OLEDs and Organic solar cells. Typical p-type dopants include F4-TCNQ and Mo(tfd)₃. However, similar to the problem encountered in doping conductive polymers, air-stable n-dopants suitable for materials with low electron affinity (EA) are still elusive. Recently, photoactivation with a combination of cleavable dimeric dopants, such as [RuCp^∗Mes]₂, suggests a new path to realize effective n-doping in low-EA materials.

Magnetic doping

Main article: Magnetic semiconductor

Research on magnetic doping has shown that considerable alteration of certain properties such as specific heat may be affected by small concentrations of an impurity; for example, dopant impurities in semiconducting ferromagnetic alloys can generate different properties as first predicted by White, Hogan, Suhl and Nakamura. The inclusion of dopant elements to impart dilute magnetism is of growing significance in the field of Magnetic semiconductors. The presence of disperse ferromagnetic species is key to the functionality of emerging Spintronics, a class of systems that utilise electron spin in addition to charge. Using Density functional theory (DFT) the temperature dependent magnetic behaviour of dopants within a given lattice can be modeled to identify candidate semiconductor systems.

Single dopants in semiconductors

The sensitive dependence of a semiconductor's properties on dopants has provided an extensive range of tunable phenomena to explore and apply to devices. It is possible to identify the effects of a solitary dopant on commercial device performance as well as on the fundamental properties of a semiconductor material. New applications have become available that require the discrete character of a single dopant, such as single-spin devices in the area of quantum information or single-dopant transistors. Dramatic advances in the past decade towards observing, controllably creating and manipulating single dopants, as well as their application in novel devices have allowed opening the new field of solotronics (solitary dopant optoelectronics).

Modulation doping

Electrons or holes introduced by doping are mobile, and can be spatially separated from dopant atoms they have dissociated from. Ionized donors and acceptors however attract electrons and holes, respectively, so this spatial separation requires abrupt changes of dopant levels, of band gap (e.g. a quantum well), or built-in electric fields (e.g. in case of noncentrosymmetric crystals). This technique is called modulation doping and is advantageous owing to suppressed carrier-donor scattering, allowing very high mobility to be attained.

Fermi liquid theory

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Fermi_liquid_theory

Fermi liquid theory (also known as Landau's Fermi-liquid theory) is a theoretical model of interacting fermions that describes the normal state of most metals at sufficiently low temperatures. The interactions among the particles of the many-body system do not need to be small. The phenomenological theory of Fermi liquids was introduced by the Soviet physicist Lev Davidovich Landau in 1956, and later developed by Alexei Abrikosov and Isaak Khalatnikov using diagrammatic perturbation theory. The theory explains why some of the properties of an interacting fermion system are very similar to those of the ideal Fermi gas (i.e. non-interacting fermions), and why other properties differ.

Important examples of where Fermi liquid theory has been successfully applied are most notably electrons in most metals and liquid helium-3. Liquid helium-3 is a Fermi liquid at low temperatures (but not low enough to be in its superfluid phase). Helium-3 is an isotope of helium, with 2 protons, 1 neutron and 2 electrons per atom. Because there is an odd number of fermions inside the nucleus, the atom itself is also a fermion. The electrons in a normal (non-superconducting) metal also form a Fermi liquid, as do the nucleons (protons and neutrons) in an atomic nucleus. Strontium ruthenate displays some key properties of Fermi liquids, despite being a strongly correlated material, and is compared with high temperature superconductors like cuprates. More dramatic examples are metallic rare-earth alloys with partially filled f-orbitals which at very low temperature are described as Fermi liquids. The electrons in these Fermi liquids have masses that are strongly enhanced by their interactions with other electrons, and hence these systems are known as heavy Fermi liquids.

Description

The key ideas behind Landau's theory are the notion of adiabaticity and the Pauli exclusion principle. Consider a non-interacting fermion system (a Fermi gas), and suppose we "turn on" the interaction slowly. Landau argued that in this situation, the ground state of the Fermi gas would adiabatically transform into the ground state of the interacting system.

By Pauli's exclusion principle, the ground state ${\displaystyle {\mathrm{\Psi }}_0}$ of a Fermi gas consists of fermions occupying all momentum states corresponding to momentum ${\displaystyle p<p_{\mathrm{F}}}$ with all higher momentum states unoccupied. As the interaction is turned on, the spin, charge and momentum of the fermions corresponding to the occupied states remain unchanged, while their dynamical properties, such as their mass, magnetic moment etc. are renormalized to new values. Thus, there is a one-to-one correspondence between the elementary excitations of a Fermi gas system and a Fermi liquid system. In the context of Fermi liquids, these excitations are called "quasi-particles".

Landau quasiparticles are long-lived excitations with a lifetime ${\displaystyle \tau }$ that satisfies ${\displaystyle \frac{\hslash }{\tau }\ll {ϵ}_{\mathrm{p}}}$ where ${\displaystyle {ϵ}_{\mathrm{p}}}$ is the quasiparticle energy (measured from the Fermi energy). At finite temperature, ${\displaystyle {ϵ}_{\mathrm{p}}}$ is on the order of the thermal energy ${\displaystyle k_{\mathrm{B}}T}$, and the condition for Landau quasiparticles can be reformulated as ${\displaystyle \frac{\hslash }{\tau }\ll k_{\mathrm{B}}T}$.

For this system, the Green's function can be written (near its poles) in the form

${\displaystyle G(\omega ,p)\approx \frac{Z}{\omega +\mu -ϵ(p)}}$

where ${\displaystyle \mu }$ is the chemical potential and ${\displaystyle ϵ(p)}$ is the energy corresponding to the given momentum state.

The value ${\displaystyle Z}$ is called the quasiparticle residue and is very characteristic of Fermi liquid theory. The spectral function for the system can be directly observed via angle-resolved photoemission spectroscopy (ARPES), and can be written (in the limit of low-lying excitations) in the form:

${\displaystyle A(\mathbf{k},\omega )=Z\delta (\omega -v_{\mathrm{F}}{k}_{\Vert })}$

where ${\displaystyle v_{\mathrm{F}}}$ is the Fermi velocity.

Physically, we can say that a propagating fermion interacts with its surrounding in such a way that the net effect of the interactions is to make the fermion behave as a "dressed" fermion, altering its effective mass and other dynamical properties. These "dressed" fermions are what we think of as "quasiparticles".

Another important property of Fermi liquids is related to the scattering cross section for electrons. Suppose we have an electron with energy ${\displaystyle {ϵ}_1}$ above the Fermi surface, and suppose it scatters with a particle in the Fermi sea with energy ${\displaystyle {ϵ}_2}$. By Pauli's exclusion principle, both the particles after scattering have to lie above the Fermi surface, with energies ${\displaystyle {ϵ}_3,{ϵ}_4>{ϵ}_{\mathrm{F}}}$. Now, suppose the initial electron has energy very close to the Fermi surface ${\displaystyle ϵ\approx {ϵ}_{\mathrm{F}}}$ Then, we have that ${\displaystyle {ϵ}_2,{ϵ}_3,{ϵ}_4}$ also have to be very close to the Fermi surface. This reduces the phase space volume of the possible states after scattering, and hence, by Fermi's golden rule, the scattering cross section goes to zero. Thus we can say that the lifetime of particles at the Fermi surface goes to infinity.

Similarities to Fermi gas

The Fermi liquid is qualitatively analogous to the non-interacting Fermi gas, in the following sense: The system's dynamics and thermodynamics at low excitation energies and temperatures may be described by substituting the non-interacting fermions with interacting quasiparticles, each of which carries the same spin, charge and momentum as the original particles. Physically these may be thought of as being particles whose motion is disturbed by the surrounding particles and which themselves perturb the particles in their vicinity. Each many-particle excited state of the interacting system may be described by listing all occupied momentum states, just as in the non-interacting system. As a consequence, quantities such as the heat capacity of the Fermi liquid behave qualitatively in the same way as in the Fermi gas (e.g. the heat capacity rises linearly with temperature).

Differences from Fermi gas

The following differences to the non-interacting Fermi gas arise:

Energy

The energy of a many-particle state is not simply a sum of the single-particle energies of all occupied states. Instead, the change in energy for a given change ${\displaystyle \delta n_k}$ in occupation of states ${\displaystyle k}$ contains terms both linear and quadratic in ${\displaystyle \delta n_k}$ (for the Fermi gas, it would only be linear, ${\displaystyle \delta n_k{ϵ}_k}$, where ${\displaystyle {ϵ}_k}$ denotes the single-particle energies). The linear contribution corresponds to renormalized single-particle energies, which involve, e.g., a change in the effective mass of particles. The quadratic terms correspond to a sort of "mean-field" interaction between quasiparticles, which is parametrized by so-called Landau Fermi liquid parameters and determines the behaviour of density oscillations (and spin-density oscillations) in the Fermi liquid. Still, these mean-field interactions do not lead to a scattering of quasi-particles with a transfer of particles between different momentum states.

The renormalization of the mass of a fluid of interacting fermions can be calculated from first principles using many-body computational techniques. For the two-dimensional homogeneous electron gas, GW calculations and quantum Monte Carlo methods have been used to calculate renormalized quasiparticle effective masses.

Specific heat and compressibility

Specific heat, compressibility, spin-susceptibility and other quantities show the same qualitative behaviour (e.g. dependence on temperature) as in the Fermi gas, but the magnitude is (sometimes strongly) changed.

Interactions

In addition to the mean-field interactions, some weak interactions between quasiparticles remain, which lead to scattering of quasiparticles off each other. Therefore, quasiparticles acquire a finite lifetime. However, at low enough energies above the Fermi surface, this lifetime becomes very long, such that the product of excitation energy (expressed in frequency) and lifetime is much larger than one. In this sense, the quasiparticle energy is still well-defined (in the opposite limit, Heisenberg's uncertainty relation would prevent an accurate definition of the energy).

Structure

The structure of the "bare" particles (as opposed to quasiparticle) Green's function is similar to that in the Fermi gas (where, for a given momentum, the Green's function in frequency space is a delta peak at the respective single-particle energy). The delta peak in the density-of-states is broadened (with a width given by the quasiparticle lifetime). In addition (and in contrast to the quasiparticle Green's function), its weight (integral over frequency) is suppressed by a quasiparticle weight factor ${\displaystyle 0<Z<1}$. The remainder of the total weight is in a broad "incoherent background", corresponding to the strong effects of interactions on the fermions at short time-scales.

Distribution

The distribution of particles (as opposed to quasiparticles) over momentum states at zero temperature still shows a discontinuous jump at the Fermi surface (as in the Fermi gas), but it does not drop from 1 to 0: the step is only of size ${\displaystyle Z}$.

Electrical resistivity

In a metal the resistivity at low temperatures is dominated by electron-electron scattering in combination with umklapp scattering. For a Fermi liquid, the resistivity from this mechanism varies as ${\displaystyle T^2}$, which is often taken as an experimental check for Fermi liquid behaviour (in addition to the linear temperature-dependence of the specific heat), although it only arises in combination with the lattice. In certain cases, umklapp scattering is not required. For example, the resistivity of compensated semimetals scales as ${\displaystyle T^2}$ because of mutual scattering of electron and hole. This is known as the Baber mechanism.

Optical response

Fermi liquid theory predicts that the scattering rate, which governs the optical response of metals, not only depends quadratically on temperature (thus causing the ${\displaystyle T^2}$ dependence of the DC resistance), but it also depends quadratically on frequency. This is in contrast to the Drude prediction for non-interacting metallic electrons, where the scattering rate is a constant as a function of frequency. One material in which optical Fermi liquid behavior was experimentally observed is the low-temperature metallic phase of Sr₂RuO₄.

Instabilities

The experimental observation of exotic phases in strongly correlated systems has triggered an enormous effort from the theoretical community to try to understand their microscopic origin. One possible route to detect instabilities of a Fermi liquid is precisely the analysis done by Isaak Pomeranchuk. Due to that, the Pomeranchuk instability has been studied by several authors  with different techniques in the last few years and in particular, the instability of the Fermi liquid towards the nematic phase was investigated for several models.

Non-Fermi liquids

The term non-Fermi liquid, also known as "strange metal", is used to describe a system which displays breakdown of Fermi-liquid behaviour. The simplest example of such a system is the system of interacting fermions in one dimension, called the Luttinger liquid. Although Luttinger liquids are physically similar to Fermi liquids, the restriction to one dimension gives rise to several qualitative differences such as the absence of a quasiparticle peak in the momentum dependent spectral function, spin-charge separation, and the presence of spin density waves. One cannot ignore the existence of interactions in one-dimension and has to describe the problem with a non-Fermi theory, where Luttinger liquid is one of them. At small finite spin-temperatures in one-dimension the ground-state of the system is described by spin-incoherent Luttinger liquid (SILL).

Another example of such behaviour is observed at quantum critical points of certain second-order phase transitions, such as heavy fermion criticality, Mott criticality and high-${\displaystyle T_{\mathrm{c}}}$ cuprate phase transitions. The ground state of such transitions is characterized by the presence of a sharp Fermi surface, although there may not be well-defined quasiparticles. That is, on approaching the critical point, it is observed that the quasiparticle residue ${\displaystyle Z\to 0}$.

Understanding the behaviour of non-Fermi liquids is an important problem in condensed matter physics. Approaches towards explaining these phenomena include the treatment of marginal Fermi liquids; attempts to understand critical points and derive scaling relations; and descriptions using emergent gauge theories with techniques of holographic gauge/gravity duality.