Physical cosmology

From Wikipedia, the free encyclopedia

Physical cosmology is the study of the largest-scale structures and dynamics of the Universe and is concerned with fundamental questions about its origin, structure, evolution, and ultimate fate.^[1] Cosmology as a science originated with the Copernican principle, which implies that celestial bodies obey identical physical laws to those on Earth, and Newtonian mechanics, which first allowed us to understand those physical laws. Physical cosmology, as it is now understood, began with the development in 1915 of Albert Einstein's general theory of relativity, followed by major observational discoveries in the 1920s: first, Edwin Hubble discovered that the universe contains a huge number of external galaxies beyond our own Milky Way; then, work by Vesto Slipher and others showed that the universe is expanding. These advances made it possible to speculate about the origin of the universe, and allowed the establishment of the Big Bang Theory, by Georges Lemaître, as the leading cosmological model. A few researchers still advocate a handful of alternative cosmologies;^[2] however, most cosmologists agree that the Big Bang theory explains the observations better.

Dramatic advances in observational cosmology since the 1990s, including the cosmic microwave background, distant supernovae and galaxy redshift surveys, have led to the development of a standard model of cosmology. This model requires the universe to contain large amounts of dark matter and dark energy whose nature is currently not well understood, but the model gives detailed predictions that are in excellent agreement with many diverse observations.^[3]

Cosmology draws heavily on the work of many disparate areas of research in theoretical and applied physics. Areas relevant to cosmology include particle physics experiments and theory, theoretical and observational astrophysics, general relativity, quantum mechanics, and plasma physics.

Subject history

Modern cosmology developed along tandem tracks of theory and observation. In 1916, Albert Einstein published his theory of general relativity, which provided a unified description of gravity as a geometric property of space and time.^[4] At the time, Einstein believed in a static universe, but found that his original formulation of the theory did not permit it.^[5] This is because masses distributed throughout the universe gravitationally attract, and move toward each other over time.^[6] However, he realized that his equations permitted the introduction of a constant term which could counteract the attractive force of gravity on the cosmic scale. Einstein published his first paper on relativistic cosmology in 1917, in which he added this cosmological constant to his field equations in order to force them to model a static universe.^[7] The Einstein model describes a static universe; space is finite and unbounded (analogous to the surface of a sphere, which has a finite area but no edges). However, this so-called Einstein model is unstable to small perturbations—it will eventually start to expand or contract.^[5] It was later realized that Einstein's model was just one of a larger set of possibilities, all of which were consistent with general relativity and the cosmological principle. The cosmological solutions of general relativity were found by Alexander Friedmann in the early 1920s.^[8] His equations describe the Friedmann–Lemaître–Robertson–Walker universe, which may expand or contract, and whose geometry may be open, flat, or closed.

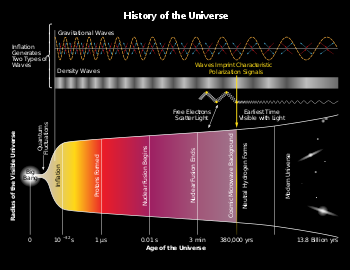
History of the Universe – gravitational waves are hypothesized to arise from cosmic inflation, a faster-than-light expansion just after the Big Bang^[9][10][11]

In the 1910s, Vesto Slipher (and later Carl Wilhelm Wirtz) interpreted the red shift of spiral nebulae as a Doppler shift that indicated they were receding from Earth.^[12][13] However, it is difficult to determine the distance to astronomical objects. One way is to compare the physical size of an object to its angular size, but a physical size must be assumed to do this. Another method is to measure the brightness of an object and assume an intrinsic luminosity, from which the distance may be determined using the inverse square law. Due to the difficulty of using these methods, they did not realize that the nebulae were actually galaxies outside our own Milky Way, nor did they speculate about the cosmological implications. In 1927, the Belgian Roman Catholic priest Georges Lemaître independently derived the Friedmann–Lemaître–Robertson–Walker equations and proposed, on the basis of the recession of spiral nebulae, that the universe began with the "explosion" of a "primeval atom"^[14]—which was later called the Big Bang. In 1929, Edwin Hubble provided an observational basis for Lemaître's theory. Hubble showed that the spiral nebulae were galaxies by determining their distances using measurements of the brightness of Cepheid variable stars. He discovered a relationship between the redshift of a galaxy and its distance. He interpreted this as evidence that the galaxies are receding from Earth in every direction at speeds proportional to their distance.^[15] This fact is now known as Hubble's law, though the numerical factor Hubble found relating recessional velocity and distance was off by a factor of ten, due to not knowing about the types of Cepheid variables.

Given the cosmological principle, Hubble's law suggested that the universe was expanding. Two primary explanations were proposed for the expansion. One was Lemaître's Big Bang theory, advocated and developed by George Gamow. The other explanation was Fred Hoyle's steady state model in which new matter is created as the galaxies move away from each other. In this model, the universe is roughly the same at any point in time.^[16][17]

For a number of years, support for these theories was evenly divided. However, the observational evidence began to support the idea that the universe evolved from a hot dense state. The discovery of the cosmic microwave background in 1965 lent strong support to the Big Bang model,^[17] and since the precise measurements of the cosmic microwave background by the Cosmic Background Explorer in the early 1990s, few cosmologists have seriously proposed other theories of the origin and evolution of the cosmos. One consequence of this is that in standard general relativity, the universe began with a singularity, as demonstrated by Roger Penrose and Stephen Hawking in the 1960s.^[18]

An alternative view to extend the Big Bang model, suggesting the universe had no beginning or singularity and the age of the universe is infinite, has been presented.^[19][20][21]

Energy of the cosmos

The lightest chemical elements, primarily hydrogen and helium, were created during the Big Bang through the process of nucleosynthesis.^[22] In a sequence of stellar nucleosynthesis reactions, smaller atomic nuclei are then combined into larger atomic nuclei, ultimately forming stable iron group elements such as iron and nickel, which have the highest nuclear binding energies.^[23] The net process results in a later energy release, meaning subsequent to the Big Bang.^[24] Such reactions of nuclear particles can lead to sudden energy releases from cataclysmic variables such as novae. Gravitational collapse of matter into black holes also powers the most energetic processes, generally seen in the nuclear regions of galaxies, forming quasars and active galaxies.

Cosmologists cannot explain all cosmic phenomena exactly, such as those related to the accelerating expansion of the universe, using conventional forms of energy. Instead, cosmologists propose a new form of energy called dark energy that permeates all space.^[25] One hypothesis is that dark energy is just the vacuum energy, a component of empty space that is associated with the virtual particles that exist due to the uncertainty principle.^[26]

There is no clear way to define the total energy in the universe using the most widely accepted theory of gravity, general relativity. Therefore, it remains controversial whether the total energy is conserved in an expanding universe. For instance, each photon that travels through intergalactic space loses energy due to the redshift effect. This energy is not obviously transferred to any other system, so seems to be permanently lost. On the other hand, some cosmologists insist that energy is conserved in some sense; this follows the law of conservation of energy.^[27]

Thermodynamics of the universe is a field of study that explores which form of energy dominates the cosmos – relativistic particles which are referred to as radiation, or non-relativistic particles referred to as matter. Relativistic particles are particles whose rest mass is zero or negligible compared to their kinetic energy, and so move at the speed of light or very close to it; non-relativistic particles have much higher rest mass than their energy and so move much slower than the speed of light.

As the universe expands, both matter and radiation in it become diluted. However, the energy densities of radiation and matter dilute at different rates. As a particular volume expands, mass energy density is changed only by the increase in volume, but the energy density of radiation is changed both by the increase in volume and by the increase in the wavelength of the photons that make it up. Thus the energy of radiation becomes a smaller part of the universe's total energy than that of matter as it expands. The very early universe is said to have been 'radiation dominated' and radiation controlled the deceleration of expansion. Later, as the average energy per photon becomes roughly 10 eV and lower, matter dictates the rate of deceleration and the universe is said to be 'matter dominated'. The intermediate case is not treated well analytically. As the expansion of the universe continues, matter dilutes even further and the cosmological constant becomes dominant, leading to an acceleration in the universe's expansion.

History of the universe

The history of the universe is a central issue in cosmology. The history of the universe is divided into different periods called epochs, according to the dominant forces and processes in each period. The standard cosmological model is known as the Lambda-CDM model.

Equations of motion

Within the standard cosmological model, the equations of motion governing the universe as a whole are derived from general relativity with a small, positive cosmological constant.^[28] The solution is an expanding universe; due to this expansion, the radiation and matter in the universe cool down and become diluted. At first, the expansion is slowed down by gravitation attracting the radiation and matter in the universe. However, as these become diluted, the cosmological constant becomes more dominant and the expansion of the universe starts to accelerate rather than decelerate. In our universe this happened billions of years ago.^[29]

Particle physics in cosmology

During the earliest moments of the universe the average energy density was very high, making knowledge of particle physics critical to understanding this environment. Hence, scattering processes and decay of unstable elementary particles are important for cosmological models of this period.
As a rule of thumb, a scattering or a decay process is cosmologically important in a certain epoch if the time scale describing that process is smaller than, or comparable to, the time scale of the expansion of the universe.^{[clarification needed]} The time scale that describes the expansion of the universe is ${\displaystyle 1/H}$ with ${\displaystyle H}$ being the Hubble parameter, which varies with time. The expansion timescale ${\displaystyle 1/H}$ is roughly equal to the age of the universe at each point in time.

Timeline of the Big Bang

Observations suggest that the universe began around 13.8 billion years ago.^[30] Since then, the evolution of the universe has passed through three phases. The very early universe, which is still poorly understood, was the split second in which the universe was so hot that particles had energies higher than those currently accessible in particle accelerators on Earth. Therefore, while the basic features of this epoch have been worked out in the Big Bang theory, the details are largely based on educated guesses. Following this, in the early universe, the evolution of the universe proceeded according to known high energy physics. This is when the first protons, electrons and neutrons formed, then nuclei and finally atoms. With the formation of neutral hydrogen, the cosmic microwave background was emitted. Finally, the epoch of structure formation began, when matter started to aggregate into the first stars and quasars, and ultimately galaxies, clusters of galaxies and superclusters formed. The future of the universe is not yet firmly known, but according to the ΛCDM model it will continue expanding forever.

Areas of study

Below, some of the most active areas of inquiry in cosmology are described, in roughly chronological order. This does not include all of the Big Bang cosmology, which is presented in Timeline of the Big Bang.

Very early universe

The early, hot universe appears to be well explained by the Big Bang from roughly 10⁻³³ seconds onwards, but there are several problems. One is that there is no compelling reason, using current particle physics, for the universe to be flat, homogeneous, and isotropic (see the cosmological principle). Moreover, grand unified theories of particle physics suggest that there should be magnetic monopoles in the universe, which have not been found. These problems are resolved by a brief period of cosmic inflation, which drives the universe to flatness, smooths out anisotropies and inhomogeneities to the observed level, and exponentially dilutes the monopoles.^[31] The physical model behind cosmic inflation is extremely simple, but it has not yet been confirmed by particle physics, and there are difficult problems reconciling inflation and quantum field theory. Some cosmologists think that string theory and brane cosmology will provide an alternative to inflation.^[32]

Another major problem in cosmology is what caused the universe to contain far more matter than antimatter. Cosmologists can observationally deduce that the universe is not split into regions of matter and antimatter. If it were, there would be X-rays and gamma rays produced as a result of annihilation, but this is not observed. Therefore, some process in the early universe must have created a small excess of matter over antimatter, and this (currently not understood) process is called baryogenesis. Three required conditions for baryogenesis were derived by Andrei Sakharov in 1967, and requires a violation of the particle physics symmetry, called CP-symmetry, between matter and antimatter.^[33] However, particle accelerators measure too small a violation of CP-symmetry to account for the baryon asymmetry. Cosmologists and particle physicists look for additional violations of the CP-symmetry in the early universe that might account for the baryon asymmetry.^[34]

Both the problems of baryogenesis and cosmic inflation are very closely related to particle physics, and their resolution might come from high energy theory and experiment, rather than through observations of the universe.^{[speculation?]}

Big Bang Theory

Big Bang nucleosynthesis is the theory of the formation of the elements in the early universe. It finished when the universe was about three minutes old and its temperature dropped below that at which nuclear fusion could occur. Big Bang nucleosynthesis had a brief period during which it could operate, so only the very lightest elements were produced. Starting from hydrogen ions (protons), it principally produced deuterium, helium-4, and lithium. Other elements were produced in only trace abundances. The basic theory of nucleosynthesis was developed in 1948 by George Gamow, Ralph Asher Alpher, and Robert Herman.^[35] It was used for many years as a probe of physics at the time of the Big Bang, as the theory of Big Bang nucleosynthesis connects the abundances of primordial light elements with the features of the early universe.^[22] Specifically, it can be used to test the equivalence principle,^[36] to probe dark matter, and test neutrino physics.^[37] Some cosmologists have proposed that Big Bang nucleosynthesis suggests there is a fourth "sterile" species of neutrino.^[38]

Standard model of Big Bang cosmology

The ΛCDM (Lambda cold dark matter) or Lambda-CDM model is a parametrization of the Big Bang cosmological model in which the universe contains a cosmological constant, denoted by Lambda (Greek Λ), associated with dark energy, and cold dark matter (abbreviated CDM). It is frequently referred to as the standard model of Big Bang cosmology.^[39][40]

Cosmic microwave background

Evidence of gravitational waves in the infant universe may have been uncovered by the microscopic examination of the focal plane of the BICEP2 radio telescope.^{[9][10][11][41]}

The cosmic microwave background is radiation left over from decoupling after the epoch of recombination when neutral atoms first formed. At this point, radiation produced in the Big Bang stopped Thomson scattering from charged ions. The radiation, first observed in 1965 by Arno Penzias and Robert Woodrow Wilson, has a perfect thermal black-body spectrum. It has a temperature of 2.7 kelvins today and is isotropic to one part in 10⁵. Cosmological perturbation theory, which describes the evolution of slight inhomogeneities in the early universe, has allowed cosmologists to precisely calculate the angular power spectrum of the radiation, and it has been measured by the recent satellite experiments (COBE and WMAP)^[42] and many ground and balloon-based experiments (such as Degree Angular Scale Interferometer, Cosmic Background Imager, and Boomerang).^[43] One of the goals of these efforts is to measure the basic parameters of the Lambda-CDM model with increasing accuracy, as well as to test the predictions of the Big Bang model and look for new physics. The results of measurements made by WMAP, for example, have placed limits on the neutrino masses.^[44]

Newer experiments, such as QUIET and the Atacama Cosmology Telescope, are trying to measure the polarization of the cosmic microwave background.^[45] These measurements are expected to provide further confirmation of the theory as well as information about cosmic inflation, and the so-called secondary anisotropies,^[46] such as the Sunyaev-Zel'dovich effect and Sachs-Wolfe effect, which are caused by interaction between galaxies and clusters with the cosmic microwave background.^[47][48]

On 17 March 2014, astronomers of the BICEP2 Collaboration announced the apparent detection of B-mode polarization of the CMB, considered to be evidence of primordial gravitational waves that are predicted by the theory of inflation to occur during the earliest phase of the Big Bang. However, later that year the Planck collaboration provided a more accurate measurement of cosmic dust, concluding that the B-mode signal from dust is the same strength as that reported from BICEP2.^[49][50] On January 30, 2015, a joint analysis of BICEP2 and Planck data was published and the European Space Agency announced that the signal can be entirely attributed to interstellar dust in the Milky Way.^[51]

Formation and evolution of large-scale structure

Understanding the formation and evolution of the largest and earliest structures (i.e., quasars, galaxies, clusters and superclusters) is one of the largest efforts in cosmology. Cosmologists study a model of hierarchical structure formation in which structures form from the bottom up, with smaller objects forming first, while the largest objects, such as superclusters, are still assembling.^[52] One way to study structure in the universe is to survey the visible galaxies, in order to construct a three-dimensional picture of the galaxies in the universe and measure the matter power spectrum. This is the approach of the Sloan Digital Sky Survey and the 2dF Galaxy Redshift Survey.^[53][54]

Another tool for understanding structure formation is simulations, which cosmologists use to study the gravitational aggregation of matter in the universe, as it clusters into filaments, superclusters and voids. Most simulations contain only non-baryonic cold dark matter, which should suffice to understand the universe on the largest scales, as there is much more dark matter in the universe than visible, baryonic matter. More advanced simulations are starting to include baryons and study the formation of individual galaxies. Cosmologists study these simulations to see if they agree with the galaxy surveys, and to understand any discrepancy.^[55]

Other, complementary observations to measure the distribution of matter in the distant universe and to probe reionization include:

• The Lyman-alpha forest, which allows cosmologists to measure the distribution of neutral atomic hydrogen gas in the early universe, by measuring the absorption of light from distant quasars by the gas.^[56]
• The 21 centimeter absorption line of neutral atomic hydrogen also provides a sensitive test of cosmology.^[57]
• Weak lensing, the distortion of a distant image by gravitational lensing due to dark matter.^[58]

These will help cosmologists settle the question of when and how structure formed in the universe.

Dark matter

Evidence from Big Bang nucleosynthesis, the cosmic microwave background, structure formation, and galaxy rotation curves suggests that about 23% of the mass of the universe consists of non-baryonic dark matter, whereas only 4% consists of visible, baryonic matter. The gravitational effects of dark matter are well understood, as it behaves like a cold, non-radiative fluid that forms haloes around galaxies. Dark matter has never been detected in the laboratory, and the particle physics nature of dark matter remains completely unknown. Without observational constraints, there are a number of candidates, such as a stable supersymmetric particle, a weakly interacting massive particle, a gravitationally-interacting massive particle, an axion, and a massive compact halo object. Alternatives to the dark matter hypothesis include a modification of gravity at small accelerations (MOND) or an effect from brane cosmology.^[59]

Dark energy

If the universe is flat, there must be an additional component making up 73% (in addition to the 23% dark matter and 4% baryons) of the energy density of the universe. This is called dark energy. In order not to interfere with Big Bang nucleosynthesis and the cosmic microwave background, it must not cluster in haloes like baryons and dark matter. There is strong observational evidence for dark energy, as the total energy density of the universe is known through constraints on the flatness of the universe, but the amount of clustering matter is tightly measured, and is much less than this. The case for dark energy was strengthened in 1999, when measurements demonstrated that the expansion of the universe has begun to gradually accelerate.^[60]

Apart from its density and its clustering properties, nothing is known about dark energy. Quantum field theory predicts a cosmological constant (CC) much like dark energy, but 120 orders of magnitude larger than that observed.^[61] Steven Weinberg and a number of string theorists (see string landscape) have invoked the 'weak anthropic principle': i.e. the reason that physicists observe a universe with such a small cosmological constant is that no physicists (or any life) could exist in a universe with a larger cosmological constant. Many cosmologists find this an unsatisfying explanation: perhaps because while the weak anthropic principle is self-evident (given that living observers exist, there must be at least one universe with a cosmological constant which allows for life to exist) it does not attempt to explain the context of that universe.^[62] For example, the weak anthropic principle alone does not distinguish between:

• Only one universe will ever exist and there is some underlying principle that constrains the CC to the value we observe.
• Only one universe will ever exist and although there is no underlying principle fixing the CC, we got lucky.
• Lots of universes exist (simultaneously or serially) with a range of CC values, and of course ours is one of the life-supporting ones.

Other possible explanations for dark energy include quintessence^[63] or a modification of gravity on the largest scales.^[64] The effect on cosmology of the dark energy that these models describe is given by the dark energy's equation of state, which varies depending upon the theory. The nature of dark energy is one of the most challenging problems in cosmology.

A better understanding of dark energy is likely to solve the problem of the ultimate fate of the universe. In the current cosmological epoch, the accelerated expansion due to dark energy is preventing structures larger than superclusters from forming. It is not known whether the acceleration will continue indefinitely, perhaps even increasing until a big rip, or whether it will eventually reverse, lead to a big freeze, or follow some other scenario.^[65]

Gravitational waves

Gravitational waves are ripples in the curvature of spacetime that propagate as waves at the speed of light, generated in certain gravitational interactions that propagate outward from their source.  Gravitational-wave astronomy is an emerging branch of observational astronomy which aims to use gravitational waves to collect observational data about sources of detectable gravitational waves such as binary star systems composed of white dwarfs, neutron stars, and black holes; and events such as supernovae, and the formation of the early universe shortly after the Big Bang.^[66]

In 2016, the LIGO Scientific Collaboration and Virgo Collaboration teams announced that they had made the first observation of gravitational waves, originating from a pair of merging black holes using the Advanced LIGO detectors.^[67][68][69] On June 15, 2016, a second detection of gravitational waves from coalescing black holes was announced.^[70] Besides LIGO, many other gravitational-wave observatories (detectors) are under construction.^[71]

Other areas of inquiry

Cosmologists also study:

• Whether primordial black holes were formed in our universe, and what happened to them.^[72]
• Detection of cosmic rays with energies above the GZK cutoff,^[73] and whether it signals a failure of special relativity at high energies.
• The equivalence principle,^[36] whether or not Einstein's general theory of relativity is the correct theory of gravitation,^[74] and if the fundamental laws of physics are the same everywhere in the universe.^[75]
• The increasing complexity of universal structures, an example being the progressively greater energy rate density.^[76]

Meet the Nanomachines That Could Drive a Medical Revolution

By Tapas Sen Apr 21, 2016

Original link:  https://singularityhub.com/2016/04/21/meet-the-nanomachines-that-could-drive-a-medical-revolution/

A group of physicists recently built the smallest engine ever created from just a single atom. Like any other engine it converts heat energy into movement — but it does so on a smaller scale than ever seen before. The atom is trapped in a cone of electromagnetic energy and lasers are used to heat it up and cool it down, which causes the atom to move back and forth in the cone like an engine piston.
The scientists from the University of Mainz in Germany who are behind the invention don’t have a particular use in mind for the engine. But it’s a good illustration of how we are increasingly able to replicate the everyday machines we rely on at a tiny scale. This is opening the way for some exciting possibilities in the future, particularly in the use of nanorobots in medicine, that could be sent into the body to release targeted drugs or even fight diseases such as cancer.

Nanotechnology deals with ultra-small objects equivalent to one billionth of a meter in size, which sounds an impossibly tiny scale at which to build machines. But size is relative to how close you are to an object. We can’t see things at the nanoscale with the naked eye, just as we can’t see the outer planets of the solar system. Yet if we zoom in — with a telescope for the planets or a powerful electron microscope for nano-objects — then we change the frame of reference and things look very different.

However, even after getting a closer look, we still can’t build machines at the nanoscale using conventional engineering tools. While regular machines, such as the internal combustion engines in most cars, operate according to the rules of physics laid out by Isaac Newton, things at the nanoscale follow the more complex laws of quantum mechanics. So we need different tools that take into account the quantum world in order to manipulate atoms and molecules in a way that uses them as building blocks for nanomachines. Here are four more tiny machines that could have a big impact.

Graphene engine for nanorobots

Researchers from Singapore have recently demonstrated a simple but nano-sized engine made from a highly elastic piece of graphene. Graphene is a two-dimensional sheet of carbon atoms that has exceptional mechanical strength. Inserting some chlorine and fluorine molecules into the graphene lattice and firing a laser at it causes the sheet to expand. Rapidly turning the laser on and off makes the graphene pump back and forth like the piston in an internal combustion engine.

The researchers think the graphene nano-engine could be used to power tiny robots, for example to attack cancer cells in the body. Or it could be used in a so-called “lab-on-a-chip” — a device that shrinks the functions of a chemistry lab into tiny package that can be used for rapid blood tests, among other things.

Frictionless nano-rotor

Molecular motor. Image credit: Palma, C.-A.; Kühne, D.; Klappenberger, F.; Barth, J.V.; Technische Universität München

The rotors that produce movement in machines such as aircraft engines and fans all usually suffer from friction, which limits their performance. Nanotechnology can be used to create a motor from a single molecule, which can rotate without any friction. Normal rotors interact with the air according to Newton’s laws as they spin round and so experience friction. But, at the nanoscale, molecular rotors follow quantum law, meaning they don’t interact with the air in the same way and so friction doesn’t affect their performance.

Nature has actually already shown us that molecular motors are possible. Certain proteins can travel along a surface using a rotating mechanism that create movement from chemical energy. These motor proteins are what cause cells to contract and so are responsible for our muscle movements.

Researchers from Germany recently reported creating a molecular rotor by placing moving molecules inside a tiny hexagonal hole known as a nanopore in a thin piece of silver. The position and movement of the molecules meant they began to rotate around the hole like a rotor. Again, this form of nano-engine could be used to power a tiny robot around the body.

Controllable nano-rockets

A rocket is the fastest man-made vehicle that can freely travel across the universe. Several groups of researchers have recently constructed a high-speed, remote-controlled nanoscale version of a rocket by combining nanoparticles with biological molecules.

In one case, the body of the rocket was made from a polystyrene bead covered in gold and chromium. This was attached to multiple “catalytic engine” molecules using strands of DNA. When placed in a solution of hydrogen peroxide, the engine molecules caused a chemical reaction that produced oxygen bubbles, forcing the rocket to move in the opposite direction. Shining a beam of ultra-violet light on one side of the rocket causes the DNA to break apart, detaching the engines and changing the rocket’s direction of travel. The researchers hope to develop the rocket so it can be used in any environment, for example to deliver drugs to a target area of the body.

Magnetic nano-vehicles for carrying drugs

Magnetic nanoparticles. Image credit: Tapas Sen, author provided

My own research group is among those working on a simpler way to carry drugs through the body that is already being explored with magnetic nanoparticles. Drugs are injected into a magnetic shell structure that can expand in the presence of heat or light. This means that, once inserted into the body, they can be guided to the target area using magnets and then activated to expand and release their drug.

The technology is also being studied for medical imaging. Creating the nanoparticles to gather in certain tissues and then scanning the body with a magnetic resonance imaging (MRI) could help highlight problems such as diabetes.

Nanotech could make humans immortal by 2040, futurist says

By Sharon Gaudin

Senior Writer, Computerworld | Oct 1, 2009
Updated to  Jun 30, 2018

Original link:  https://www.computerworld.com/article/2528330/app-development/nanotech-could-make-humans-immortal-by-2040--futurist-says.html 
 

In 20 or 30 years, we'll have microscopic machines traveling through our bodies, repairing damaged cells and organs, effectively wiping out diseases. The nanotechnology will also be used to back up our memories and personalities.

In an interview with Computerworld, author and futurist Ray Kurzweil said that anyone alive come 2040 or 2050 could be close to immortal. The quickening advance of nanotechnology means that the human condition will shift into more of a collaboration of man and machine, as nanobots flow through human blood streams and eventually even replace biological blood, he added.

That may sound like something out of a sci-fi movie, but Kurzweil, a member of the Inventor's Hall of Fame and a recipient of the National Medal of Technology, says that research well underway today is leading to a time when a combination of nanotechnology and biotechnology will wipe out cancer, Alzheimer's disease, obesity and diabetes.

It'll also be a time when humans will augment their natural cognitive powers and add years to their lives, Kurzweil said.

"It's radical life extension," Kurzweil said. "The full realization of nanobots will basically eliminate biological disease and aging. I think we'll see widespread use in 20 years of [nanotech] devices that perform certain functions for us. In 30 or 40 years, we will overcome disease and aging. The nanobots will scout out organs and cells that need repairs and simply fix them. It will lead to profound extensions of our health and longevity."

Of course, people will still be struck by lightning or hit by a bus, but much more trauma will be repairable. If nanobots swim in, or even replace, biological blood, then wounds could be healed almost instantly. Limbs could be regrown. Backed up memories and personalities could be accessed after a head trauma.

Today, researchers at MIT already are using nanoparticles to deliver killer genes that battle late-stage cancer. The university reported just last month the nano-based treatment killed ovarian cancer, which is considered to be one of the most deadly cancers, in mice.

And earlier this year, scientists at the University of London reported using nanotechnology to blast cancer cells in mice with "tumor busting" genes, giving new hope to patients with inoperable tumors. So far, tests have shown that the new technique leaves healthy cells undamaged.

With this kind of work going on now, Kurzweil says that by 2024 we'll be adding a year to our life expectancy with every year that passes. "The sense of time will be running in and not running out," he added. "Within 15 years, we will reverse this loss of remaining life expectancy. We will be adding more time than is going by."

And in 35 to 40 years, we basically will be immortal, according to the man who wrote The Age of Spiritual Machines and The Singularity is Near: When Humans Transcend Biology.

Kurzweil also maintains that adding microscopic machines to our bodies won't make us any less human than we are today or were 500 years ago.

"The definition of human is that we are the species that goes beyond our limitations and changes who we are," he said. "If that wasn't the case, you and I wouldn't be around because at one point life expectancy was 23. We've extended ourselves in many ways. This is an extension of who we are. Ever since we picked up a stick to reach a higher branch, we've extended who we are through tools. It's the nature of human beings to change who we are."

But that doesn't mean there aren't parts of this future that don't worry him. With nanotechnology so advanced that it can travel through our bodies and affect great change on them, come dangers as well as benefits.

The nanobots, he explained, will be self-replicating and engineers will have to harness and contain that replication.

"You could have some self-replicating nanobot that could create copies of itself... and ultimately, within 90 replications, it could devour the body it's in or all humans if it becomes a non-biological plague," said Kurzweil. "Technology is not a utopia. It's a double-edged sword and always has been since we first had fire."

System dynamics

From Wikipedia, the free encyclopedia

 

Dynamic stock and flow diagram of model New product adoption (model from article by John Sterman 2001)

System dynamics (SD) is an approach to understanding the nonlinear behaviour of complex systems over time using stocks, flows, internal feedback loops, table functions and time delays.

Overview

System dynamics is a methodology and mathematical modeling technique to frame, understand, and discuss complex issues and problems. Originally developed in the 1950s to help corporate managers improve their understanding of industrial processes, SD is currently being used throughout the public and private sector for policy analysis and design.^[2]

Convenient graphical user interface (GUI) system dynamics software developed into user friendly versions by the 1990s and have been applied to diverse systems. SD models solve the problem of simultaneity (mutual causation) by updating all variables in small time increments with positive and negative feedbacks and time delays structuring the interactions and control. The best known SD model is probably the 1972 The Limits to Growth. This model forecast that exponential growth of population and capital, with finite resource sources and sinks and perception delays, would lead to economic collapse during the 21st century under a wide variety of growth scenarios.

System dynamics is an aspect of systems theory as a method to understand the dynamic behavior of complex systems. The basis of the method is the recognition that the structure of any system, the many circular, interlocking, sometimes time-delayed relationships among its components, is often just as important in determining its behavior as the individual components themselves. Examples are chaos theory and social dynamics. It is also claimed that because there are often properties-of-the-whole which cannot be found among the properties-of-the-elements, in some cases the behavior of the whole cannot be explained in terms of the behavior of the parts.

History

System dynamics was created during the mid-1950s^[3] by Professor Jay Forrester of the Massachusetts Institute of Technology. In 1956, Forrester accepted a professorship in the newly formed MIT Sloan School of Management. His initial goal was to determine how his background in science and engineering could be brought to bear, in some useful way, on the core issues that determine the success or failure of corporations. Forrester's insights into the common foundations that underlie engineering, which led to the creation of system dynamics, were triggered, to a large degree, by his involvement with managers at General Electric (GE) during the mid-1950s. At that time, the managers at GE were perplexed because employment at their appliance plants in Kentucky exhibited a significant three-year cycle. The business cycle was judged to be an insufficient explanation for the employment instability. From hand simulations (or calculations) of the stock-flow-feedback structure of the GE plants, which included the existing corporate decision-making structure for hiring and layoffs, Forrester was able to show how the instability in GE employment was due to the internal structure of the firm and not to an external force such as the business cycle. These hand simulations were the start of the field of system dynamics.^[2]

During the late 1950s and early 1960s, Forrester and a team of graduate students moved the emerging field of system dynamics from the hand-simulation stage to the formal computer modeling stage. Richard Bennett created the first system dynamics computer modeling language called SIMPLE (Simulation of Industrial Management Problems with Lots of Equations) in the spring of 1958. In 1959, Phyllis Fox and Alexander Pugh wrote the first version of DYNAMO (DYNAmic MOdels), an improved version of SIMPLE, and the system dynamics language became the industry standard for over thirty years. Forrester published the first, and still classic, book in the field titled Industrial Dynamics in 1961.^[2]

From the late 1950s to the late 1960s, system dynamics was applied almost exclusively to corporate/managerial problems. In 1968, however, an unexpected occurrence caused the field to broaden beyond corporate modeling. John F. Collins, the former mayor of Boston, was appointed a visiting professor of Urban Affairs at MIT. The result of the Collins-Forrester collaboration was a book titled Urban Dynamics. The Urban Dynamics model presented in the book was the first major non-corporate application of system dynamics.^[2]

The second major noncorporate application of system dynamics came shortly after the first. In 1970, Jay Forrester was invited by the Club of Rome to a meeting in Bern, Switzerland. The Club of Rome is an organization devoted to solving what its members describe as the "predicament of mankind"—that is, the global crisis that may appear sometime in the future, due to the demands being placed on the Earth's carrying capacity (its sources of renewable and nonrenewable resources and its sinks for the disposal of pollutants) by the world's exponentially growing population. At the Bern meeting, Forrester was asked if system dynamics could be used to address the predicament of mankind. His answer, of course, was that it could. On the plane back from the Bern meeting, Forrester created the first draft of a system dynamics model of the world's socioeconomic system. He called this model WORLD1. Upon his return to the United States, Forrester refined WORLD1 in preparation for a visit to MIT by members of the Club of Rome. Forrester called the refined version of the model WORLD2. Forrester published WORLD2 in a book titled World Dynamics.^[2]

Topics in systems dynamics

The elements of system dynamics diagrams are feedback, accumulation of flows into stocks and time delays.

As an illustration of the use of system dynamics, imagine an organisation that plans to introduce an innovative new durable consumer product. The organisation needs to understand the possible market dynamics in order to design marketing and production plans.

Causal loop diagrams

In the system dynamics methodology, a problem or a system (e.g., ecosystem, political system or mechanical system) may be represented as a causal loop diagram.^[4] A causal loop diagram is a simple map of a system with all its constituent components and their interactions. By capturing interactions and consequently the feedback loops (see figure below), a causal loop diagram reveals the structure of a system. By understanding the structure of a system, it becomes possible to ascertain a system’s behavior over a certain time period.^[5]
The causal loop diagram of the new product introduction may look as follows:

Causal loop diagram of New product adoption model

There are two feedback loops in this diagram. The positive reinforcement (labeled R) loop on the right indicates that the more people have already adopted the new product, the stronger the word-of-mouth impact. There will be more references to the product, more demonstrations, and more reviews. This positive feedback should generate sales that continue to grow.

The second feedback loop on the left is negative reinforcement (or "balancing" and hence labeled B). Clearly, growth cannot continue forever, because as more and more people adopt, there remain fewer and fewer potential adopters.

Both feedback loops act simultaneously, but at different times they may have different strengths. Thus one might expect growing sales in the initial years, and then declining sales in the later years. However, in general a causal loop diagram does not specify the structure of a system sufficiently to permit determination of its behavior from the visual representation alone.^[6]

Stock and flow diagrams

Causal loop diagrams aid in visualizing a system’s structure and behavior, and analyzing the system qualitatively. To perform a more detailed quantitative analysis, a causal loop diagram is transformed to a stock and flow diagram. A stock and flow model helps in studying and analyzing the system in a quantitative way; such models are usually built and simulated using computer software.
A stock is the term for any entity that accumulates or depletes over time. A flow is the rate of change in a stock.

A flow is the rate of accumulation of the stock

In our example, there are two stocks: Potential adopters and Adopters. There is one flow: New adopters. For every new adopter, the stock of potential adopters declines by one, and the stock of adopters increases by one.

Stock and flow diagram of New product adoption model

Equations

The real power of system dynamics is utilised through simulation. Although it is possible to perform the modeling in a spreadsheet, there are a variety of software packages that have been optimised for this.

The steps involved in a simulation are:

• Define the problem boundary
• Identify the most important stocks and flows that change these stock levels
• Identify sources of information that impact the flows
• Identify the main feedback loops
• Draw a causal loop diagram that links the stocks, flows and sources of information
• Write the equations that determine the flows
• Estimate the parameters and initial conditions. These can be estimated using statistical methods, expert opinion, market research data or other relevant sources of information.^[7]
• Simulate the model and analyse results.

In this example, the equations that change the two stocks via the flow are:

${\displaystyle \ {\mbox{Potential adopters}}=\int _{0}^{t}{\mbox{-New adopters }}\,dt}$
${\displaystyle \ {\mbox{Adopters}}=\int _{0}^{t}{\mbox{New adopters }}\,dt}$

Equations in discrete time

List of all the equations in discrete time, in their order of execution in each year, for years 1 to 15 :

${\displaystyle 1)\ {\mbox{Probability that contact has not yet adopted}}={\mbox{Potential adopters}}/({\mbox{Potential adopters }}+{\mbox{ Adopters}})}$
${\displaystyle 2)\ {\mbox{Imitators}}=q\cdot {\mbox{Adopters}}\cdot {\mbox{Probability that contact has not yet adopted}}}$
${\displaystyle 3)\ {\mbox{Innovators}}=p\cdot {\mbox{Potential adopters}}}$
${\displaystyle 4)\ {\mbox{New adopters}}={\mbox{Innovators}}+{\mbox{Imitators}}}$
${\displaystyle 4.1)\ {\mbox{Potential adopters}}\ -={\mbox{New adopters }}}$
${\displaystyle 4.2)\ {\mbox{Adopters}}\ +={\mbox{New adopters }}}$

${\displaystyle \ p=0.03}$
${\displaystyle \ q=0.4}$

Dynamic simulation results

The dynamic simulation results show that the behaviour of the system would be to have growth in adopters that follows a classic s-curve shape.

The increase in adopters is very slow initially, then exponential growth for a period, followed ultimately by saturation.

Dynamic stock and flow diagram of New product adoption

model

 

Stocks and flows values for years = 0 to 15

Equations in continuous time

To get intermediate values and better accuracy, the model can run in continuous time: we multiply the number of units of time and we proportionally divide values that change stock levels. In this example we multiply the 15 years by 4 to obtain 60 trimesters, and we divide the value of the flow by 4.
Dividing the value is the simplest with the Euler method, but other methods could be employed instead, such as Runge–Kutta methods.

List of the equations in continuous time for trimesters = 1 to 60 :

• They are the same equations as in the section Equation in discrete time above, except equations 4.1 and 4.2 replaced by following :

${\displaystyle 10)\ {\mbox{Valve New adopters}}\ ={\mbox{New adopters}}\cdot TimeStep}$
${\displaystyle 10.1)\ {\mbox{Potential adopters}}\ -={\mbox{Valve New adopters}}}$
${\displaystyle 10.2)\ {\mbox{Adopters}}\ +={\mbox{Valve New adopters }}}$

${\displaystyle \ TimeStep=1/4}$

• In the below stock and flow diagram, the intermediate flow 'Valve New adopters' calculates the equation :

${\displaystyle \ {\mbox{Valve New adopters}}\ ={\mbox{New adopters }}\cdot TimeStep}$

Dynamic stock and flow diagram of New product adoption 

model in continuous time

Application

System dynamics has found application in a wide range of areas, for example population, ecological and economic systems, which usually interact strongly with each other.

System dynamics have various "back of the envelope" management applications. They are a potent tool to:

• Teach system thinking reflexes to persons being coached
• Analyze and compare assumptions and mental models about the way things work
• Gain qualitative insight into the workings of a system or the consequences of a decision
• Recognize archetypes of dysfunctional systems in everyday practice

Computer software is used to simulate a system dynamics model of the situation being studied. Running "what if" simulations to test certain policies on such a model can greatly aid in understanding how the system changes over time. System dynamics is very similar to systems thinking and constructs the same causal loop diagrams of systems with feedback. However, system dynamics typically goes further and utilises simulation to study the behaviour of systems and the impact of alternative policies.^[8]

System dynamics has been used to investigate resource dependencies, and resulting problems, in product development.^[9][10]

A system dynamics approach to macroeconomics, known as Minsky, has been developed by the economist Steve Keen.^[11] This has been used to successfully model world economic behaviour from the apparent stability of the Great Moderation to the sudden unexpected Financial crisis of 2007–08.

Example

Causal loop diagram of a model examining the growth or

decline of a life insurance company.^[12]

The figure above is a causal loop diagram of a system dynamics model created to examine forces that may be responsible for the growth or decline of life insurance companies in the United Kingdom. A number of this figure's features are worth mentioning. The first is that the model's negative feedback loops are identified by C's, which stand for Counteracting loops. The second is that double slashes are used to indicate places where there is a significant delay between causes (i.e., variables at the tails of arrows) and effects (i.e., variables at the heads of arrows). This is a common causal loop diagramming convention in system dynamics. Third, is that thicker lines are used to identify the feedback loops and links that author wishes the audience to focus on. This is also a common system dynamics diagramming convention. Last, it is clear that a decision maker would find it impossible to think through the dynamic behavior inherent in the model, from inspection of the figure alone.