Molecular vibration

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Molecular_vibration 

A molecular vibration is a periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The typical vibrational frequencies, range from less than 10¹³ Hz to approximately 10¹⁴ Hz, corresponding to wavenumbers of approximately 300 to 3000 cm⁻¹.

In general, a non-linear molecule with N atoms has 3N – 6 normal modes of vibration, but a linear molecule has 3N – 5 modes, because rotation about the molecular axis cannot be observed. A diatomic molecule has one normal mode of vibration, since it can only stretch or compress the single bond. Vibrations of polyatomic molecules are described in terms of normal modes, which are independent of each other, but each normal mode involves simultaneous vibrations of different parts of the molecule.

A molecular vibration is excited when the molecule absorbs energy, ΔE, corresponding to the vibration's frequency, ν, according to the relation ΔE = hν, where h is Planck's constant. A fundamental vibration is evoked when one such quantum of energy is absorbed by the molecule in its ground state. When multiple quanta are absorbed, the first and possibly higher overtones are excited.

To a first approximation, the motion in a normal vibration can be described as a kind of simple harmonic motion. In this approximation, the vibrational energy is a quadratic function (parabola) with respect to the atomic displacements and the first overtone has twice the frequency of the fundamental. In reality, vibrations are anharmonic and the first overtone has a frequency that is slightly lower than twice that of the fundamental. Excitation of the higher overtones involves progressively less and less additional energy and eventually leads to dissociation of the molecule, because the potential energy of the molecule is more like a Morse potential or more accurately, a Morse/Long-range potential.

The vibrational states of a molecule can be probed in a variety of ways. The most direct way is through infrared spectroscopy, as vibrational transitions typically require an amount of energy that corresponds to the infrared region of the spectrum. Raman spectroscopy, which typically uses visible light, can also be used to measure vibration frequencies directly. The two techniques are complementary and comparison between the two can provide useful structural information such as in the case of the rule of mutual exclusion for centrosymmetric molecules.

Vibrational excitation can occur in conjunction with electronic excitation in the ultraviolet-visible region. The combined excitation is known as a vibronic transition, giving vibrational fine structure to electronic transitions, particularly for molecules in the gas state.

Simultaneous excitation of a vibration and rotations gives rise to vibration-rotation spectra.

Number of vibrational modes

For a molecule with N atoms, the positions of all N nuclei depend on a total of 3N coordinates, so that the molecule has 3N degrees of freedom including translation, rotation and vibration. Translation corresponds to movement of the center of mass whose position can be described by 3 cartesian coordinates.

A nonlinear molecule can rotate about any of three mutually perpendicular axes and therefore has 3 rotational degrees of freedom. For a linear molecule, rotation about the molecular axis does not involve movement of any atomic nucleus, so there are only 2 rotational degrees of freedom which can vary the atomic coordinates.

An equivalent argument is that the rotation of a linear molecule changes the direction of the molecular axis in space, which can be described by 2 coordinates corresponding to latitude and longitude. For a nonlinear molecule, the direction of one axis is described by these two coordinates, and the orientation of the molecule about this axis provides a third rotational coordinate.

The number of vibrational modes is therefore 3N minus the number of translational and rotational degrees of freedom, or 3N–5 for linear and 3N–6 for nonlinear molecules.

Vibrational coordinates

The coordinate of a normal vibration is a combination of changes in the positions of atoms in the molecule. When the vibration is excited the coordinate changes sinusoidally with a frequency ν, the frequency of the vibration.

Internal coordinates

Internal coordinates are of the following types, illustrated with reference to the planar molecule ethylene,

• Stretching: a change in the length of a bond, such as C–H or C–C
• Bending: a change in the angle between two bonds, such as the HCH angle in a methylene group
• Rocking: a change in angle between a group of atoms, such as a methylene group and the rest of the molecule.
• Wagging: a change in angle between the plane of a group of atoms, such as a methylene group and a plane through the rest of the molecule,
• Twisting: a change in the angle between the planes of two groups of atoms, such as a change in the angle between the two methylene groups.
• Out–of–plane: a change in the angle between any one of the C–H bonds and the plane defined by the remaining atoms of the ethylene molecule. Another example is in BF₃ when the boron atom moves in and out of the plane of the three fluorine atoms.

In a rocking, wagging or twisting coordinate the bond lengths within the groups involved do not change. The angles do. Rocking is distinguished from wagging by the fact that the atoms in the group stay in the same plane.

In ethene there are 12 internal coordinates: 4 C–H stretching, 1 C–C stretching, 2 H–C–H bending, 2 CH₂ rocking, 2 CH₂ wagging, 1 twisting. Note that the H–C–C angles cannot be used as internal coordinates as the angles at each carbon atom cannot all increase at the same time.

Vibrations of a methylene group (–CH₂–) in a molecule for illustration

The atoms in a CH₂ group, commonly found in organic compounds, can vibrate in six different ways: symmetric and asymmetric stretching, scissoring, rocking, wagging and twisting as shown here:

Symmetrical stretching	Asymmetrical stretching	Scissoring (Bending)
Rocking	Wagging	Twisting

(These figures do not represent the "recoil" of the C atoms, which, though necessarily present to balance the overall movements of the molecule, are much smaller than the movements of the lighter H atoms).

Symmetry–adapted coordinates

Symmetry–adapted coordinates may be created by applying a projection operator to a set of internal coordinates. The projection operator is constructed with the aid of the character table of the molecular point group. For example, the four (un–normalized) C–H stretching coordinates of the molecule ethene are given by

${\displaystyle Q_{s1}=q_{1}+q_{2}+q_{3}+q_{4}\!}$

${\displaystyle Q_{s2}=q_{1}+q_{2}-q_{3}-q_{4}\!}$

${\displaystyle Q_{s3}=q_{1}-q_{2}+q_{3}-q_{4}\!}$

${\displaystyle Q_{s4}=q_{1}-q_{2}-q_{3}+q_{4}\!}$

where ${\displaystyle q_{1}-q_{4}}$ are the internal coordinates for stretching of each of the four C–H bonds.

Illustrations of symmetry–adapted coordinates for most small molecules can be found in Nakamoto.^[6]

Normal coordinates

The normal coordinates, denoted as Q, refer to the positions of atoms away from their equilibrium positions, with respect to a normal mode of vibration. Each normal mode is assigned a single normal coordinate, and so the normal coordinate refers to the "progress" along that normal mode at any given time. Formally, normal modes are determined by solving a secular determinant, and then the normal coordinates (over the normal modes) can be expressed as a summation over the cartesian coordinates (over the atom positions). The normal modes diagonalize the matrix governing the molecular vibrations, so that each normal mode is an independent molecular vibration. If the molecule possesses symmetries, the normal modes "transform as" an irreducible representation under its point group. The normal modes are determined by applying group theory, and projecting the irreducible representation onto the cartesian coordinates. For example, when this treatment is applied to CO₂, it is found that the C=O stretches are not independent, but rather there is an O=C=O symmetric stretch and an O=C=O asymmetric stretch:

• symmetric stretching: the sum of the two C–O stretching coordinates; the two C–O bond lengths change by the same amount and the carbon atom is stationary. Q = q₁ + q₂
• asymmetric stretching: the difference of the two C–O stretching coordinates; one C–O bond length increases while the other decreases. Q = q₁ - q₂

When two or more normal coordinates belong to the same irreducible representation of the molecular point group (colloquially, have the same symmetry) there is "mixing" and the coefficients of the combination cannot be determined a priori. For example, in the linear molecule hydrogen cyanide, HCN, The two stretching vibrations are

• principally C–H stretching with a little C–N stretching; Q₁ = q₁ + a q₂ (a << 1)
• principally C–N stretching with a little C–H stretching; Q₂ = b q₁ + q₂ (b << 1)

The coefficients a and b are found by performing a full normal coordinate analysis by means of the Wilson GF method.

Newtonian mechanics

The HCl molecule as an anharmonic oscillator vibrating at energy level E₃. D₀ is dissociation energy here, r₀ bond length, U potential energy. Energy is expressed in wavenumbers. The hydrogen chloride molecule is attached to the coordinate system to show bond length changes on the curve.

Perhaps surprisingly, molecular vibrations can be treated using Newtonian mechanics to calculate the correct vibration frequencies. The basic assumption is that each vibration can be treated as though it corresponds to a spring. In the harmonic approximation the spring obeys Hooke's law: the force required to extend the spring is proportional to the extension. The proportionality constant is known as a force constant, k. The anharmonic oscillator is considered elsewhere.

${\displaystyle \mathrm {Force} =-kQ\!}$

By Newton's second law of motion this force is also equal to a reduced mass, μ, times acceleration.

${\displaystyle \mathrm {Force} =\mu {\frac {d^{2}Q}{dt^{2}}}}$

Since this is one and the same force the ordinary differential equation follows.

${\displaystyle \mu {\frac {d^{2}Q}{dt^{2}}}+kQ=0}$

The solution to this equation of simple harmonic motion is

${\displaystyle Q(t)=A\cos(2\pi \nu t);\ \ \nu ={1 \over {2\pi }}{\sqrt {k \over \mu }}.\!}$

A is the maximum amplitude of the vibration coordinate Q. It remains to define the reduced mass, μ. In general, the reduced mass of a diatomic molecule, AB, is expressed in terms of the atomic masses, m_A and m_B, as

${\displaystyle {\frac {1}{\mu }}={\frac {1}{m_{A}}}+{\frac {1}{m_{B}}}.}$

The use of the reduced mass ensures that the centre of mass of the molecule is not affected by the vibration. In the harmonic approximation the potential energy of the molecule is a quadratic function of the normal coordinate. It follows that the force-constant is equal to the second derivative of the potential energy.

${\displaystyle k={\frac {\partial ^{2}V}{\partial Q^{2}}}}$

When two or more normal vibrations have the same symmetry a full normal coordinate analysis must be performed (see GF method). The vibration frequencies,ν_i are obtained from the eigenvalues,λ_i, of the matrix product GF. G is a matrix of numbers derived from the masses of the atoms and the geometry of the molecule. F is a matrix derived from force-constant values. Details concerning the determination of the eigenvalues can be found in.

Quantum mechanics

In the harmonic approximation the potential energy is a quadratic function of the normal coordinates. Solving the Schrödinger wave equation, the energy states for each normal coordinate are given by

${\displaystyle E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!}$,

where n is a quantum number that can take values of 0, 1, 2 ... In molecular spectroscopy where several types of molecular energy are studied and several quantum numbers are used, this vibrational quantum number is often designated as v.

The difference in energy when n (or v) changes by 1 is therefore equal to ${\displaystyle h\nu }$, the product of the Planck constant and the vibration frequency derived using classical mechanics. For a transition from level n to level n+1 due to absorption of a photon, the frequency of the photon is equal to the classical vibration frequency ${\displaystyle \nu }$ (in the harmonic oscillator approximation).

See quantum harmonic oscillator for graphs of the first 5 wave functions, which allow certain selection rules to be formulated. For example, for a harmonic oscillator transitions are allowed only when the quantum number n changes by one,

${\displaystyle \Delta n=\pm 1}$

but this does not apply to an anharmonic oscillator; the observation of overtones is only possible because vibrations are anharmonic. Another consequence of anharmonicity is that transitions such as between states n=2 and n=1 have slightly less energy than transitions between the ground state and first excited state. Such a transition gives rise to a hot band. To describe vibrational levels of an anharmonic oscillator, Dunham expansion is used.

Intensities

In an infrared spectrum the intensity of an absorption band is proportional to the derivative of the molecular dipole moment with respect to the normal coordinate. Likewise, the intensity of Raman bands depends on the derivative of polarizability with respect to the normal coordinate. There is also a dependence on the fourth-power of the wavelength of the laser used.

Quantum network

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Quantum_network 

 

This article is about the implementation and operation of quantum networks. For a mathematical description of quantum communication channels, see Quantum channel.

Quantum networks form an important element of quantum computing and quantum communication systems. Quantum networks facilitate the transmission of information in the form of quantum bits, also called qubits, between physically separated quantum processors. A quantum processor is a small quantum computer being able to perform quantum logic gates on a certain number of qubits. Quantum networks work in a similar way to classical networks. The main difference is that quantum networking, like quantum computing, is better at solving certain problems, such as modeling quantum systems.

Basics

Quantum networks for computation

Networked quantum computing or distributed quantum computing works by linking multiple quantum processors through a quantum network by sending qubits in-between them. Doing this creates a quantum computing cluster and therefore creates more computing potential. Less powerful computers can be linked in this way to create one more powerful processor. This is analogous to connecting several classical computers to form a computer cluster in classical computing. Like classical computing this system is scale-able by adding more and more quantum computers to the network. Currently quantum processors are only separated by short distances.

Quantum networks for communication

In the realm of quantum communication, one wants to send qubits from one quantum processor to another over long distances. This way local quantum networks can be intra connected into a quantum internet. A quantum internet supports many applications, which derive their power from the fact that by creating quantum entangled qubits, information can be transmitted between the remote quantum processors. Most applications of a quantum internet require only very modest quantum processors. For most quantum internet protocols, such as quantum key distribution in quantum cryptography, it is sufficient if these processors are capable of preparing and measuring only a single qubit at a time. This is in contrast to quantum computing where interesting applications can only be realized if the (combined) quantum processors can easily simulate more qubits than a classical computer (around 60). Quantum internet applications require only small quantum processors, often just a single qubit, because quantum entanglement can already be realized between just two qubits. A simulation of an entangled quantum system on a classical computer cannot simultaneously provide the same security and speed.

Overview of the elements of a quantum network

The basic structure of a quantum network and more generally a quantum internet is analogous to a classical network. First, we have end nodes on which applications are ultimately run. These end nodes are quantum processors of at least one qubit. Some applications of a quantum internet require quantum processors of several qubits as well as a quantum memory at the end nodes.

Second, to transport qubits from one node to another, we need communication lines. For the purpose of quantum communication, standard telecom fibers can be used. For networked quantum computing, in which quantum processors are linked at short distances, different wavelengths are chosen depending on the exact hardware platform of the quantum processor.

Third, to make maximum use of communication infrastructure, one requires optical switches capable of delivering qubits to the intended quantum processor. These switches need to preserve quantum coherence, which makes them more challenging to realize than standard optical switches.

Finally, one requires a quantum repeater to transport qubits over long distances. Repeaters appear in-between end nodes. Since qubits cannot be copied, classical signal amplification is not possible. By necessity, a quantum repeater works in a fundamentally different way than a classical repeater.

Elements of a quantum network

End nodes: quantum processors

End nodes can both receive and emit information. Telecommunication lasers and parametric down-conversion combined with photodetectors can be used for quantum key distribution. In this case, the end nodes can in many cases be very simple devices consisting only of beamsplitters and photodetectors.

However, for many protocols more sophisticated end nodes are desirable. These systems provide advanced processing capabilities and can also be used as quantum repeaters. Their chief advantage is that they can store and retransmit quantum information without disrupting the underlying quantum state. The quantum state being stored can either be the relative spin of an electron in a magnetic field or the energy state of an electron. They can also perform quantum logic gates.

One way of realizing such end nodes is by using color centers in diamond, such as the nitrogen-vacancy center. This system forms a small quantum processor featuring several qubits. NV centers can be utilized at room temperatures. Small scale quantum algorithms and quantum error correction has already been demonstrated in this system, as well as the ability to entangle two remote quantum processors, and perform deterministic quantum teleportation.

Another possible platform are quantum processors based on Ion traps, which utilize radio-frequency magnetic fields and lasers. In a multispecies trapped-ion node network, photons entangled with a parent atom are used to entangle different nodes. Also, cavity quantum electrodynamics (Cavity QED) is one possible method of doing this. In Cavity QED, photonic quantum states can be transferred to and from atomic quantum states stored in single atoms contained in optical cavities. This allows for the transfer of quantum states between single atoms using optical fiber in addition to the creation of remote entanglement between distant atoms.

Communication lines: physical layer

Over long distances, the primary method of operating quantum networks is to use optical networks and photon-based qubits. This is due to optical networks having a reduced chance of decoherence. Optical networks have the advantage of being able to re-use existing optical fiber. Alternately, free space networks can be implemented that transmit quantum information through the atmosphere or through a vacuum.

Fiber optic networks

Optical networks using existing telecommunication fiber can be implemented using hardware similar to existing telecommunication equipment. This fiber can be either single-mode or multi-mode, with multi-mode allowing for more precise communication. At the sender, a single photon source can be created by heavily attenuating a standard telecommunication laser such that the mean number of photons per pulse is less than 1. For receiving, an avalanche photodetector can be used. Various methods of phase or polarization control can be used such as interferometers and beam splitters. In the case of entanglement based protocols, entangled photons can be generated through spontaneous parametric down-conversion. In both cases, the telecom fiber can be multiplexed to send non-quantum timing and control signals.

Free space networks

Free space quantum networks operate similar to fiber optic networks but rely on line of sight between the communicating parties instead of using a fiber optic connection. Free space networks can typically support higher transmission rates than fiber optic networks and do not have to account for polarization scrambling caused by optical fiber. However, over long distances, free space communication is subject to an increased chance of environmental disturbance on the photons.

Importantly, free space communication is also possible from a satellite to the ground. A quantum satellite capable of entanglement distribution over a distance of 1,203 km has been demonstrated. The experimental exchange of single photons from a global navigation satellite system at a slant distance of 20,000 km has also been reported. These satellites can play an important role in linking smaller ground-based networks over larger distances.

Repeaters

Long distance communication is hindered by the effects of signal loss and decoherence inherent to most transport mediums such as optical fiber. In classical communication, amplifiers can be used to boost the signal during transmission, but in a quantum network amplifiers cannot be used since qubits cannot be copied – known as the no-cloning theorem. That is, to implement an amplifier, the complete state of the flying qubit would need to be determined, something which is both unwanted and impossible.

Trusted repeaters

An intermediary step which allows the testing of communication infrastructure are trusted repeaters. Importantly, a trusted repeater cannot be used to transmit qubits over long distances. Instead, a trusted repeater can only be used to perform quantum key distribution with the additional assumption that the repeater is trusted. Consider two end nodes A and B, and a trusted repeater R in the middle. A and R now perform quantum key distribution to generate a key ${\displaystyle k_{AR}}$. Similarly, R and B run quantum key distribution to generate a key ${\displaystyle k_{RB}}$. A and B can now obtain a key ${\displaystyle k_{AB}}$ between themselves as follows: A sends ${\displaystyle k_{AB}}$ to R encrypted with the key ${\displaystyle k_{AR}}$. R decrypts to obtain ${\displaystyle k_{AB}}$. R then re-encrypts ${\displaystyle k_{AB}}$ using the key ${\displaystyle k_{RB}}$ and sends it to B. B decrypts to obtain ${\displaystyle k_{AB}}$. A and B now share the key ${\displaystyle k_{AB}}$. The key is secure from an outside eavesdropper, but clearly the repeater R also knows ${\displaystyle k_{AB}}$. This means that any subsequent communication between A and B does not provide end to end security, but is only secure as long as A and B trust the repeater R.

Quantum repeaters

Diagram for quantum teleportation of a photon

A true quantum repeater allows the end to end generation of quantum entanglement, and thus - by using quantum teleportation - the end to end transmission of qubits. In quantum key distribution protocols one can test for such entanglement. This means that when making encryption keys, the sender and receiver are secure even if they do not trust the quantum repeater. Any other application of a quantum internet also requires the end to end transmission of qubits, and thus a quantum repeater.

Quantum repeaters allow entanglement and can be established at distant nodes without physically sending an entangled qubit the entire distance.

In this case, the quantum network consists of many short distance links of perhaps tens or hundreds of kilometers. In the simplest case of a single repeater, two pairs of entangled qubits are established: ${\displaystyle |A\rangle }$ and ${\displaystyle |R_{a}\rangle }$ located at the sender and the repeater, and a second pair ${\displaystyle |R_{b}\rangle }$ and ${\displaystyle |B\rangle }$ located at the repeater and the receiver. These initial entangled qubits can be easily created, for example through parametric down conversion, with one qubit physically transmitted to an adjacent node. At this point, the repeater can perform a bell measurement on the qubits ${\displaystyle |R_{a}\rangle }$ and ${\displaystyle |R_{b}\rangle }$ thus teleporting the quantum state of ${\displaystyle |R_{a}\rangle }$ onto ${\displaystyle |B\rangle }$. This has the effect of "swapping" the entanglement such that ${\displaystyle |A\rangle }$ and ${\displaystyle |B\rangle }$ are now entangled at a distance twice that of the initial entangled pairs. It can be seen that a network of such repeaters can be used linearly or in a hierarchical fashion to establish entanglement over great distances.

Hardware platforms suitable as end nodes above can also function as quantum repeaters. However, there are also hardware platforms specific only to the task of acting as a repeater, without the capabilities of performing quantum gates.

Error correction

Error correction can be used in quantum repeaters. Due to technological limitations, however, the applicability is limited to very short distances as quantum error correction schemes capable of protecting qubits over long distances would require an extremely large amount of qubits and hence extremely large quantum computers.

Errors in communication can be broadly classified into two types: Loss errors (due to optical fiber/environment) and operation errors (such as depolarization, dephasing etc.). While redundancy can be used to detect and correct classical errors, redundant qubits cannot be created due to the no-cloning theorem. As a result, other types of error correction must be introduced such as the Shor code or one of a number of more general and efficient codes. All of these codes work by distributing the quantum information across multiple entangled qubits so that operation errors as well as loss errors can be corrected.

In addition to quantum error correction, classical error correction can be employed by quantum networks in special cases such as quantum key distribution. In these cases, the goal of the quantum communication is to securely transmit a string of classical bits. Traditional error correction codes such as Hamming codes can be applied to the bit string before encoding and transmission on the quantum network.

Entanglement purification

Quantum decoherence can occur when one qubit from a maximally entangled bell state is transmitted across a quantum network. Entanglement purification allows for the creation of nearly maximally entangled qubits from a large number of arbitrary weakly entangled qubits, and thus provides additional protection against errors. Entanglement purification (also known as Entanglement distillation) has already been demonstrated in Nitrogen-vacancy centers in diamond.

Applications

A quantum internet supports numerous applications, enabled by quantum entanglement. In general, quantum entanglement is well suited for tasks that require coordination, synchronization or privacy.

Examples of such applications include quantum key distribution, clock synchronization, protocols for distributed system problems such as leader election or byzantine agreement, extending the baseline of telescopes, as well as position verification, secure identification and two-party cryptography in the noisy-storage model. A quantum internet also enables secure access to a quantum computer in the cloud. Specifically, a quantum internet enables very simple quantum devices to connect to a remote quantum computer in such a way that computations can be performed there without the quantum computer finding out what this computation actually is (the input and output quantum states can not be measured without destroying the computation, but the circuit composition used for the calculation will be known).

Secure communications

When it comes to communicating in any form the largest issue has always been keeping your communications private. From when couriers were used to send letters between ancient battle commanders to secure radio communications that exist today the main purpose is to ensure that what a sender sends out to the receiver reaches the receiver unmolested. This is an area in which Quantum Networks particularly excel. By applying a quantum operator that the user selects to a system of information the information can then be sent to the receiver without a chance of an eavesdropper being able to accurately be able to record the sent information without either the sender or receiver knowing. This works because if a listener tries to listen in then they will change the information in an unintended way by listening thereby tipping their hand to the people on whom they are attacking. Secondly, without the proper quantum operator to decode the information they will corrupt the sent information without being able to use it themselves.

Current status

Quantum internet

At present, there is no network connecting quantum processors, or quantum repeaters deployed outside a lab.

Quantum key distribution networks

Several test networks have been deployed that are tailored to the task of quantum key distribution either at short distances (but connecting many users), or over larger distances by relying on trusted repeaters. These networks do not yet allow for the end to end transmission of qubits or the end to end creation of entanglement between far away nodes.

Major quantum network projects and QKD protocols implemented

Quantum network	Start	BB84	BBM92	E91	DPS	COW
DARPA Quantum Network	2001	Yes	No	No	No	No
Geneva area network (SwissQuantum)	2010	Yes	No	No	No	Yes
Hierarchical network in Wuhu, China	2009	Yes	No	No	No	No
SECOCQ QKD network in Vienna	2003	Yes	Yes	No	No	Yes
Tokyo QKD network	2009	Yes	Yes	No	Yes	No

DARPA Quantum Network

Starting in the early 2000s, DARPA began sponsorship of a quantum network development project with the aim of implementing secure communication. The DARPA Quantum Network became operational within the BBN Technologies laboratory in late 2003 and was expanded further in 2004 to include nodes at Harvard and Boston Universities. The network consists of multiple physical layers including fiber optics supporting phase-modulated lasers and entangled photons as well free-space links.

SECOQC Vienna QKD network

From 2003 to 2008 the Secure Communication based on Quantum Cryptography (SECOQC) project developed a collaborative network between a number of European institutions. The architecture chosen for the SECOQC project is a trusted repeater architecture which consists of point-to-point quantum links between devices where long distance communication is accomplished through the use of repeaters.

Chinese hierarchical network

In May 2009, a hierarchical quantum network was demonstrated in Wuhu, China. The hierarchical network consists of a backbone network of four nodes connecting a number of subnets. The backbone nodes are connected through an optical switching quantum router. Nodes within each subnet are also connected through an optical switch and are connected to the backbone network through a trusted relay.

Geneva area network (SwissQuantum)

The SwissQuantum network developed and tested between 2009 and 2011 linked facilities at CERN with the University of Geneva and hepia in Geneva. The SwissQuantum program focused on transitioning the technologies developed in the SECOQC and other research quantum networks into a production environment. In particular the integration with existing telecommunication networks, and its reliability and robustness.

Tokyo QKD network

In 2010, a number of organizations from Japan and the European Union setup and tested the Tokyo QKD network. The Tokyo network build upon existing QKD technologies and adopted a SECOQC like network architecture. For the first time, one-time-pad encryption was implemented at high enough data rates to support popular end-user application such as secure voice and video conferencing. Previous large-scale QKD networks typically used classical encryption algorithms such as AES for high-rate data transfer and use the quantum-derived keys for low rate data or for regularly re-keying the classical encryption algorithms.

Beijing-Shanghai Trunk Line

In September 2017, a 2000-km quantum key distribution network between Beijing and Shanghai, China, was officially opened. This trunk line will serve as a backbone connecting quantum networks in Beijing, Shanghai, Jinan in Shandong province and Hefei in Anhui province. During the opening ceremony, two employees from the Bank of Communications completed a transaction from Shanghai to Beijing using the network. The State Grid Corporation of China is also developing a managing application for the link. The line uses 32 trusted nodes as repeaters. A quantum telecommunication network has been also put into service in Wuhan, capital of central China's Hubei Province, which will be connected to the trunk. Other similar city quantum networks along the Yangtze River are planned to follow.^[

Quantum machine learning

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Quantum_machine_learning 

Quantum machine learning is an emerging interdisciplinary research area at the intersection of quantum physics and machine learning. The most common use of the term refers to machine learning algorithms for the analysis of classical data executed on a quantum computer, i.e. quantum-enhanced machine learning. While machine learning algorithms are used to compute immense quantities of data, quantum machine learning increases such capabilities intelligently, by creating opportunities to conduct analysis on quantum states and systems. This includes hybrid methods that involve both classical and quantum processing, where computationally difficult subroutines are outsourced to a quantum device. 

These routines can be more complex in nature and executed faster with the assistance of quantum devices. Furthermore, quantum algorithms can be used to analyze quantum states instead of classical data. Beyond quantum computing, the term "quantum machine learning" is often associated with classical machine learning methods applied to data generated from quantum experiments (i.e. machine learning of quantum systems), such as learning quantum phase transitions or creating new quantum experiments. Quantum machine learning also extends to a branch of research that explores methodological and structural similarities between certain physical systems and learning systems, in particular neural networks. For example, some mathematical and numerical techniques from quantum physics are applicable to classical deep learning and vice versa. Finally, researchers investigate more abstract notions of learning theory with respect to quantum information, sometimes referred to as "quantum learning theory".

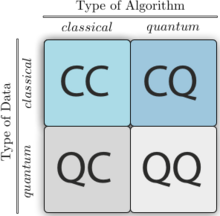
Four different approaches to combine the disciplines of quantum computing and machine learning. The first letter refers to whether the system under study is classical or quantum, while the second letter defines whether a classical or quantum information processing device is used.

Machine learning with quantum computers

Quantum-enhanced machine learning refers to quantum algorithms that solve tasks in machine learning, thereby improving and often expediting classical machine learning techniques. Such algorithms typically require one to encode the given classical data set into a quantum computer to make it accessible for quantum information processing. Subsequently, quantum information processing routines are applied and the result of the quantum computation is read out by measuring the quantum system. For example, the outcome of the measurement of a qubit reveals the result of a binary classification task. While many proposals of quantum machine learning algorithms are still purely theoretical and require a full-scale universal quantum computer to be tested, others have been implemented on small-scale or special purpose quantum devices.

Linear algebra simulation with quantum amplitudes

A number of quantum algorithms for machine learning are based on the idea of amplitude encoding, that is, to associate the amplitudes of a quantum state with the inputs and outputs of computations.

Since a state of ${\displaystyle n}$ qubits is described by ${\displaystyle 2^{n}}$ complex amplitudes, this information encoding can allow for an exponentially compact representation. Intuitively, this corresponds to associating a discrete probability distribution over binary random variables with a classical vector. The goal of algorithms based on amplitude encoding is to formulate quantum algorithms whose resources grow polynomially in the number of qubits ${\displaystyle n}$, which amounts to a logarithmic growth in the number of amplitudes and thereby the dimension of the input.

Many quantum machine learning algorithms in this category are based on variations of the quantum algorithm for linear systems of equations (colloquially called HHL, after the paper's authors) which, under specific conditions, performs a matrix inversion using an amount of physical resources growing only logarithmically in the dimensions of the matrix. One of these conditions is that a Hamiltonian which entrywise corresponds to the matrix can be simulated efficiently, which is known to be possible if the matrix is sparse or low rank. For reference, any known classical algorithm for matrix inversion requires a number of operations that grows at least quadratically in the dimension of the matrix.

Quantum matrix inversion can be applied to machine learning methods in which the training reduces to solving a linear system of equations, for example in least-squares linear regression, the least-squares version of support vector machines, and Gaussian processes.

A crucial bottleneck of methods that simulate linear algebra computations with the amplitudes of quantum states is state preparation, which often requires one to initialise a quantum system in a state whose amplitudes reflect the features of the entire dataset. Although efficient methods for state preparation are known for specific cases, this step easily hides the complexity of the task.

Quantum machine learning algorithms based on Grover search

Another approach to improving classical machine learning with quantum information processing uses amplitude amplification methods based on Grover's search algorithm, which has been shown to solve unstructured search problems with a quadratic speedup compared to classical algorithms. These quantum routines can be employed for learning algorithms that translate into an unstructured search task, as can be done, for instance, in the case of the k-medians and the k-nearest neighbors algorithms. Another application is a quadratic speedup in the training of perceptron.

Amplitude amplification is often combined with quantum walks to achieve the same quadratic speedup. Quantum walks have been proposed to enhance Google's PageRank algorithm as well as the performance of reinforcement learning agents in the projective simulation framework.

Quantum-enhanced reinforcement learning

Reinforcement learning is a branch of machine learning distinct from supervised and unsupervised learning, which also admits quantum enhancements. In quantum-enhanced reinforcement learning, a quantum agent interacts with a classical environment and occasionally receives rewards for its actions, which allows the agent to adapt its behavior—in other words, to learn what to do in order to gain more rewards. In some situations, either because of the quantum processing capability of the agent, or due to the possibility to probe the environment in superpositions, a quantum speedup may be achieved. Implementations of these kinds of protocols in superconducting circuits and in systems of trapped ions have been proposed.

Quantum annealing

Quantum annealing is an optimization technique used to determine the local minima and maxima of a function over a given set of candidate functions. This is a method of discretizing a function with many local minima or maxima in order to determine the observables of the function. The process can be distinguished from Simulated annealing by the Quantum tunneling process, by which particles tunnel through kinetic or potential barriers from a high state to a low state. Quantum annealing starts from a superposition of all possible states of a system, weighted equally. Then the time-dependent Schrödinger equation guides the time evolution of the system, serving to affect the amplitude of each state as time increases. Eventually, the ground state can be reached to yield the instantaneous Hamiltonian of the system.

Quantum sampling techniques

Sampling from high-dimensional probability distributions is at the core of a wide spectrum of computational techniques with important applications across science, engineering, and society. Examples include deep learning, probabilistic programming, and other machine learning and artificial intelligence applications.

A computationally hard problem, which is key for some relevant machine learning tasks, is the estimation of averages over probabilistic models defined in terms of a Boltzmann distribution. Sampling from generic probabilistic models is hard: algorithms relying heavily on sampling are expected to remain intractable no matter how large and powerful classical computing resources become. Even though quantum annealers, like those produced by D-Wave Systems, were designed for challenging combinatorial optimization problems, it has been recently recognized as a potential candidate to speed up computations that rely on sampling by exploiting quantum effects.

Some research groups have recently explored the use of quantum annealing hardware for training Boltzmann machines and deep neural networks. The standard approach to training Boltzmann machines relies on the computation of certain averages that can be estimated by standard sampling techniques, such as Markov chain Monte Carlo algorithms. Another possibility is to rely on a physical process, like quantum annealing, that naturally generates samples from a Boltzmann distribution. The objective is to find the optimal control parameters that best represent the empirical distribution of a given dataset.

The D-Wave 2X system hosted at NASA Ames Research Center has been recently used for the learning of a special class of restricted Boltzmann machines that can serve as a building block for deep learning architectures. Complementary work that appeared roughly simultaneously showed that quantum annealing can be used for supervised learning in classification tasks. The same device was later used to train a fully connected Boltzmann machine to generate, reconstruct, and classify down-scaled, low-resolution handwritten digits, among other synthetic datasets. In both cases, the models trained by quantum annealing had a similar or better performance in terms of quality. The ultimate question that drives this endeavour is whether there is quantum speedup in sampling applications. Experience with the use of quantum annealers for combinatorial optimization suggests the answer is not straightforward.

Inspired by the success of Boltzmann machines based on classical Boltzmann distribution, a new machine learning approach based on quantum Boltzmann distribution of a transverse-field Ising Hamiltonian was recently proposed. Due to the non-commutative nature of quantum mechanics, the training process of the quantum Boltzmann machine can become nontrivial. This problem was, to some extent, circumvented by introducing bounds on the quantum probabilities, allowing the authors to train the model efficiently by sampling. It is possible that a specific type of quantum Boltzmann machine has been trained in the D-Wave 2X by using a learning rule analogous to that of classical Boltzmann machines.

Quantum annealing is not the only technology for sampling. In a prepare-and-measure scenario, a universal quantum computer prepares a thermal state, which is then sampled by measurements. This can reduce the time required to train a deep restricted Boltzmann machine, and provide a richer and more comprehensive framework for deep learning than classical computing. The same quantum methods also permit efficient training of full Boltzmann machines and multi-layer, fully connected models and do not have well-known classical counterparts. Relying on an efficient thermal state preparation protocol starting from an arbitrary state, quantum-enhanced Markov logic networks exploit the symmetries and the locality structure of the probabilistic graphical model generated by a first-order logic template. This provides an exponential reduction in computational complexity in probabilistic inference, and, while the protocol relies on a universal quantum computer, under mild assumptions it can be embedded on contemporary quantum annealing hardware.

Quantum neural networks

Quantum analogues or generalizations of classical neural nets are often referred to as quantum neural networks. The term is claimed by a wide range of approaches, including the implementation and extension of neural networks using photons, layered variational circuits or quantum Ising-type models. Quantum neural networks are often defined as an expansion on Deutsch's model of a quantum computational network. Within this model, nonlinear and irreversible gates, dissimilar to the Hamiltonian operator, are deployed to speculate the given data set. Such gates make certain phases unable to be observed and generate specific oscillations. Quantum neural networks apply the principals quantum information and quantum computation to classical neurocomputing. Current research shows that QNN can exponentially increase the amount of computing power and the degrees of freedom for a computer, which is limited for a classical computer to its size. A quantum neural network has computational capabilities to decrease the number of steps, qubits used, and computation time. The wave function to quantum mechanics is the neuron for Neural networks. To test quantum applications in a neural network, quantum dot molecules are deposited on a substrate of GaAs or similar to record how they communicate with one another. Each quantum dot can be referred as an island of electric activity, and when such dots are close enough (approximately 10±20 nm) electrons can tunnel underneath the islands. An even distribution across the substrate in sets of two create dipoles and ultimately two spin states, up or down. These states are commonly known as qubits with corresponding states of ${\displaystyle |0\rangle }$ and ${\displaystyle |1\rangle }$ in Dirac notation.

Hidden Quantum Markov Models

Hidden Quantum Markov Models (HQMMs) are a quantum-enhanced version of classical Hidden Markov Models (HMMs), which are typically used to model sequential data in various fields like robotics and natural language processing. Unlike the approach taken by other quantum-enhanced machine learning algorithms, HQMMs can be viewed as models inspired by quantum mechanics that can be run on classical computers as well. Where classical HMMs use probability vectors to represent hidden 'belief' states, HQMMs use the quantum analogue: density matrices. Recent work has shown that these models can be successfully learned by maximizing the log-likelihood of the given data via classical optimization, and there is some empirical evidence that these models can better model sequential data compared to classical HMMs in practice, although further work is needed to determine exactly when and how these benefits are derived. Additionally, since classical HMMs are a particular kind of Bayes net, an exciting aspect of HQMMs is that the techniques used show how we can perform quantum-analogous Bayesian inference, which should allow for the general construction of the quantum versions of probabilistic graphical models.

Fully quantum machine learning

In the most general case of quantum machine learning, both the learning device and the system under study, as well as their interaction, are fully quantum. This section gives a few examples of results on this topic.

One class of problem that can benefit from the fully quantum approach is that of 'learning' unknown quantum states, processes or measurements, in the sense that one can subsequently reproduce them on another quantum system. For example, one may wish to learn a measurement that discriminates between two coherent states, given not a classical description of the states to be discriminated, but instead a set of example quantum systems prepared in these states. The naive approach would be to first extract a classical description of the states and then implement an ideal discriminating measurement based on this information. This would only require classical learning. However, one can show that a fully quantum approach is strictly superior in this case. (This also relates to work on quantum pattern matching.) The problem of learning unitary transformations can be approached in a similar way.

Going beyond the specific problem of learning states and transformations, the task of clustering also admits a fully quantum version, wherein both the oracle which returns the distance between data-points and the information processing device which runs the algorithm are quantum. Finally, a general framework spanning supervised, unsupervised and reinforcement learning in the fully quantum setting was introduced in, where it was also shown that the possibility of probing the environment in superpositions permits a quantum speedup in reinforcement learning.

Classical learning applied to quantum problems

The term "quantum machine learning" sometimes refers to classical machine learning performed on data from quantum systems. A basic example of this is quantum state tomography, where a quantum state is learned from measurement. Other applications include learning Hamiltonians and automatically generating quantum experiments.

Quantum learning theory

Quantum learning theory pursues a mathematical analysis of the quantum generalizations of classical learning models and of the possible speed-ups or other improvements that they may provide. The framework is very similar to that of classical computational learning theory, but the learner in this case is a quantum information processing device, while the data may be either classical or quantum. Quantum learning theory should be contrasted with the quantum-enhanced machine learning discussed above, where the goal was to consider specific problems and to use quantum protocols to improve the time complexity of classical algorithms for these problems. Although quantum learning theory is still under development, partial results in this direction have been obtained.

The starting point in learning theory is typically a concept class, a set of possible concepts. Usually a concept is a function on some domain, such as ${\displaystyle \{0,1\}^{n}}$. For example, the concept class could be the set of disjunctive normal form (DNF) formulas on n bits or the set of Boolean circuits of some constant depth. The goal for the learner is to learn (exactly or approximately) an unknown target concept from this concept class. The learner may be actively interacting with the target concept, or passively receiving samples from it.

In active learning, a learner can make membership queries to the target concept c, asking for its value c(x) on inputs x chosen by the learner. The learner then has to reconstruct the exact target concept, with high probability. In the model of quantum exact learning, the learner can make membership queries in quantum superposition. If the complexity of the learner is measured by the number of membership queries it makes, then quantum exact learners can be polynomially more efficient than classical learners for some concept classes, but not more. If complexity is measured by the amount of time the learner uses, then there are concept classes that can be learned efficiently by quantum learners but not by classical learners (under plausible complexity-theoretic assumptions).

A natural model of passive learning is Valiant's probably approximately correct (PAC) learning. Here the learner receives random examples (x,c(x)), where x is distributed according to some unknown distribution D. The learner's goal is to output a hypothesis function h such that h(x)=c(x) with high probability when x is drawn according to D. The learner has to be able to produce such an 'approximately correct' h for every D and every target concept c in its concept class. We can consider replacing the random examples by potentially more powerful quantum examples ${\displaystyle \sum _{x}{\sqrt {D(x)}}|x,c(x)\rangle }$. In the PAC model (and the related agnostic model), this doesn't significantly reduce the number of examples needed: for every concept class, classical and quantum sample complexity are the same up to constant factors. However, for learning under some fixed distribution D, quantum examples can be very helpful, for example for learning DNF under the uniform distribution. When considering time complexity, there exist concept classes that can be PAC-learned efficiently by quantum learners, even from classical examples, but not by classical learners (again, under plausible complexity-theoretic assumptions).

This passive learning type is also the most common scheme in supervised learning: a learning algorithm typically takes the training examples fixed, without the ability to query the label of unlabelled examples. Outputting a hypothesis h is a step of induction. Classically, an inductive model splits into a training and an application phase: the model parameters are estimated in the training phase, and the learned model is applied an arbitrary many times in the application phase. In the asymptotic limit of the number of applications, this splitting of phases is also present with quantum resources.

Implementations and experiments

The earliest experiments were conducted using the adiabatic D-Wave quantum computer, for instance, to detect cars in digital images using regularized boosting with a nonconvex objective function in a demonstration in 2009. Many experiments followed on the same architecture, and leading tech companies have shown interest in the potential of quantum machine learning for future technological implementations. In 2013, Google Research, NASA, and the Universities Space Research Association launched the Quantum Artificial Intelligence Lab which explores the use of the adiabatic D-Wave quantum computer. A more recent example trained a probabilistic generative models with arbitrary pairwise connectivity, showing that their model is capable of generating handwritten digits as well as reconstructing noisy images of bars and stripes and handwritten digits.

Using a different annealing technology based on nuclear magnetic resonance (NMR), a quantum Hopfield network was implemented in 2009 that mapped the input data and memorized data to Hamiltonians, allowing the use of adiabatic quantum computation. NMR technology also enables universal quantum computing, and it was used for the first experimental implementation of a quantum support vector machine to distinguish hand written number ‘6’ and ‘9’ on a liquid-state quantum computer in 2015. The training data involved the pre-processing of the image which maps them to normalized 2-dimensional vectors to represent the images as the states of a qubit. The two entries of the vector are the vertical and horizontal ratio of the pixel intensity of the image. Once the vectors are defined on the feature space, the quantum support vector machine was implemented to classify the unknown input vector. The readout avoids costly quantum tomography by reading out the final state in terms of direction (up/down) of the NMR signal.

Photonic implementations are attracting more attention, not the least because they do not require extensive cooling. Simultaneous spoken digit and speaker recognition and chaotic time-series prediction were demonstrated at data rates beyond 1 gigabyte per second in 2013. Using non-linear photonics to implement an all-optical linear classifier, a perceptron model was capable of learning the classification boundary iteratively from training data through a feedback rule. A core building block in many learning algorithms is to calculate the distance between two vectors: this was first experimentally demonstrated for up to eight dimensions using entangled qubits in a photonic quantum computer in 2015.

Recently, based on a neuromimetic approach, a novel ingredient has been added to the field of quantum machine learning, in the form of a so-called quantum memristor, a quantized model of the standard classical memristor. This device can be constructed by means of a tunable resistor, weak measurements on the system, and a classical feed-forward mechanism. An implementation of a quantum memristor in superconducting circuits has been proposed, and an experiment with quantum dots performed. A quantum memristor would implement nonlinear interactions in the quantum dynamics which would aid the search for a fully functional quantum neural network.

Since 2016, IBM has launched an online cloud-based platform for quantum software developers, called the IBM Q Experience. This platform consists of several fully operational quantum processors accessible via the IBM Web API. In doing so, the company is encouraging software developers to pursue new algorithms through a development environment with quantum capabilities. New architectures are being explored on an experimental basis, up to 32 qbits, utilizing both trapped-ion and superconductive quantum computing methods.

In October 2019, it was noted that the introduction of Quantum Random Number Generators (QRNGs) to machine learning models including Neural Networks and Convolutional Neural Networks for random initial weight distribution and Random Forests for splitting processes had a profound effect on their ability when compared to the classical method of Pseudorandom Number Generators (PRNGs).