Insect flight

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Insect_flight 

 

A tau emerald (Hemicordulia tau) dragonfly has flight muscles attached directly to its wings.

Insects are the only group of invertebrates that have evolved wings and flight. Insects first flew in the Carboniferous, some 350 to 400 million years ago, making them the first animals to evolve flight. Wings may have evolved from appendages on the sides of existing limbs, which already had nerves, joints, and muscles used for other purposes. These may initially have been used for sailing on water, or to slow the rate of descent when gliding.

Two insect groups, the dragonflies and mayflies, have flight muscles attached directly to the wings. In other winged insects, flight muscles attach to the thorax, which make it oscillate in order to induce the wings to beat. Of these insects, some (flies and some beetles) achieve very high wingbeat frequencies through the evolution of an "asynchronous" nervous system, in which the thorax oscillates faster than the rate of nerve impulses.

Not all insects are capable of flight. A number of apterous insects have secondarily lost their wings through evolution, while other more basal insects like silverfish never evolved wings. In some eusocial insects like ants and termites, only the alate reproductive castes develop wings during the mating season before shedding their wings after mating, while the members of other castes are wingless their entire lives.

Some very small insects make use not of steady-state aerodynamics, but of the Weis-Fogh clap and fling mechanism, generating large lift forces at the expense of wear and tear on the wings. Many insects can hover, maintaining height and controlling their position. Some insects such as moths have the forewings coupled to the hindwings so these can work in unison.

Mechanisms

Direct flight

Unlike other insects, the wing muscles of the Ephemeroptera (mayflies) and Odonata (dragonflies and damselflies) insert directly at the wing bases, which are hinged so that a small downward movement of the wing base lifts the wing itself upward, much like rowing through the air. Dragonflies and damselflies have fore and hind wings similar in shape and size. Each operates independently, which gives a degree of fine control and mobility in terms of the abruptness with which they can change direction and speed, not seen in other flying insects. Odonates are all aerial predators, and they have always hunted other airborne insects.

• 

  Direct flight: muscles attached to wings. Large insects only

• 

  The Odonata (dragonflies and damselflies) have direct flight musculature, as do mayflies.

Indirect flight

Other than the two orders with direct flight muscles, all other living winged insects fly using a different mechanism, involving indirect flight muscles. This mechanism evolved once and is the defining feature (synapomorphy) for the infraclass Neoptera; it corresponds, probably not coincidentally, with the appearance of a wing-folding mechanism, which allows Neopteran insects to fold the wings back over the abdomen when at rest (though this ability has been lost secondarily in some groups, such as in the butterflies).

What all Neoptera share, however, is the way the muscles in the thorax work: these muscles, rather than attaching to the wings, attach to the thorax and deform it; since the wings are extensions of the thoracic exoskeleton, the deformations of the thorax cause the wings to move as well. A set of longitudinal muscles along the back compresses the thorax from front to back, causing the dorsal surface of the thorax (notum) to bow upward, making the wings flip down. Another set of muscles from the tergum to the sternum pulls the notum downward again, causing the wings to flip upward.

• 

  Indirect flight: muscles make thorax oscillate in most insects

• 

  The Neoptera, including butterflies and most other insects, have indirect flight musculature

Insects that beat their wings fewer than one hundred times a second use synchronous muscle. Synchronous muscle is a type of muscle that contracts once for every nerve impulse. This generally produces less power and is less efficient than asynchronous muscle, which accounts for the independent evolution of asynchronous flight muscles in several separate insect clades.

Insects that beat their wings more rapidly, such as the bumblebee, use asynchronous muscle; this is a type of muscle that contracts more than once per nerve impulse. This is achieved by the muscle being stimulated to contract again by a release in tension in the muscle, which can happen more rapidly than through simple nerve stimulation alone. This allows the frequency of wing beats to exceed the rate at which the nervous system can send impulses. The asynchronous muscle is one of the final refinements that has appeared in some of the higher Neoptera (Coleoptera, Diptera, and Hymenoptera). The overall effect is that many higher Neoptera can beat their wings much faster than insects with direct flight muscles.

Aerodynamics

Further information: Aerodynamics

There are two basic aerodynamic models of insect flight: creating a leading edge vortex, and using clap and fling.

Leading edge vortex

Most insects use a method that creates a spiralling leading edge vortex. These flapping wings move through two basic half-strokes. The downstroke starts up and back and is plunged downward and forward. Then the wing is quickly flipped over (supination) so that the leading edge is pointed backward. The upstroke then pushes the wing upward and backward. Then the wing is flipped again (pronation) and another downstroke can occur. The frequency range in insects with synchronous flight muscles typically is 5 to 200 hertz (Hz). In those with asynchronous flight muscles, wing beat frequency may exceed 1000 Hz. When the insect is hovering, the two strokes take the same amount of time. A slower downstroke, however, provides thrust.

Identification of major forces is critical to understanding insect flight. The first attempts to understand flapping wings assumed a quasi-steady state. This means that the air flow over the wing at any given time was assumed to be the same as how the flow would be over a non-flapping, steady-state wing at the same angle of attack. By dividing the flapping wing into a large number of motionless positions and then analyzing each position, it would be possible to create a timeline of the instantaneous forces on the wing at every moment. The calculated lift was found to be too small by a factor of three, so researchers realized that there must be unsteady phenomena providing aerodynamic forces. There were several developing analytical models attempting to approximate flow close to a flapping wing. Some researchers predicted force peaks at supination. With a dynamically scaled model of a fruit fly, these predicted forces later were confirmed. Others argued that the force peaks during supination and pronation are caused by an unknown rotational effect that fundamentally is different from the translational phenomena. There is some disagreement with this argument. Through computational fluid dynamics, some researchers argue that there is no rotational effect. They claim that the high forces are caused by an interaction with the wake shed by the previous stroke.

Similar to the rotational effect mentioned above, the phenomena associated with flapping wings are not completely understood or agreed upon. Because every model is an approximation, different models leave out effects that are presumed to be negligible. For example, the Wagner effect, as proposed by Herbert A. Wagner in 1925, says that circulation rises slowly to its steady-state due to viscosity when an inclined wing is accelerated from rest. This phenomenon would explain a lift value that is less than what is predicted. Typically, the case has been to find sources for the added lift. It has been argued that this effect is negligible for flow with a Reynolds number that is typical of insect flight. The Reynolds number is a measure of turbulence; flow is laminar (smooth) when the Reynolds number is low, and turbulent when it is high. The Wagner effect was ignored, consciously, in at least one model. One of the most important phenomena that occurs during insect flight is leading edge suction. This force is significant to the calculation of efficiency. The concept of leading edge suction first was put forth by D. G. Ellis and J. L. Stollery in 1988 to describe vortex lift on sharp-edged delta wings. At high angles of attack, the flow separates over the leading edge, but reattaches before reaching the trailing edge. Within this bubble of separated flow is a vortex. Because the angle of attack is so high, a lot of momentum is transferred downward into the flow. These two features create a large amount of lift force as well as some additional drag. The important feature, however, is the lift. Because the flow has separated, yet it still provides large amounts of lift, this phenomenon is called stall delay, first noticed on aircraft propellers by H. Himmelskamp in 1945. This effect was observed in flapping insect flight and it was proven to be capable of providing enough lift to account for the deficiency in the quasi-steady-state models. This effect is used by canoeists in a sculling draw stroke.

All of the effects on a flapping wing may be reduced to three major sources of aerodynamic phenomena: the leading edge vortex, the steady-state aerodynamic forces on the wing, and the wing’s contact with its wake from previous strokes. The size of flying insects ranges from about 20 micrograms to about 3 grams. As insect body mass increases, wing area increases and wing beat frequency decreases. For larger insects, the Reynolds number (Re) may be as high as 10000, where flow is starting to become turbulent. For smaller insects, it may be as low as 10. This means that viscous effects are much more important to the smaller insects.

downstroke

 

upstroke

Another interesting feature of insect flight is the body tilt. As flight speed increases, the insect body tends to tilt nose-down and become more horizontal. This reduces the frontal area and therefore, the body drag. Since drag also increases as forward velocity increases, the insect is making its flight more efficient as this efficiency becomes more necessary. Additionally, by changing the geometric angle of attack on the downstroke, the insect is able to keep its flight at an optimal efficiency through as many manoeuvres as possible. The development of general thrust is relatively small compared with lift forces. Lift forces may be more than three times the insect's weight, while thrust at even the highest speeds may be as low as 20% of the weight. This force is developed primarily through the less powerful upstroke of the flapping motion.

Clap and fling

The feathery wings of a thrips are unsuitable for leading edge vortex flight, but support clap and fling.

 

Clap and fling is used in sea butterflies like Limacina helicina to "fly" through the water.

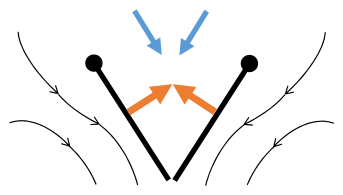
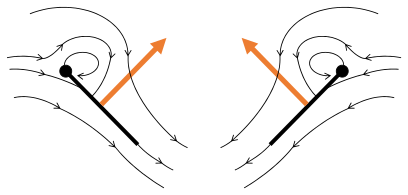
Clap and fling, or the Weis-Fogh mechanism, discovered by the Danish zoologist Torkel Weis-Fogh, is a lift generation method utilized during small insect flight. As insect sizes become less than 1 mm, viscous forces become dominant and the efficacy of lift generation from an airfoil decreases drastically. Starting from the clap position, the two wings fling apart and rotate about the trailing edge. The wings then separate and sweep horizontally until the end of the downstroke. Next, the wings pronate and utilize the leading edge during an upstroke rowing motion. As the clap motion begins, the leading edges meet and rotate together until the gap vanishes. Initially, it was thought that the wings were touching, but several incidents indicate a gap between the wings and suggest it provides an aerodynamic benefit.

Lift generation from the clap and fling mechanism occurs during several processes throughout the motion. First, the mechanism relies on a wing-wing interaction, as a single wing motion does not produce sufficient lift. As the wings rotate about the trailing edge in the flinging motion, air rushes into the created gap and generates a strong leading edge vortex, and a second one developing at the wingtips. A third, weaker, vortex develops on the trailing edge. The strength of the developing vortices relies, in-part, on the initial gap of the inter-wing separation at the start of the flinging motion. With a decreased gap inter-wing gap indicating a larger lift generation, at the cost of larger drag forces. The implementation of a heaving motion during fling, flexible wings, and a delayed stall mechanism were found to reinforce vortex stability and attachment. Finally, to compensate the overall lower lift production during low Reynolds number flight (with laminar flow), tiny insects often have a higher stroke frequency to generate wing-tip velocities that are comparable to larger insects.

The overall largest expected drag forces occur during the dorsal fling motion, as the wings need to separate and rotate. The attenuation of the large drag forces occur through several mechanisms. Flexible wings were found to decrease the drag in flinging motion by up to 50% and further reduce the overall drag through the entire wing stroke when compared to rigid wings. Bristles on the wing edges, as seen in Encarsia formosa, cause a porosity in the flow which augments and reduces the drag forces, at the cost of lower lift generation. Further, the inter-wing separation before fling plays an important role in the overall effect of drag. As the distance increases between the wings, the overall drag decreases.

The clap and fling mechanism is also employed by the marine mollusc Limacina helicina, a sea butterfly. Some insects, such as the vegetable leaf miner Liriomyza sativae (a fly), exploit a partial clap and fling, using the mechanism only on the outer part of the wing to increase lift by some 7% when hovering.

• Clap and fling flight mechanism after Sane 2003
• 

  Clap 1: wings close over back

• 

  Clap 2: leading edges touch, wing rotates around leading edge, vortices form

• 

  Clap 3: trailing edges close, vortices shed, wings close giving thrust

• Black (curved) arrows: flow; Blue arrows: induced velocity; Orange arrows: net force on wing
• 

  Fling 1: wings rotate around trailing edge to fling apart

• 

  Fling 2: leading edge moves away, air rushes in, increasing lift

• 

  Fling 3: new vortex forms at leading edge, trailing edge vortices cancel each other, perhaps helping flow to grow faster (Weis-Fogh 1973)

Governing equations

A wing moving in fluids experiences a fluid force, which follows the conventions found in aerodynamics. The force component normal to the direction of the flow relative to the wing is called lift (L), and the force component in the opposite direction of the flow is drag (D). At the Reynolds numbers considered here, an appropriate force unit is 1/2(ρU²S), where ρ is the density of the fluid, S the wing area, and U the wing speed. The dimensionless forces are called lift (C_L) and drag (C_D) coefficients, that is:

${\displaystyle C_{\text{L}}(\alpha )={\frac {2L}{\rho U^{2}S}}\quad {\text{and}}\quad C_{\text{D}}(\alpha )={\frac {2D}{\rho U^{2}S}}.}$

C_L and C_D are constants only if the flow is steady. A special class of objects such as airfoils may reach a steady state when it slices through the fluid at a small angle of attack. In this case, the inviscid flow around an airfoil can be approximated by a potential flow satisfying the no-penetration boundary condition. The Kutta-Joukowski theorem of a 2D airfoil further assumes that the flow leaves the sharp trailing edge smoothly, and this determines the total circulation around an airfoil. The corresponding lift is given by Bernoulli's principle (Blasius theorem):

${\displaystyle C_{\text{L}}=2\pi \sin \alpha \quad {\text{and}}\quad C_{\text{D}}=0.}$

The flows around birds and insects can be considered incompressible: The Mach number, or velocity relative to the speed of sound in air, is typically 1/300 and the wing frequency is about 10–103 Hz. Using the governing equation as the Navier-Stokes equation being subject to the no-slip boundary condition, the equation is:

${\displaystyle {\begin{aligned}{\frac {\partial \mathbf {u} }{\partial t}}+\left(\mathbf {u} \cdot \nabla \right)\mathbf {u} &=-{\frac {\nabla p}{\rho }}+v\nabla ^{2}\mathbf {u} \\\nabla \cdot \mathbf {u} &=0\\\mathbf {u} _{\text{bd}}&=\mathbf {u} _{\text{s}}.\end{aligned}}}$

Where u(x, t) is the flow field, p the pressure, ρ the density of the fluid, ν the kinematic viscosity, u_bd the velocity at the boundary, and u_s the velocity of the solid. By choosing a length scale, L, and velocity scale, U, the equation can be expressed in nondimensional form containing the Reynolds number, R_e=uL/ν . There are two obvious differences between an insect wing and an airfoil: An insect wing is much smaller and it flaps. Using a dragonfly as an example, Its chord (c) is about 1 cm (0.39 in), its wing length (l) about 4 cm (1.6 in), and its wing frequency (f) about 40 Hz. The tip speed (u) is about 1 m/s (3.3 ft/s), and the corresponding Reynolds number about 103. At the smaller end, a typical chalcidoid wasp has a wing length of about 0.5–0.7 mm (0.020–0.028 in) and beats its wing at about 400 Hz. Its Reynolds number is about 25. The range of Reynolds number in insect flight is about 10 to 10⁴, which lies in between the two limits that are convenient for theories: inviscid steady flows around an airfoil and Stokes flow experienced by a swimming bacterium. For this reason, this intermediate range is not well understood. On the other hand, it is perhaps the most ubiquitous regime among the things we see. Falling leaves and seeds, fishes, and birds all encounter unsteady flows similar to that seen around an insect. The chordwise Reynolds number can be described by:

${\displaystyle Re={\frac {{\bar {c}}U}{v}}}$

${\displaystyle U=2\Theta fr_{g}}$ and ${\displaystyle r_{g}={\sqrt {{\frac {1}{s}}\int _{0}^{R}{r^{2}c(R)dr}}}}$

Where ${\displaystyle {\bar {c}}\ }$ is the average chord length, ${\displaystyle U}$ is the speed of the wing tip, ${\displaystyle \Theta }$ is the stroke amplitude, ${\displaystyle f}$ is the beat frequency, ${\displaystyle r_{g}}$ is the radius of gyration, ${\displaystyle s}$ is the wing area, and ${\displaystyle R}$ is the length of wing, including the wing tip.

In addition to the Reynolds number, there are at least two other relevant dimensionless parameters. A wing has three velocity scales: the flapping velocity with respect to the body (u), the forward velocity of the body (U₀), and the pitching velocity (Ωc). The ratios of them form two dimensionless variables, U₀/u and Ωc/u, the former is often referred to as the advance ratio, and it is also related to the reduced frequency, fc/U₀.

If an insect wing is rigid, for example, a Drosophila wing is approximately so, its motion relative to a fixed body can be described by three variables: the position of the tip in spherical coordinates, (Θ(t),Φ(t)), and the pitching angle ψ(t), about the axis connecting the root and the tip. To estimate the aerodynamic forces based on blade-element analysis, it is also necessary to determine the angle of attack (α). The typical angle of attack at 70% wingspan ranges from 25° to 45° in hovering insects (15° in hummingbirds). Despite the wealth of data available for many insects, relatively few experiments report the time variation of α during a stroke. Among these are wind tunnel experiments of a tethered locust and a tethered fly, and free hovering flight of a fruit fly.

Because they are relatively easy to measure, the wing-tip trajectories have been reported more frequently. For example, selecting only flight sequences that produced enough lift to support a weight, will show that the wing tip follows an elliptical shape. Noncrossing shapes were also reported for other insects. Regardless of their exact shapes, the plugging-down motion indicates that insects may use aerodynamic drag in addition to lift to support its weight.

Hovering

Flight parameters	Speed (m/s)	Beats/s
Aeshnid dragonfly	7.0	38
Hornet	5.7	100
Hummingbird hawkmoth	5.0	85
Horsefly	3.9	96
Hoverfly	3.5	120
Bumblebee	2.9	130
Honeybee	2.5	250
Housefly	2.0	190
Damselfly	1.5	16
Scorpionfly	0.49	28
Large white butterfly	2.5	12
Thrips (clap and fling)	0.3	254

Hoverfly (Xanthogramma pedissequum) has indirect flight musculature.

Many insects can hover, or stay in one spot in the air, doing so by beating their wings rapidly. Doing so requires sideways stabilization as well as the production of lift. The lifting force is mainly produced by the downstroke. As the wings push down on the surrounding air, the resulting reaction force of the air on the wings pushes the insect up. The wings of most insects are evolved so that, during the upward stroke, the force on the wing is small. Since the downbeat and return stroke force the insect up and down respectively, the insect oscillates and winds up staying in the same position.

The distance the insect falls between wingbeats depends on how rapidly its wings are beating: the slower it flaps, the longer the interval in which it falls, and the farther it falls between each wingbeat. One can calculate the wingbeat frequency necessary for the insect to maintain a given stability in its amplitude. To simplify the calculations, one must assume that the lifting force is at a finite constant value while the wings are moving down and that it is zero while the wings are moving up. During the time interval Δt of the upward wingbeat, the insect drops a distance h under the influence of gravity.

${\displaystyle h={\frac {g(\Delta t^{2})}{2}}}$

The upward stroke then restores the insect to its original position. Typically, it may be required that the vertical position of the insect changes by no more than 0.1 mm (i.e., h = 0.1 mm). The maximum allowable time for free fall is then 

${\displaystyle \Delta t=\left({\frac {2h}{g}}\right)^{1/2}={\sqrt {\frac {2\times 10^{-2}{\text{ cm}}}{980{\text{ cm}}/{\text{s}}^{2}}}}\approx 4.5\times 10^{-3}{\text{ s}}}$

Since the up movements and the down movements of the wings are about equal in duration, the period T for a complete up-and-down wing is twice Δr, that is,

${\displaystyle T=2\,\Delta t=9\times 10^{-3}{\text{ s}}}$

The frequency of the beats, f, meaning the number of wingbeats per second, is represented by the equation:

${\displaystyle f={\frac {1}{T}}\approx 110{\text{ s}}^{-1}}$

In the examples used the frequency used is 110 beats/s, which is the typical frequency found in insects. Butterflies have a much slower frequency with about 10 beats/s, which means that they can't hover. Other insects may be able to produce a frequency of 1000 beats/s. To restore the insect to its original vertical position, the average upward force during the downward stroke, F_av, must be equal to twice the weight of the insect. Note that since the upward force on the insect body is applied only for half the time, the average upward force on the insect is simply its weight.

Power input

One can now compute the power required to maintain hovering by, considering again an insect with mass m 0.1 g, average force, F_av, applied by the two wings during the downward stroke is two times the weight. Because the pressure applied by the wings is uniformly distributed over the total wing area, that means one can assume the force generated by each wing acts through a single point at the midsection of the wings. During the downward stroke, the center of the wings traverses a vertical distance d. The total work done by the insect during each downward stroke is the product of force and distance; that is,

${\displaystyle {\text{Work}}=F_{av}\times d={\text{2W}}_{\text{d}}\,\!}$

If the wings swing through the beat at an angle of 70°, then in the case presented for the insect with 1 cm long wings, d is 0.57 cm. Therefore, the work done during each stroke by the two wings is:

${\displaystyle {\text{Work}}=2\times 0.1\times 980\times 0.57=112{\text{erg}}\,\!}$

The energy is used to raise the insect against gravity. The energy E required to raise the mass of the insect 0.1 mm during each downstroke is:

${\displaystyle {\text{E}}={\text{mgh}}=0.1\times 980\times 10^{-2}=0.98{\text{erg}}\,\!}$

This is a negligible fraction of the total energy expended which clearly, most of the energy is expended in other processes. A more detailed analysis of the problem shows that the work done by the wings is converted primarily into kinetic energy of the air that is accelerated by the downward stroke of the wings. The power is the amount of work done in 1 s; in the insect used as an example, makes 110 downward strokes per second. Therefore, its power output P is, strokes per second, and that means its power output P is:

${\displaystyle {\text{P}}=112{\text{erg}}\times 110{\text{/s}}=1.23\times 10^{4}{\text{erg/s}}=1.23\times 10^{-3}{\text{W}}}$

Power output

In the calculation of the power used in hovering, the examples used neglected the kinetic energy of the moving wings. The wings of insects, light as they are, have a finite mass; therefore, as they move they possess kinetic energy. Because the wings are in rotary motion, the maximum kinetic energy during each wing stroke is:

${\displaystyle KE={\frac {1}{2}}I\omega _{\text{max}}^{2}}$

Here I is the moment of inertia of the wing and ω_max is the maximum angular velocity during the wing stroke. To obtain the moment of inertia for the wing, we will assume that the wing can be approximated by a thin rod pivoted at one end. The moment of inertia for the wing is then:

${\displaystyle I={\frac {m\ell ^{2}}{3}}}$

Where l is the length of the wing (1 cm) and m is the mass of two wings, which may be typically 10⁻³ g. The maximum angular velocity, ω_max, can be calculated from the maximum linear velocity, ν_max, at the center of the wing:

${\displaystyle \omega _{\text{max}}={\frac {v_{\text{max}}}{\ell /2}}}$

During each stroke the center of the wings moves with an average linear velocity ν_av given by the distance d traversed by the center of the wing divided by the duration Δt of the wing stroke. From our previous example, d = 0.57 cm and Δt = 4.5×10⁻³ s. Therefore:

${\displaystyle v_{av}={\frac {d}{\Delta t}}={\frac {0.57}{4.5\times 10^{-3}}}=127{\text{cm/s}}}$

The velocity of the wings is zero both at the beginning and at the end of the wing stroke, meaning the maximum linear velocity is higher than the average velocity. If we assume that the velocity oscillates (sinusoidally) along the wing path, the maximum velocity is twice as high as the average velocity. Therefore, the maximum angular velocity is:

${\displaystyle \omega _{\text{max}}={\frac {254}{\ell /2}}}$

And the kinetic energy therefore is:

${\displaystyle KE={\frac {1}{2}}I\omega _{max}^{2}=\left(10^{-3}{\frac {\ell ^{2}}{3}}\right)\left({\frac {254}{\ell /2}}\right)^{2}=43{\text{ erg}}}$

Since there are two wing strokes (the upstroke and downstroke) in each cycle of the wing movement, the kinetic energy is 2×43 = 86 erg. This is about as much energy as is consumed in hovering itself.

Elasticity

Insects gain kinetic energy, provided by the muscles, when the wings accelerate. When the wings begin to decelerate toward the end of the stroke, this energy must dissipate. During the downstroke, the kinetic energy is dissipated by the muscles themselves and is converted into heat (this heat is sometimes used to maintain core body temperature). Some insects are able to utilize the kinetic energy in the upward movement of the wings to aid in their flight. The wing joints of these insects contain a pad of elastic, rubber-like protein called resilin. During the upstroke of the wing, the resilin is stretched. The kinetic energy of the wing is converted into potential energy in the stretched resilin, which stores the energy much like a spring. When the wing moves down, this energy is released and aids in the downstroke.

Using a few simplifying assumptions, we can calculate the amount of energy stored in the stretched resilin. Although the resilin is bent into a complex shape, the example given shows the calculation as a straight rod of area A and length. Furthermore, we will assume that throughout the stretch the resilin obeys Hooke's law. This is not strictly true as the resilin is stretched by a considerable amount and therefore both the area and Young's modulus change in the process of stretching. The potential energy U stored in the stretched resilin is:

${\displaystyle U={\frac {1}{2}}{\frac {EA\Delta \ell ^{2}}{\ell }}}$

Here E is the Young’s modulus for resilin, which has been measured to be 1.8×10⁷ dyn/cm². Typically in an insect the size of a bee, the volume of the resilin may be equivalent to a cylinder 2×10⁻² cm long and 4×10⁻⁴ cm² in area. In the example given, the length of the resilin rod is increased by 50% when stretched. That is, Δℓ is 10⁻² cm. Therefore, in this case the potential energy stored in the resilin of each wing is:

${\displaystyle U={\frac {1}{2}}{\frac {1.8\times 10^{7}\times 4\times 10^{-4}\times 10^{-4}}{2\times 10^{-2}}}=18\ {\text{erg}}}$

The stored energy in the two wings for a bee-sized insect is 36 erg, which is comparable to the kinetic energy in the upstroke of the wings. Experiments show that as much as 80% of the kinetic energy of the wing may be stored in the resilin.

Wing coupling

Main article: Wing coupling

 

Frenulo-retinacular wing coupling in male and female moths

Some four-winged insect orders, such as the Lepidoptera, have developed morphological wing coupling mechanisms in the imago which render these taxa functionally two-winged. All but the most basal forms exhibit this wing-coupling.

The mechanisms are of three different types - jugal, frenulo-retinacular and amplexiform:

• The more primitive groups have an enlarged lobe-like area near the basal posterior margin, i.e. at the base of the forewing, a jugum, that folds under the hindwing in flight.
• Other groups have a frenulum on the hindwing that hooks under a retinaculum on the forewing.
• In almost all butterflies and in the Bombycoidea (except the Sphingidae), there is no arrangement of frenulum and retinaculum to couple the wings. Instead, an enlarged humeral area of the hindwing is broadly overlapped by the forewing. Despite the absence of a specific mechanical connection, the wings overlap and operate in phase. The power stroke of the forewing pushes down the hindwing in unison. This type of coupling is a variation of frenate type but where the frenulum and retinaculum are completely lost.

Biochemistry

The biochemistry of insect flight has been a focus of considerable study. While many insects use carbohydrates and lipids as the energy source for flight, many beetles and flies use the amino acid proline as their energy source. Some species also use a combination of sources and moths such as Manduca sexta use carbohydrates for pre-flight warm-up.

Sensory Feedback

Insects use sensory feedback to maintain and control flight. Research has demonstrated the role of sensory structures such as antennae, halteres and wings in controlling flight posture, wingbeat amplitude, and wingbeat frequency.

Evolution and adaptation

Reconstruction of a Carboniferous insect, the Palaeodictyopteran Mazothairos

Sometime in the Carboniferous Period, some 350 to 400 million years ago, when there were only two major land masses, insects began flying. Among the oldest winged insect fossils is Delitzschala, a Palaeodictyopteran from the Lower Carboniferous; Rhyniognatha is older, from the Early Devonian, but it is uncertain if it had wings, or indeed was an insect.

How and why insect wings developed is not well understood, largely due to the scarcity of appropriate fossils from the period of their development in the Lower Carboniferous. There have historically been three main theories on the origins of insect flight. The first was that they are modifications of movable abdominal gills, as found on aquatic naiads of mayflies. Phylogenomic analysis suggests that the Polyneoptera, the group of winged insects that includes grasshoppers, evolved from a terrestrial ancestor, making the evolution of wings from gills unlikely. Additional study of the jumping behavior of mayfly larvae has determined that tracheal gills play no role in guiding insect descent, providing further evidence against this evolutionary hypothesis. This leaves two major historic theories: that wings developed from paranotal lobes, extensions of the thoracic terga; or that they arose from modifications of leg segments, which already contained muscles.

Epicoxal (abdominal gill) hypothesis

Mayfly nymph with paired abdominal gills

Numerous entomologists including Landois in 1871, Lubbock in 1873, Graber in 1877, and Osborn in 1905 have suggested that a possible origin for insect wings might have been movable abdominal gills found in many aquatic insects, such as on naiads of mayflies. According to this theory these tracheal gills, which started their way as exits of the respiratory system and over time were modified into locomotive purposes, eventually developed into wings. The tracheal gills are equipped with little winglets that perpetually vibrate and have their own tiny straight muscles.

Paranotal (tergal) hypothesis

The paranotal lobe or tergal (dorsal body wall) hypothesis, proposed by Fritz Müller in 1875 and reworked by G. Crampton in 1916, Jarmila Kulakova-Peck in 1978 and Alexander P. Rasnitsyn in 1981 among others, suggests that the insect's wings developed from paranotal lobes, a preadaptation found in insect fossils that would have assisted stabilization while hopping or falling. In favor of this hypothesis is the tendency of most insects, when startled while climbing on branches, to escape by dropping to the ground. Such lobes would have served as parachutes and enable the insect to land more softly. The theory suggests that these lobes gradually grew larger and in a later stage developed a joint with the thorax. Even later would appear the muscles to move these crude wings. This model implies a progressive increase in the effectiveness of the wings, starting with parachuting, then gliding and finally active flight. Still, lack of substantial fossil evidence of the development of the wing joints and muscles poses a major difficulty to the theory, as does the seemingly spontaneous development of articulation and venation, and it has been largely rejected by experts in the field.

Endite-exite (pleural) hypothesis

Leg of a trilobite, an early arthropod. The internal branch made of endites is at the top; the smaller external branch made of exites is below. Trueman proposed that an endite and an exite fused to form a wing.

In 1990, J. W. H. Trueman proposed that the wing was adapted from endites and exites, appendages on the respective inner and outer aspects of the primitive arthropod limb, also called the pleural hypothesis. This was based on a study by Goldschmidt in 1945 on Drosophila melanogaster, in which a variation called "pod" (for podomeres, limb segments) displayed a mutation that transformed normal wings. The result was interpreted as a triple-jointed leg arrangement with some additional appendages but lacking the tarsus, where the wing's costal surface would normally be. This mutation was reinterpreted as strong evidence for a dorsal exite and endite fusion, rather than a leg, with the appendages fitting in much better with this hypothesis. The innervation, articulation and musculature required for the evolution of wings are already present in the limb segments.

Other hypotheses

Other hypotheses include Vincent Wigglesworth's 1973 suggestion that wings developed from thoracic protrusions used as radiators.

Adrian Thomas and Åke Norberg suggested in 2003 that wings may have evolved initially for sailing on the surface of water as seen in some stoneflies.

Stephen P. Yanoviak and colleagues proposed in 2009 that the wing derives from directed aerial gliding descent—a preflight phenomenon found in some apterygota, a wingless sister taxon to the winged insects.

Dual origin

Biologists including Averof, Niwa, Elias-Neto and their colleagues have begun to explore the origin of the insect wing using evo-devo in addition to palaeontological evidence. This suggests that wings are serially homologous with both tergal and pleural structures, potentially resolving the centuries-old debate. Jakub Prokop and colleagues have in 2017 found palaeontological evidence from Paleozoic nymphal wing pads that wings indeed had such a dual origin.

Quantum foundations

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Quantum_foundations 

Quantum foundations is a discipline of science that seeks to understand the most counter-intuitive aspects of quantum theory, reformulate it and even propose new generalizations thereof. Contrary to other physical theories, such as general relativity, the defining axioms of quantum theory are quite ad hoc, with no obvious physical intuition. While they lead to the right experimental predictions, they do not come with a mental picture of the world where they fit.

There exist different approaches to resolve this conceptual gap:

• First, one can put quantum physics in contraposition with classical physics: by identifying scenarios, such as Bell experiments, where quantum theory radically deviates from classical predictions, one hopes to gain physical insights on the structure of quantum physics.
• Second, one can attempt to find a re-derivation of the quantum formalism in terms of operational axioms.
• Third, one can search for a full correspondence between the mathematical elements of the quantum framework and physical phenomena: any such correspondence is called an interpretation.
• Fourth, one can renounce quantum theory altogether and propose a different model of the world.

Research in quantum foundations is structured along these roads.

Non-classical features of quantum theory

Quantum nonlocality

Main article: Quantum nonlocality

Two or more separate parties conducting measurements over a quantum state can observe correlations which cannot be explained with any local hidden variable theory. Whether this should be regarded as proving that the physical world itself is "nonlocal" is a topic of debate, but the terminology of "quantum nonlocality" is commonplace. Nonlocality research efforts in quantum foundations focus on determining the exact limits that classical or quantum physics enforces on the correlations observed in a Bell experiment or more complex causal scenarios. This research program has so far provided a generalization of Bell's theorem that allows falsifying all classical theories with a superluminal, yet finite, hidden influence.

Quantum contextuality

Main article: Quantum contextuality

Nonlocality can be understood as an instance of quantum contextuality. A situation is contextual when the value of an observable depends on the context in which it is measured (namely, on which other observables are being measured as well). The original definition of measurement contextuality can be extended to state preparations and even general physical transformations.

Epistemic models for the quantum wave-function

A physical property is epistemic when it represents our knowledge or beliefs on the value of a second, more fundamental feature. The probability of an event to occur is an example of an epistemic property. In contrast, a non-epistemic or ontic variable captures the notion of a “real” property of the system under consideration.

There is an on-going debate on whether the wave-function represents the epistemic state of a yet to be discovered ontic variable or, on the contrary, it is a fundamental entity. Under some physical assumptions, the Pusey–Barrett–Rudolph (PBR) theorem demonstrates the inconsistency of quantum states as epistemic states, in the sense above. Note that, in QBism and Copenhagen-type views, quantum states are still regarded as epistemic, not with respect to some ontic variable, but to one's expectations about future experimental outcomes. The PBR theorem does not exclude such epistemic views on quantum states.

Axiomatic reconstructions

Some of the counter-intuitive aspects of quantum theory, as well as the difficulty to extend it, follow from the fact that its defining axioms lack a physical motivation. An active area of research in quantum foundations is therefore to find alternative formulations of quantum theory which rely on physically compelling principles. Those efforts come in two flavors, depending on the desired level of description of the theory: the so-called Generalized Probabilistic Theories approach and the Black boxes approach.

The framework of Generalized Probabilistic Theories

Main article: Generalized probabilistic theories

Generalized Probabilistic Theories (GPTs) are a general framework to describe the operational features of arbitrary physical theories. Essentially, they provide a statistical description of any experiment combining state preparations, transformations and measurements. The framework of GPTs can accommodate classical and quantum physics, as well as hypothetical non-quantum physical theories which nonetheless possess quantum theory's most remarkable features, such as entanglement or teleportation. Notably, a small set of physically motivated axioms is enough to single out the GPT representation of quantum theory.

L. Hardy introduced the concept of GPT in 2001, in an attempt to re-derive quantum theory from basic physical principles. Although Hardy's work was very influential (see the follow-ups below), one of his axioms was regarded as unsatisfactory: it stipulated that, of all the physical theories compatible with the rest of the axioms, one should choose the simplest one. The work of Dakic and Brukner eliminated this “axiom of simplicity” and provided a reconstruction of quantum theory based on three physical principles. This was followed by the more rigorous reconstruction of Masanes and Müller.

Axioms common to these three reconstructions are:

• The subspace axiom: systems which can store the same amount of information are physically equivalent.
• Local tomography: to characterize the state of a composite system it is enough to conduct measurements at each part.
• Reversibility: for any two extremal states [i.e., states which are not statistical mixtures of other states], there exists a reversible physical transformation that maps one into the other.

An alternative GPT reconstruction proposed by Chiribella et al. around the same time is also based on the

• Purification axiom: for any state ${\displaystyle S_{A}}$ of a physical system A there exists a bipartite physical system ${\displaystyle A-B}$ and an extremal state (or purification) ${\displaystyle T_{AB}}$ such that ${\displaystyle S_{A}}$ is the restriction of ${\displaystyle T_{AB}}$ to system ${\displaystyle A}$. In addition, any two such purifications ${\displaystyle T_{AB},T_{AB}^{\prime }}$ of ${\displaystyle S_{A}}$ can be mapped into one another via a reversible physical transformation on system ${\displaystyle B}$.

The use of purification to characterize quantum theory has been criticized on the grounds that it also applies in the Spekkens toy model.

To the success of the GPT approach, it can be countered that all such works just recover finite dimensional quantum theory. In addition, none of the previous axioms can be experimentally falsified unless the measurement apparatuses are assumed to be tomographically complete.

Categorical Quantum Mechanics or Process Theories

Main article: Categorical quantum mechanics

Categorical Quantum Mechanics (CQM) or Process Theories are a general framework to describe physical theories, with an emphasis on processes and their compositions. It was pioneered by Samson Abramsky and Bob Coecke. Besides its influence in quantum foundations, most notably the use of a diagrammatic formalism, CQM also plays an important role in quantum technologies, most notably in the form of ZX-calculus. It also has been used to model theories outside of physics, for example the DisCoCat compositional natural language meaning model.

The framework of black boxes

Main article: Quantum nonlocality

In the black box or device-independent framework, an experiment is regarded as a black box where the experimentalist introduces an input (the type of experiment) and obtains an output (the outcome of the experiment). Experiments conducted by two or more parties in separate labs are hence described by their statistical correlations alone.

From Bell's theorem, we know that classical and quantum physics predict different sets of allowed correlations. It is expected, therefore, that far-from-quantum physical theories should predict correlations beyond the quantum set. In fact, there exist instances of theoretical non-quantum correlations which, a priori, do not seem physically implausible. The aim of device-independent reconstructions is to show that all such supra-quantum examples are precluded by a reasonable physical principle.

The physical principles proposed so far include no-signalling, Non-Trivial Communication Complexity, No-Advantage for Nonlocal computation, Information Causality, Macroscopic Locality, and Local Orthogonality. All these principles limit the set of possible correlations in non-trivial ways. Moreover, they are all device-independent: this means that they can be falsified under the assumption that we can decide if two or more events are space-like separated. The drawback of the device-independent approach is that, even when taken together, all the afore-mentioned physical principles do not suffice to single out the set of quantum correlations. In other words: all such reconstructions are partial.

Interpretations of quantum theory

Main article: Interpretations of quantum mechanics

An interpretation of quantum theory is a correspondence between the elements of its mathematical formalism and physical phenomena. For instance, in the pilot wave theory, the quantum wave function is interpreted as a field that guides the particle trajectory and evolves with it via a system of coupled differential equations. Most interpretations of quantum theory stem from the desire to solve the quantum measurement problem.

Extensions of quantum theory

In an attempt to reconcile quantum and classical physics, or to identify non-classical models with a dynamical causal structure, some modifications of quantum theory have been proposed.

Collapse models

Collapse models posit the existence of natural processes which periodically localize the wave-function. Such theories provide an explanation to the nonexistence of superpositions of macroscopic objects, at the cost of abandoning unitarity and exact energy conservation.

Quantum Measure Theory

In Sorkin's quantum measure theory (QMT), physical systems are not modeled via unitary rays and Hermitian operators, but through a single matrix-like object, the decoherence functional. The entries of the decoherence functional determine the feasibility to experimentally discriminate between two or more different sets of classical histories, as well as the probabilities of each experimental outcome. In some models of QMT the decoherence functional is further constrained to be positive semidefinite (strong positivity). Even under the assumption of strong positivity, there exist models of QMT which generate stronger-than-quantum Bell correlations.

Acausal quantum processes

The formalism of process matrices starts from the observation that, given the structure of quantum states, the set of feasible quantum operations follows from positivity considerations. Namely, for any linear map from states to probabilities one can find a physical system where this map corresponds to a physical measurement. Likewise, any linear transformation that maps composite states to states corresponds to a valid operation in some physical system. In view of this trend, it is reasonable to postulate that any high-order map from quantum instruments (namely, measurement processes) to probabilities should also be physically realizable. Any such map is termed a process matrix. As shown by Oreshkov et al., some process matrices describe situations where the notion of global causality breaks.

The starting point of this claim is the following mental experiment: two parties, Alice and Bob, enter a building and end up in separate rooms. The rooms have ingoing and outgoing channels from which a quantum system periodically enters and leaves the room. While those systems are in the lab, Alice and Bob are able to interact with them in any way; in particular, they can measure some of their properties.

Since Alice and Bob's interactions can be modeled by quantum instruments, the statistics they observe when they apply one instrument or another are given by a process matrix. As it turns out, there exist process matrices which would guarantee that the measurement statistics collected by Alice and Bob is incompatible with Alice interacting with her system at the same time, before or after Bob, or any convex combination of these three situations. Such processes are called acausal.

Altruism (biology)

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Altruism_(biology) 

In biology, altruism refers to behaviour by an individual that increases the fitness of another individual while decreasing the fitness of the agent. Altruism in this sense is different from the philosophical concept of altruism, in which an action would only be called "altruistic" if it was done with the conscious intention of helping another. In the behavioural sense, there is no such requirement. As such, it is not evaluated in moral terms—it is the consequences of an action for reproductive fitness that determine whether the action is considered altruistic, not the intentions, if any, with which the action is performed.

The term altruism was coined by the French philosopher Auguste Comte in French, as altruisme, for an antonym of egoism. He derived it from the Italian altrui, which in turn was derived from Latin alteri, meaning "other people" or "somebody else".

Altruistic behaviours appear most obviously in kin relationships, such as in parenting, but may also be evident among wider social groups, such as in social insects. They allow an individual to increase the success of its genes by helping relatives that share those genes. Obligate altruism is the permanent loss of direct fitness (with potential for indirect fitness gain). For example, honey bee workers may forage for the colony. Facultative altruism is temporary loss of direct fitness (with potential for indirect fitness gain followed by personal reproduction). For example, a Florida scrub jay may help at the nest, then gain parental territory.

Overview

In ethology (the study of behavior), and more generally in the study of social evolution, on occasion, some animals do behave in ways that reduce their individual fitness but increase the fitness of other individuals in the population; this is a functional definition of altruism. Research in evolutionary theory has been applied to social behaviour, including altruism. Cases of animals helping individuals to whom they are closely related can be explained by kin selection, and are not considered true altruism. Beyond the physical exertions that in some species mothers and in some species fathers undertake to protect their young, extreme examples of sacrifice may occur. One example is matriphagy (the consumption of the mother by her offspring) in the spider Stegodyphus; another example is a male spider allowing a female fertilized by him to eat him. Hamilton's rule describes the benefit of such altruism in terms of Wright's coefficient of relationship to the beneficiary and the benefit granted to the beneficiary minus the cost to the sacrificer. Should this sum be greater than zero a fitness gain will result from the sacrifice.

When apparent altruism is not between kin, it may be based on reciprocity. A monkey will present its back to another monkey, who will pick out parasites; after a time the roles will be reversed. Such reciprocity will pay off, in evolutionary terms, as long as the costs of helping are less than the benefits of being helped and as long as animals will not gain in the long run by "cheating"—that is to say, by receiving favours without returning them. This is elaborated on in evolutionary game theory and specifically the prisoner's dilemma as social theory.

Implications in evolutionary theory

Cooperative hunting by wolves allows them to tackle much larger and more nutritious prey than any individual wolf could handle. However, such cooperation could, potentially, be exploited by selfish individuals who do not expose themselves to the dangers of the hunt, but nevertheless share in the spoils.

The existence of altruism in nature is at first sight puzzling, because altruistic behaviour reduces the likelihood that an individual will reproduce. The idea that group selection might explain the evolution of altruism was first broached by Darwin himself in The Descent of Man, and Selection in Relation to Sex, (1871). The concept of group selection has had a chequered and controversial history in evolutionary biology but the uncritical 'good of the species' tradition came to an abrupt halt in the 1960s, due largely to the work of George C. Williams, and John Maynard Smith as well as Richard Dawkins. These evolutionary theorists pointed out that natural selection acts on the individual, and that it is the individual's fitness (number of offspring and grand-offspring produced compared to the rest of the population) that drives evolution. A group advantage (e.g. hunting in a pack) that is disadvantageous to the individual (who might be harmed during the hunt, when it could avoid injury by hanging back from the pack but still share in the spoils) cannot evolve, because the selfish individual will leave, on average, more offspring than those who join the pack and suffer injuries as a result. If the selfishness is hereditary, this will ultimately result in the population consisting entirely of selfish individuals. However, in the 1960s and 1970s an alternative to the "group selection" theory emerged. This was the kin selection theory, due originally to W. D. Hamilton. Kin selection is an instance of inclusive fitness, which is based on the notion that an individual shares only half its genes with each offspring, but also with each full sibling. From an evolutionary genetic point of view it is therefore as advantageous to help with the upbringing of full sibs as it is to produce and raise one's own offspring. The two activities are evolutionarily entirely equivalent. Co-operative breeding (i.e. helping one's parents raise sibs—provided they are full sibs) could thus evolve without the need for group-level selection. This quickly gained prominence among biologists interested in the evolution of social behaviour.

Olive baboons grooming

In 1971 Robert Trivers introduced his reciprocal altruism theory to explain the evolution of helping at the nest of an unrelated breeding pair of birds. He argued that an individual might act as a helper if there was a high probabilistic expectation of being helped by the recipients at some later date. If, however, the recipients did not reciprocate when it was possible to do so, the altruistic interaction with these recipients would be permanently terminated. But if the recipients did not cheat then the reciprocal altruism would continue indefinitely to both parties' advantage. This model was considered by many (e.g. West-Eberhard and Dawkins) to be evolutionarily unstable because it is prone to invasion by cheats for the same reason that cooperative hunting can be invaded and replaced by cheats. However, Trivers did make reference to the Prisoner's Dilemma Game which, 10 years later, would restore interest in Trivers' reciprocal altruism theory, but under the title of "tit-for-tat".

In its original form the Prisoner's Dilemma Game (PDG) described two awaiting trial prisoners, A and B, each faced with the choice of betraying the other or remaining silent. The "game" has four possible outcomes: (a) they both betray each other, and are both sentenced to two years in prison; (b) A betrays B, which sets A free and B is sentenced to four years in prison; (c) B betrays A, with the same result as (b) except that it is B who is set free and the other spends four years in jail; (d) both remain silent, resulting in a six-month sentence each. Clearly (d) ("cooperation") is the best mutual strategy, but from the point of view of the individual betrayal is unbeatable (resulting in being set free, or getting only a two-year sentence). Remaining silent results in a four-year or six-month sentence. This is exemplified by a further example of the PDG: two strangers attend a restaurant together and decide to split the bill. The mutually best ploy would be for both parties to order the cheapest items on the menu (mutual cooperation). But if one member of the party exploits the situation by ordering the most expensive items, then it is best for the other member to do likewise. In fact, if the fellow diner's personality is completely unknown, and the two diners are unlikely ever to meet again, it is always in one's own best interests to eat as expensively as possible. Situations in nature that are subject to the same dynamics (rewards and penalties) as the PDG define cooperative behaviour: it is never in the individual's fitness interests to cooperate, even though mutual cooperation rewards the two contestants (together) more highly than any other strategy. Cooperation cannot evolve under these circumstances.

However, in 1981 Axelrod and Hamilton noted that if the same contestants in the PDG meet repeatedly (the so-called Iterated Prisoner's Dilemma game, IPD) then tit-for-tat (foreshadowed by Robert Triver's reciprocal altruism theory) is a robust strategy which promotes altruism. In "tit-for-tat" both players' opening moves are cooperation. Thereafter each contestant repeats the other player's last move, resulting in a seemingly endless sequence of mutually cooperative moves. However, mistakes severely undermine tit-for-tat's effectiveness, giving rise to prolonged sequences of betrayal, which can only be rectified by another mistake. Since these initial discoveries, all the other possible IPD game strategies have been identified (16 possibilities in all, including, for instance, "generous tit-for-tat", which behaves like "tit-for-tat", except that it cooperates with a small probability when the opponent's last move was "betray"), but all can be outperformed by at least one of the other strategies, should one of the players switch to such a strategy. The result is that none is evolutionarily stable, and any prolonged series of the iterated prisoner's dilemma game, in which alternative strategies arise at random, gives rise to a chaotic sequence of strategy changes that never ends.

The handicap principle

 

A male peacock with its beautiful but clumsy, aerodynamically unsound tail—a handicap, comparable to a race horse's handicap.

 

The best horses in a handicap race carry the largest weights, so the size of the handicap is a measure of the animal's quality

In the light of the Iterated Prisoner's Dilemma Game failing to provide a full answer to the evolution of cooperation or altruism, several alternative explanations have been proposed.

There are striking parallels between altruistic acts and exaggerated sexual ornaments displayed by some animals, particularly certain bird species, such as, amongst others, the peacock. Both are costly in fitness terms, and both are generally conspicuous to other members of the population or species. This led Amotz Zahavi to suggest that both might be fitness signals rendered evolutionarily stable by his handicap principle. If a signal is to remain reliable, and generally resistant to falsification, the signal has to be evolutionarily costly. Thus, if a (low fitness) liar were to use the highly costly signal, which seriously eroded its real fitness, it would find it difficult to maintain a semblance or normality. Zahavi borrowed the term "handicap principle" from sports handicapping systems. These systems are aimed at reducing disparities in performance, thereby making the outcome of contests less predictable. In a horse handicap race, provenly faster horses are given heavier weights to carry under their saddles than inherently slower horses. Similarly, in amateur golf, better golfers have fewer strokes subtracted from their raw scores than the less talented players. The handicap therefore correlates with unhandicapped performance, making it possible, if one knows nothing about the horses, to predict which unhandicapped horse would win an open race. It would be the one handicapped with the greatest weight in the saddle. The handicaps in nature are highly visible, and therefore a peahen, for instance, would be able to deduce the health of a potential mate by comparing its handicap (the size of the peacock's tail) with those of the other males. The loss of the male's fitness caused by the handicap is offset by its increased access to females, which is as much of a fitness concern as is its health. An altruistic act is, by definition, similarly costly. It would therefore also signal fitness, and is probably as attractive to females as a physical handicap. If this is the case altruism is evolutionarily stabilized by sexual selection.

African pygmy kingfisher, showing details of appearance and colouration that are shared by all African pygmy kingfishers to a high degree of fidelity.

There is an alternate strategy for identifying fit mates which does not rely on one gender having exaggerated sexual ornaments or other handicaps, but is generally applicable to most, if not all sexual creatures. It derives from the concept that the change in appearance and functionality caused by a non-silent mutation will generally stand out in a population. This is because that altered appearance and functionality will be unusual, peculiar, and different from the norm within that population. The norm against which these unusual features are judged is made up of fit attributes that have attained their plurality through natural selection, while less adaptive attributes will be in the minority or frankly rare. Since the overwhelming majority of mutant features are maladaptive, and it is impossible to predict evolution's future direction, sexual creatures would be expected to prefer mates with the fewest unusual or minority features. This will have the effect of a sexual population rapidly shedding peripheral phenotypic features and canalizing the entire outward appearance and behaviour so that all the members of that population will begin to look remarkably similar in every detail, as illustrated in the accompanying photograph of the African pygmy kingfisher, Ispidina picta. Once a population has become as homogeneous in appearance as is typical of most species, its entire repertoire of behaviours will also be rendered evolutionarily stable, including any altruistic, cooperative and social characteristics. Thus, in the example of the selfish individual who hangs back from the rest of the hunting pack, but who nevertheless joins in the spoils, that individual will be recognized as being different from the norm, and will therefore find it difficult to attract a mate. Its genes will therefore have only a very small probability of being passed on to the next generation, thus evolutionarily stabilizing cooperation and social interactions at whatever level of complexity is the norm in that population.

Reciprocity mechanisms

Altruism in animals describes a range of behaviors performed by animals that may be to their own disadvantage but which benefit others. The costs and benefits are measured in terms of reproductive fitness, or expected number of offspring. So by behaving altruistically, an organism reduces the number of offspring it is likely to produce itself, but boosts the likelihood that other organisms are to produce offspring. There are other forms of altruism in nature other than risk-taking behavior, such as reciprocal altruism. This biological notion of altruism is not identical to the everyday human concept. For humans, an action would only be called 'altruistic' if it was done with the conscious intention of helping another. Yet in the biological sense there is no such requirement. Instead, until we can communicate directly with other species, an accurate theory to describe altruistic acts between species is Biological Market Theory. Humans and other animals exchange benefits in several ways, known technically as reciprocity mechanism. No matter what the mechanism, the common thread is that benefits find their way back to the original giver.

Symmetry-based

Also known as the "buddy-system", mutual affection between two parties prompts similar behavior in both directions without need to track of daily give-and-take, so long as the overall relationship remains satisfactory. This is one of the most common mechanism of reciprocity in nature, this kind is present in humans, primates, and many other mammals.

Attitudinal

Also known as, "If you're nice, I'll be nice too." This mechanism of reciprocity is similar to the heuristic of the golden rule, "Treat others how you would like to be treated." Parties mirror one another's attitudes, exchanging favors on the spot. Instant attitudinal reciprocity occurs among monkeys, and people often rely on it with strangers and acquaintances.

Calculated

Also known as, "what have you done for me lately?" Individuals keep track of the benefits they exchange with particular partners, which helps them decide to whom to return favors. This mechanism is typical of chimpanzees and very common among human relationships. Yet some opposing experimental research suggests that calculated or contingent reciprocity does not spontaneously arise in laboratory experimental settings, despite patterns of behavior.

Biological market theory

Biological market theory is an extension of the idea of reciprocal altruism, as a mechanism to explain altruistic acts between unrelated individuals in a more flexible system of exchanging commodities. The term 'biological market' was first used by Ronald Noe and Hammerstein in 1994 to refer to all the interactions between organisms in which different organisms function as 'traders' that exchange goods and services such as food and water, grooming, warning calls, shelter, etc. Biological market theory consists of five formal characteristics which present a basis for altruism.

1. Commodities are exchanged between individuals that differ in the degree of control over those commodities.
2. Trading partners are chosen from a number of potential partners.
3. There is competition among the members of the chosen class to be the most attractive partner. This competition by 'outbidding' causes an increase in the value of the commodity offered.
4. Supply and demand determine the bartering value of commodities exchanged.
5. Commodities on offer can be advertised. As in commercial advertisements there is a potential for false information.

Two bluestreak cleaner wrasses cleaning a potato cod

The applicability of biological market theory with its emphasis on partner choice is evident in the interactions between the cleaner wrasse and its "client" reef fish. Cleaners have small territories, which the majority of reef fish species actively visit to invite inspection of their surface, gills, and mouth. Clients benefit from the removal of parasites while cleaners benefit from the access to a food source. Some particularly choosy client species have large home ranges that cover several cleaning stations, whereas other clients have small ranges and have access to one cleaning station only (resident clients). Field observations, field manipulations, and laboratory experiments revealed that whether or not a client has choice options influences several aspects of both cleaner and client behaviour. Cleaners give choosy clients priority of access. Choosy clients switch partners if cheated by a cleaner by taking a bite of out of the cleaner, whereas resident clients punish cheats. Cleaners and resident clients, but not choosy clients, build up relationships before normal cleaning interactions take place. Cleaners are particularly cooperative if choosy clients are bystanders of an interaction but less so when resident clients are bystanders.

Researchers tested whether wild white-handed gibbon males from Khao Yai National Park, Thailand, increased their grooming activity when the female partner was fertile. Adult females and males of our study population are codominant (in terms of aggression), they live in pairs or small multi male groups and mate promiscuously. They found that males groomed females more than vice versa and more grooming was exchanged when females were cycling than during pregnancy or lactation. The number of copulations/day was elevated when females were cycling, and females copulated more frequently with males on days when they received more grooming. When males increased their grooming efforts, females also increased their grooming of males, perhaps to equalize give and take. Although grooming might be reciprocated because of intrinsic benefits of receiving grooming, males also interchange grooming as a commodity for sexual opportunities during a female's fertile period.

Examples in vertebrates

Mammals

• Wolves and wild dogs bring meat back to members of the pack not present at the kill. Though in harsh conditions, the breeding pair of wolves take the greatest share to continue to produce pups.
• Mongooses support elderly, sick, or injured animals.
• Meerkats often have one standing guard to warn while the rest feed in case of predator attack.
• Raccoons inform conspecifics about feeding grounds by droppings left on commonly shared latrines. A similar information system has been observed to be used by common ravens.
• Male baboons threaten predators and cover the rear as the troop retreats.
• Gibbons and chimpanzees with food will, in response to a gesture, share their food with others of the group. Chimpanzees will help humans and conspecifics without any reward in return.
• Bonobos have been observed aiding injured or disabled bonobos.
• Vampire bats commonly regurgitate blood to share with unlucky or sick roost mates that have been unable to find a meal, often forming a buddy system.
• Vervet monkeys give alarm calls to warn fellow monkeys of the presence of predators, even though in doing so they attract attention to themselves, increasing their personal chance of being attacked.
• Lemurs of all ages and of both sexes will take care of infants unrelated to them.
• Dolphins support sick or injured members of their pod, swimming under them for hours at a time and pushing them to the surface so they can breathe.
• Walruses have been seen adopting orphans who lost their parents to predators.
• African buffalo will rescue a member of the herd captured by predators. (See Battle at Kruger.)
• Humpback whales have been observed protecting other species from killer whales.
• Male Przewalski's horses have been observed engaging in intervention behaviour when their group members were threatened. They did not distinguish between kin and non-kin members. It has been theorized that they may do this to promote group cohesion and reduce social disruption within the group.

Birds

• In numerous bird species, a breeding pair receives support in raising its young from other "helper" birds, including help with the feeding of its fledglings. Some will even go as far as protecting an unrelated bird's young from predators.

Fish

• Harpagifer bispinis, a species of fish, live in social groups in the harsh environment of the Antarctic Peninsula. If the parent guarding the nest of eggs is removed, a usually male replacement unrelated to the parents guards the nest from predators and prevents fungal growth that would kill off the brood. There is no clear benefit to the male so the act may be considered altruistic.

Examples in invertebrates

• Some termites, such as Globitermes sulphureus and ants, such as Camponotus saundersi release a sticky secretion by fatally rupturing a specialized gland. This autothysis altruistically defends the colony at the expense of the individual insect. This can be attributed to the fact that ants share their genes with the entire colony, and so this behaviour is evolutionarily beneficial (not necessarily for the individual ant but for the continuation of its genetic make-up).
• Synalpheus regalis is a species of eusocial marine snapping shrimp that lives in sponges in coral reefs. They live in colonies of about 300 individuals with one reproductive female. Other colony members defend the colony against intruders, forage, and care for the young. Eusociality in this system entails an adaptive division of labor which results in enhanced reproductive output of the breeders and inclusive fitness benefits for the nonbreeding helpers. S. regalis are exceptionally tolerant of conspecifics within their colonies due to close genetic relatedness among nestmates. Allozyme data reveals that relatedness within colonies is high, which is an indication that colonies in this species represent close kin groups. The existence of such groups is an important prerequisite of explanations of social evolution based on kin selection.

Examples in protists

An example of altruism is found in the cellular slime moulds, such as Dictyostelium mucoroides. These protists live as individual amoebae until starved, at which point they aggregate and form a multicellular fruiting body in which some cells sacrifice themselves to promote the survival of other cells in the fruiting body.

Examples in plants

When it comes to altruism in kin/non-kin recognition, few studies have focused on this trait in crops. Despite most crops growing in monocultures, there is evidence that they are able to recognize kin and other cultivars. For example, cultivated soybean plants were able to recognize a distant ancestor and unrelated neighbors. In that experiment, plants were grown in combinations of relation to each other (same cultivar or different cultivar) in pots and their biomass of stems, leaves, and roots were measured to see how the plants responded growing next to kin or non-kin. Crops, unlike wild plants, are highly cultivated. The evolution of traits such as altruism can thus be bred into them through the selection of the trait. In agriculture, the importance of yield is stressed, therefore breeding crop cultivars to favor altruism can decrease competitiveness and increase yield. It has been shown that using mass selection early in the breeding process selects against altruism in an individual, but using mixed individual and group selection favors altruism.