Insects are the only group of invertebrates that have evolved wings and flight. Insects first flew in the Carboniferous, some 350 to 400 million years ago, making them the first animals to evolve flight. Wings may have evolved from appendages on the sides of existing limbs, which already had nerves, joints, and muscles used for other purposes. These may initially have been used for sailing on water, or to slow the rate of descent when gliding.
Two insect groups, the dragonflies and mayflies, have flight muscles attached directly to the wings. In other winged insects, flight muscles attach to the thorax, which make it oscillate in order to induce the wings to beat. Of these insects, some (flies and some beetles) achieve very high wingbeat frequencies through the evolution of an "asynchronous" nervous system, in which the thorax oscillates faster than the rate of nerve impulses.
Not all insects are capable of flight. A number of apterous insects have secondarily lost their wings through evolution, while other more basal insects like silverfish never evolved wings. In some eusocial insects like ants and termites, only the alate reproductive castes develop wings during the mating season before shedding their wings after mating, while the members of other castes are wingless their entire lives.
Some very small insects make use not of steady-state aerodynamics, but of the Weis-Fogh clap and fling mechanism, generating large lift forces at the expense of wear and tear on the wings. Many insects can hover, maintaining height and controlling their position. Some insects such as moths have the forewings coupled to the hindwings so these can work in unison.
Mechanisms
Direct flight
Unlike other insects, the wing muscles of the Ephemeroptera (mayflies) and Odonata (dragonflies and damselflies) insert directly at the wing bases, which are hinged so that a small downward movement of the wing base lifts the wing itself upward, much like rowing through the air. Dragonflies and damselflies have fore and hind wings similar in shape and size. Each operates independently, which gives a degree of fine control and mobility in terms of the abruptness with which they can change direction and speed, not seen in other flying insects. Odonates are all aerial predators, and they have always hunted other airborne insects.
Indirect flight
Other than the two orders with direct flight muscles, all other living winged insects fly using a different mechanism, involving indirect flight muscles. This mechanism evolved once and is the defining feature (synapomorphy) for the infraclass Neoptera; it corresponds, probably not coincidentally, with the appearance of a wing-folding mechanism, which allows Neopteran insects to fold the wings back over the abdomen when at rest (though this ability has been lost secondarily in some groups, such as in the butterflies).
What all Neoptera share, however, is the way the muscles in the thorax work: these muscles, rather than attaching to the wings, attach to the thorax and deform it; since the wings are extensions of the thoracic exoskeleton, the deformations of the thorax cause the wings to move as well. A set of longitudinal muscles along the back compresses the thorax from front to back, causing the dorsal surface of the thorax (notum) to bow upward, making the wings flip down. Another set of muscles from the tergum to the sternum pulls the notum downward again, causing the wings to flip upward.
The Neoptera, including butterflies and most other insects, have indirect flight musculature
Insects that beat their wings fewer than one hundred times a second use synchronous muscle. Synchronous muscle is a type of muscle that contracts once for every nerve impulse. This generally produces less power and is less efficient than asynchronous muscle, which accounts for the independent evolution of asynchronous flight muscles in several separate insect clades.
Insects that beat their wings more rapidly, such as the bumblebee, use asynchronous muscle; this is a type of muscle that contracts more than once per nerve impulse. This is achieved by the muscle being stimulated to contract again by a release in tension in the muscle, which can happen more rapidly than through simple nerve stimulation alone. This allows the frequency of wing beats to exceed the rate at which the nervous system can send impulses. The asynchronous muscle is one of the final refinements that has appeared in some of the higher Neoptera (Coleoptera, Diptera, and Hymenoptera). The overall effect is that many higher Neoptera can beat their wings much faster than insects with direct flight muscles.
Aerodynamics
There are two basic aerodynamic models of insect flight: creating a leading edge vortex, and using clap and fling.
Leading edge vortex
Most insects use a method that creates a spiralling leading edge vortex. These flapping wings move through two basic half-strokes. The downstroke starts up and back and is plunged downward and forward. Then the wing is quickly flipped over (supination) so that the leading edge is pointed backward. The upstroke then pushes the wing upward and backward. Then the wing is flipped again (pronation) and another downstroke can occur. The frequency range in insects with synchronous flight muscles typically is 5 to 200 hertz (Hz). In those with asynchronous flight muscles, wing beat frequency may exceed 1000 Hz. When the insect is hovering, the two strokes take the same amount of time. A slower downstroke, however, provides thrust.
Identification of major forces is critical to understanding insect flight. The first attempts to understand flapping wings assumed a quasi-steady state. This means that the air flow over the wing at any given time was assumed to be the same as how the flow would be over a non-flapping, steady-state wing at the same angle of attack. By dividing the flapping wing into a large number of motionless positions and then analyzing each position, it would be possible to create a timeline of the instantaneous forces on the wing at every moment. The calculated lift was found to be too small by a factor of three, so researchers realized that there must be unsteady phenomena providing aerodynamic forces. There were several developing analytical models attempting to approximate flow close to a flapping wing. Some researchers predicted force peaks at supination. With a dynamically scaled model of a fruit fly, these predicted forces later were confirmed. Others argued that the force peaks during supination and pronation are caused by an unknown rotational effect that fundamentally is different from the translational phenomena. There is some disagreement with this argument. Through computational fluid dynamics, some researchers argue that there is no rotational effect. They claim that the high forces are caused by an interaction with the wake shed by the previous stroke.
Similar to the rotational effect mentioned above, the phenomena associated with flapping wings are not completely understood or agreed upon. Because every model is an approximation, different models leave out effects that are presumed to be negligible. For example, the Wagner effect, as proposed by Herbert A. Wagner in 1925, says that circulation rises slowly to its steady-state due to viscosity when an inclined wing is accelerated from rest. This phenomenon would explain a lift value that is less than what is predicted. Typically, the case has been to find sources for the added lift. It has been argued that this effect is negligible for flow with a Reynolds number that is typical of insect flight. The Reynolds number is a measure of turbulence; flow is laminar (smooth) when the Reynolds number is low, and turbulent when it is high. The Wagner effect was ignored, consciously, in at least one model. One of the most important phenomena that occurs during insect flight is leading edge suction. This force is significant to the calculation of efficiency. The concept of leading edge suction first was put forth by D. G. Ellis and J. L. Stollery in 1988 to describe vortex lift on sharp-edged delta wings. At high angles of attack, the flow separates over the leading edge, but reattaches before reaching the trailing edge. Within this bubble of separated flow is a vortex. Because the angle of attack is so high, a lot of momentum is transferred downward into the flow. These two features create a large amount of lift force as well as some additional drag. The important feature, however, is the lift. Because the flow has separated, yet it still provides large amounts of lift, this phenomenon is called stall delay, first noticed on aircraft propellers by H. Himmelskamp in 1945. This effect was observed in flapping insect flight and it was proven to be capable of providing enough lift to account for the deficiency in the quasi-steady-state models. This effect is used by canoeists in a sculling draw stroke.
All of the effects on a flapping wing may be reduced to three major sources of aerodynamic phenomena: the leading edge vortex, the steady-state aerodynamic forces on the wing, and the wing’s contact with its wake from previous strokes. The size of flying insects ranges from about 20 micrograms to about 3 grams. As insect body mass increases, wing area increases and wing beat frequency decreases. For larger insects, the Reynolds number (Re) may be as high as 10000, where flow is starting to become turbulent. For smaller insects, it may be as low as 10. This means that viscous effects are much more important to the smaller insects.
Another interesting feature of insect flight is the body tilt. As flight speed increases, the insect body tends to tilt nose-down and become more horizontal. This reduces the frontal area and therefore, the body drag. Since drag also increases as forward velocity increases, the insect is making its flight more efficient as this efficiency becomes more necessary. Additionally, by changing the geometric angle of attack on the downstroke, the insect is able to keep its flight at an optimal efficiency through as many manoeuvres as possible. The development of general thrust is relatively small compared with lift forces. Lift forces may be more than three times the insect's weight, while thrust at even the highest speeds may be as low as 20% of the weight. This force is developed primarily through the less powerful upstroke of the flapping motion.
Clap and fling
Clap and fling, or the Weis-Fogh mechanism, discovered by the Danish zoologist Torkel Weis-Fogh, is a lift generation method utilized during small insect flight. As insect sizes become less than 1 mm, viscous forces become dominant and the efficacy of lift generation from an airfoil decreases drastically. Starting from the clap position, the two wings fling apart and rotate about the trailing edge. The wings then separate and sweep horizontally until the end of the downstroke. Next, the wings pronate and utilize the leading edge during an upstroke rowing motion. As the clap motion begins, the leading edges meet and rotate together until the gap vanishes. Initially, it was thought that the wings were touching, but several incidents indicate a gap between the wings and suggest it provides an aerodynamic benefit.
Lift generation from the clap and fling mechanism occurs during several processes throughout the motion. First, the mechanism relies on a wing-wing interaction, as a single wing motion does not produce sufficient lift. As the wings rotate about the trailing edge in the flinging motion, air rushes into the created gap and generates a strong leading edge vortex, and a second one developing at the wingtips. A third, weaker, vortex develops on the trailing edge. The strength of the developing vortices relies, in-part, on the initial gap of the inter-wing separation at the start of the flinging motion. With a decreased gap inter-wing gap indicating a larger lift generation, at the cost of larger drag forces. The implementation of a heaving motion during fling, flexible wings, and a delayed stall mechanism were found to reinforce vortex stability and attachment. Finally, to compensate the overall lower lift production during low Reynolds number flight (with laminar flow), tiny insects often have a higher stroke frequency to generate wing-tip velocities that are comparable to larger insects.
The overall largest expected drag forces occur during the dorsal fling motion, as the wings need to separate and rotate. The attenuation of the large drag forces occur through several mechanisms. Flexible wings were found to decrease the drag in flinging motion by up to 50% and further reduce the overall drag through the entire wing stroke when compared to rigid wings. Bristles on the wing edges, as seen in Encarsia formosa, cause a porosity in the flow which augments and reduces the drag forces, at the cost of lower lift generation. Further, the inter-wing separation before fling plays an important role in the overall effect of drag. As the distance increases between the wings, the overall drag decreases.
The clap and fling mechanism is also employed by the marine mollusc Limacina helicina, a sea butterfly. Some insects, such as the vegetable leaf miner Liriomyza sativae (a fly), exploit a partial clap and fling, using the mechanism only on the outer part of the wing to increase lift by some 7% when hovering.
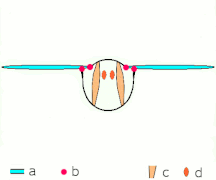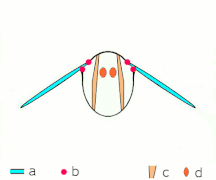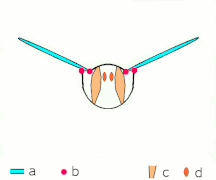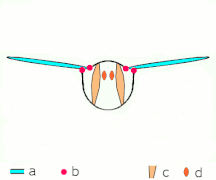
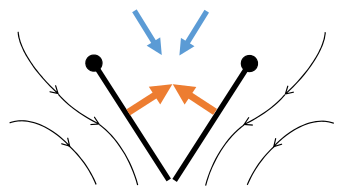
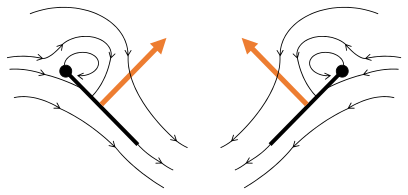
- Clap and fling flight mechanism after Sane 2003
Clap 2: leading edges touch, wing rotates around leading edge, vortices form
- Black (curved) arrows: flow; Blue arrows: induced velocity; Orange arrows: net force on wing
Fling 3: new vortex forms at leading edge, trailing edge vortices cancel each other, perhaps helping flow to grow faster (Weis-Fogh 1973)
Governing equations
A wing moving in fluids experiences a fluid force, which follows the conventions found in aerodynamics. The force component normal to the direction of the flow relative to the wing is called lift (L), and the force component in the opposite direction of the flow is drag (D). At the Reynolds numbers considered here, an appropriate force unit is 1/2(ρU2S), where ρ is the density of the fluid, S the wing area, and U the wing speed. The dimensionless forces are called lift (CL) and drag (CD) coefficients, that is:
CL and CD are constants only if the flow is steady. A special class of objects such as airfoils may reach a steady state when it slices through the fluid at a small angle of attack. In this case, the inviscid flow around an airfoil can be approximated by a potential flow satisfying the no-penetration boundary condition. The Kutta-Joukowski theorem of a 2D airfoil further assumes that the flow leaves the sharp trailing edge smoothly, and this determines the total circulation around an airfoil. The corresponding lift is given by Bernoulli's principle (Blasius theorem):
The flows around birds and insects can be considered incompressible: The Mach number, or velocity relative to the speed of sound in air, is typically 1/300 and the wing frequency is about 10–103 Hz. Using the governing equation as the Navier-Stokes equation being subject to the no-slip boundary condition, the equation is:
Where u(x, t) is the flow field, p the pressure, ρ the density of the fluid, ν the kinematic viscosity, ubd the velocity at the boundary, and us the velocity of the solid. By choosing a length scale, L, and velocity scale, U, the equation can be expressed in nondimensional form containing the Reynolds number, Re=uL/ν . There are two obvious differences between an insect wing and an airfoil: An insect wing is much smaller and it flaps. Using a dragonfly as an example, Its chord (c) is about 1 cm (0.39 in), its wing length (l) about 4 cm (1.6 in), and its wing frequency (f) about 40 Hz. The tip speed (u) is about 1 m/s (3.3 ft/s), and the corresponding Reynolds number about 103. At the smaller end, a typical chalcidoid wasp has a wing length of about 0.5–0.7 mm (0.020–0.028 in) and beats its wing at about 400 Hz. Its Reynolds number is about 25. The range of Reynolds number in insect flight is about 10 to 104, which lies in between the two limits that are convenient for theories: inviscid steady flows around an airfoil and Stokes flow experienced by a swimming bacterium. For this reason, this intermediate range is not well understood. On the other hand, it is perhaps the most ubiquitous regime among the things we see. Falling leaves and seeds, fishes, and birds all encounter unsteady flows similar to that seen around an insect. The chordwise Reynolds number can be described by:
and
Where is the average chord length, is the speed of the wing tip, is the stroke amplitude, is the beat frequency, is the radius of gyration, is the wing area, and is the length of wing, including the wing tip.
In addition to the Reynolds number, there are at least two other relevant dimensionless parameters. A wing has three velocity scales: the flapping velocity with respect to the body (u), the forward velocity of the body (U0), and the pitching velocity (Ωc). The ratios of them form two dimensionless variables, U0/u and Ωc/u, the former is often referred to as the advance ratio, and it is also related to the reduced frequency, fc/U0.
If an insect wing is rigid, for example, a Drosophila wing is approximately so, its motion relative to a fixed body can be described by three variables: the position of the tip in spherical coordinates, (Θ(t),Φ(t)), and the pitching angle ψ(t), about the axis connecting the root and the tip. To estimate the aerodynamic forces based on blade-element analysis, it is also necessary to determine the angle of attack (α). The typical angle of attack at 70% wingspan ranges from 25° to 45° in hovering insects (15° in hummingbirds). Despite the wealth of data available for many insects, relatively few experiments report the time variation of α during a stroke. Among these are wind tunnel experiments of a tethered locust and a tethered fly, and free hovering flight of a fruit fly.
Because they are relatively easy to measure, the wing-tip trajectories have been reported more frequently. For example, selecting only flight sequences that produced enough lift to support a weight, will show that the wing tip follows an elliptical shape. Noncrossing shapes were also reported for other insects. Regardless of their exact shapes, the plugging-down motion indicates that insects may use aerodynamic drag in addition to lift to support its weight.
Hovering
| Flight parameters | Speed (m/s) | Beats/s |
|---|---|---|
| Aeshnid dragonfly | 7.0 | 38 |
| Hornet | 5.7 | 100 |
| Hummingbird hawkmoth | 5.0 | 85 |
| Horsefly | 3.9 | 96 |
| Hoverfly | 3.5 | 120 |
| Bumblebee | 2.9 | 130 |
| Honeybee | 2.5 | 250 |
| Housefly | 2.0 | 190 |
| Damselfly | 1.5 | 16 |
| Scorpionfly | 0.49 | 28 |
| Large white butterfly | 2.5 | 12 |
| Thrips (clap and fling) | 0.3 | 254 |
Many insects can hover, or stay in one spot in the air, doing so by beating their wings rapidly. Doing so requires sideways stabilization as well as the production of lift. The lifting force is mainly produced by the downstroke. As the wings push down on the surrounding air, the resulting reaction force of the air on the wings pushes the insect up. The wings of most insects are evolved so that, during the upward stroke, the force on the wing is small. Since the downbeat and return stroke force the insect up and down respectively, the insect oscillates and winds up staying in the same position.
The distance the insect falls between wingbeats depends on how rapidly its wings are beating: the slower it flaps, the longer the interval in which it falls, and the farther it falls between each wingbeat. One can calculate the wingbeat frequency necessary for the insect to maintain a given stability in its amplitude. To simplify the calculations, one must assume that the lifting force is at a finite constant value while the wings are moving down and that it is zero while the wings are moving up. During the time interval Δt of the upward wingbeat, the insect drops a distance h under the influence of gravity.
The upward stroke then restores the insect to its original position. Typically, it may be required that the vertical position of the insect changes by no more than 0.1 mm (i.e., h = 0.1 mm). The maximum allowable time for free fall is then
Since the up movements and the down movements of the wings are about equal in duration, the period T for a complete up-and-down wing is twice Δr, that is,
The frequency of the beats, f, meaning the number of wingbeats per second, is represented by the equation:
In the examples used the frequency used is 110 beats/s, which is the typical frequency found in insects. Butterflies have a much slower frequency with about 10 beats/s, which means that they can't hover. Other insects may be able to produce a frequency of 1000 beats/s. To restore the insect to its original vertical position, the average upward force during the downward stroke, Fav, must be equal to twice the weight of the insect. Note that since the upward force on the insect body is applied only for half the time, the average upward force on the insect is simply its weight.
Power input
One can now compute the power required to maintain hovering by, considering again an insect with mass m 0.1 g, average force, Fav, applied by the two wings during the downward stroke is two times the weight. Because the pressure applied by the wings is uniformly distributed over the total wing area, that means one can assume the force generated by each wing acts through a single point at the midsection of the wings. During the downward stroke, the center of the wings traverses a vertical distance d. The total work done by the insect during each downward stroke is the product of force and distance; that is,
If the wings swing through the beat at an angle of 70°, then in the case presented for the insect with 1 cm long wings, d is 0.57 cm. Therefore, the work done during each stroke by the two wings is:
The energy is used to raise the insect against gravity. The energy E required to raise the mass of the insect 0.1 mm during each downstroke is:
This is a negligible fraction of the total energy expended which clearly, most of the energy is expended in other processes. A more detailed analysis of the problem shows that the work done by the wings is converted primarily into kinetic energy of the air that is accelerated by the downward stroke of the wings. The power is the amount of work done in 1 s; in the insect used as an example, makes 110 downward strokes per second. Therefore, its power output P is, strokes per second, and that means its power output P is:
Power output
In the calculation of the power used in hovering, the examples used neglected the kinetic energy of the moving wings. The wings of insects, light as they are, have a finite mass; therefore, as they move they possess kinetic energy. Because the wings are in rotary motion, the maximum kinetic energy during each wing stroke is:
Here I is the moment of inertia of the wing and ωmax is the maximum angular velocity during the wing stroke. To obtain the moment of inertia for the wing, we will assume that the wing can be approximated by a thin rod pivoted at one end. The moment of inertia for the wing is then:
Where l is the length of the wing (1 cm) and m is the mass of two wings, which may be typically 10−3 g. The maximum angular velocity, ωmax, can be calculated from the maximum linear velocity, νmax, at the center of the wing:
During each stroke the center of the wings moves with an average linear velocity νav given by the distance d traversed by the center of the wing divided by the duration Δt of the wing stroke. From our previous example, d = 0.57 cm and Δt = 4.5×10−3 s. Therefore:
The velocity of the wings is zero both at the beginning and at the end of the wing stroke, meaning the maximum linear velocity is higher than the average velocity. If we assume that the velocity oscillates (sinusoidally) along the wing path, the maximum velocity is twice as high as the average velocity. Therefore, the maximum angular velocity is:
And the kinetic energy therefore is:
Since there are two wing strokes (the upstroke and downstroke) in each cycle of the wing movement, the kinetic energy is 2×43 = 86 erg. This is about as much energy as is consumed in hovering itself.
Elasticity
Insects gain kinetic energy, provided by the muscles, when the wings accelerate. When the wings begin to decelerate toward the end of the stroke, this energy must dissipate. During the downstroke, the kinetic energy is dissipated by the muscles themselves and is converted into heat (this heat is sometimes used to maintain core body temperature). Some insects are able to utilize the kinetic energy in the upward movement of the wings to aid in their flight. The wing joints of these insects contain a pad of elastic, rubber-like protein called resilin. During the upstroke of the wing, the resilin is stretched. The kinetic energy of the wing is converted into potential energy in the stretched resilin, which stores the energy much like a spring. When the wing moves down, this energy is released and aids in the downstroke.
Using a few simplifying assumptions, we can calculate the amount of energy stored in the stretched resilin. Although the resilin is bent into a complex shape, the example given shows the calculation as a straight rod of area A and length. Furthermore, we will assume that throughout the stretch the resilin obeys Hooke's law. This is not strictly true as the resilin is stretched by a considerable amount and therefore both the area and Young's modulus change in the process of stretching. The potential energy U stored in the stretched resilin is:
Here E is the Young’s modulus for resilin, which has been measured to be 1.8×107 dyn/cm2. Typically in an insect the size of a bee, the volume of the resilin may be equivalent to a cylinder 2×10−2 cm long and 4×10−4 cm2 in area. In the example given, the length of the resilin rod is increased by 50% when stretched. That is, Δℓ is 10−2 cm. Therefore, in this case the potential energy stored in the resilin of each wing is:
The stored energy in the two wings for a bee-sized insect is 36 erg, which is comparable to the kinetic energy in the upstroke of the wings. Experiments show that as much as 80% of the kinetic energy of the wing may be stored in the resilin.
Wing coupling
Some four-winged insect orders, such as the Lepidoptera, have developed morphological wing coupling mechanisms in the imago which render these taxa functionally two-winged. All but the most basal forms exhibit this wing-coupling.
The mechanisms are of three different types - jugal, frenulo-retinacular and amplexiform:
- The more primitive groups have an enlarged lobe-like area near the basal posterior margin, i.e. at the base of the forewing, a jugum, that folds under the hindwing in flight.
- Other groups have a frenulum on the hindwing that hooks under a retinaculum on the forewing.
- In almost all butterflies and in the Bombycoidea (except the Sphingidae), there is no arrangement of frenulum and retinaculum to couple the wings. Instead, an enlarged humeral area of the hindwing is broadly overlapped by the forewing. Despite the absence of a specific mechanical connection, the wings overlap and operate in phase. The power stroke of the forewing pushes down the hindwing in unison. This type of coupling is a variation of frenate type but where the frenulum and retinaculum are completely lost.
Biochemistry
The biochemistry of insect flight has been a focus of considerable study. While many insects use carbohydrates and lipids as the energy source for flight, many beetles and flies use the amino acid proline as their energy source. Some species also use a combination of sources and moths such as Manduca sexta use carbohydrates for pre-flight warm-up.
Sensory Feedback
Insects use sensory feedback to maintain and control flight. Research has demonstrated the role of sensory structures such as antennae, halteres and wings in controlling flight posture, wingbeat amplitude, and wingbeat frequency.
Evolution and adaptation
Sometime in the Carboniferous Period, some 350 to 400 million years ago, when there were only two major land masses, insects began flying. Among the oldest winged insect fossils is Delitzschala, a Palaeodictyopteran from the Lower Carboniferous; Rhyniognatha is older, from the Early Devonian, but it is uncertain if it had wings, or indeed was an insect.
How and why insect wings developed is not well understood, largely due to the scarcity of appropriate fossils from the period of their development in the Lower Carboniferous. There have historically been three main theories on the origins of insect flight. The first was that they are modifications of movable abdominal gills, as found on aquatic naiads of mayflies. Phylogenomic analysis suggests that the Polyneoptera, the group of winged insects that includes grasshoppers, evolved from a terrestrial ancestor, making the evolution of wings from gills unlikely. Additional study of the jumping behavior of mayfly larvae has determined that tracheal gills play no role in guiding insect descent, providing further evidence against this evolutionary hypothesis. This leaves two major historic theories: that wings developed from paranotal lobes, extensions of the thoracic terga; or that they arose from modifications of leg segments, which already contained muscles.
Epicoxal (abdominal gill) hypothesis
Numerous entomologists including Landois in 1871, Lubbock in 1873, Graber in 1877, and Osborn in 1905 have suggested that a possible origin for insect wings might have been movable abdominal gills found in many aquatic insects, such as on naiads of mayflies. According to this theory these tracheal gills, which started their way as exits of the respiratory system and over time were modified into locomotive purposes, eventually developed into wings. The tracheal gills are equipped with little winglets that perpetually vibrate and have their own tiny straight muscles.
Paranotal (tergal) hypothesis
The paranotal lobe or tergal (dorsal body wall) hypothesis, proposed by Fritz Müller in 1875 and reworked by G. Crampton in 1916, Jarmila Kulakova-Peck in 1978 and Alexander P. Rasnitsyn in 1981 among others, suggests that the insect's wings developed from paranotal lobes, a preadaptation found in insect fossils that would have assisted stabilization while hopping or falling. In favor of this hypothesis is the tendency of most insects, when startled while climbing on branches, to escape by dropping to the ground. Such lobes would have served as parachutes and enable the insect to land more softly. The theory suggests that these lobes gradually grew larger and in a later stage developed a joint with the thorax. Even later would appear the muscles to move these crude wings. This model implies a progressive increase in the effectiveness of the wings, starting with parachuting, then gliding and finally active flight. Still, lack of substantial fossil evidence of the development of the wing joints and muscles poses a major difficulty to the theory, as does the seemingly spontaneous development of articulation and venation, and it has been largely rejected by experts in the field.
Endite-exite (pleural) hypothesis
In 1990, J. W. H. Trueman proposed that the wing was adapted from endites and exites, appendages on the respective inner and outer aspects of the primitive arthropod limb, also called the pleural hypothesis. This was based on a study by Goldschmidt in 1945 on Drosophila melanogaster, in which a variation called "pod" (for podomeres, limb segments) displayed a mutation that transformed normal wings. The result was interpreted as a triple-jointed leg arrangement with some additional appendages but lacking the tarsus, where the wing's costal surface would normally be. This mutation was reinterpreted as strong evidence for a dorsal exite and endite fusion, rather than a leg, with the appendages fitting in much better with this hypothesis. The innervation, articulation and musculature required for the evolution of wings are already present in the limb segments.
Other hypotheses
Other hypotheses include Vincent Wigglesworth's 1973 suggestion that wings developed from thoracic protrusions used as radiators.
Adrian Thomas and Åke Norberg suggested in 2003 that wings may have evolved initially for sailing on the surface of water as seen in some stoneflies.
Stephen P. Yanoviak and colleagues proposed in 2009 that the wing derives from directed aerial gliding descent—a preflight phenomenon found in some apterygota, a wingless sister taxon to the winged insects.
Dual origin
Biologists including Averof, Niwa, Elias-Neto and their colleagues have begun to explore the origin of the insect wing using evo-devo in addition to palaeontological evidence. This suggests that wings are serially homologous with both tergal and pleural structures, potentially resolving the centuries-old debate. Jakub Prokop and colleagues have in 2017 found palaeontological evidence from Paleozoic nymphal wing pads that wings indeed had such a dual origin.