From Wikipedia, the free encyclopedia
In artificial intelligence (AI), commonsense reasoning is a human-like ability to make presumptions about the type and essence of ordinary situations humans encounter every day. These assumptions include judgments about the nature of physical objects, taxonomic properties, and peoples' intentions. A device that exhibits commonsense reasoning might be capable of drawing conclusions that are similar to humans' folk psychology (humans' innate ability to reason about people's behavior and intentions) and naive physics (humans' natural understanding of the physical world).
Definitions and characterizations
Some definitions and characterizations of common sense from different authors include:
- "Commonsense knowledge includes the basic facts about events (including actions) and their effects, facts about knowledge and how it is obtained, facts about beliefs and desires. It also includes the basic facts about material objects and their properties."
- "Commonsense knowledge differs from encyclopedic knowledge in that it deals with general knowledge rather than the details of specific entities."
- Commonsense knowledge is "real world knowledge that can provide a basis for additional knowledge to be gathered and interpreted automatically".
- The commonsense world consists of "time, space, physical interactions, people, and so on".
- Common sense is "all the knowledge about the world that we take for granted but rarely state out loud".
- Common sense is "broadly reusable background knowledge that's not specific to a particular subject area... knowledge that you ought to have."
NYU professor Ernest Davis characterizes commonsense knowledge as "what a typical seven year old knows about the world", including physical objects, substances, plants, animals, and human society. It usually excludes book-learning, specialized knowledge, and knowledge of conventions; but it sometimes includes knowledge about those topics. For example, knowing how to play cards is specialized knowledge, not "commonsense knowledge"; but knowing that people play cards for fun does count as "commonsense knowledge".
Commonsense reasoning problem

Compared with humans, existing AI lacks several features of human commonsense reasoning; most notably, humans have powerful mechanisms for reasoning about "naïve physics" such as space, time, and physical interactions. This enables even young children to easily make inferences like "If I roll this pen off a table, it will fall on the floor". Humans also have a powerful mechanism of "folk psychology" that helps them to interpret natural-language sentences such as "The city councilmen refused the demonstrators a permit because they advocated violence". (A generic AI has difficulty discerning whether the ones alleged to be advocating violence are the councilmen or the demonstrators.) This lack of "common knowledge" means that AI often makes different mistakes than humans make, in ways that can seem incomprehensible. For example, existing self-driving cars cannot reason about the location nor the intentions of pedestrians in the exact way that humans do, and instead must use non-human modes of reasoning to avoid accidents.
Overlapping subtopics of commonsense reasoning include quantities and measurements, time and space, physics, minds, society, plans and goals, and actions and change.
Commonsense knowledge problem
The commonsense knowledge problem is a current project in the sphere of artificial intelligence to create a database that contains the general knowledge most individuals are expected to have, represented in an accessible way to artificial intelligence programs that use natural language. Due to the broad scope of the commonsense knowledge, this issue is considered to be among the most difficult problems in AI research. In order for any task to be done as a human mind would manage it, the machine is required to appear as intelligent as a human being. Such tasks include object recognition, machine translation and text mining. To perform them, the machine has to be aware of the same concepts that an individual, who possess commonsense knowledge, recognizes.
Commonsense in intelligent tasks
In 1961, Bar Hillel first discussed the need and significance of practical knowledge for natural language processing in the context of machine translation. Some ambiguities are resolved by using simple and easy to acquire rules. Others require a broad acknowledgement of the surrounding world, thus they require more commonsense knowledge. For instance, when a machine is used to translate a text, problems of ambiguity arise, which could be easily resolved by attaining a concrete and true understanding of the context. Online translators often resolve ambiguities using analogous or similar words. For example, in translating the sentences "The electrician is working" and "The telephone is working" into German, the machine translates correctly "working" in the means of "laboring" in the first one and as "functioning properly" in the second one. The machine has seen and read in the body of texts that the German words for "laboring" and "electrician" are frequently used in a combination and are found close together. The same applies for "telephone" and "function properly". However, the statistical proxy which works in simple cases often fails in complex ones. Existing computer programs carry out simple language tasks by manipulating short phrases or separate words, but they don't attempt any deeper understanding and focus on short-term results.
Computer vision
Issues of this kind arise in computer vision. For instance when looking at a photograph of a bathroom some items that are small and only partly seen, such as facecloths and bottles, are recognizable due to the surrounding objects (toilet, wash basin, bathtub), which suggest the purpose of the room. In an isolated image they would be difficult to identify. Movies prove to be even more difficult tasks. Some movies contain scenes and moments that cannot be understood by simply matching memorized templates to images. For instance, to understand the context of the movie, the viewer is required to make inferences about characters’ intentions and make presumptions depending on their behavior. In the contemporary state of the art, it is impossible to build and manage a program that will perform such tasks as reasoning, i.e. predicting characters’ actions. The most that can be done is to identify basic actions and track characters.
Robotic manipulation
The need and importance of commonsense reasoning in autonomous robots that work in a real-life uncontrolled environment is evident. For instance, if a robot is programmed to perform the tasks of a waiter at a cocktail party, and it sees that the glass he had picked up is broken, the waiter-robot should not pour the liquid into the glass, but instead pick up another one. Such tasks seem obvious when an individual possesses simple commonsense reasoning, but to ensure that a robot will avoid such mistakes is challenging.
Successes in automated commonsense reasoning
Significant progress in the field of the automated commonsense reasoning is made in the areas of the taxonomic reasoning, actions and change reasoning, reasoning about time. Each of these spheres has a well-acknowledged theory for wide range of commonsense inferences.
Taxonomic reasoning
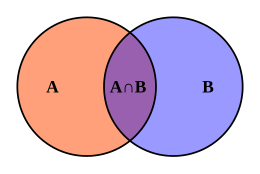
Taxonomy is the collection of individuals and categories and their relations. Three basic relations are:
- An individual is an instance of a category. For example, the individual Tweety is an instance of the category robin.
- One category is a subset of another. For instance robin is a subset of bird.
- Two categories are disjoint. For instance robin is disjoint from penguin.
Transitivity is one type of inference in taxonomy. Since Tweety is an instance of robin and robin is a subset of bird, it follows that Tweety is an instance of bird. Inheritance is another type of inference. Since Tweety is an instance of robin, which is a subset of bird and bird is marked with property canfly, it follows that Tweety and robin have property canfly. When an individual taxonomizes more abstract categories, outlining and delimiting specific categories becomes more problematic. Simple taxonomic structures are frequently used in AI programs. For instance, WordNet is a resource including a taxonomy, whose elements are meanings of English words. Web mining systems used to collect commonsense knowledge from Web documents focus on taxonomic relations and specifically in gathering taxonomic relations.
Action and change
The theory of action, events and change is another range of the commonsense reasoning. There are established reasoning methods for domains that satisfy the constraints listed below:
- Events are atomic, meaning one event occurs at a time and the reasoner needs to consider the state and condition of the world at the start and at the finale of the specific event, but not during the states, while there is still an evidence of on-going changes (progress).
- Every single change is a result of some event
- Events are deterministic, meaning the world's state at the end of the event is defined by the world's state at the beginning and the specification of the event.
- There is a single actor and all events are their actions.
- The relevant state of the world at the beginning is either known or can be calculated.
Temporal reasoning
Temporal reasoning is the ability to make presumptions about humans' knowledge of times, durations and time intervals. For example, if an individual knows that Mozart was born after Haydn and died earlier than him, they can use their temporal reasoning knowledge to deduce that Mozart had died younger than Haydn. The inferences involved reduce themselves to solving systems of linear inequalities. To integrate that kind of reasoning with concrete purposes, such as natural language interpretation, is more challenging, because natural language expressions have context dependent interpretation. Simple tasks such as assigning timestamps to procedures cannot be done with total accuracy.
Qualitative reasoning
Qualitative reasoning is the form of commonsense reasoning analyzed with certain success. It is concerned with the direction of change in interrelated quantities. For instance, if the price of a stock goes up, the amount of stocks that are going to be sold will go down. If some ecosystem contains wolves and lambs and the number of wolves decreases, the death rate of the lambs will go down as well. This theory was firstly formulated by Johan de Kleer, who analyzed an object moving on a roller coaster. The theory of qualitative reasoning is applied in many spheres such as physics, biology, engineering, ecology, etc. It serves as the basis for many practical programs, analogical mapping, text understanding.
Challenges in automating commonsense reasoning
As of 2014, there are some commercial systems trying to make the use of commonsense reasoning significant. However, they use statistical information as a proxy for commonsense knowledge, where reasoning is absent. Current programs manipulate individual words, but they don't attempt or offer further understanding. According to Ernest Davis and Gary Marcus, five major obstacles interfere with the producing of a satisfactory "commonsense reasoner".
- First, some of the domains that are involved in commonsense reasoning are only partly understood. Individuals are far from a comprehensive understanding of domains such as communication and knowledge, interpersonal interactions or physical processes.
- Second, situations that seem easily predicted or assumed about could have logical complexity, which humans’ commonsense knowledge does not cover. Some aspects of similar situations are studied and are well understood, but there are many relations that are unknown, even in principle and how they could be represented in a form that is usable by computers.
- Third, commonsense reasoning involves plausible reasoning. It requires coming to a reasonable conclusion given what is already known. Plausible reasoning has been studied for many years and there are a lot of theories developed that include probabilistic reasoning and non-monotonic logic. It takes different forms that include using unreliable data and rules, whose conclusions are not certain sometimes.
- Fourth, there are many domains, in which a small number of examples are extremely frequent, whereas there is a vast number of highly infrequent examples.
- Fifth, when formulating presumptions it is challenging to discern and determine the level of abstraction.
Compared with humans, as of 2018 existing computer programs perform extremely poorly on modern "commonsense reasoning" benchmark tests such as the Winograd Schema Challenge. The problem of attaining human-level competency at "commonsense knowledge" tasks is considered to probably be "AI complete" (that is, solving it would require the ability to synthesize a human-level intelligence). Some researchers believe that supervised learning data is insufficient to produce an artificial general intelligence capable of commonsense reasoning, and have therefore turned to less-supervised learning techniques.
Approaches and techniques
Commonsense's reasoning study is divided into knowledge-based approaches and approaches that are based on machine learning over and using a large data corpora with limited interactions between these two types of approaches. There are also crowdsourcing approaches, attempting to construct a knowledge basis by linking the collective knowledge and the input of non-expert people. Knowledge-based approaches can be separated into approaches based on mathematical logic.
In knowledge-based approaches, the experts are analyzing the characteristics of the inferences that are required to do reasoning in a specific area or for a certain task. The knowledge-based approaches consist of mathematically grounded approaches, informal knowledge-based approaches and large-scale approaches. The mathematically grounded approaches are purely theoretical and the result is a printed paper instead of a program. The work is limited to the range of the domains and the reasoning techniques that are being reflected on. In informal knowledge-based approaches, theories of reasoning are based on anecdotal data and intuition that are results from empirical behavioral psychology. Informal approaches are common in computer programming. Two other popular techniques for extracting commonsense knowledge from Web documents involve Web mining and Crowd sourcing.
COMET (2019), which uses both the OpenAI GPT language model architecture and existing commonsense knowledge bases such as ConceptNet, claims to generate commonsense inferences at a level approaching human benchmarks. Like many other current efforts, COMET over-relies on surface language patterns and is judged to lack deep human-level understanding of many commonsense concepts. Other language-model approaches include training on visual scenes rather than just text, and training on textual descriptions of scenarios involving commonsense physics.