Synergy is an interaction or cooperation giving rise to a
whole that is greater than the simple sum of its parts (i.e., a
non-linear addition of force, energy, or effect). The term synergy comes from the Attic Greek word συνεργία synergia from synergos, συνεργός, meaning "working together". Synergy is similar in concept to emergence.
History
The words synergy and synergetic have been used in the field of physiology since at least the middle of the 19th century:
SYN'ERGY, Synergi'a, Synenergi'a, (F.) Synergie; from συν, 'with', and εργον, 'work'. A correlation or concourse of action between different organs in health; and, according to some, in disease.
- —Dunglison, Robley Medical Lexicon Blanchard and Lea, 1853
In 1896, Henri Mazel applied the term "synergy" to social psychology by writing La synergie sociale,
in which he argued that Darwinian theory failed to account of "social
synergy" or "social love", a collective evolutionary drive. The highest
civilizations were the work not only of the elite but of the masses too;
those masses must be led, however, because the crowd, a feminine and
unconscious force, cannot distinguish between good and evil.
In 1909, Lester Frank Ward defined synergy as the universal constructive principle of nature:
I have characterized the social struggle as centrifugal and social
solidarity as centripetal. Either alone is productive of evil
consequences. Struggle is essentially destructive of the social order,
while communism removes individual initiative. The one leads to
disorder, the other to degeneracy. What is not seen—the truth that has
no expounders—is that the wholesome, constructive movement consists in
the properly ordered combination and interaction of both these
principles. This is social synergy, which is a form of cosmic synergy, the universal constructive principle of nature.
- —Ward, Lester F. Glimpses of the Cosmos, volume VI (1897–1912) G. P. Putnam's Sons, 1918, p. 358
In Christian theology, synergism is the idea that salvation involves some form of cooperation between divine grace and human freedom.
A modern view of synergy in natural sciences derives from the relationship between energy and information. Synergy is manifested when the system makes the transition between the different information (i.e. order, complexity) embedded in both systems.
Abraham Maslow and John Honigmann drew attention to an important development in the cultural anthropology field which arose in lectures by Ruth Benedict
from 1941, for which the original manuscripts have been lost but the
ideas preserved in "Synergy: Some Notes of Ruth Benedict" (1969).
Descriptions and usages
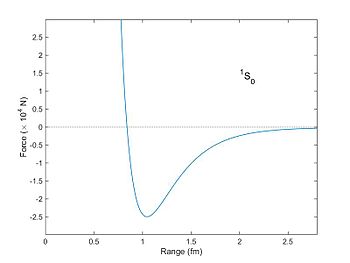
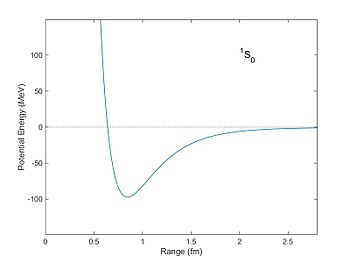
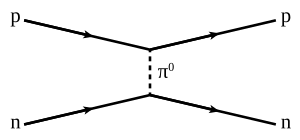
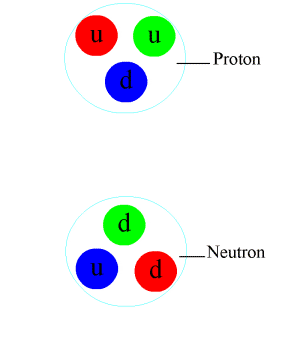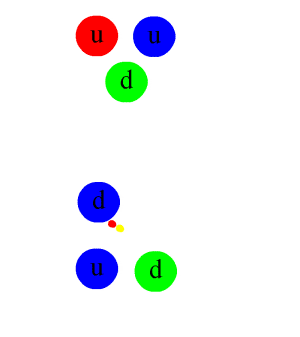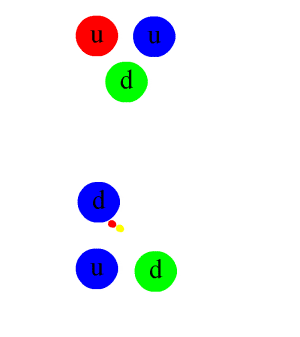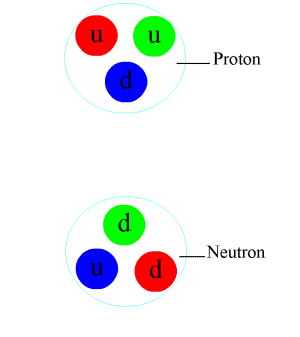
In the natural world, synergistic phenomena are ubiquitous, ranging from physics (for example, the different combinations of quarks that produce protons and neutrons)
to chemistry (a popular example is water, a compound of hydrogen and
oxygen), to the cooperative interactions among the genes in genomes, the division of labor in bacterial colonies, the synergies of scale in multicellular organisms, as well as the many different kinds of synergies produced by socially-organized groups, from honeybee colonies to wolf packs and human societies: compare stigmergy, a mechanism of indirect coordination between agents or actions that results in the self-assembly of complex systems.
Even the tools and technologies that are widespread in the natural
world represent important sources of synergistic effects. The tools that
enabled early hominins to become systematic big-game hunters is a primordial human example.
In the context of organizational behavior,
following the view that a cohesive group is more than the sum of its
parts, synergy is the ability of a group to outperform even its best
individual member. These conclusions are derived from the studies
conducted by Jay Hall on a number of laboratory-based group ranking and
prediction tasks. He found that effective groups actively looked for the
points in which they disagreed and in consequence encouraged conflicts
amongst the participants in the early stages of the discussion. In
contrast, the ineffective groups felt a need to establish a common view
quickly, used simple decision making methods such as averaging, and
focused on completing the task rather than on finding solutions they
could agree on.
In a technical context, its meaning is a construct or collection of
different elements working together to produce results not obtainable by
any of the elements alone. The elements, or parts, can include people,
hardware, software, facilities, policies, documents: all things required
to produce system-level results. The value added by the system as a
whole, beyond that contributed independently by the parts, is created
primarily by the relationship among the parts, that is, how they are
interconnected. In essence, a system constitutes a set of interrelated
components working together with a common objective: fulfilling some
designated need.
If used in a business application, synergy means that teamwork
will produce an overall better result than if each person within the
group were working toward the same goal individually. However, the
concept of group cohesion
needs to be considered. Group cohesion is that property that is
inferred from the number and strength of mutual positive attitudes among
members of the group. As the group becomes more cohesive, its
functioning is affected in a number of ways. First, the interactions and
communication between members increase. Common goals, interests and
small size all contribute to this. In addition, group member
satisfaction increases as the group provides friendship and support
against outside threats.
There are negative aspects of group cohesion that have an effect
on group decision-making and hence on group effectiveness. There are two
issues arising. The risky shift
phenomenon is the tendency of a group to make decisions that are
riskier than those that the group would have recommended individually.
Group Polarisation
is when individuals in a group begin by taking a moderate stance on an
issue regarding a common value and, after having discussed it, end up
taking a more extreme stance.
A second, potential negative consequence of group cohesion is
group think. Group think is a mode of thinking that people engage in
when they are deeply involved in cohesive group, when the members'
striving for unanimity overrides their motivation to appraise
realistically the alternative courses of action. Studying the events of
several American policy "disasters" such as the failure to anticipate
the Japanese attack on Pearl Harbor (1941) and the Bay of Pigs Invasion
fiasco (1961), Irving Janis argued that they were due to the cohesive
nature of the committees that made the relevant decisions.
That decisions made by committees lead to failure in a simple system is noted by Dr. Chris Elliot. His case study looked at IEEE-488,
an international standard set by the leading US standards body; it led
to a failure of small automation systems using the IEEE-488 standard
(which codified a proprietary communications standard HP-IB).
But the external devices used for communication were made by two
different companies, and the incompatibility between the external
devices led to a financial loss for the company. He argues that systems
will be safe only if they are designed, not if they emerge by chance.
The idea of a systemic approach is endorsed by the United Kingdom Health and Safety Executive.
The successful performance of the health and safety management depends
upon the analyzing the causes of incidents and accidents and learning
correct lessons from them. The idea is that all events (not just those
causing injuries) represent failures in control, and present an
opportunity for learning and improvement. UK Health and Safety Executive, Successful health and safety management
(1997): this book describes the principles and management practices,
which provide the basis of effective health and safety management. It
sets out the issues that need to be addressed, and can be used for
developing improvement programs, self-audit, or self-assessment. Its
message is that organizations must manage health and safety with the
same degree of expertise and to the same standards as other core
business activities, if they are to effectively control risks and
prevent harm to people.
The term synergy was refined by R. Buckminster Fuller, who analyzed some of its implications more fully and coined the term synergetics.
- A dynamic state in which combined action is favored over the difference of individual component actions.
- Behavior of whole systems unpredicted by the behavior of their parts taken separately, known as emergent behavior.
- The cooperative action of two or more stimuli (or drugs), resulting
in a different or greater response than that of the individual stimuli.
Mathematical formalizations of synergy have been proposed using information theory to rigorously define the relationships between "wholes" and "parts".
In this context, synergy is said to occur when there is information
present in the joint state of multiple variables that cannot be
extracted from the individual parts considered individually. For
example, consider the logical XOR gate. If  for three binary variables, the mutual information between any individual source and the target is 0 bit. However, the joint mutual information
for three binary variables, the mutual information between any individual source and the target is 0 bit. However, the joint mutual information  bit. There is information about the target that can only be extracted
from the joint state of the inputs considered jointly, and not any
others.
bit. There is information about the target that can only be extracted
from the joint state of the inputs considered jointly, and not any
others.
There is, thus far, no universal agreement on how synergy can
best be quantified, with different approaches that decompose information
into redundant, unique, and synergistic components appearing in the
literature.
Despite the lack of universal agreement, information-theoretic
approaches to statistical synergy have been applied to diverse fields,
including climatology, neuroscience sociology, and machine learning Synergy has also been proposed as a possible foundation on which to build a mathematically robust definition of emergence in complex systems and may be relevant to formal theories of consciousness.
Biological sciences
Synergy of various kinds has been advanced by Peter Corning
as a causal agency that can explain the progressive evolution of
complexity in living systems over the course of time. According to the
Synergism Hypothesis, synergistic effects have been the drivers of
cooperative relationships of all kinds and at all levels in living
systems. The thesis, in a nutshell, is that synergistic effects have
often provided functional advantages (economic benefits) in relation to
survival and reproduction that have been favored by natural selection.
The cooperating parts, elements, or individuals become, in effect,
functional "units" of selection in evolutionary change.
Similarly, environmental systems may react in a non-linear way to
perturbations, such as climate change, so that the outcome may be
greater than the sum of the individual component alterations.
Synergistic responses are a complicating factor in environmental
modeling.
Pest synergy
Pest synergy would occur in a biological host organism population, where, for example, the introduction of parasite
A may cause 10% fatalities, and parasite B may also cause 10% loss.
When both parasites are present, the losses would normally be expected
to total less than 20%, yet, in some cases, losses are significantly
greater. In such cases, it is said that the parasites in combination
have a synergistic effect.
Drug synergy
Mechanisms that may be involved in the development of synergistic effects include:
- Effect on the same cellular system (e.g. two different antibiotics like a penicillin and an aminoglycoside; penicillins damage the cell wall of gram-positive bacteria and improve the penetration of aminoglycosides).
- Bioavailability (e.g. ayahuasca (or pharmahuasca) consists of DMT combined with MAOIs that interfere with the action of the MAO enzyme and stop the breakdown of chemical compounds such as DMT).
- Reduced risk for substance abuse (e.g. lisdexamfetamine, which is a combination of the amino acid L-lysine, attached to dextroamphetamine, may have a lower liability for abuse as a recreational drug)
- Increased potency (e.g. as with other NSAIDs, combinations of aspirin and caffeine provide slightly greater pain relief than aspirin alone).
- Prevention or delay of degradation in the body (e.g. the antibiotic Ciprofloxacin inhibits the metabolism of Theophylline).[30]: 931
- Slowdown of excretion (e.g. Probenecid delays the renal excretion of Penicillin and thus prolongs its effect).
- Anticounteractive action: for example, the effect of oxaliplatin and irinotecan. Oxaliplatin intercalates DNA, thereby preventing the cell from replicating DNA. Irinotecan inhibits topoisomerase 1, consequently the cytostatic effect is increased.
- Effect on the same receptor but different sites (e.g. the
coadministration of benzodiazepines and barbiturates, both act by
enhancing the action of GABA on GABAA receptors, but
benzodiazepines increase the frequency of channel opening, whilst
barbiturates increase the channel closing time, making these two drugs
dramatically enhance GABAergic neurotransmission).
- In addition to the chemical nature of the drug itself, the topology
of the chemical reaction network that connect the two targets determines
the type of drug-drug interaction.
More mechanisms are described in an exhaustive 2009 review.
Toxicological synergy
Toxicological
synergy is of concern to the public and regulatory agencies because
chemicals individually considered safe might pose unacceptable health or
ecological risk in combination. Articles in scientific and lay journals
include many definitions of chemical or toxicological synergy, often
vague or in conflict with each other. Because toxic interactions are
defined relative to the expectation under "no interaction", a
determination of synergy (or antagonism) depends on what is meant by "no
interaction". The United States Environmental Protection Agency has one of the more detailed and precise definitions of toxic interaction, designed to facilitate risk assessment.
In their guidance documents, the no-interaction default assumption is
dose addition, so synergy means a mixture response that exceeds that
predicted from dose addition. The EPA emphasizes that synergy does not
always make a mixture dangerous, nor does antagonism always make the
mixture safe; each depends on the predicted risk under dose addition.
For example, a consequence of pesticide use is the risk of health effects. During the registration of pesticides in the United States
exhaustive tests are performed to discern health effects on humans at
various exposure levels. A regulatory upper limit of presence in foods
is then placed on this pesticide. As long as residues in the food stay
below this regulatory level, health effects are deemed highly unlikely
and the food is considered safe to consume.
However, in normal agricultural practice, it is rare to use only a
single pesticide. During the production of a crop, several different
materials may be used. Each of them has had determined a regulatory
level at which they would be considered individually safe. In many
cases, a commercial pesticide is itself a combination of several
chemical agents, and thus the safe levels actually represent levels of
the mixture. In contrast, a combination created by the end user, such as
a farmer, has rarely been tested in that combination. The potential for
synergy is then unknown or estimated from data on similar combinations.
This lack of information also applies to many of the chemical
combinations to which humans are exposed, including residues in food,
indoor air contaminants, and occupational exposures to chemicals. Some
groups think that the rising rates of cancer, asthma, and other health
problems may be caused by these combination exposures; others have
alternative explanations. This question will likely be answered only
after years of exposure by the population in general and research on
chemical toxicity, usually performed on animals. Examples of pesticide
synergists include Piperonyl butoxide and MGK 264.
Human synergy
Synergy
exists in individual and social interactions among humans, with some
arguing that social cooperation cannot be requires synergy to continue.
One way of quantifying synergy in human social groups is via energy
use, where larger groups of humans (i.e., cities) use energy more
efficiently that smaller groups of humans.
Human synergy can also occur on a smaller scale, like when
individuals huddle together for warmth or in workplaces where labor
specialization increase efficiencies.
When synergy occurs in the work place, the individuals involved
get to work in a positive and supportive working environment. When
individuals get to work in environments such as these, the company reaps
the benefits. The authors of Creating the Best Workplace on Earth
Rob Goffee and Gareth Jones, state that "highly engaged employees are,
on average, 50% more likely to exceed expectations that the
least-engaged workers. And companies with highly engaged people
outperform firms with the most disengaged folks- by 54% in employee retention, by 89% in customer satisfaction, and by fourfold in revenue growth.
Also, those that are able to be open about their views on the company,
and have confidence that they will be heard, are likely to be a more
organized employee who helps his/ her fellow team members succeed.
Human interaction with technology can also increase synergy. Organismic computing is an approach to improving group efficacy by increasing synergy in human groups via technological means.
Theological synergism
In Christian theology, synergism is the belief that salvation involves a cooperation between divine grace and human freedom. Eastern Orthodox
theology, in particular, uses the term "synergy" to describe this
relationship, drawing on biblical language: "in Paul's words, 'We are
fellow-workers (synergoi) with God' (1 Corinthians iii, 9)".
Corporate synergy
Corporate synergy
occurs when corporations interact congruently. A corporate synergy
refers to a financial benefit that a corporation expects to realize when
it merges with or acquires
another corporation. This type of synergy is a nearly ubiquitous
feature of a corporate acquisition and is a negotiating point between
the buyer and seller that impacts the final price both parties agree to.
There are distinct types of corporate synergies, as follows.
Marketing
A marketing synergy refers to the use of information campaigns, studies, and scientific discovery or experimentation for research and development. This promotes the sale of products for varied use or off-market sales as well as development of marketing tools and in several cases exaggeration of effects. It is also often a meaningless buzzword used by corporate leaders.
Microsoft Word offers "cooperation" as a refinement suggestion to the word "synergy."
Revenue
A revenue
synergy refers to the opportunity of a combined corporate entity to
generate more revenue than its two predecessor stand-alone companies
would be able to generate. For example, if company A sells product X
through its sales force, company B sells product Y, and company A
decides to buy company B, then the new company could use each
salesperson to sell products X and Y, thereby increasing the revenue
that each salesperson generates for the company.
In media revenue, synergy is the promotion and sale of a product throughout the various subsidiaries of a media conglomerate, e.g. films, soundtracks, or video games.
Financial
Financial
synergy gained by the combined firm is a result of number of benefits
which flow to the entity as a consequence of acquisition and merger.
These benefits may be:
Cash slack
This
is when a firm having a number of cash extensive projects acquires a
firm which is cash-rich, thus enabling the new combined firm to enjoy
the profits from investing the cash of one firm in the projects of the
other.
Debt capacity
If two firms have no or little capacity to carry debt
before individually, it is possible for them to join and gain the
capacity to carry the debt through decreased gearing (leverage). This
creates value for the firm, as debt is thought to be a cheaper source of
finance.
Tax benefits
It is possible for one firm to have unused tax benefits
which might be offset against the profits of another after combination,
thus resulting in less tax being paid. However this greatly depends on
the tax law of the country.
Management
Synergy in management and in relation to teamwork refers to the combined effort of individuals as participants of the team.
The condition that exists when the organization's parts interact to
produce a joint effect that is greater than the sum of the parts acting
alone. Positive or negative synergies can exist. In these cases,
positive synergy has positive effects such as improved efficiency in
operations, greater exploitation of opportunities, and improved
utilization of resources. Negative synergy on the other hand has
negative effects such as: reduced efficiency of operations, decrease in
quality, underutilization of resources and disequilibrium with the
external environment.
Cost
A
cost synergy refers to the opportunity of a combined corporate entity to
reduce or eliminate expenses associated with running a business. Cost
synergies are realized by eliminating positions that are viewed as
duplicate within the merged entity.
Examples include the headquarters office of one of the predecessor
companies, certain executives, the human resources department, or other
employees of the predecessor companies. This is related to the economic
concept of economies of scale.
Synergistic action in economy
The
synergistic action of the economic players lies within the economic
phenomenon's profundity. The synergistic action gives different
dimensions to competitiveness, strategy and network identity becoming an
unconventional "weapon" which belongs to those who exploit the economic
systems' potential in depth.
Synergistic determinants
The
synergistic gravity equation (SYNGEq), according to its complex
"title", represents a synthesis of the endogenous and exogenous factors
which determine the private and non-private economic decision makers to
call to actions of synergistic exploitation of the economic network in
which they operate. That is to say, SYNGEq constitutes a big picture of
the factors/motivations which determine the entrepreneurs to contour an
active synergistic network. SYNGEq includes both factors which character
is changing over time (such as the competitive conditions), as well as
classics factors, such as the imperative of the access to resources of
the collaboration and the quick answers. The synergistic gravity
equation (SINGEq) comes to be represented by the formula:
ΣSYN.Act = ΣR-*I(CRed+COOP++AUnimit.)*V(Cust.+Info.)*cc
where:
- ΣSYN.Act = the sum of the synergistic actions adopted (by the economic actor)
- Σ R- = the amount of unpurchased but necessary resources
- ICRed = the imperative for cost reductions
- ICOOP+ = the imperative for deep cooperation (functional interdependence)
- IAUnimit. = the imperative for purchasing unimitable competitive advantages (for the economic actor)
- VCust = the necessity of customer value in purchasing future profits
and competitive advantages VInfo = the necessity of informational value
in purchasing future profits and competitive advantages
- cc = the specific competitive conditions in which the economic actor operates
Synergistic networks and systems
The
synergistic network represents an integrated part of the economic
system which, through the coordination and control functions (of the
undertaken economic actions), agrees synergies. The networks which
promote synergistic actions can be divided in horizontal synergistic
networks and vertical synergistic networks.
Synergy effects
The
synergy effects are difficult (even impossible) to imitate by
competitors and difficult to reproduce by their authors because these
effects depend on the combination of factors with time-varying
characteristics. The synergy effects are often called "synergistic
benefits", representing the direct and implied result of the
developed/adopted synergistic actions.
Computers
Synergy can also be defined as the combination of human strengths and computer strengths, such as advanced chess. Computers can process data much more quickly than humans, but lack the ability to respond meaningfully to arbitrary stimuli.
Synergy in literature
Etymologically,
the "synergy" term was first used around 1600, deriving from the Greek
word "synergos", which means "to work together" or "to cooperate". If
during this period the synergy concept was mainly used in the
theological field (describing "the cooperation of human effort with
divine will"), in the 19th and 20th centuries, "synergy" was promoted in
physics and biochemistry, being implemented in the study of the open
economic systems only in the 1960 and 1970s.
In 1938, J. R. R. Tolkien wrote an essay titled On Fairy Stores, delivered at an Andrew Lang Lecture, and reprinted in his book, The Tolkien Reader, published in 1966. In it, he made two references to synergy, although he did not use that term. He wrote:
Faerie cannot be caught in a net of words; for it is one of its
qualities to be indescribable, though not imperceptible. It has many
ingredients, but analysis will not necessarily discover the secret of
the whole.
And more succinctly, in a footnote, about the "part of producing the web of an intricate story", he wrote:
It is indeed easier to unravel a single thread — an incident, a name, a motive — than to trace the history of any picture
defined by many threads. For with the picture in the tapestry a new
element has come in: the picture is greater than, and not explained by,
the sum of the component threads.
The book "Synergy"
Synergy, a book: DION, Eric (2017), Synergy; A Theoretical Model of Canada's Comprehensive Approach, iUniverse, 308 pp.
The
informational synergies which can be applied also in media involve a
compression of transmission, access and use of information's time, the
flows, circuits and means of handling information being based on a
complementary, integrated, transparent and coordinated use of knowledge.
In media economics, synergy is the promotion and sale of a
product (and all its versions) throughout the various subsidiaries of a
media conglomerate, e.g. films, soundtracks or video games. Walt Disney pioneered synergistic marketing techniques in the 1930s by granting dozens of firms the right to use his Mickey Mouse
character in products and ads, and continued to market Disney media
through licensing arrangements. These products can help advertise the
film itself and thus help to increase the film's sales. For example, the
Spider-Man films had toys of webshooters and figures of the characters made, as well as posters and games. The NBC sitcom 30 Rock often shows the power of synergy, while also poking fun at the use of the term in the corporate world. There are also different forms of synergy in popular card games like Magic: The Gathering, Yu-Gi-Oh!, Cardfight!! Vanguard, and Future Card Buddyfight.
















































![{\displaystyle {\mathcal {L}}_{\mathrm {C} }=-{\frac {g}{\ {\sqrt {2\;}}\ }}\ \left[\ {\overline {u}}_{i}\ \gamma ^{\mu }\ {\frac {\ 1-\gamma ^{5}\ }{2}}\;M_{ij}^{\mathrm {CKM} }\ d_{j}+{\overline {\nu }}_{i}\ \gamma ^{\mu }\;{\frac {\ 1-\gamma ^{5}\ }{2}}\;e_{i}\ \right]\ W_{\mu }^{+}+\mathrm {h.c.} ~,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a58fb2388e4f81affcfbb2f9137be3fc21c01d32)







![{\displaystyle {\mathcal {L}}_{\mathrm {WWV} }=-i\ g\ \left[\;\left(\ W_{\mu \nu }^{+}\ W^{-\mu }-W^{+\mu }\ W_{\mu \nu }^{-}\ \right)\left(\ A^{\nu }\ \sin \theta _{\mathrm {W} }-Z^{\nu }\ \cos \theta _{\mathrm {W} }\ \right)+W_{\nu }^{-}\ W_{\mu }^{+}\ \left(\ A^{\mu \nu }\ \sin \theta _{\mathrm {W} }-Z^{\mu \nu }\ \cos \theta _{\mathrm {W} }\ \right)\;\right]~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a692b930d152ed1c16bd24ebede10eb0a7f7c2b)

![{\displaystyle {\begin{aligned}{\mathcal {L}}_{\mathrm {WWVV} }=-{\frac {\ g^{2}\ }{4}}\ {\Biggl \{}\ &{\Bigl [}\ 2\ W_{\mu }^{+}\ W^{-\mu }+(\ A_{\mu }\ \sin \theta _{\mathrm {W} }-Z_{\mu }\ \cos \theta _{\mathrm {W} }\ )^{2}\ {\Bigr ]}^{2}\\&-{\Bigl [}\ W_{\mu }^{+}\ W_{\nu }^{-}+W_{\nu }^{+}\ W_{\mu }^{-}+\left(\ A_{\mu }\ \sin \theta _{\mathrm {W} }-Z_{\mu }\ \cos \theta _{\mathrm {W} }\ \right)\left(\ A_{\nu }\ \sin \theta _{\mathrm {W} }-Z_{\nu }\ \cos \theta _{\mathrm {W} }\ \right)\ {\Bigr ]}^{2}\,{\Biggr \}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7a413ef9a695a06d5c93067c2745e6bfe3d1a3)