From Wikipedia, the free encyclopedia
In
physics,
string theory is a
theoretical framework in which the
point-like particles of
particle physics are replaced by
one-dimensional objects called
strings.
It describes how these strings propagate through space and interact
with each other. On distance scales larger than the string scale, a
string looks just like an ordinary particle, with its
mass,
charge, and other properties determined by the
vibrational state of the string. In string theory, one of the many vibrational states of the string corresponds to the
graviton, a
quantum mechanical particle that carries
gravitational force. Thus string theory is a theory of
quantum gravity.
String theory is a broad and varied subject that attempts to address a number of deep questions of
fundamental physics. String theory has been applied to a variety of problems in
black hole physics, early universe
cosmology,
nuclear physics, and
condensed matter physics, and it has stimulated a number of major developments in
pure mathematics. Because string theory potentially provides a unified description of gravity and particle physics, it is a candidate for a
theory of everything, a self-contained
mathematical model that describes all
fundamental forces and forms of
matter.
Despite much work on these problems, it is not known to what extent
string theory describes the real world or how much freedom the theory
allows in the choice of its details.
String theory was first studied in the late 1960s as a theory of the
strong nuclear force, before being abandoned in favor of
quantum chromodynamics.
Subsequently, it was realized that the very properties that made string
theory unsuitable as a theory of nuclear physics made it a promising
candidate for a quantum theory of gravity. The earliest version of
string theory,
bosonic string theory, incorporated only the class of
particles known as
bosons. It later developed into
superstring theory, which posits a connection called
supersymmetry between bosons and the class of particles called
fermions.
Five consistent versions of superstring theory were developed before it
was conjectured in the mid-1990s that they were all different limiting
cases of a single theory in eleven dimensions known as
M-theory. In late 1997, theorists discovered an important relationship called the
AdS/CFT correspondence, which relates string theory to another type of physical theory called a
quantum field theory.
One of the challenges of string theory is that the full theory does
not have a satisfactory definition in all circumstances. Another issue
is that the theory is thought to describe an enormous
landscape
of possible universes, and this has complicated efforts to develop
theories of particle physics based on string theory. These issues have
led some in the community to criticize these approaches to physics and
question the value of continued research on string theory unification.
Fundamentals
The fundamental objects of string theory are open and closed
string models.
In the twentieth century, two theoretical frameworks emerged for formulating the laws of physics. The first is
Albert Einstein's
general theory of relativity, a theory that explains the force of
gravity and the structure of space and time. The other is
quantum mechanics which is a completely different formulation to describe physical phenomena using the known
probability
principles. By the late 1970s, these two frameworks had proven to be
sufficient to explain most of the observed features of the
universe, from
elementary particles to
atoms to the evolution of stars and the universe as a whole.
[1]
In spite of these successes, there are still many problems that
remain to be solved. One of the deepest problems in modern physics is
the problem of
quantum gravity.
[1] The general theory of relativity is formulated within the framework of
classical physics, whereas the other
fundamental forces
are described within the framework of quantum mechanics. A quantum
theory of gravity is needed in order to reconcile general relativity
with the principles of quantum mechanics, but difficulties arise when
one attempts to apply the usual prescriptions of quantum theory to the
force of gravity.
[2]
In addition to the problem of developing a consistent theory of quantum
gravity, there are many other fundamental problems in the physics of
atomic nuclei,
black holes, and the early universe.
[a]
String theory is a
theoretical framework that attempts to address these questions and many others. The starting point for string theory is the idea that the
point-like particles of
particle physics can also be modeled as one-dimensional objects called
strings.
String theory describes how strings propagate through space and
interact with each other. In a given version of string theory, there is
only one kind of string, which may look like a small loop or segment of
ordinary string, and it can vibrate in different ways. On distance
scales larger than the string scale, a string will look just like an
ordinary particle, with its
mass,
charge,
and other properties determined by the vibrational state of the string. In this way, all of the different elementary particles may be viewed as
vibrating strings. In string theory, one of the vibrational states of the string gives rise to the
graviton, a quantum mechanical particle that carries gravitational force. Thus string theory is a theory of quantum gravity.
[3]
One of the main developments of the past several decades in string
theory was the discovery of certain "dualities", mathematical
transformations that identify one physical theory with another.
Physicists studying string theory have discovered a number of these
dualities between different versions of string theory, and this has led
to the conjecture that all consistent versions of string theory are
subsumed in a single framework known as
M-theory.
[4]
Studies of string theory have also yielded a number of results on the
nature of black holes and the gravitational interaction. There are
certain paradoxes that arise when one attempts to understand the quantum
aspects of black holes, and work on string theory has attempted to
clarify these issues. In late 1997 this line of work culminated in the
discovery of the
anti-de Sitter/conformal field theory correspondence or AdS/CFT.
[5]
This is a theoretical result which relates string theory to other
physical theories which are better understood theoretically. The AdS/CFT
correspondence has implications for the study of black holes and
quantum gravity, and it has been applied to other subjects, including
nuclear[6] and
condensed matter physics.
[7][8]
Since string theory incorporates all of the fundamental interactions,
including gravity, many physicists hope that it fully describes our
universe, making it a
theory of everything.
One of the goals of current research in string theory is to find a
solution of the theory that reproduces the observed spectrum of
elementary particles, with a small
cosmological constant, containing
dark matter and a plausible mechanism for
cosmic inflation.
While there has been progress toward these goals, it is not known to
what extent string theory describes the real world or how much freedom
the theory allows in the choice of details.
[9]
One of the challenges of string theory is that the full theory does
not have a satisfactory definition in all circumstances. The scattering
of strings is most straightforwardly defined using the techniques of
perturbation theory, but it is not known in general how to define string theory
nonperturbatively.
[10] It is also not clear whether there is any principle by which string theory selects its
vacuum state, the physical state that determines the properties of our universe.
[11]
These problems have led some in the community to criticize these
approaches to the unification of physics and question the value of
continued research on these problems.
[12]
Strings
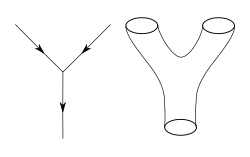
The application of quantum mechanics to physical objects such as the
electromagnetic field, which are extended in space and time, is known as
quantum field theory.
In particle physics, quantum field theories form the basis for our
understanding of elementary particles, which are modeled as excitations
in the fundamental fields.
[13]
In quantum field theory, one typically computes the probabilities of various physical events using the techniques of
perturbation theory. Developed by
Richard Feynman and others in the first half of the twentieth century, perturbative quantum field theory uses special diagrams called
Feynman diagrams to organize computations. One imagines that these diagrams depict the paths of point-like particles and their interactions.
[13]
The starting point for string theory is the idea that the point-like
particles of quantum field theory can also be modeled as one-dimensional
objects called strings.
[14]
The interaction of strings is most straightforwardly defined by
generalizing the perturbation theory used in ordinary quantum field
theory. At the level of Feynman diagrams, this means replacing the
one-dimensional diagram representing the path of a point particle by a
two-dimensional surface representing the motion of a string.
[15]
Unlike in quantum field theory, string theory does not have a full
non-perturbative definition, so many of the theoretical questions that
physicists would like to answer remain out of reach.
[16]
In theories of particle physics based on string theory, the
characteristic length scale of strings is assumed to be on the order of
the
Planck length, or
10−35 meters, the scale at which the effects of quantum gravity are believed to become significant.
[15]
On much larger length scales, such as the scales visible in physics
laboratories, such objects would be indistinguishable from
zero-dimensional point particles, and the vibrational state of the
string would determine the type of particle. One of the vibrational
states of a string corresponds to the graviton, a quantum mechanical
particle that carries the gravitational force.
[3]
The original version of string theory was
bosonic string theory, but this version described only
bosons, a class of particles which transmit forces between the matter particles, or
fermions. Bosonic string theory was eventually superseded by theories called
superstring theories. These theories describe both bosons and fermions, and they incorporate a theoretical idea called
supersymmetry.
This is a mathematical relation that exists in certain physical
theories between the bosons and fermions. In theories with
supersymmetry, each boson has a counterpart which is a fermion, and vice
versa.
[17]
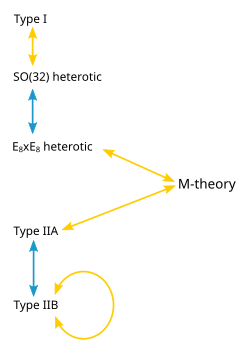
There are several versions of superstring theory:
type I,
type IIA,
type IIB, and two flavors of
heterotic string theory (
SO(32) and
E8×E8). The different theories allow different types of strings, and the particles that arise at low energies exhibit different
symmetries.
For example, the type I theory includes both open strings (which are
segments with endpoints) and closed strings (which form closed loops),
while types IIA, IIB and heterotic include only closed strings.
[18]
An example of
compactification: At large distances, a two dimensional surface with one circular dimension looks one-dimensional.
In everyday life, there are three familiar dimensions of space:
height, width and length. Einstein's general theory of relativity treats
time as a dimension on par with the three spatial dimensions; in
general relativity, space and time are not modeled as separate entities
but are instead unified to a four-dimensional
spacetime. In this framework, the phenomenon of gravity is viewed as a consequence of the geometry of spacetime.
[19]
In spite of the fact that the universe is well described by
four-dimensional spacetime, there are several reasons why physicists
consider theories in other dimensions. In some cases, by modeling
spacetime in a different number of dimensions, a theory becomes more
mathematically tractable, and one can perform calculations and gain
general insights more easily.
[b]
There are also situations where theories in two or three spacetime
dimensions are useful for describing phenomena in condensed matter
physics.
[20]
Finally, there exist scenarios in which there could actually be more
than four dimensions of spacetime which have nonetheless managed to
escape detection.
[21]
One notable feature of string theories is that these theories require
extra dimensions
of spacetime for their mathematical consistency. In bosonic string
theory, spacetime is 26-dimensional, while in superstring theory it is
10-dimensional, and in
M-theory
it is 11-dimensional. In order to describe real physical phenomena
using string theory, one must therefore imagine scenarios in which these
extra dimensions would not be observed in experiments.
[22]
Compactification
is one way of modifying the number of dimensions in a physical theory.
In compactification, some of the extra dimensions are assumed to "close
up" on themselves to form circles.
[23]
In the limit where these curled up dimensions become very small, one
obtains a theory in which spacetime has effectively a lower number of
dimensions. A standard analogy for this is to consider a
multidimensional object such as a garden hose. If the hose is viewed
from a sufficient distance, it appears to have only one dimension, its
length. However, as one approaches the hose, one discovers that it
contains a second dimension, its circumference. Thus, an ant crawling on
the surface of the hose would move in two dimensions.
[24]
Compactification can be used to construct models in which spacetime
is effectively four-dimensional. However, not every way of compactifying
the extra dimensions produces a model with the right properties to
describe nature. In a viable model of particle physics, the compact
extra dimensions must be shaped like a
Calabi–Yau manifold.
[23] A Calabi–Yau manifold is a special
space which is typically taken to be six-dimensional in applications to string theory. It is named after mathematicians
Eugenio Calabi and
Shing-Tung Yau.
[25]
Another approach to reducing the number of dimensions is the so-called
brane-world
scenario. In this approach, physicists assume that the observable
universe is a four-dimensional subspace of a higher dimensional space.
In such models, the force-carrying bosons of particle physics arise from
open strings with endpoints attached to the four-dimensional subspace,
while gravity arises from closed strings propagating through the larger
ambient space. This idea plays an important role in attempts to develop
models of real world physics based on string theory, and it provides a
natural explanation for the weakness of gravity compared to the other
fundamental forces.
[26]
Dualities
A diagram of string theory dualities. Yellow arrows indicate
S-duality. Blue arrows indicate
T-duality.
One notable fact about string theory is that the different versions
of the theory all turn out to be related in highly nontrivial ways. One
of the relationships that can exist between different string theories is
called
S-duality.
This is a relationship which says that a collection of strongly
interacting particles in one theory can, in some cases, be viewed as a
collection of weakly interacting particles in a completely different
theory. Roughly speaking, a collection of particles is said to be
strongly interacting if they combine and decay often and weakly
interacting if they do so infrequently. Type I string theory turns out
to be equivalent by S-duality to the
SO(32) heterotic string theory. Similarly, type IIB string theory is related to itself in a nontrivial way by S-duality.
[27]
Another relationship between different string theories is
T-duality.
Here one considers strings propagating around a circular extra
dimension. T-duality states that a string propagating around a circle of
radius
R is equivalent to a string propagating around a circle of radius
1/R
in the sense that all observable quantities in one description are
identified with quantities in the dual description. For example, a
string has
momentum
as it propagates around a circle, and it can also wind around the
circle one or more times. The number of times the string winds around a
circle is called the
winding number. If a string has momentum
p and winding number
n in one description, it will have momentum
n and winding number
p
in the dual description. For example, type IIA string theory is
equivalent to type IIB string theory via T-duality, and the two versions
of heterotic string theory are also related by T-duality.
[27]
In general, the term
duality refers to a situation where two seemingly different
physical systems turn out to be equivalent in a nontrivial way. Two theories related by a duality need not be string theories. For example,
Montonen–Olive duality
is example of an S-duality relationship between quantum field theories.
The AdS/CFT correspondence is example of a duality which relates string
theory to a quantum field theory. If two theories are related by a
duality, it means that one theory can be transformed in some way so that
it ends up looking just like the other theory. The two theories are
then said to be
dual to one another under the transformation. Put
differently, the two theories are mathematically different descriptions
of the same phenomena.
[28]
Branes

Open strings attached to a pair of
D-branes.
In string theory and other related theories, a
brane
is a physical object that generalizes the notion of a point particle to
higher dimensions. For instance, a point particle can be viewed as a
brane of dimension zero, while a string can be viewed as a brane of
dimension one. It is also possible to consider higher-dimensional
branes. In dimension
p, these are called
p-branes. The word brane comes from the word "membrane" which refers to a two-dimensional brane.
[29]
Branes are dynamical objects which can propagate through spacetime
according to the rules of quantum mechanics. They have mass and can have
other attributes such as charge. A
p-brane sweeps out a (
p+1)-dimensional volume in spacetime called its
worldvolume. Physicists often study
fields analogous to the electromagnetic field which live on the worldvolume of a brane.
[29]
In string theory,
D-branes
are an important class of branes that arise when one considers open
strings. As an open string propagates through spacetime, its endpoints
are required to lie on a D-brane. The letter "D" in D-brane refers to a
certain mathematical condition on the system known as the
Dirichlet boundary condition.
The study of D-branes in string theory has led to important results
such as the AdS/CFT correspondence, which has shed light on many
problems in quantum field theory.
[30]
Branes are frequently studied from a purely mathematical point of view, and they are described as objects of certain
categories, such as the
derived category of
coherent sheaves on a
complex algebraic variety, or the
Fukaya category of a
symplectic manifold.
[31]
The connection between the physical notion of a brane and the
mathematical notion of a category has led to important mathematical
insights in the fields of
algebraic and
symplectic geometry [32] and
representation theory.
[33]
M-theory
Prior to 1995, theorists believed that there were five consistent
versions of superstring theory (type I, type IIA, type IIB, and two
versions of heterotic string theory). This understanding changed in 1995
when
Edward Witten
suggested that the five theories were just special limiting cases of an
eleven-dimensional theory called M-theory. Witten's conjecture was
based on the work of a number of other physicists, including
Ashoke Sen,
Chris Hull,
Paul Townsend, and
Michael Duff. His announcement led to a flurry of research activity now known as the
second superstring revolution.
[34]
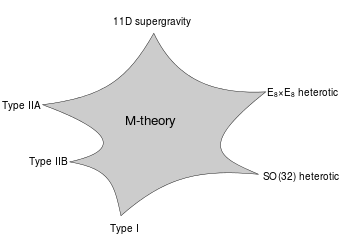
Unification of superstring theories
A schematic illustration of the relationship between
M-theory, the five
superstring theories, and eleven-dimensional
supergravity.
The shaded region represents a family of different physical scenarios
that are possible in M-theory. In certain limiting cases corresponding
to the cusps, it is natural to describe the physics using one of the six
theories labeled there.
In the 1970s, many physicists became interested in
supergravity
theories, which combine general relativity with supersymmetry. Whereas
general relativity makes sense in any number of dimensions, supergravity
places an upper limit on the number of dimensions.
[35] In 1978, work by
Werner Nahm showed that the maximum spacetime dimension in which one can formulate a consistent supersymmetric theory is eleven.
[36] In the same year,
Eugene Cremmer,
Bernard Julia, and
Joel Scherk of the
École Normale Supérieure
showed that supergravity not only permits up to eleven dimensions but
is in fact most elegant in this maximal number of dimensions.
[37][38]
Initially, many physicists hoped that by compactifying
eleven-dimensional supergravity, it might be possible to construct
realistic models of our four-dimensional world. The hope was that such
models would provide a unified description of the four fundamental
forces of nature: electromagnetism, the
strong and
weak nuclear forces,
and gravity. Interest in eleven-dimensional supergravity soon waned as
various flaws in this scheme were discovered. One of the problems was
that the laws of physics appear to distinguish between clockwise and
counterclockwise, a phenomenon known as
chirality. Edward Witten and others observed this chirality property cannot be readily derived by compactifying from eleven dimensions.
[38]
In the
first superstring revolution
in 1984, many physicists turned to string theory as a unified theory of
particle physics and quantum gravity. Unlike supergravity theory,
string theory was able to accommodate the chirality of the standard
model, and it provided a theory of gravity consistent with quantum
effects.
[38]
Another feature of string theory that many physicists were drawn to in
the 1980s and 1990s was its high degree of uniqueness. In ordinary
particle theories, one can consider any collection of elementary
particles whose classical behavior is described by an arbitrary
Lagrangian. In string theory, the possibilities are much more constrained: by the
1990s, physicists had argued that there were only five consistent
supersymmetric versions of the theory.
[38]
Although there were only a handful of consistent superstring
theories, it remained a mystery why there was not just one consistent
formulation.
[38]
However, as physicists began to examine string theory more closely,
they realized that these theories are related in intricate and
nontrivial ways. They found that a system of strongly interacting
strings can, in some cases, be viewed as a system of weakly interacting
strings. This phenomenon is known as S-duality. It was studied by Ashoke
Sen in the context of heterotic strings in four dimensions
[39][40] and by Chris Hull and Paul Townsend in the context of the type IIB theory.
[41]
Theorists also found that different string theories may be related by
T-duality. This duality implies that strings propagating on completely
different spacetime geometries may be physically equivalent.
[42]
At around the same time, as many physicists were studying the
properties of strings, a small group of physicists was examining the
possible applications of higher dimensional objects. In 1987, Eric
Bergshoeff, Ergin Sezgin, and Paul Townsend showed that
eleven-dimensional supergravity includes two-dimensional branes.
[43]
Intuitively, these objects look like sheets or membranes propagating
through the eleven-dimensional spacetime. Shortly after this discovery,
Michael Duff,
Paul Howe, Takeo Inami, and Kellogg Stelle considered a particular
compactification of eleven-dimensional supergravity with one of the
dimensions curled up into a circle.
[44]
In this setting, one can imagine the membrane wrapping around the
circular dimension. If the radius of the circle is sufficiently small,
then this membrane looks just like a string in ten-dimensional
spacetime. In fact, Duff and his collaborators showed that this
construction reproduces exactly the strings appearing in type IIA
superstring theory.
[45]
Speaking at a string theory conference in 1995, Edward Witten made
the surprising suggestion that all five superstring theories were in
fact just different limiting cases of a single theory in eleven
spacetime dimensions. Witten's announcement drew together all of the
previous results on S- and T-duality and the appearance of higher
dimensional branes in string theory.
[46]
In the months following Witten's announcement, hundreds of new papers
appeared on the Internet confirming different parts of his proposal.
[47] Today this flurry of work is known as the second superstring revolution.
[48]
Initially, some physicists suggested that the new theory was a
fundamental theory of membranes, but Witten was skeptical of the role of
membranes in the theory. In a paper from 1996, Hořava and Witten wrote
"As it has been proposed that the eleven-dimensional theory is a
supermembrane theory but there are some reasons to doubt that
interpretation, we will non-committally call it the M-theory, leaving to
the future the relation of M to membranes."
[49] In the absence of an understanding of the true meaning and structure of M-theory, Witten has suggested that the
M
should stand for "magic", "mystery", or "membrane" according to taste,
and the true meaning of the title should be decided when a more
fundamental formulation of the theory is known.
[50]
Matrix theory
In mathematics, a
matrix is a rectangular array of numbers or other data. In physics, a
matrix model
is a particular kind of physical theory whose mathematical formulation
involves the notion of a matrix in an important way. A matrix model
describes the behavior of a set of matrices within the framework of
quantum mechanics.
[51]
One important example of a matrix model is the BFSS matrix model proposed by
Tom Banks,
Willy Fischler,
Stephen Shenker, and
Leonard Susskind
in 1997. This theory describes the behavior of a set of nine large
matrices. In their original paper, these authors showed, among other
things, that the low energy limit of this matrix model is described by
eleven-dimensional supergravity. These calculations led them to propose
that the BFSS matrix model is exactly equivalent to M-theory. The BFSS
matrix model can therefore be used as a prototype for a correct
formulation of M-theory and a tool for investigating the properties of
M-theory in a relatively simple setting.
[51]
The development of the matrix model formulation of M-theory has led
physicists to consider various connections between string theory and a
branch of mathematics called
noncommutative geometry. This subject is a generalization of ordinary geometry in which mathematicians define new geometric notions using tools from
noncommutative algebra.
[52] In a paper from 1998,
Alain Connes,
Michael R. Douglas, and
Albert Schwarz showed that some aspects of matrix models and M-theory are described by a
noncommutative quantum field theory, a special kind of physical theory in which spacetime is described mathematically using noncommutative geometry.
[53]
This established a link between matrix models and M-theory on the one
hand, and noncommutative geometry on the other hand. It quickly led to
the discovery of other important links between noncommutative geometry
and various physical theories.
[54][55]
Black holes
In general relativity, a black hole is defined as a region of
spacetime in which the gravitational field is so strong that no particle
or radiation can escape. In the currently accepted models of stellar
evolution, black holes are thought to arise when massive stars undergo
gravitational collapse, and many
galaxies are thought to contain
supermassive black holes
at their centers. Black holes are also important for theoretical
reasons, as they present profound challenges for theorists attempting to
understand the quantum aspects of gravity. String theory has proved to
be an important tool for investigating the theoretical properties of
black holes because it provides a framework in which theorists can study
their
thermodynamics.
[56]
Bekenstein–Hawking formula
In the branch of physics called
statistical mechanics,
entropy
is a measure of the randomness or disorder of a physical system. This
concept was studied in the 1870s by the Austrian physicist
Ludwig Boltzmann, who showed that the
thermodynamic properties of a
gas could be derived from the combined properties of its many constituent
molecules.
Boltzmann argued that by averaging the behaviors of all the different
molecules in a gas, one can understand macroscopic properties such as
volume, temperature, and pressure. In addition, this perspective led him
to give a precise definition of entropy as the
natural logarithm of the number of different states of the molecules (also called
microstates) that give rise to the same macroscopic features.
[57]
In the twentieth century, physicists began to apply the same concepts
to black holes. In most systems such as gases, the entropy scales with
the volume. In the 1970s, the physicist
Jacob Bekenstein suggested that the entropy of a black hole is instead proportional to the
surface area of its
event horizon, the boundary beyond which matter and radiation is lost to its gravitational attraction.
[58] When combined with ideas of the physicist
Stephen Hawking,
[59] Bekenstein's work yielded a precise formula for the entropy of a black hole. The
Bekenstein–Hawking formula expresses the entropy
S as

where
c is the
speed of light,
k is
Boltzmann's constant,
ħ is the
reduced Planck constant,
G is
Newton's constant, and
A is the surface area of the event horizon.
[60]
Like any physical system, a black hole has an entropy defined in
terms of the number of different microstates that lead to the same
macroscopic features. The Bekenstein–Hawking entropy formula gives the
expected value of the entropy of a black hole, but by the 1990s,
physicists still lacked a derivation of this formula by counting
microstates in a theory of quantum gravity. Finding such a derivation of
this formula was considered an important test of the viability of any
theory of quantum gravity such as string theory.
[61]
Derivation within string theory
In a paper from 1996,
Andrew Strominger and
Cumrun Vafa showed how to derive the Beckenstein–Hawking formula for certain black holes in string theory.
[62]
Their calculation was based on the observation that D-branes—which look
like fluctuating membranes when they are weakly interacting—become
dense, massive objects with event horizons when the interactions are
strong. In other words, a system of strongly interacting D-branes in
string theory is indistinguishable from a black hole. Strominger and
Vafa analyzed such D-brane systems and calculated the number of
different ways of placing D-branes in spacetime so that their combined
mass and charge is equal to a given mass and charge for the resulting
black hole. Their calculation reproduced the Bekenstein–Hawking formula
exactly, including the factor of
1/4.
[63]
Subsequent work by Strominger, Vafa, and others refined the original
calculations and gave the precise values of the "quantum corrections"
needed to describe very small black holes.
[64][65]
The black holes that Strominger and Vafa considered in their original
work were quite different from real astrophysical black holes. One
difference was that Strominger and Vafa considered only
extremal black holes
in order to make the calculation tractable. These are defined as black
holes with the lowest possible mass compatible with a given charge.
[66] Strominger and Vafa also restricted attention to black holes in five-dimensional spacetime with unphysical supersymmetry.
[67]
Although it was originally developed in this very particular and
physically unrealistic context in string theory, the entropy calculation
of Strominger and Vafa has led to a qualitative understanding of how
black hole entropy can be accounted for in any theory of quantum
gravity. Indeed, in 1998, Strominger argued that the original result
could be generalized to an arbitrary consistent theory of quantum
gravity without relying on strings or supersymmetry.
[68]
In collaboration with several other authors in 2010, he showed that
some results on black hole entropy could be extended to non-extremal
astrophysical black holes.
[69][70]
AdS/CFT correspondence
One approach to formulating string theory and studying its properties
is provided by the anti-de Sitter/conformal field theory (AdS/CFT)
correspondence. This is a theoretical result which implies that string
theory is in some cases equivalent to a quantum field theory. In
addition to providing insights into the mathematical structure of string
theory, the AdS/CFT correspondence has shed light on many aspects of
quantum field theory in regimes where traditional calculational
techniques are ineffective.
[6] The AdS/CFT correspondence was first proposed by
Juan Maldacena in late 1997.
[71] Important aspects of the correspondence were elaborated in articles by
Steven Gubser,
Igor Klebanov, and
Alexander Markovich Polyakov,
[72] and by Edward Witten.
[73] By 2010, Maldacena's article had over 7000 citations, becoming the most highly cited article in the field of
high energy physics.
[c]
Overview of the correspondence
In the AdS/CFT correspondence, the geometry of spacetime is described in terms of a certain
vacuum solution of
Einstein's equation called
anti-de Sitter space.
[74]
In very elementary terms, anti-de Sitter space is a mathematical model
of spacetime in which the notion of distance between points (the
metric) is different from the notion of distance in ordinary
Euclidean geometry. It is closely related to
hyperbolic space, which can be viewed as a
disk as illustrated on the left.
[75] This image shows a
tessellation
of a disk by triangles and squares. One can define the distance between
points of this disk in such a way that all the triangles and squares
are the same size and the circular outer boundary is infinitely far from
any point in the interior.
[76]
One can imagine a stack of hyperbolic disks where each disk
represents the state of the universe at a given time. The resulting
geometric object is three-dimensional anti-de Sitter space.
[75] It looks like a solid
cylinder in which any
cross section
is a copy of the hyperbolic disk. Time runs along the vertical
direction in this picture. The surface of this cylinder plays an
important role in the AdS/CFT correspondence. As with the hyperbolic
plane, anti-de Sitter space is
curved in such a way that any point in the interior is actually infinitely far from this boundary surface.
[76]
This construction describes a hypothetical universe with only two
space dimensions and one time dimension, but it can be generalized to
any number of dimensions. Indeed, hyperbolic space can have more than
two dimensions and one can "stack up" copies of hyperbolic space to get
higher-dimensional models of anti-de Sitter space.
[75]
An important feature of anti-de Sitter space is its boundary (which
looks like a cylinder in the case of three-dimensional anti-de Sitter
space). One property of this boundary is that, within a small region on
the surface around any given point, it looks just like
Minkowski space, the model of spacetime used in nongravitational physics.
[77]
One can therefore consider an auxiliary theory in which "spacetime" is
given by the boundary of anti-de Sitter space. This observation is the
starting point for AdS/CFT correspondence, which states that the
boundary of anti-de Sitter space can be regarded as the "spacetime" for a
quantum field theory. The claim is that this quantum field theory is
equivalent to a gravitational theory, such as string theory, in the bulk
anti-de Sitter space in the sense that there is a "dictionary" for
translating entities and calculations in one theory into their
counterparts in the other theory. For example, a single particle in the
gravitational theory might correspond to some collection of particles in
the boundary theory. In addition, the predictions in the two theories
are quantitatively identical so that if two particles have a 40 percent
chance of colliding in the gravitational theory, then the corresponding
collections in the boundary theory would also have a 40 percent chance
of colliding.
[78]
Applications to quantum gravity
The discovery of the AdS/CFT correspondence was a major advance in
physicists' understanding of string theory and quantum gravity. One
reason for this is that the correspondence provides a formulation of
string theory in terms of quantum field theory, which is well understood
by comparison. Another reason is that it provides a general framework
in which physicists can study and attempt to resolve the paradoxes of
black holes.
[56]
In 1975, Stephen Hawking published a calculation which suggested that
black holes are not completely black but emit a dim radiation due to
quantum effects near the
event horizon.
[59]
At first, Hawking's result posed a problem for theorists because it
suggested that black holes destroy information. More precisely,
Hawking's calculation seemed to conflict with one of the basic
postulates of quantum mechanics, which states that physical systems evolve in time according to the
Schrödinger equation. This property is usually referred to as
unitarity
of time evolution. The apparent contradiction between Hawking's
calculation and the unitarity postulate of quantum mechanics came to be
known as the
black hole information paradox.
[79]
The AdS/CFT correspondence resolves the black hole information
paradox, at least to some extent, because it shows how a black hole can
evolve in a manner consistent with quantum mechanics in some contexts.
Indeed, one can consider black holes in the context of the AdS/CFT
correspondence, and any such black hole corresponds to a configuration
of particles on the boundary of anti-de Sitter space.
[80]
These particles obey the usual rules of quantum mechanics and in
particular evolve in a unitary fashion, so the black hole must also
evolve in a unitary fashion, respecting the principles of quantum
mechanics.
[81]
In 2005, Hawking announced that the paradox had been settled in favor
of information conservation by the AdS/CFT correspondence, and he
suggested a concrete mechanism by which black holes might preserve
information.
[82]
Applications to nuclear physics

In addition to its applications to theoretical problems in quantum
gravity, the AdS/CFT correspondence has been applied to a variety of
problems in quantum field theory. One physical system that has been
studied using the AdS/CFT correspondence is the
quark–gluon plasma, an exotic
state of matter produced in
particle accelerators. This state of matter arises for brief instants when heavy
ions such as
gold or
lead nuclei are collided at high energies. Such collisions cause the
quarks that make up atomic nuclei to
deconfine at temperatures of approximately two
trillion kelvins, conditions similar to those present at around
10−11 seconds after the
Big Bang.
[83]
The physics of the quark–gluon plasma is governed by a theory called
quantum chromodynamics, but this theory is mathematically intractable in problems involving the quark–gluon plasma.
[d] In an article appearing in 2005,
Đàm Thanh Sơn
and his collaborators showed that the AdS/CFT correspondence could be
used to understand some aspects of the quark–gluon plasma by describing
it in the language of string theory.
[84]
By applying the AdS/CFT correspondence, Sơn and his collaborators were
able to describe the quark gluon plasma in terms of black holes in
five-dimensional spacetime. The calculation showed that the ratio of two
quantities associated with the quark–gluon plasma, the
shear viscosity and volume density of entropy, should be approximately equal to a certain universal
constant. In 2008, the predicted value of this ratio for the quark–gluon plasma was confirmed at the
Relativistic Heavy Ion Collider at
Brookhaven National Laboratory.
[85][86]
Applications to condensed matter physics
The AdS/CFT correspondence has also been used to study aspects of condensed matter physics. Over the decades,
experimental condensed matter physicists have discovered a number of exotic states of matter, including
superconductors and
superfluids.
These states are described using the formalism of quantum field theory,
but some phenomena are difficult to explain using standard field
theoretic techniques. Some condensed matter theorists including
Subir Sachdev
hope that the AdS/CFT correspondence will make it possible to describe
these systems in the language of string theory and learn more about
their behavior.
[85]
So far some success has been achieved in using string theory methods to describe the transition of a superfluid to an
insulator. A superfluid is a system of
electrically neutral atoms that flows without any
friction. Such systems are often produced in the laboratory using
liquid helium,
but recently experimentalists have developed new ways of producing
artificial superfluids by pouring trillions of cold atoms into a lattice
of criss-crossing
lasers.
These atoms initially behave as a superfluid, but as experimentalists
increase the intensity of the lasers, they become less mobile and then
suddenly transition to an insulating state. During the transition, the
atoms behave in an unusual way. For example, the atoms slow to a halt at
a rate that depends on the
temperature and on
Planck's constant, the fundamental parameter of quantum mechanics, which does not enter into the description of the other
phases.
This behavior has recently been understood by considering a dual
description where properties of the fluid are described in terms of a
higher dimensional black hole.
[87]
Phenomenology
In addition to being an idea of considerable theoretical interest,
string theory provides a framework for constructing models of real world
physics that combine general relativity and particle physics.
Phenomenology
is the branch of theoretical physics in which physicists construct
realistic models of nature from more abstract theoretical ideas.
String phenomenology is the part of string theory that attempts to construct realistic or semi-realistic models based on string theory.
Partly because of theoretical and mathematical difficulties and
partly because of the extremely high energies needed to test these
theories experimentally, there is so far no experimental evidence that
would unambiguously point to any of these models being a correct
fundamental description of nature. This has led some in the community to
criticize these approaches to unification and question the value of
continued research on these problems.
[12]
Particle physics
The currently accepted theory describing elementary particles and their interactions is known as the
standard model of particle physics.
This theory provides a unified description of three of the fundamental
forces of nature: electromagnetism and the strong and weak nuclear
forces. Despite its remarkable success in explaining a wide range of
physical phenomena, the standard model cannot be a complete description
of reality. This is because the standard model fails to incorporate the
force of gravity and because of problems such as the
hierarchy problem and the inability to explain the structure of fermion masses or dark matter.
String theory has been used to construct a variety of models of
particle physics going beyond the standard model. Typically, such models
are based on the idea of compactification. Starting with the ten- or
eleven-dimensional spacetime of string or M-theory, physicists postulate
a shape for the extra dimensions. By choosing this shape appropriately,
they can construct models roughly similar to the standard model of
particle physics, together with additional undiscovered particles.
[88]
One popular way of deriving realistic physics from string theory is to
start with the heterotic theory in ten dimensions and assume that the
six extra dimensions of spacetime are shaped like a six-dimensional
Calabi–Yau manifold. Such compactifications offer many ways of
extracting realistic physics from string theory. Other similar methods
can be used to construct realistic or semi-realistic models of our
four-dimensional world based on M-theory.
[89]
Cosmology

The Big Bang theory is the prevailing
cosmological
model for the universe from the earliest known periods through its
subsequent large-scale evolution. Despite its success in explaining many
observed features of the universe including galactic
redshifts, the relative abundance of light elements such as
hydrogen and
helium, and the existence of a
cosmic microwave background,
there are several questions that remain unanswered. For example, the
standard Big Bang model does not explain why the universe appears to be
same in all directions, why it appears flat on very large distance
scales, or why certain hypothesized particles such as
magnetic monopoles are not observed in experiments.
[90]
Currently, the leading candidate for a theory going beyond the Big Bang is the theory of cosmic inflation. Developed by
Alan Guth
and others in the 1980s, inflation postulates a period of extremely
rapid accelerated expansion of the universe prior to the expansion
described by the standard Big Bang theory. The theory of cosmic
inflation preserves the successes of the Big Bang while providing a
natural explanation for some of the mysterious features of the universe.
[91]
The theory has also received striking support from observations of the
cosmic microwave background, the radiation that has filled the sky since
around 380,000 years after the Big Bang.
[92]
In the theory of inflation, the rapid initial expansion of the universe is caused by a hypothetical particle called the
inflaton.
The exact properties of this particle are not fixed by the theory but
should ultimately be derived from a more fundamental theory such as
string theory.
[93]
Indeed, there have been a number of attempts to identify an inflaton
within the spectrum of particles described by string theory, and to
study inflation using string theory. While these approaches might
eventually find support in observational data such as measurements of
the cosmic microwave background, the application of string theory to
cosmology is still in its early stages.
[94]
Connections to mathematics
In addition to influencing research in
theoretical physics, string theory has stimulated a number of major developments in
pure mathematics. Like many developing ideas in theoretical physics, string theory does not at present have a
mathematically rigorous
formulation in which all of its concepts can be defined precisely. As a
result, physicists who study string theory are often guided by physical
intuition to conjecture relationships between the seemingly different
mathematical structures that are used to formalize different parts of
the theory. These conjectures are later proved by mathematicians, and in
this way, string theory serves as a source of new ideas in pure
mathematics.
[95]
Mirror symmetry

After Calabi–Yau manifolds had entered physics as a way to compactify
extra dimensions in string theory, many physicists began studying these
manifolds. In the late 1980s, several physicists noticed that given
such a compactification of string theory, it is not possible to
reconstruct uniquely a corresponding Calabi–Yau manifold.
[96]
Instead, two different versions of string theory, type IIA and type
IIB, can be compactified on completely different Calabi–Yau manifolds
giving rise to the same physics. In this situation, the manifolds are
called mirror manifolds, and the relationship between the two physical
theories is called
mirror symmetry.
[97]
Regardless of whether Calabi–Yau compactifications of string theory
provide a correct description of nature, the existence of the mirror
duality between different string theories has significant mathematical
consequences. The Calabi–Yau manifolds used in string theory are of
interest in pure mathematics, and mirror symmetry allows mathematicians
to solve problems in
enumerative geometry, a branch of mathematics concerned with counting the numbers of solutions to geometric questions.
[31][98]
Enumerative geometry studies a class of geometric objects called
algebraic varieties which are defined by the vanishing of
polynomials. For example, the
Clebsch cubic illustrated on the right is an algebraic variety defined using a certain polynomial of
degree three in four variables. A celebrated result of nineteenth-century mathematicians
Arthur Cayley and
George Salmon states that there are exactly 27 straight lines that lie entirely on such a surface.
[99]
Generalizing this problem, one can ask how many lines can be drawn on
a quintic Calabi–Yau manifold, such as the one illustrated above, which
is defined by a polynomial of degree five. This problem was solved by
the nineteenth-century German mathematician
Hermann Schubert,
who found that there are exactly 2,875 such lines. In 1986, geometer
Sheldon Katz proved that the number of curves, such as circles, that are
defined by polynomials of degree two and lie entirely in the quintic is
609,250.
[100]
By the year 1991, most of the classical problems of enumerative
geometry had been solved and interest in enumerative geometry had begun
to diminish.
[101] The field was reinvigorated in May 1991 when physicists
Philip Candelas,
Xenia de la Ossa, Paul Green, and Linda Parks showed that mirror
symmetry could be used to translate difficult mathematical questions
about one Calabi–Yau manifold into easier questions about its mirror.
[102]
In particular, they used mirror symmetry to show that a six-dimensional
Calabi–Yau manifold can contain exactly 317,206,375 curves of degree
three.
[101]
In addition to counting degree-three curves, Candelas and his
collaborators obtained a number of more general results for counting
rational curves which went far beyond the results obtained by
mathematicians.
[103]
Originally, these results of Candelas were justified on physical
grounds. However, mathematicians generally prefer rigorous proofs that
do not require an appeal to physical intuition. Inspired by physicists'
work on mirror symmetry, mathematicians have therefore constructed their
own arguments proving the enumerative predictions of mirror symmetry.
[e]
Today mirror symmetry is an active area of research in mathematics, and
mathematicians are working to develop a more complete mathematical
understanding of mirror symmetry based on physicists' intuition.
[104] Major approaches to mirror symmetry include the
homological mirror symmetry program of
Maxim Kontsevich[32] and the
SYZ conjecture of Andrew Strominger, Shing-Tung Yau, and
Eric Zaslow.
[105]
Monstrous moonshine

An equilateral triangle can be rotated through 120°, 240°, or 360°, or
reflected in any of the three lines pictured without changing its shape.
Group theory is the branch of mathematics that studies the concept of
symmetry.
For example, one can consider a geometric shape such as an equilateral
triangle. There are various operations that one can perform on this
triangle without changing its shape. One can rotate it through 120°,
240°, or 360°, or one can reflect in any of the lines labeled
S0,
S1, or
S2 in the picture. Each of these operations is called a
symmetry, and the collection of these symmetries satisfies certain technical properties making it into what mathematicians call a
group. In this particular example, the group is known as the
dihedral group of
order
6 because it has six elements. A general group may describe finitely
many or infinitely many symmetries; if there are only finitely many
symmetries, it is called a
finite group.
[106]
Mathematicians often strive for a
classification
(or list) of all mathematical objects of a given type. It is generally
believed that finite groups are too diverse to admit a useful
classification. A more modest but still challenging problem is to
classify all finite
simple groups. These are finite groups which
may be used as building blocks for constructing arbitrary finite groups
in the same way that
prime numbers can be used to construct arbitrary
whole numbers by taking products.
[f] One of the major achievements of contemporary group theory is the
classification of finite simple groups, a mathematical theorem which provides a list of all possible finite simple groups.
[107]
This classification theorem identifies several infinite families of
groups as well as 26 additional groups which do not fit into any family.
The latter groups are called the "sporadic" groups, and each one owes
its existence to a remarkable combination of circumstances. The largest
sporadic group, the so-called
monster group, has over
1053 elements, more than a thousand times the number of atoms in the Earth.
[108]
A seemingly unrelated construction is the
j-function of
number theory. This object belongs to a special class of functions called
modular functions, whose graphs form a certain kind of repeating pattern.
[109]
Although this function appears in a branch of mathematics which seems
very different from the theory of finite groups, the two subjects turn
out to be intimately related. In the late 1970s, mathematicians
John McKay and
John Thompson noticed that certain numbers arising in the analysis of the monster group (namely, the dimensions of its
irreducible representations) are related to numbers that appear in a formula for the
j-function (namely, the coefficients of its
Fourier series).
[110] This relationship was further developed by
John Horton Conway and
Simon Norton[111] who called it
monstrous moonshine because it seemed so far fetched.
[112]
In 1992,
Richard Borcherds
constructed a bridge between the theory of modular functions and finite
groups and, in the process, explained the observations of McKay and
Thompson.
[113][114] Borcherds' work used ideas from string theory in an essential way, extending earlier results of
Igor Frenkel,
James Lepowsky, and
Arne Meurman, who had realized the monster group as the symmetries of a particular
[which?] version of string theory.
[115] In 1998, Borcherds was awarded the
Fields medal for his work.
[116]
Since the 1990s, the connection between string theory and moonshine has led to further results in mathematics and physics.
[108] In 2010, physicists Tohru Eguchi,
Hirosi Ooguri, and
Yuji Tachikawa discovered connections between a different sporadic group, the
Mathieu group M24, and a certain version
[which?] of string theory.
[117] Miranda Cheng, John Duncan, and
Jeffrey A. Harvey proposed a generalization of this moonshine phenomenon called
umbral moonshine,
[118] and their conjecture was proved mathematically by Duncan, Michael Griffin, and
Ken Ono.
[119]
Witten has also speculated that the version of string theory appearing
in monstrous moonshine might be related to a certain simplified model of
gravity in three spacetime dimensions.
[120]
History
Early results
Some of the structures reintroduced by string theory arose for the
first time much earlier as part of the program of classical unification
started by
Albert Einstein. The first person to add a
fifth dimension to a theory of gravity was
Gunnar Nordström
in 1914, who noted that gravity in five dimensions describes both
gravity and electromagnetism in four. Nordström attempted to unify
electromagnetism with
his theory of gravitation, which was however superseded by Einstein's general relativity in 1919. Thereafter, German mathematician
Theodor Kaluza combined the fifth dimension with
general relativity, and only Kaluza is usually credited with the idea. In 1926, the Swedish physicist
Oskar Klein gave
a physical interpretation of the unobservable extra dimension—it is wrapped into a small circle. Einstein introduced a
non-symmetric metric tensor,
while much later Brans and Dicke added a scalar component to gravity.
These ideas would be revived within string theory, where they are
demanded by consistency conditions.
String theory was originally developed during the late 1960s and early 1970s as a never completely successful theory of
hadrons, the
subatomic particles like the
proton and
neutron that feel the
strong interaction. In the 1960s,
Geoffrey Chew and
Steven Frautschi discovered that the
mesons make families called
Regge trajectories with masses related to spins in a way that was later understood by
Yoichiro Nambu,
Holger Bech Nielsen and
Leonard Susskind
to be the relationship expected from rotating strings. Chew advocated
making a theory for the interactions of these trajectories that did not
presume that they were composed of any fundamental particles, but would
construct their interactions from
self-consistency conditions on the
S-matrix. The
S-matrix approach was started by
Werner Heisenberg
in the 1940s as a way of constructing a theory that did not rely on the
local notions of space and time, which Heisenberg believed break down
at the nuclear scale. While the scale was off by many orders of
magnitude, the approach he advocated was ideally suited for a theory of
quantum gravity.
Working with experimental data, R. Dolen, D. Horn and C. Schmid
developed some sum rules for hadron exchange. When a particle and
antiparticle
scatter, virtual particles can be exchanged in two qualitatively
different ways. In the s-channel, the two particles annihilate to make
temporary intermediate states that fall apart into the final state
particles. In the t-channel, the particles exchange intermediate states
by emission and absorption. In field theory, the two contributions add
together, one giving a continuous background contribution, the other
giving peaks at certain energies. In the data, it was clear that the
peaks were stealing from the background—the authors interpreted this as
saying that the t-channel contribution was dual to the s-channel one,
meaning both described the whole amplitude and included the other.
The result was widely advertised by
Murray Gell-Mann, leading
Gabriele Veneziano to construct a
scattering amplitude
that had the property of Dolen–Horn–Schmid duality, later renamed
world-sheet duality. The amplitude needed poles where the particles
appear, on straight line trajectories, and there is a special
mathematical function whose poles are evenly spaced on half the real
line—the
gamma function—
which was widely used in Regge theory. By manipulating combinations of
gamma functions, Veneziano was able to find a consistent scattering
amplitude with poles on straight lines, with mostly positive residues,
which obeyed duality and had the appropriate Regge scaling at high
energy. The amplitude could fit near-beam scattering data as well as
other Regge type fits, and had a suggestive integral representation that
could be used for generalization.
Over the next years, hundreds of physicists worked to complete the
bootstrap program
for this model, with many surprises. Veneziano himself discovered that
for the scattering amplitude to describe the scattering of a particle
that appears in the theory, an obvious self-consistency condition, the
lightest particle must be a
tachyon.
Miguel Virasoro and Joel Shapiro found a different amplitude now understood to be that of closed strings, while
Ziro Koba and
Holger Nielsen generalized Veneziano's integral representation to multiparticle scattering. Veneziano and
Sergio Fubini introduced an operator formalism for computing the scattering amplitudes that was a forerunner of
world-sheet conformal theory, while Virasoro understood how to remove the poles with wrong-sign residues using a constraint on the states.
Claud Lovelace calculated a loop amplitude, and noted that there is an inconsistency unless the dimension of the theory is 26.
Charles Thorn,
Peter Goddard and
Richard Brower went on to prove that there are no wrong-sign propagating states in dimensions less than or equal to 26.
In 1969–70,
Yoichiro Nambu,
Holger Bech Nielsen, and
Leonard Susskind
recognized that the theory could be given a description in space and
time in terms of strings. The scattering amplitudes were derived
systematically from the action principle by
Peter Goddard,
Jeffrey Goldstone,
Claudio Rebbi, and
Charles Thorn,
giving a space-time picture to the vertex operators introduced by
Veneziano and Fubini and a geometrical interpretation to the
Virasoro conditions.
In 1971,
Pierre Ramond added fermions to the model, which led him to formulate a two-dimensional supersymmetry to cancel the wrong-sign states.
John Schwarz and
André Neveu added another sector to the fermi theory a short time later. In the fermion theories, the critical dimension was 10.
Stanley Mandelstam
formulated a world sheet conformal theory for both the bose and fermi
case, giving a two-dimensional field theoretic path-integral to generate
the operator formalism.
Michio Kaku and
Keiji Kikkawa gave a different formulation of the bosonic string, as a
string field theory, with infinitely many particle types and with fields taking values not on points, but on loops and curves.
In 1974,
Tamiaki Yoneya discovered that all the known string theories included a massless spin-two particle that obeyed the correct
Ward identities to be a graviton. John Schwarz and
Joel Scherk
came to the same conclusion and made the bold leap to suggest that
string theory was a theory of gravity, not a theory of hadrons. They
reintroduced
Kaluza–Klein theory as a way of making sense of the extra dimensions. At the same time,
quantum chromodynamics
was recognized as the correct theory of hadrons, shifting the attention
of physicists and apparently leaving the bootstrap program in the
dustbin of history.
String theory eventually made it out of the dustbin, but for the
following decade all work on the theory was completely ignored. Still,
the theory continued to develop at a steady pace thanks to the work of a
handful of devotees.
Ferdinando Gliozzi, Joel Scherk, and
David Olive
realized in 1977 that the original Ramond and Neveu Schwarz-strings
were separately inconsistent and needed to be combined. The resulting
theory did not have a tachyon, and was proven to have space-time
supersymmetry by John Schwarz and
Michael Green in 1984. The same year,
Alexander Polyakov gave the theory a modern path integral formulation, and went on to develop conformal field theory extensively. In 1979,
Daniel Friedan showed that the equations of motions of string theory, which are generalizations of the
Einstein equations of
general relativity, emerge from the
renormalization group
equations for the two-dimensional field theory. Schwarz and Green
discovered T-duality, and constructed two superstring theories—IIA and
IIB related by T-duality, and type I theories with open strings. The
consistency conditions had been so strong, that the entire theory was
nearly uniquely determined, with only a few discrete choices.
First superstring revolution
In the early 1980s,
Edward Witten discovered that most theories of quantum gravity could not accommodate
chiral fermions like the neutrino. This led him, in collaboration with
Luis Álvarez-Gaumé, to study violations of the conservation laws in gravity theories with
anomalies,
concluding that type I string theories were inconsistent. Green and
Schwarz discovered a contribution to the anomaly that Witten and
Alvarez-Gaumé had missed, which restricted the gauge group of the type I
string theory to be SO(32). In coming to understand this calculation,
Edward Witten became convinced that string theory was truly a consistent
theory of gravity, and he became a high-profile advocate. Following
Witten's lead, between 1984 and 1986, hundreds of physicists started to
work in this field, and this is sometimes called the
first superstring revolution.
During this period,
David Gross,
Jeffrey Harvey,
Emil Martinec, and
Ryan Rohm discovered
heterotic strings. The gauge group of these closed strings was two copies of
E8, and either copy could easily and naturally include the standard model.
Philip Candelas,
Gary Horowitz,
Andrew Strominger
and Edward Witten found that the Calabi–Yau manifolds are the
compactifications that preserve a realistic amount of supersymmetry,
while
Lance Dixon and others worked out the physical properties of
orbifolds, distinctive geometrical singularities allowed in string theory.
Cumrun Vafa generalized T-duality from circles to arbitrary manifolds, creating the mathematical field of
mirror symmetry.
Daniel Friedan,
Emil Martinec and
Stephen Shenker further developed the covariant quantization of the superstring using conformal field theory techniques.
David Gross and
Vipul Periwal discovered that string perturbation theory was divergent.
Stephen Shenker showed it diverged much faster than in field theory suggesting that new non-perturbative objects were missing.
In the 1990s,
Joseph Polchinski discovered that the theory requires higher-dimensional objects, called
D-branes
and identified these with the black-hole solutions of supergravity.
These were understood to be the new objects suggested by the
perturbative divergences, and they opened up a new field with rich
mathematical structure. It quickly became clear that D-branes and other
p-branes, not just strings, formed the matter content of the string
theories, and the physical interpretation of the strings and branes was
revealed—they are a type of black hole.
Leonard Susskind had incorporated the
holographic principle of
Gerardus 't Hooft
into string theory, identifying the long highly excited string states
with ordinary thermal black hole states. As suggested by 't Hooft, the
fluctuations of the black hole horizon, the world-sheet or world-volume
theory, describes not only the degrees of freedom of the black hole, but
all nearby objects too.
Second superstring revolution
In 1995, at the annual conference of string theorists at the University of Southern California (USC),
Edward Witten
gave a speech on string theory that in essence united the five string
theories that existed at the time, and giving birth to a new
11-dimensional theory called
M-theory. M-theory was also foreshadowed in the work of
Paul Townsend at approximately the same time. The flurry of activity that began at this time is sometimes called the
second superstring revolution.
[34]
During this period,
Tom Banks,
Willy Fischler,
Stephen Shenker and
Leonard Susskind formulated matrix theory, a full holographic description of M-theory using IIA D0 branes.
[51] This was the first definition of string theory that was fully non-perturbative and a concrete mathematical realization of the
holographic principle. It is an example of a gauge-gravity duality and is now understood to be a special case of the
AdS/CFT correspondence.
Andrew Strominger and
Cumrun Vafa
calculated the entropy of certain configurations of D-branes and found
agreement with the semi-classical answer for extreme charged black
holes.
[62] Petr Hořava
and Witten found the eleven-dimensional formulation of the heterotic
string theories, showing that orbifolds solve the chirality problem.
Witten noted that the effective description of the physics of D-branes
at low energies is by a supersymmetric gauge theory, and found
geometrical interpretations of mathematical structures in gauge theory
that he and
Nathan Seiberg had earlier discovered in terms of the location of the branes.
In 1997,
Juan Maldacena
noted that the low energy excitations of a theory near a black hole
consist of objects close to the horizon, which for extreme charged black
holes looks like an
anti-de Sitter space.
[71]
He noted that in this limit the gauge theory describes the string
excitations near the branes. So he hypothesized that string theory on a
near-horizon extreme-charged black-hole geometry, an anti-de Sitter
space times a sphere with flux, is equally well described by the
low-energy limiting
gauge theory, the
N = 4 supersymmetric Yang–Mills theory. This hypothesis, which is called the
AdS/CFT correspondence, was further developed by
Steven Gubser,
Igor Klebanov and
Alexander Polyakov,
[72] and by
Edward Witten,
[73] and it is now well-accepted. It is a concrete realization of the
holographic principle, which has far-reaching implications for
black holes,
locality and
information in physics, as well as the nature of the gravitational interaction.
[56] Through this relationship, string theory has been shown to be related to gauge theories like
quantum chromodynamics and this has led to more quantitative understanding of the behavior of
hadrons, bringing string theory back to its roots.
[84]
Criticism
Number of solutions
To construct models of particle physics based on string theory,
physicists typically begin by specifying a shape for the extra
dimensions of spacetime. Each of these different shapes corresponds to a
different possible universe, or "vacuum state", with a different
collection of particles and forces. String theory as it is currently
understood has an enormous number of vacuum states, typically estimated
to be around
10500, and these might be sufficiently diverse to accommodate almost any phenomena that might be observed at low energies.
[121]
Many critics of string theory have expressed concerns about the large
number of possible universes described by string theory. In his book
Not Even Wrong,
Peter Woit, a lecturer in the mathematics department at
Columbia University,
has argued that the large number of different physical scenarios
renders string theory vacuous as a framework for constructing models of
particle physics. According to Woit,
The possible existence of, say, 10500
consistent different vacuum states for superstring theory probably
destroys the hope of using the theory to predict anything. If one picks
among this large set just those states whose properties agree with
present experimental observations, it is likely there still will be such
a large number of these that one can get just about whatever value one
wants for the results of any new observation.[122]
Some physicists believe this large number of solutions is actually a
virtue because it may allow a natural anthropic explanation of the
observed values of
physical constants, in particular the small value of the cosmological constant.
[122] The
anthropic principle
is the idea that some of the numbers appearing in the laws of physics
are not fixed by any fundamental principle but must be compatible with
the evolution of intelligent life. In 1987,
Steven Weinberg published an article in which he argued that the cosmological constant could not have been too large, or else
galaxies and intelligent life would not have been able to develop.
[123]
Weinberg suggested that there might be a huge number of possible
consistent universes, each with a different value of the cosmological
constant, and observations indicate a small value of the cosmological
constant only because humans happen to live in a universe that has
allowed intelligent life, and hence observers, to exist.
[124]
String theorist Leonard Susskind has argued that string theory
provides a natural anthropic explanation of the small value of the
cosmological constant.
[125] According to Susskind, the different vacuum states of string theory might be realized as different universes within a larger
multiverse.
The fact that the observed universe has a small cosmological constant
is just a tautological consequence of the fact that a small value is
required for life to exist.
[126] Many prominent theorists and critics have disagreed with Susskind's conclusions.
[127]
According to Woit, "in this case [anthropic reasoning] is nothing more
than an excuse for failure. Speculative scientific ideas fail not just
when they make incorrect predictions, but also when they turn out to be
vacuous and incapable of predicting anything."
[128]
Background independence
One of the fundamental properties of Einstein's general theory of relativity is that it is
background independent, meaning that the formulation of the theory does not in any way privilege a particular spacetime geometry.
[129]
One of the main criticisms of string theory from early on is that it
is not manifestly background independent. In string theory, one must
typically specify a fixed reference geometry for spacetime, and all
other possible geometries are described as perturbations of this fixed
one. In his book
The Trouble With Physics, physicist
Lee Smolin of the
Perimeter Institute for Theoretical Physics
claims that this is the principal weakness of string theory as a theory
of quantum gravity, saying that string theory has failed to incorporate
this important insight from general relativity.
[130]
Others have disagreed with Smolin's characterization of string
theory. In a review of Smolin's book, string theorist Joseph Polchinski
writes
[Smolin] is mistaking an aspect of the mathematical language being
used for one of the physics being described. New physical theories are
often discovered using a mathematical language that is not the most
suitable for them… In string theory it has always been clear that the
physics is background-independent even if the language being used is
not, and the search for more suitable language continues. Indeed, as
Smolin belatedly notes, [AdS/CFT] provides a solution to this problem,
one that is unexpected and powerful.[131]
Polchinski notes that an important open problem in quantum gravity is
to develop holographic descriptions of gravity which do not require the
gravitational field to be asymptotically anti-de Sitter.
[131]
Smolin has responded by saying that the AdS/CFT correspondence, as it
is currently understood, may not be strong enough to resolve all
concerns about background independence.
[g]
Sociological issues
Since the superstring revolutions of the 1980s and 1990s, string
theory has become the dominant paradigm of high energy theoretical
physics.
[132]
Some string theorists have expressed the view that there does not exist
an equally successful alternative theory addressing the deep questions
of fundamental physics. In an interview from 1987,
Nobel laureate David Gross made the following controversial comments about the reasons for the popularity of string theory:
The most important [reason] is that there are no other good ideas
around. That's what gets most people into it. When people started to get
interested in string theory they didn't know anything about it. In
fact, the first reaction of most people is that the theory is extremely
ugly and unpleasant, at least that was the case a few years ago when the
understanding of string theory was much less developed. It was
difficult for people to learn about it and to be turned on. So I think
the real reason why people have got attracted by it is because there is
no other game in town. All other approaches of constructing grand
unified theories, which were more conservative to begin with, and only
gradually became more and more radical, have failed, and this game
hasn't failed yet.[133]
Several other high-profile theorists and commentators have expressed
similar views, suggesting that there are no viable alternatives to
string theory.
[134]
Many critics of string theory have commented on this state of
affairs. In his book criticizing string theory, Peter Woit views the
status of string theory research as unhealthy and detrimental to the
future of fundamental physics. He argues that the extreme popularity of
string theory among theoretical physicists is partly a consequence of
the financial structure of academia and the fierce competition for
scarce resources.
[135] In his book
The Road to Reality, mathematical physicist
Roger Penrose
expresses similar views, stating "The often frantic competitiveness
that this ease of communication engenders leads to 'bandwagon' effects,
where researchers fear to be left behind if they do not join in."
[136]
Penrose also claims that the technical difficulty of modern physics
forces young scientists to rely on the preferences of established
researchers, rather than forging new paths of their own.
[137] Lee Smolin expresses a slightly different position in his critique,
claiming that string theory grew out of a tradition of particle physics
which discourages speculation about the foundations of physics, while
his preferred approach,
loop quantum gravity, encourages more radical thinking. According to Smolin,
String theory is a powerful, well-motivated idea and deserves much of
the work that has been devoted to it. If it has so far failed, the
principal reason is that its intrinsic flaws are closely tied to its
strengths—and, of course, the story is unfinished, since string theory
may well turn out to be part of the truth. The real question is not why
we have expended so much energy on string theory but why we haven't
expended nearly enough on alternative approaches.[138]
Smolin goes on to offer a number of prescriptions for how scientists
might encourage a greater diversity of approaches to quantum gravity
research.
[139]