MAGA Miracle: Op-ed by conservative economist in WaPo supporting EPA transparency rulemaking is EPA media release

Original post:  https://junkscience.com/2018/05/maga-miracle-op-ed-by-conservative-economist-in-wapo-supporting-epa-transparency-rulemaking-is-epa-media-release/#more-93749

The combination of the Washington Post printing an op-ed by a conservative economist supporting the Scott Pruitt-led EPA’s science transparency initiative, which then becomes an EPA media release… well, that just doesn’t happen every day!




Many Mocked This Scott Pruitt Proposal.  They Should Have Read It First.
The Washington Post
By Robert Hahn
May 10, 2018

https://www.washingtonpost.com/opinions/many-mocked-this-scott-pruitt-proposal-they-should-have-read-it-first/2018/05/10/31baba9a-53c2-11e8-abd8-265bd07a9859_story.html?noredirect=on&utm_term=.f7bcbc0a1887

Robert Hahn is a visiting professor at Oxford University’s Smith School of Enterprise and the Environment and a non-resident senior fellow at the Brookings Institution. He recently served as a commissioner on the U.S. Commission on Evidence-Based Policymaking.

When Environmental Protection Agency Administrator Scott Pruitt proposed a rule last month to improve transparency in science used to make policy decisions, he was roundly criticized by interest groups and academics. Several researchers asserted that the policy would be used to undermine a litany of existing environmental protections. Former Obama administration EPA officials co-wrote a New York Times op-ed in which they said the proposal “would undermine the nation’s scientific credibility.” The Economist derided the policy as “swamp science.”

But there is a lot to cheer about in the rule that opponents have missed. A careful reading suggests it could promote precisely the kind of evidence-based policy most scientists and the public should support.

Critics typically argue that the proposed regulation would suppress research that contains confidential medical records and therefore scientists could not share underlying data publicly for privacy reasons. Such restrictions, these critics say, would have excluded landmark research, such as Harvard University’s “Six Cities” study, which suggested that reducing fine particles in the air would dramatically improve human health and helped lead to more stringent regulation of fine particles in the United States.
…
But it appears that few defenders or opponents of the proposal have actually read the proposed EPA regulation, which is only seven pages long. Both sides distort the regulatory text.

Here’s what the rule would actually do. First, it would require the EPA to identify studies that are used in making regulatory decisions. Second, it would encourage studies to be made publicly available “to the extent practicable.” Third, it would define “publicly available” by listing examples of information that could be used for validation, such as underlying data, models, computer code and protocols. Fourth, the proposal recognizes not all data can be openly accessible in the public domain and that restricted access to some data may be necessary. Fifth, it would direct the EPA to work with third parties, including universities and private firms, to make information available to the extent reasonable. Sixth, it would encourage the use of efforts to de-identify data sets to create public-use data files that would simultaneously help protect privacy and promote transparency. Seventh, the proposal outlines an exemption process when compliance is “impracticable.” Finally, it would direct the EPA to clearly state and document assumptions made in regulatory analyses.

Here’s what the EPA’s rule wouldn’t do: nullify existing environmental regulations, disregard existing research, violate confidentiality protections, jeopardize privacy or undermine the peer-review process.

The costs of compliance with EPA regulations are substantial. A draft report from the White House Office of Management and Budget suggests that significant EPA regulations imposed costs ranging from $54 billion to $65 billion over the past decade. These rules also realize substantial public-health and environmental benefits estimated to range from $196 billion to $706 billion over the decade.

Given the stakes for both the cost of compliance with EPA regulations and the real risks that pollution poses to public health and the environment, this rule should be read closely by critics and supporters for what it actually says. Just as transparency in science and evidence are essential, so, too, are intellectual honesty and accurate policy communication.

Taking steps to increase access to data, with strong privacy protections, is how society will continue to make scientific and economic progress and ensure that evidence in rule-making is sound. The EPA’s proposed rule follows principles laid out in 2017 by the bipartisan Commission on Evidence-Based Policymaking — humility, transparency, privacy, capacity and rigor — and moves us toward providing greater access to scientific data while protecting individual privacy.

Instead of throwing stones, the scientific community should come together to offer practical suggestions to make the rule better. For example, the rule should recognize the incentives for scientists to produce new research. Scientists need to have time to produce and take credit for their research findings. Thus, there will inevitably be a trade-off between the production of new insights and the sharing of data with others, including regulators.

Done right, this could improve government policy not only in the United States but also around the world.

It’s still hard to tell how this rule will affect EPA decisions, but one thing is clear: The rule will make the evidence by which we make policy decisions more transparent. The policy might not be perfect, but its benefits will likely far outweigh its costs.

Maximum parsimony (phylogenetics)

From Wikipedia, the free encyclopedia

In phylogenetics, maximum parsimony is an optimality criterion under which the phylogenetic tree that minimizes the total number of character-state changes is to be preferred. Under the maximum-parsimony criterion, the optimal tree will minimize the amount of homoplasy (i.e., convergent evolution, parallel evolution, and evolutionary reversals). In other words, under this criterion, the shortest possible tree that explains the data is considered best. The principle is akin to Occam's razor, which states that—all else being equal—the simplest hypothesis that explains the data should be selected. Some of the basic ideas behind maximum parsimony were presented by James S. Farris ^[1] in 1970 and Walter M. Fitch in 1971.^[2]

Maximum parsimony is an intuitive and simple criterion, and it is popular for this reason. However, although it is easy to score a phylogenetic tree (by counting the number of character-state changes), there is no algorithm to quickly generate the most-parsimonious tree. Instead, the most-parsimonious tree must be found in "tree space" (i.e., amongst all possible trees). For a small number of taxa (i.e., fewer than nine) it is possible to do an exhaustive search, in which every possible tree is scored, and the best one is selected. For nine to twenty taxa, it will generally be preferable to use branch-and-bound, which is also guaranteed to return the best tree. For greater numbers of taxa, a heuristic search must be performed.

Because the most-parsimonious tree is always the shortest possible tree, this means that—in comparison to the "true" tree that actually describes the evolutionary history of the organisms under study—the "best" tree according to the maximum-parsimony criterion will often underestimate the actual evolutionary change that has occurred. In addition, maximum parsimony is not statistically consistent. That is, it is not guaranteed to produce the true tree with high probability, given sufficient data. As demonstrated in 1978 by Joe Felsenstein,^[3] maximum parsimony can be inconsistent under certain conditions, such as long-branch attraction. Of course, any phylogenetic algorithm could also be statistically inconsistent if the model it employs to estimate the preferred tree does not accurately match the way that evolution occurred in that clade. This is unknowable. Therefore, while statistical consistency is an interesting theoretical property, it lies outside the realm of testability, and is irrelevant to empirical phylogenetic studies.^[4].

Alternate characterization and rationale

The maximization of parsimony (preferring the simpler of two otherwise equally adequate theorizations) has proven useful in many fields. Occam's razor, a principle of theoretical parsimony suggested by William of Ockham in the 1320s, asserted that it is vain to give an explanation which involves more assumptions than necessary.

Alternatively, phylogenetic parsimony can be characterized as favoring the trees that maximize explanatory power by minimizing the number of observed similarities that cannot be explained by inheritance and common descent.^[5][6] Minimization of required evolutionary change on the one hand and maximization of observed similarities that can be explained as homology on the other may result in different preferred trees when some observed features are not applicable in some groups that are included in the tree, and the latter can be seen as the more general approach.^[7][8]

While evolution is not an inherently parsimonious process, centuries of scientific experience lend support to the aforementioned principle of parsimony (Occam's razor). Namely, the supposition of a simpler, more parsimonious chain of events is preferable to the supposition of a more complicated, less parsimonious chain of events. Hence, parsimony (sensu lato) is typically sought in constructing phylogenetic trees, and in scientific explanation generally.^[9]

In detail

Parsimony is part of a class of character-based tree estimation methods which use a matrix of discrete phylogenetic characters to infer one or more optimal phylogenetic trees for a set of taxa, commonly a set of species or reproductively isolated populations of a single species. These methods operate by evaluating candidate phylogenetic trees according to an explicit optimality criterion; the tree with the most favorable score is taken as the best estimate of the phylogenetic relationships of the included taxa. Maximum parsimony is used with most kinds of phylogenetic data; until recently, it was the only widely used character-based tree estimation method used for morphological data.

Estimating phylogenies is not a trivial problem. A huge number of possible phylogenetic trees exist for any reasonably sized set of taxa; for example, a mere ten species gives over two million possible unrooted trees. These possibilities must be searched to find a tree that best fits the data according to the optimality criterion. However, the data themselves do not lead to a simple, arithmetic solution to the problem. Ideally, we would expect the distribution of whatever evolutionary characters (such as phenotypic traits or alleles) to directly follow the branching pattern of evolution. Thus we could say that if two organisms possess a shared character, they should be more closely related to each other than to a third organism that lacks this character (provided that character was not present in the last common ancestor of all three, in which case it would be a symplesiomorphy). We would predict that bats and monkeys are more closely related to each other than either is to an elephant, because male bats and monkeys possess external testicles, which elephants lack. However, we cannot say that bats and monkeys are more closely related to one another than they are to whales, though the two have external testicles absent in whales, because we believe that the males in the last common ancestral species of the three had external testicles.

However, the phenomena of convergent evolution, parallel evolution, and evolutionary reversals (collectively termed homoplasy) add an unpleasant wrinkle to the problem of estimating phylogeny. For a number of reasons, two organisms can possess a trait not present in their last common ancestor: If we naively took the presence of this trait as evidence of a relationship, we would reconstruct an incorrect tree. Real phylogenetic data include substantial homoplasy, with different parts of the data suggesting sometimes very different relationships. Methods used to estimate phylogenetic trees are explicitly intended to resolve the conflict within the data by picking the phylogenetic tree that is the best fit to all the data overall, accepting that some data simply will not fit. It is often mistakenly believed that parsimony assumes that convergence is rare; in fact, even convergently derived characters have some value in maximum-parsimony-based phylogenetic analyses, and the prevalence of convergence does not systematically affect the outcome of parsimony-based methods.^[10]

Data that do not fit a tree perfectly are not simply "noise", they can contain relevant phylogenetic signal in some parts of a tree, even if they conflict with the tree overall. In the whale example given above, the lack of external testicles in whales is homoplastic: It reflects a return to the condition present in ancient ancestors of mammals, whose testicles were internal. This similarity between whales and ancient mammal ancestors is in conflict with the tree we accept, since it implies that the mammals with external testicles should form a group excluding whales. However, among the whales, the reversal to internal testicles actually correctly associates the various types of whales (including dolphins and porpoises) into the group Cetacea. Still, the determination of the best-fitting tree—and thus which data do not fit the tree—is a complex process. Maximum parsimony is one method developed to do this.

Character data

The input data used in a maximum parsimony analysis is in the form of "characters" for a range of taxa. There is no generally agreed-upon definition of a phylogenetic character, but operationally a character can be thought of as an attribute, an axis along which taxa are observed to vary. These attributes can be physical (morphological), molecular, genetic, physiological, or behavioral. The only widespread agreement on characters seems to be that variation used for character analysis should reflect heritable variation. Whether it must be directly heritable, or whether indirect inheritance (e.g., learned behaviors) is acceptable, is not entirely resolved.

Each character is divided into discrete character states, into which the variations observed are classified. Character states are often formulated as descriptors, describing the condition of the character substrate. For example, the character "eye color" might have the states "blue" and "brown." Characters can have two or more states (they can have only one, but these characters lend nothing to a maximum parsimony analysis, and are often excluded).

Coding characters for phylogenetic analysis is not an exact science, and there are numerous complicating issues. Typically, taxa are scored with the same state if they are more similar to one another in that particular attribute than each is to taxa scored with a different state. This is not straightforward when character states are not clearly delineated or when they fail to capture all of the possible variation in a character. How would one score the previously mentioned character for a taxon (or individual) with hazel eyes? Or green? As noted above, character coding is generally based on similarity: Hazel and green eyes might be lumped with blue because they are more similar to that color (being light), and the character could be then recoded as "eye color: light; dark." Alternatively, there can be multi-state characters, such as "eye color: brown; hazel, blue; green."

Ambiguities in character state delineation and scoring can be a major source of confusion, dispute, and error in phylogenetic analysis using character data. Note that, in the above example, "eyes: present; absent" is also a possible character, which creates issues because "eye color" is not applicable if eyes are not present. For such situations, a "?" ("unknown") is scored, although sometimes "X" or "-" (the latter usually in sequence data) are used to distinguish cases where a character cannot be scored from a case where the state is simply unknown. Current implementations of maximum parsimony generally treat unknown values in the same manner: the reasons the data are unknown have no particular effect on analysis. Effectively, the program treats a ? as if it held the state that would involve the fewest extra steps in the tree (see below), although this is not an explicit step in the algorithm.

Genetic data are particularly amenable to character-based phylogenetic methods such as maximum parsimony because protein and nucleotide sequences are naturally discrete: A particular position in a nucleotide sequence can be either adenine, cytosine, guanine, or thymine / uracil, or a sequence gap; a position (residue) in a protein sequence will be one of the basic amino acids or a sequence gap. Thus, character scoring is rarely ambiguous, except in cases where sequencing methods fail to produce a definitive assignment for a particular sequence position. Sequence gaps are sometimes treated as characters, although there is no consensus on how they should be coded.

Characters can be treated as unordered or ordered. For a binary (two-state) character, this makes little difference. For a multi-state character, unordered characters can be thought of as having an equal "cost" (in terms of number of "evolutionary events") to change from any one state to any other; complementarily, they do not require passing through intermediate states. Ordered characters have a particular sequence in which the states must occur through evolution, such that going between some states requires passing through an intermediate. This can be thought of complementarily as having different costs to pass between different pairs of states. In the eye-color example above, it is possible to leave it unordered, which imposes the same evolutionary "cost" to go from brown-blue, green-blue, green-hazel, etc. Alternatively, it could be ordered brown-hazel-green-blue; this would normally imply that it would cost two evolutionary events to go from brown-green, three from brown-blue, but only one from brown-hazel. This can also be thought of as requiring eyes to evolve through a "hazel stage" to get from brown to green, and a "green stage" to get from hazel to blue, etc.

There is a lively debate on the utility and appropriateness of character ordering, but no consensus. Some authorities order characters when there is a clear logical, ontogenetic, or evolutionary transition among the states (for example, "legs: short; medium; long"). Some accept only some of these criteria. Some run an unordered analysis, and order characters that show a clear order of transition in the resulting tree (which practice might be accused of circular reasoning). Some authorities refuse to order characters at all, suggesting that it biases an analysis to require evolutionary transitions to follow a particular path.

It is also possible to apply differential weighting to individual characters. This is usually done relative to a "cost" of 1. Thus, some characters might be seen as more likely to reflect the true evolutionary relationships among taxa, and thus they might be weighted at a value 2 or more; changes in these characters would then count as two evolutionary "steps" rather than one when calculating tree scores (see below). There has been much discussion in the past about character weighting. Most authorities now weight all characters equally, although exceptions are common. For example, allele frequency data is sometimes pooled in bins and scored as an ordered character. In these cases, the character itself is often downweighted so that small changes in allele frequencies count less than major changes in other characters. Also, the third codon position in a coding nucleotide sequence is particularly labile, and is sometimes downweighted, or given a weight of 0, on the assumption that it is more likely to exhibit homoplasy. In some cases, repeated analyses are run, with characters reweighted in inverse proportion to the degree of homoplasy discovered in the previous analysis (termed successive weighting); this is another technique that might be considered circular reasoning.

Character state changes can also be weighted individually. This is often done for nucleotide sequence data; it has been empirically determined that certain base changes (A-C, A-T, G-C, G-T, and the reverse changes) occur much less often than others. These changes are therefore often weighted more. As shown above in the discussion of character ordering, ordered characters can be thought of as a form of character state weighting.

Some systematists prefer to exclude characters known to be, or suspected to be, highly homoplastic or that have a large number of unknown entries ("?"). As noted below, theoretical and simulation work has demonstrated that this is likely to sacrifice accuracy rather than improve it. This is also the case with characters that are variable in the terminal taxa: theoretical, congruence, and simulation studies have all demonstrated that such polymorphic characters contain significant phylogenetic information.^{[citation needed]}

Taxon sampling

The time required for a parsimony analysis (or any phylogenetic analysis) is proportional to the number of taxa (and characters) included in the analysis. Also, because more taxa require more branches to be estimated, more uncertainty may be expected in large analyses. Because data collection costs in time and money often scale directly with the number of taxa included, most analyses include only a fraction of the taxa that could have been sampled. Indeed, some authors have contended that four taxa (the minimum required to produce a meaningful unrooted tree) are all that is necessary for accurate phylogenetic analysis, and that more characters are more valuable than more taxa in phylogenetics. This has led to a raging controversy about taxon sampling.

Empirical, theoretical, and simulation studies have led to a number of dramatic demonstrations of the importance of adequate taxon sampling. Most of these can be summarized by a simple observation: a phylogenetic data matrix has dimensions of characters times taxa. Doubling the number of taxa doubles the amount of information in a matrix just as surely as doubling the number of characters. Each taxon represents a new sample for every character, but, more importantly, it (usually) represents a new combination of character states. These character states can not only determine where that taxon is placed on the tree, they can inform the entire analysis, possibly causing different relationships among the remaining taxa to be favored by changing estimates of the pattern of character changes.

The most disturbing weakness of parsimony analysis, that of long-branch attraction (see below) is particularly pronounced with poor taxon sampling, especially in the four-taxon case. This is a well-understood case in which additional character sampling may not improve the quality of the estimate. As taxa are added, they often break up long branches (especially in the case of fossils), effectively improving the estimation of character state changes along them. Because of the richness of information added by taxon sampling, it is even possible to produce highly accurate estimates of phylogenies with hundreds of taxa using only a few thousand characters.^{[citation needed]}

Although many studies have been performed, there is still much work to be done on taxon sampling strategies. Because of advances in computer performance, and the reduced cost and increased automation of molecular sequencing, sample sizes overall are on the rise, and studies addressing the relationships of hundreds of taxa (or other terminal entities, such as genes) are becoming common. Of course, this is not to say that adding characters is not also useful; the number of characters is increasing as well.

Some systematists prefer to exclude taxa based on the number of unknown character entries ("?") they exhibit, or because they tend to "jump around" the tree in analyses (i.e., they are "wildcards"). As noted below, theoretical and simulation work has demonstrated that this is likely to sacrifice accuracy rather than improve it. Although these taxa may generate more most-parsimonious trees (see below), methods such as agreement subtrees and reduced consensus can still extract information on the relationships of interest.

It has been observed that inclusion of more taxa tends to lower overall support values (bootstrap percentages or decay indices, see below). The cause of this is clear: as additional taxa are added to a tree, they subdivide the branches to which they attach, and thus dilute the information that supports that branch. While support for individual branches is reduced, support for the overall relationships is actually increased. Consider analysis that produces the following tree: (fish, (lizard, (whale, (cat, monkey)))). Adding a rat and a walrus will probably reduce the support for the (whale, (cat, monkey)) clade, because the rat and the walrus may fall within this clade, or outside of the clade, and since these five animals are all relatively closely related, there should be more uncertainty about their relationships. Within error, it may be impossible to determine any of these animals' relationships relative to one another. However, the rat and the walrus will probably add character data that cements the grouping any two of these mammals exclusive of the fish or the lizard; where the initial analysis might have been misled, say, by the presence of fins in the fish and the whale, the presence of the walrus, with blubber and fins like a whale but whiskers like a cat and a rat, firmly ties the whale to the mammals.

To cope with this problem, agreement subtrees, reduced consensus, and double-decay analysis seek to identify supported relationships (in the form of "n-taxon statements," such as the four-taxon statement "(fish, (lizard, (cat, whale)))") rather than whole trees. If the goal of an analysis is a resolved tree, as is the case for comparative phylogenetics, these methods cannot solve the problem. However, if the tree estimate is so poorly supported, the results of any analysis derived from the tree will probably be too suspect to use anyway.

Analysis

A maximum parsimony analysis runs in a very straightforward fashion. Trees are scored according to the degree to which they imply a parsimonious distribution of the character data. The most parsimonious tree for the dataset represents the preferred hypothesis of relationships among the taxa in the analysis.

Trees are scored (evaluated) by using a simple algorithm to determine how many "steps" (evolutionary transitions) are required to explain the distribution of each character. A step is, in essence, a change from one character state to another, although with ordered characters some transitions require more than one step. Contrary to popular belief, the algorithm does not explicitly assign particular character states to nodes (branch junctions) on a tree: the least number of steps can involve multiple, equally costly assignments and distributions of evolutionary transitions. What is optimized is the total number of changes.

There are many more possible phylogenetic trees than can be searched exhaustively for more than eight taxa or so. A number of algorithms are therefore used to search among the possible trees. Many of these involve taking an initial tree (usually the favored tree from the last iteration of the algorithm), and perturbing it to see if the change produces a higher score.

The trees resulting from parsimony search are unrooted: They show all the possible relationships of the included taxa, but they lack any statement on relative times of divergence. A particular branch is chosen to root the tree by the user. This branch is then taken to be outside all the other branches of the tree, which together form a monophyletic group. This imparts a sense of relative time to the tree. Incorrect choice of a root can result in incorrect relationships on the tree, even if the tree is itself correct in its unrooted form.

Parsimony analysis often returns a number of equally most-parsimonious trees (MPTs). A large number of MPTs is often seen as an analytical failure, and is widely believed to be related to the number of missing entries ("?") in the dataset, characters showing too much homoplasy, or the presence of topologically labile "wildcard" taxa (which may have many missing entries). Numerous methods have been proposed to reduce the number of MPTs, including removing characters or taxa with large amounts of missing data before analysis, removing or downweighting highly homoplastic characters (successive weighting) or removing wildcard taxa (the phylogenetic trunk method) a posteriori and then reanalyzing the data.

Numerous theoretical and simulation studies have demonstrated that highly homoplastic characters, characters and taxa with abundant missing data, and "wildcard" taxa contribute to the analysis. Although excluding characters or taxa may appear to improve resolution, the resulting tree is based on less data, and is therefore a less reliable estimate of the phylogeny (unless the characters or taxa are non informative, see safe taxonomic reduction). Today's general consensus is that having multiple MPTs is a valid analytical result; it simply indicates that there is insufficient data to resolve the tree completely. In many cases, there is substantial common structure in the MPTs, and differences are slight and involve uncertainty in the placement of a few taxa. There are a number of methods for summarizing the relationships within this set, including consensus trees, which show common relationships among all the taxa, and pruned agreement subtrees, which show common structure by temporarily pruning "wildcard" taxa from every tree until they all agree. Reduced consensus takes this one step further, by showing all subtrees (and therefore all relationships) supported by the input trees.

Even if multiple MPTs are returned, parsimony analysis still basically produces a point-estimate, lacking confidence intervals of any sort. This has often been levelled as a criticism, since there is certainly error in estimating the most-parsimonious tree, and the method does not inherently include any means of establishing how sensitive its conclusions are to this error. Several methods have been used to assess support.

Jackknifing and bootstrapping, well-known statistical resampling procedures, have been employed with parsimony analysis. The jackknife, which involves resampling without replacement ("leave-one-out") can be employed on characters or taxa; interpretation may become complicated in the latter case, because the variable of interest is the tree, and comparison of trees with different taxa is not straightforward. The bootstrap, resampling with replacement (sample x items randomly out of a sample of size x, but items can be picked multiple times), is only used on characters, because adding duplicate taxa does not change the result of a parsimony analysis. The bootstrap is much more commonly employed in phylogenetics (as elsewhere); both methods involve an arbitrary but large number of repeated iterations involving perturbation of the original data followed by analysis. The resulting MPTs from each analysis are pooled, and the results are usually presented on a 50% Majority Rule Consensus tree, with individual branches (or nodes) labelled with the percentage of bootstrap MPTs in which they appear. This "bootstrap percentage" (which is not a P-value, as is sometimes claimed) is used as a measure of support. Technically, it is supposed to be a measure of repeatability, the probability that that branch (node, clade) would be recovered if the taxa were sampled again. Experimental tests with viral phylogenies suggest that the bootstrap percentage is not a good estimator of repeatability for phylogenetics, but it is a reasonable estimator of accuracy.^{[citation needed]} In fact, it has been shown that the bootstrap percentage, as an estimator of accuracy, is biased, and that this bias results on average in an underestimate of confidence (such that as little as 70% support might really indicate up to 95% confidence). However, the direction of bias cannot be ascertained in individual cases, so assuming that high values bootstrap support indicate even higher confidence is unwarranted.

Another means of assessing support is Bremer support^[11][12], or the decay index which is a parameter of a given data set, rather than an estimate based on pseudoreplicated subsamples, as are the bootstrap and jackknife procedures described above. Bremer support (also known as branch support) is simply the difference in number of steps between the score of the MPT(s), and the score of the most parsimonious tree that does not contain a particular clade (node, branch). It can be thought of as the number of steps you have to add to lose that clade; implicitly, it is meant to suggest how great the error in the estimate of the score of the MPT must be for the clade to no longer be supported by the analysis, although this is not necessarily what it does. Branch support values are often fairly low for modestly-sized data sets (one or two steps being typical), but they often appear to be proportional to bootstrap percentages. As data matrices become larger, branch support values often continue to increase as bootstrap values plateau at 100%. Thus, for large data matrices, branch support values may provide a more informative means to compare support for strongly-supported branches^[13]. However, interpretation of decay values is not straightforward, and they seem to be preferred by authors with philosophical objections to the bootstrap (although many morphological systematists, especially paleontologists, report both). Double-decay analysis is a decay counterpart to reduced consensus that evaluates the decay index for all possible subtree relationships (n-taxon statements) within a tree.

Problems with maximum parsimony phylogenetic inference

An example of long branch attraction. If branches A & C have a high number of substitutions in the "true tree" (assumed, never actually known except in simulations), then parsimony might interpret parallel changes as synapomorphies and group A and C together. 

Maximum parsimony is an epistemologically straightforward approach that makes few mechanistic assumptions, and is popular for this reason. However, it may not be statistically consistent under certain circumstances. Consistency, here meaning the monotonic convergence on the correct answer with the addition of more data, is a desirable property of statistical methods. As demonstrated in 1978 by Joe Felsenstein,^[3] maximum parsimony can be inconsistent under certain conditions. The category of situations in which this is known to occur is called long branch attraction, and occurs, for example, where there are long branches (a high level of substitutions) for two characters (A & C), but short branches for another two (B & D). A and B diverged from a common ancestor, as did C and D.

Assume for simplicity that we are considering a single binary character (it can either be + or -). Because the distance from B to D is small, in the vast majority of all cases, B and D will be the same. Here, we will assume that they are both + (+ and - are assigned arbitrarily and swapping them is only a matter of definition). If this is the case, there are four remaining possibilities. A and C can both be +, in which case all taxa are the same and all the trees have the same length. A can be + and C can be -, in which case only one character is different, and we cannot learn anything, as all trees have the same length. Similarly, A can be - and C can be +. The only remaining possibility is that A and C are both -. In this case, however, the evidence suggests that A and C group together, and B and D together. As a consequence, if the "true tree" is a tree of this type, the more data we collect (i.e. the more characters we study), the more the evidence will support the wrong tree. Of course, except in mathematical simulations, we never know what the "true tree" is. Thus, unless we are able to devise a model that is guaranteed to accurately recover the "true tree," any other optimality criterion or weighting scheme could also, in principle, be statistically inconsistent. The bottom line is, that while statistical inconsistency is an interesting theoretical issue, it is empirically a purely metaphysical concern, outside the realm of empirical testing. Any method could be inconsistent, and there is no way to know for certain whether it is, or not. It is for this reason that many systematists characterize their phylogenetic results as hypotheses of relationship.

Another complication with maximum parsimony, and other optimaltiy-criterion based phylogenetic methods, is that finding the shortest tree is an NP-hard problem.^[14] The only currently available, efficient way of obtaining a solution, given an arbitrarily large set of taxa, is by using heuristic methods which do not guarantee that the shortest tree will be recovered. These methods employ hill-climbing algorithms to progressively approach the best tree. However, it has been shown that there can be "tree islands" of suboptimal solutions, and the analysis can become trapped in these local optima. Thus, complex, flexible heuristics are required to ensure that tree space has been adequately explored. Several heuristics are available, including nearest neighbor interchange (NNI), tree bisection reconnection (TBR), and the parsimony ratchet.

Criticism

It has been asserted that a major problem, especially for paleontology, is that maximum parsimony assumes that the only way two species can share the same nucleotide at the same position is if they are genetically related^{[citation needed]}. This asserts that phylogenetic applications of parsimony assume that all similarity is homologous (other interpretations, such as the assertion that two organisms might not be related at all, are nonsensical). This is emphatically not the case: as with any form of character-based phylogeny estimation, parsimony is used to test the homologous nature of similarities by finding the phylogenetic tree which best accounts for all of the similarities.

It is often stated that parsimony is not relevant to phylogenetic inference because "evolution is not parsimonious."^{[citation needed]} In most cases, there is no explicit alternative proposed; if no alternative is available, any statistical method is preferable to none at all. Additionally, it is not clear what would be meant if the statement "evolution is parsimonious" were in fact true. This could be taken to mean that more character changes may have occurred historically than are predicted using the parsimony criterion. Because parsimony phylogeny estimation reconstructs the minimum number of changes necessary to explain a tree, this is quite possible. However, it has been shown through simulation studies, testing with known in vitro viral phylogenies, and congruence with other methods, that the accuracy of parsimony is in most cases not compromised by this. Parsimony analysis uses the number of character changes on trees to choose the best tree, but it does not require that exactly that many changes, and no more, produced the tree. As long as the changes that have not been accounted for are randomly distributed over the tree (a reasonable null expectation), the result should not be biased. In practice, the technique is robust: maximum parsimony exhibits minimal bias as a result of choosing the tree with the fewest changes.

An analogy can be drawn with choosing among contractors based on their initial (nonbinding) estimate of the cost of a job. The actual finished cost is very likely to be higher than the estimate. Despite this, choosing the contractor who furnished the lowest estimate should theoretically result in the lowest final project cost. This is because, in the absence of other data, we would assume that all of the relevant contractors have the same risk of cost overruns. In practice, of course, unscrupulous business practices may bias this result; in phylogenetics, too, some particular phylogenetic problems (for example, long branch attraction, described above) may potentially bias results. In both cases, however, there is no way to tell if the result is going to be biased, or the degree to which it will be biased, based on the estimate itself. With parsimony too, there is no way to tell that the data are positively misleading, without comparison to other evidence.

Parsimony is often characterized as implicitly adopting the position that evolutionary change is rare, or that homoplasy (convergence and reversal) is minimal in evolution. This is not entirely true: parsimony minimizes the number of convergences and reversals that are assumed by the preferred tree, but this may result in a relatively large number of such homoplastic events. It would be more appropriate to say that parsimony assumes only the minimum amount of change implied by the data. As above, this does not require that these were the only changes that occurred; it simply does not infer changes for which there is no evidence. The shorthand for describing this is that "parsimony minimizes assumed homoplasies, it does not assume that homoplasy is minimal."

Parsimony is also sometimes associated with the notion that "the simplest possible explanation is the best," a generalisation of Occam's Razor. Parsimony does prefer the solution that requires the least number of unsubstantiated assumptions and unsupportable conclusions, the solution that goes the least theoretical distance beyond the data. This is a very common approach to science, especially when dealing with systems that are so complex as to defy simple models. Parsimony does not by any means necessarily produce a "simple" assumption. Indeed, as a general rule, most character datasets are so "noisy" that no truly "simple" solution is possible.

Alternatives

There are several other methods for inferring phylogenies based on discrete character data, including maximum likelihood and Bayesian inference. Each offers potential advantages and disadvantages. In practice, these methods tend to favor trees that are very similar to the most parsimonious tree(s) for the same dataset^[15]; however, they allow for complex modelling of evolutionary processes, and as classes of methods are statistically consistent and are not susceptible to long-branch attraction. Note, however, that the performance of likelihood and Bayesian methods are dependent on the quality of the particular model of evolution employed; an incorrect model can produce a biased result - just like parsimony. In addition, they are still quite computationally slow relative to parsimony methods, sometimes requiring weeks to run large datasets. Most of these methods have particularly avid proponents and detractors; parsimony especially has been advocated as philosophically superior (most notably by ardent cladists).^{[citation needed]} One area where parsimony still holds much sway is in the analysis of morphological data, because—until recently—stochastic models of character change were not available for non-molecular data, and they are still not widely implemented. Parsimony has also recently been shown to be more likely to recover the true tree in the face of profound changes in evolutionary ("model") parameters (e.g., the rate of evolutionary change) within a tree (Kolaczkowski & Thornton 2004).

Distance matrices can also be used to generate phylogenetic trees. Non-parametric distance methods were originally applied to phenetic data using a matrix of pairwise distances and reconciled to produce a tree. The distance matrix can come from a number of different sources, including immunological distance, morphometric analysis, and genetic distances. For phylogenetic character data, raw distance values can be calculated by simply counting the number of pairwise differences in character states (Manhattan distance) or by applying a model of evolution. Notably, distance methods also allow use of data that may not be easily converted to character data, such as DNA-DNA hybridization assays. Today, distance-based methods are often frowned upon because phylogenetically-informative data can be lost when converting characters to distances. There are a number of distance-matrix methods and optimality criteria, of which the minimum evolution criterion is most closely related to maximum parsimony.

Minimum evolution

The minimum-evolution tree-optimality criterion is similar to the maximum-parsimony criterion in that the tree that has the shortest total branch lengths is said to be optimal. The difference between these two criteria is that minimum evolution is calculated from a distance matrix, whereas maximum parsimony is calculated directly using the character matrix. Like the maximum-parsimony tree, the minimum-evolution tree must be sought in "tree space", typically using a heuristic search method. The neighbor-joining algorithm is very fast and often produces a tree that is quite similar to the minimum-evolution tree.

Language family

From Wikipedia, the free encyclopedia

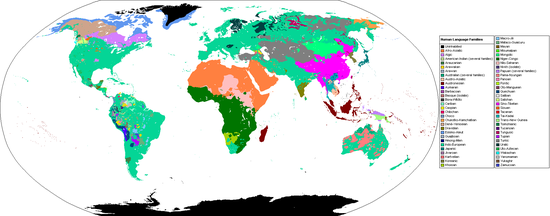
Contemporary distribution (2005 map) of the world's major language families (in some cases geographic groups of families).

A language family is a group of languages related through descent from a common ancestral language or parental language, called the proto-language of that family. The term "family" reflects the tree model of language origination in historical linguistics, which makes use of a metaphor comparing languages to people in a biological family tree, or in a subsequent modification, to species in a phylogenetic tree of evolutionary taxonomy. Linguists therefore describe the daughter languages within a language family as being genetically related.^[1]

A "living language" is simply one that is used as the primary form of communication of a group of people. There are also many dead and extinct languages, as well as some that are still insufficiently studied to be classified, or are even unknown outside their respective speech communities.

Membership of languages in a language family is established by comparative linguistics. Sister languages are said to have a "genetic" or "genealogical" relationship. The latter term is older.^[2] Speakers of a language family belong to a common speech community. The divergence of a proto-language into daughter languages typically occurs through geographical separation, with the original speech community gradually evolving into distinct linguistic units. Individuals belonging to other speech communities may also adopt languages from a different language family through the language shift process.^[3]

Genealogically related languages present shared retentions; that is, features of the proto-language (or reflexes of such features) that cannot be explained by chance or borrowing (convergence). Membership in a branch or group within a language family is established by shared innovations; that is, common features of those languages that are not found in the common ancestor of the entire family. For example, Germanic languages are "Germanic" in that they share vocabulary and grammatical features that are not believed to have been present in the Proto-Indo-European language. These features are believed to be innovations that took place in Proto-Germanic, a descendant of Proto-Indo-European that was the source of all Germanic languages.

Structure of a family

Language families can be divided into smaller phylogenetic units, conventionally referred to as branches of the family because the history of a language family is often represented as a tree diagram. A family is a monophyletic unit; all its members derive from a common ancestor, and all attested descendants of that ancestor are included in the family. (Thus, the term family is analogous to the biological term clade.)

Some taxonomists restrict the term family to a certain level, but there is little consensus in how to do so. Those who affix such labels also subdivide branches into groups, and groups into complexes. A top-level (i.e., the largest) family is often called a phylum or stock. The closer the branches are to each other, the closer the languages will be related. This means if a branch off of a proto-language is 4 branches down and there is also a sister language to that fourth branch, than each of the two sister languages are more closely related to each other than to that common ancestral proto-language.

The term macrofamily or superfamily is sometimes applied to proposed groupings of language families whose status as phylogenetic units is generally considered to be unsubstantiated by accepted historical linguistic methods. For example, the Celtic, Germanic, Slavic, Romance, and Indo-Iranian language families are branches of a larger Indo-European language family. There is a remarkably similar pattern shown by the linguistic tree and the genetic tree of human ancestry^[4] that was verified statistically.^[5] Languages interpreted in terms of the putative phylogenetic tree of human languages are transmitted to a great extent vertically (by ancestry) as opposed to horizontally (by spatial diffusion).^[6]

Dialect continua

Some closely knit language families, and many branches within larger families, take the form of dialect continua in which there are no clear-cut borders that make it possible to unequivocally identify, define, or count individual languages within the family. However, when the differences between the speech of different regions at the extremes of the continuum are so great that there is no mutual intelligibility between them, as occurs in Arabic, the continuum cannot meaningfully be seen as a single language.

A speech variety may also be considered either a language or a dialect depending on social or political considerations. Thus, different sources, especially over time, can give wildly different numbers of languages within a certain family. Classifications of the Japonic family, for example, range from one language (a language isolate with dialects) to nearly twenty—until the classification of Ryukyuan as separate languages within a Japonic language family rather than dialects of Japanese, the Japanese language itself was considered a language isolate and therefore the only language in its family.

Isolates

Most of the world's languages are known to be related to others. Those that have no known relatives (or for which family relationships are only tentatively proposed) are called language isolates, essentially language families consisting of a single language. An example is Basque. In general, it is assumed that language isolates have relatives or had relatives at some point in their history but at a time depth too great for linguistic comparison to recover them.

A language isolated in its own branch within a family, such as Armenian within Indo-European, is often also called an isolate, but the meaning of the word "isolate" in such cases is usually clarified with a modifier. For instance, Armenian may be referred to as an "Indo-European isolate". By contrast, so far as is known, the Basque language is an absolute isolate: it has not been shown to be related to any other language despite numerous attempts. Another well-known isolate is Mapudungun, the Mapuche language from the Araucanían language family in Chile. A language may be said to be an isolate currently but not historically if related but now extinct relatives are attested. The Aquitanian language, spoken in Roman times, may have been an ancestor of Basque, but it could also have been a sister language to the ancestor of Basque. In the latter case, Basque and Aquitanian would form a small family together. (Ancestors are not considered to be distinct members of a family.)

Proto-languages

A proto-language can be thought of as a mother language (not to be confused with a mother tongue, which is one that a specific person has been exposed to from birth^[7]), being the root which all languages in the family stem from. The common ancestor of a language family is seldom known directly since most languages have a relatively short recorded history. However, it is possible to recover many features of a proto-language by applying the comparative method, a reconstructive procedure worked out by 19th century linguist August Schleicher. This can demonstrate the validity of many of the proposed families in the list of language families. For example, the reconstructible common ancestor of the Indo-European language family is called Proto-Indo-European. Proto-Indo-European is not attested by written records and so is conjectured to have been spoken before the invention of writing.

Sometimes, however, a proto-language can be identified with a historically known language. For instance, dialects of Old Norse are the proto-language of Norwegian, Swedish, Danish, Faroese and Icelandic. Likewise, the Appendix Probi depicts Proto-Romance, a language almost unattested because of the prestige of Classical Latin, a highly stylised literary register not representative of the speech of ordinary people.

Although many languages are related through a proto-language, this does not mean that speakers of each language will necessarily understand each other. There are cases in which speakers of one language are able to understand and successfully communicate with their sister languages. But there are also cases where this is very one-sided, meaning that only one communicator is able to understand a language while the other cannot. An example of this would be how many Spanish speakers can understand Italian; however, Italians are unable to comprehend what Spanish speakers are saying. Both of these languages share a proto-language, but only bits are understood.

Other classifications of languages

Sprachbund

Shared innovations, acquired by borrowing or other means, are not considered genetic and have no bearing with the language family concept. It has been asserted, for example, that many of the more striking features shared by Italic languages (Latin, Oscan, Umbrian, etc.) might well be "areal features". However, very similar-looking alterations in the systems of long vowels in the West Germanic languages greatly postdate any possible notion of a proto-language innovation (and cannot readily be regarded as "areal", either, since English and continental West Germanic were not a linguistic area). In a similar vein, there are many similar unique innovations in Germanic, Baltic and Slavic that are far more likely to be areal features than traceable to a common proto-language. But legitimate uncertainty about whether shared innovations are areal features, coincidence, or inheritance from a common ancestor, leads to disagreement over the proper subdivisions of any large language family.

A sprachbund is a geographic area having several languages that feature common linguistic structures. The similarities between those languages are caused by language contact, not by chance or common origin, and are not recognized as criteria that define a language family. An example of a sprachbund would be the Indian subcontinent.

Contact languages

The concept of language families is based on the historical observation that languages develop dialects, which over time may diverge into distinct languages. However, linguistic ancestry is less clear-cut than familiar biological ancestry, in which species do not crossbreed. It is more like the evolution of microbes, with extensive lateral gene transfer: Quite distantly related languages may affect each other through language contact, which in extreme cases may lead to languages with no single ancestor, whether they be creoles or mixed languages. In addition, a number of sign languages have developed in isolation and appear to have no relatives at all. Nonetheless, such cases are relatively rare and most well-attested languages can be unambiguously classified as belonging to one language family or another, even if this family's relation to other families is not known.

Cladistics

From Wikipedia, the free encyclopedia

Cladistics (from Greek κλάδος, klados, i.e., "branch")^[1] is an approach to biological classification in which organisms are categorized in groups ("clades") based on the most recent common ancestor. Hypothesized relationships are typically based on shared derived characteristics (synapomorphies) that can be traced to the most recent common ancestor and are not present in more distant groups and ancestors. A key feature of a clade is that all descendants stay in their overarching ancestral clade. Radiation results in the generation of new subclades by bifurcation.^[2][3][4][5]

The techniques and nomenclature of cladistics have been applied to other disciplines. (See phylogenetic nomenclature.)

History

Willi Hennig 1972

Peter Chalmers Mitchell in 1920

 

Robert John Tillyard

The original methods used in cladistic analysis and the school of taxonomy derived from the work of the German entomologist Willi Hennig, who referred to it as phylogenetic systematics (also the title of his 1966 book); the terms "cladistics" and "clade" were popularized by other researchers. Cladistics in the original sense refers to a particular set of methods used in phylogenetic analysis, although it is now sometimes used to refer to the whole field.^[6]

What is now called the cladistic method appeared as early as 1901 with a work by Peter Chalmers Mitchell for birds^[7][8] and subsequently by Robert John Tillyard (for insects) in 1921,^[9] and W. Zimmermann (for plants) in 1943.^[10] The term "clade" was introduced in 1958 by Julian Huxley after having been coined by Lucien Cuénot in 1940,^[11] "cladogenesis" in 1958,^[12] "cladistic" by Cain and Harrison in 1960,^[13] "cladist" (for an adherent of Hennig's school) by Mayr in 1965,^[14] and "cladistics" in 1966.^[12] Hennig referred to his own approach as "phylogenetic systematics". From the time of his original formulation until the end of the 1970s, cladistics competed as an analytical and philosophical approach to phylogenetic inference with phenetics and so-called evolutionary taxonomy. Phenetics was championed at this time by the numerical taxonomists Peter Sneath and Robert Sokal and the evolutionary taxonomist Ernst Mayr.

Originally conceived, if only in essence, by Willi Hennig in a book published in 1950, cladistics did not flourish until its translation into English in 1966 (Lewin 1997). Today, cladistics is the most popular method for constructing phylogenies from morphological and molecular data. Unlike phenetics, cladistics is specifically aimed at reconstructing evolutionary histories.

In the 1990s, the development of effective polymerase chain reaction techniques allowed the application of cladistic methods to biochemical and molecular genetic traits of organisms, as well as to anatomical ones, vastly expanding the amount of data available for phylogenetics. At the same time, cladistics rapidly became the dominant set of methods of phylogenetics in evolutionary biology, because computers made it possible to process large quantities of data about organisms and their characteristics.

The way for computational phylogenetics was paved by phenetics,^[15] a set of methods commonly used from the 1950s to 1980s and to some degree later. Phenetics did not try to reconstruct phylogenetic trees; rather, it tried to build dendrograms from similarity data; its algorithms required less computer power than phylogenetic ones.

Methodology

The cladistic method interprets each character state transformation implied by the distribution of shared character states among taxa (or other terminals) as a potential piece of evidence for grouping. The outcome of a cladistic analysis is a cladogram – a tree-shaped diagram (dendrogram)^[16] that is interpreted to represent the best hypothesis of phylogenetic relationships. Although traditionally such cladograms were generated largely on the basis of morphological characters and originally calculated by hand, genetic sequencing data and computational phylogenetics are now commonly used in phylogenetic analyses, and the parsimony criterion has been abandoned by many phylogeneticists in favor of more "sophisticated" but less parsimonious evolutionary models of character state transformation. Cladists contend that these models are unjustified.^[why?]

Every cladogram is based on a particular dataset analyzed with a particular method. Datasets are tables consisting of molecular, morphological, ethological^[17] and/or other characters and a list of operational taxonomic units (OTUs), which may be genes, individuals, populations, species, or larger taxa that are presumed to be monophyletic and therefore to form, all together, one large clade; phylogenetic analysis infers the branching pattern within that clade. Different datasets and different methods, not to mention violations of the mentioned assumptions, often result in different cladograms. Only scientific investigation can show which is more likely to be correct.

Until recently, for example, cladograms like the following have generally been accepted as accurate representations of the ancestral relations among turtles, lizards, crocodilians, and birds:^[18]

▼	Testudines   turtles Diapsida   ♦ Lepidosauria   lizards Archosauria Crocodylomorpha   crocodilians Dinosauria birds

If this phylogenetic hypothesis is correct, then the last common ancestor of turtles and birds, at the branch near the ▼ lived earlier than the last common ancestor of lizards and birds, near the ♦. Most molecular evidence, however, produces cladograms more like this:^[19]

Diapsida   ♦	Lepidosauria   lizards Archosauromorpha▼ Testudines   turtles Archosauria   Crocodylomorpha   crocodilians Dinosauria birds

If this is accurate, then the last common ancestor of turtles and birds lived later than the last common ancestor of lizards and birds. Since the cladograms provide competing accounts of real events, at most one of them is correct.

Cladogram of the primates, showing a monophyletic taxon (a clade: the simians or Anthropoidea, in yellow), a paraphyletic taxon (the prosimians, in blue, including the red patch), and a polyphyletic taxon (the nocturnal primates – the lorises and the tarsiers – in red)

The cladogram to the right represents the current universally accepted hypothesis that all primates, including strepsirrhines like the lemurs and lorises, had a common ancestor all of whose descendants were primates, and so form a clade; the name Primates is therefore recognized for this clade. Within the primates, all anthropoids (monkeys, apes and humans) are hypothesized to have had a common ancestor all of whose descendants were anthropoids, so they form the clade called Anthropoidea. The "prosimians", on the other hand, form a paraphyletic taxon. The name Prosimii is not used in phylogenetic nomenclature, which names only clades; the "prosimians" are instead divided between the clades Strepsirhini and Haplorhini, where the latter contains Tarsiiformes and Anthropoidea.

Terminology for character states

The following terms, coined by Hennig, are used to identify shared or distinct character states among groups:^[20][21][22]

• A plesiomorphy ("close form") or ancestral state is a character state that a taxon has retained from its ancestors. When two or more taxa that are not nested within each other share a plesiomorphy, it is a symplesiomorphy (from syn-, "together"). Symplesiomorphies do not mean that the taxa that exhibit that character state are necessarily closely related. For example, Reptilia is traditionally characterized by (among other things) being cold-blooded (i.e., not maintaining a constant high body temperature), whereas birds are warm-blooded. Since cold-bloodedness is a plesiomorphy, inherited from the common ancestor of traditional reptiles and birds, and thus a symplesiomorphy of turtles, snakes and crocodiles (among others), it does not mean that turtles, snakes and crocodiles form a clade that excludes the birds.
• An apomorphy ("separate form") or derived state is an innovation. It can thus be used to diagnose a clade – or even to help define a clade name in phylogenetic nomenclature. Features that are derived in individual taxa (a single species or a group that is represented by a single terminal in a given phylogenetic analysis) are called autapomorphies (from auto-, "self"). Autapomorphies express nothing about relationships among groups; clades are identified (or defined) by synapomorphies (from syn-, "together"). For example, the possession of digits that are homologous with those of Homo sapiens is a synapomorphy within the vertebrates. The tetrapods can be singled out as consisting of the first vertebrate with such digits homologous to those of Homo sapiens together with all descendants of this vertebrate (an apomorphy-based phylogenetic definition).^[23] Importantly, snakes and other tetrapods that do not have digits are nonetheless tetrapods: other characters, such as amniotic eggs and diapsid skulls, indicate that they descended from ancestors that possessed digits which are homologous with ours.
• A character state is homoplastic or "an instance of homoplasy" if it is shared by two or more organisms but is absent from their common ancestor or from a later ancestor in the lineage leading to one of the organisms. It is therefore inferred to have evolved by convergence or reversal. Both mammals and birds are able to maintain a high constant body temperature (i.e., they are warm-blooded). However, the accepted cladogram explaining their significant features indicates that their common ancestor is in a group lacking this character state, so the state must have evolved independently in the two clades. Warm-bloodedness is separately a synapomorphy of mammals (or a larger clade) and of birds (or a larger clade), but it is not a synapomorphy of any group including both these clades. Hennig's Auxiliary Principle ^[24] states that shared character states should be considered evidence of grouping unless they are contradicted by the weight of other evidence; thus, homoplasy of some feature among members of a group may only be inferred after a phylogenetic hypothesis for that group has been established.

The terms plesiomorphy and apomorphy are relative; their application depends on the position of a group within a tree. For example, when trying to decide whether the tetrapods form a clade, an important question is whether having four limbs is a synapomorphy of the earliest taxa to be included within Tetrapoda: did all the earliest members of the Tetrapoda inherit four limbs from a common ancestor, whereas all other vertebrates did not, or at least not homologously? By contrast, for a group within the tetrapods, such as birds, having four limbs is a plesiomorphy. Using these two terms allows a greater precision in the discussion of homology, in particular allowing clear expression of the hierarchical relationships among different homologous features.

It can be difficult to decide whether a character state is in fact the same and thus can be classified as a synapomorphy, which may identify a monophyletic group, or whether it only appears to be the same and is thus a homoplasy, which cannot identify such a group. There is a danger of circular reasoning: assumptions about the shape of a phylogenetic tree are used to justify decisions about character states, which are then used as evidence for the shape of the tree.^[25] Phylogenetics uses various forms of parsimony to decide such questions; the conclusions reached often depend on the dataset and the methods. Such is the nature of empirical science, and for this reason, most cladists refer to their cladograms as hypotheses of relationship. Cladograms that are supported by a large number and variety of different kinds of characters are viewed as more robust than those based on more limited evidence.

Terminology for taxa

Mono-, para- and polyphyletic taxa can be understood based on the shape of the tree (as done above), as well as based on their character states.^[21][22][26] These are compared in the table below.

Term	Node-based definition	Character-based definition
Monophyly	A clade, a monophyletic taxon, is a taxon that includes all descendants of an inferred ancestor.	A clade is characterized by one or more apomorphies: derived character states present in the first member of the taxon, inherited by its descendants (unless secondarily lost), and not inherited by any other taxa.
Paraphyly	A paraphyletic assemblage is one that is constructed by taking a clade and removing one or more smaller clades.[27] (Removing one clade produces a singly paraphyletic assemblage, removing two produces a doubly paraphylectic assemblage, and so on.)[28]	A paraphyletic assemblage is characterized by one or more plesiomorphies: character states inherited from ancestors but not present in all of their descendants. As a consequence, a paraphyletic assemblage is truncated, in that it excludes one or more clades from an otherwise monophyletic taxon. An alternative name is evolutionary grade, referring to an ancestral character state within the group. While paraphyletic assemblages are popular among paleontologists and evolutionary taxonomists, cladists do not recognize paraphyletic assemblages as having any formal information content – they are merely parts of clades.
Polyphyly	A polyphyletic assemblage is one which is neither monophyletic nor paraphyletic.	A polyphyletic assemblage is characterized by one or more homoplasies: character states which have converged or reverted so as to be the same but which have not been inherited from a common ancestor. No systematist recognizes polyphyletic assemblages as taxonomically meaningful entities, although ecologists sometimes consider them meaningful labels for functional participants in ecological communities (e. g., primary producers, detritivores, etc.).

Criticism

Cladistics, either generally or in specific applications, has been criticized from its beginnings. Decisions as to whether particular character states are homologous, a precondition of their being synapomorphies, have been challenged as involving circular reasoning and subjective judgements.^[29]
Transformed cladistics arose in the late 1970s in an attempt to resolve some of these problems by removing phylogeny from cladistic analysis, but it has remained unpopular.

However, homology is usually determined from analysis of the results that are evaluated with homology measures, mainly the CI (consistency index) and RI (retention index), which, it has been claimed,^{[by whom?]} makes the process objective. Also, homology can be equated to synapomorphy, which is what Patterson has done.^[30]

In disciplines other than biology

The comparisons used to acquire data on which cladograms can be based are not limited to the field of biology.^[31] Any group of individuals or classes that are hypothesized to have a common ancestor, and to which a set of common characteristics may or may not apply, can be compared pairwise. Cladograms can be used to depict the hypothetical descent relationships within groups of items in many different academic realms. The only requirement is that the items have characteristics that can be identified and measured.

Anthropology and archaeology:^[32] Cladistic methods have been used to reconstruct the development of cultures or artifacts using groups of cultural traits or artifact features.

Comparative mythology and folktale use cladistic methods to reconstruct the protoversion of many myths. Mythological phylogenies constructed with mythemes clearly support low horizontal transmissions (borrowings), historical (sometimes Palaeolithic) diffusions and punctuated evolution.^[33] They also are a powerful way to test hypotheses about cross-cultural relationships among folktales.^[34][35]

Literature: Cladistic methods have been used in the classification of the surviving manuscripts of the Canterbury Tales,^[36] and the manuscripts of the Sanskrit Charaka Samhita.^[37]

Historical linguistics:^[38] Cladistic methods have been used to reconstruct the phylogeny of languages using linguistic features. This is similar to the traditional comparative method of historical linguistics, but is more explicit in its use of parsimony and allows much faster analysis of large datasets (computational phylogenetics).

Textual criticism or stemmatics:^[37][39] Cladistic methods have been used to reconstruct the phylogeny of manuscripts of the same work (and reconstruct the lost original) using distinctive copying errors as apomorphies. This differs from traditional historical-comparative linguistics in enabling the editor to evaluate and place in genetic relationship large groups of manuscripts with large numbers of variants that would be impossible to handle manually. It also enables parsimony analysis of contaminated traditions of transmission that would be impossible to evaluate manually in a reasonable period of time.

Astrophysics^[40] infers the history of relationships between galaxies to create branching diagram hypotheses of galaxy diversification.