Sunspot

From Wikipedia, the free encyclopedia

Sunspots

Top: sunspot region 2192 during the partial solar eclipse in 2014[1] and sunspot region 1302 in September 2011. Middle: sunspot close-up in the visible spectrum (left) and in UV, taken by the TRACE observatory. Bottom: A large group of sunspots stretching about 320,000 km (200,000 mi) across.

Sunspots are temporary phenomena on the Sun's photosphere that appear as spots darker than the surrounding areas. They are regions of reduced surface temperature caused by concentrations of magnetic field flux that inhibit convection. Sunspots usually appear in pairs of opposite magnetic polarity.^[2] Their number varies according to the approximately 11-year solar cycle.

Individual sunspots or groups of sunspots may last anywhere from a few days to a few months, but eventually decay. Sunspots expand and contract as they move across the surface of the Sun, with diameters ranging from 16 km (10 mi)^[3] to 160,000 km (100,000 mi).^[4] The larger variety are visible from Earth without the aid of a telescope.^[5] They may travel at relative speeds, or proper motions, of a few hundred meters per second when they first emerge.

Indicating intense magnetic activity, sunspots accompany secondary phenomena such as coronal loops, prominences, and reconnection events. Most solar flares and coronal mass ejections originate in magnetically active regions around visible sunspot groupings. Similar phenomena indirectly observed on stars other than the Sun are commonly called starspots, and both light and dark spots have been measured.^[6]

History

Physics

Although they are at temperatures of roughly 3,000–4,500 K (2,700–4,200 °C), the contrast with the surrounding material at about 5,780 K (5,500 °C) leaves sunspots clearly visible as dark spots. This is because the luminance (which is essentially "brightness" in visible light) of a heated black body (closely approximated by the photosphere) at these temperatures varies extremely with temperature—considerably more so than the (temperature to the fourth power) variation in the total black-body radiation at all wavelengths (see Stefan–Boltzmann law). Isolated from the surrounding photosphere a sunspot would be brighter than the Moon.^[7]

Sunspots have two parts: the central umbra, which is the darkest part, where the magnetic field is approximately vertical (normal to the Sun's surface) and the surrounding penumbra, which is lighter, where the magnetic field is more inclined.

Lifecycle

Any given appearance of a sunspot may last anywhere from a few days to a few months, though groups of sunspots and their active regions tend to last weeks or months, but all do eventually decay and disappear. Sunspots expand and contract as they move across the surface of the Sun, with diameters ranging from 16 km (10 mi) to 160,000 km (100,000 mi).

Although the details of sunspot generation are still a matter of research, it appears that sunspots are the visible counterparts of magnetic flux tubes in the Sun's convective zone that get "wound up" by differential rotation. If the stress on the tubes reaches a certain limit, they curl up and puncture the Sun's surface. Convection is inhibited at the puncture points; the energy flux from the Sun's interior decreases, and with it, surface temperature.

The Wilson effect implies that sunspots are depressions on the Sun's surface. Observations using the Zeeman effect show that prototypical sunspots come in pairs with opposite magnetic polarity. From cycle to cycle, the polarities of leading and trailing (with respect to the solar rotation) sunspots change from north/south to south/north and back. Sunspots usually appear in groups.

Magnetic pressure should tend to remove field concentrations, causing the sunspots to disperse, but sunspot lifetimes are measured in days to weeks. In 2001, observations from the Solar and Heliospheric Observatory (SOHO) using sound waves traveling below the photosphere (local helioseismology) were used to develop a three-dimensional image of the internal structure below sunspots; these observations show that a powerful downdraft underneath each sunspot, forms a rotating vortex that sustains the concentrated magnetic field.^[8]

Solar cycle

Butterfly diagram showing paired Spörer's law behavior

Sunspot activity cycles are about every eleven years, with some variation in length. Over the solar cycle, sunspot populations rise quickly and then fall more slowly. The point of highest sunspot activity during a cycle is known as solar maximum, and the point of lowest activity as solar minimum. This period is also observed in most other solar activity and is linked to a variation in the solar magnetic field that changes polarity with this period.

Early in the cycle, sunspots appear in the higher latitudes and then move towards the equator as the cycle approaches maximum, following Spörer's law. Spots from two adjacent cycles can co-exist for some time. Spots from adjacent cycles can be distinguished by direction of their magnetic field.

The Wolf number sunspot index counts the average number of sunspots and groups of sunspots during specific intervals. The 11-year solar cycles are numbered sequentially, starting with the observations made in the 1750s.^[9]

George Ellery Hale first linked magnetic fields and sunspots in 1908.^[10] Hale suggested that the sunspot cycle period is 22 years, covering two periods of increased and decreased sunspot numbers, accompanied by polar reversals of the solar magnetic dipole field. Horace W. Babcock later proposed a qualitative model for the dynamics of the solar outer layers. The Babcock Model explains that magnetic fields cause the behavior described by Spörer's law, as well as other effects, which are twisted by the Sun's rotation.

Longer-period trends

Sunspot number also changes over long periods. For example, from 1900 to the 1960s, the solar maxima trend of sunspot count was upwards; for the following decades it diminished.^[11] However, the Sun was last as active as this period over 8,000 years ago.^[12]
Sunspots number is correlated with the intensity of solar radiation over the period since 1979, when satellite measurements became available. The variation caused by the sunspot cycle to solar output is relatively small, on the order of 0.1% of the solar constant (a peak-to-trough range of 1.3 W·m⁻² compared with 1366 W·m⁻² for the average solar constant).^[13][14]

400-year history of sunspot numbers, showing Maunder and

Dalton minima, and the Modern Maximum

Modern observation

The Swedish 1-m Solar Telescope at Roque de los Muchachos Observatory

Sunspots are observed with land-based and Earth-orbiting solar telescopes. These telescopes use filtration and projection techniques for direct observation, in addition to various types of filtered cameras. Specialized tools such as spectroscopes and spectrohelioscopes are used to examine sunspots and sunspot areas. Artificial eclipses allow viewing of the circumference of the Sun as sunspots rotate through the horizon.

ALMA observes a giant sunspot at 1.25 mm wavelength^[15]

Since looking directly at the Sun with the naked eye permanently damages human vision, amateur observation of sunspots is generally conducted using projected images, or directly through protective filters. Small sections of very dark filter glass, such as a #14 welder's glass, are effective. A telescope eyepiece can project the image, without filtration, onto a white screen where it can be viewed indirectly, and even traced, to follow sunspot evolution. Special purpose hydrogen-alpha narrow bandpass filters and aluminum-coated glass attenuation filters (which have the appearance of mirrors due to their extremely high optical density) on the front of a telescope provide safe observation through the eyepiece.

Application

Due to its link to other kinds of solar activity, sunspot occurrence can be used to help predict space weather, the state of the ionosphere, and hence the conditions of short-wave radio propagation or satellite communications. Solar activity (and the solar cycle) have been implicated in global warming, originally the role of the Maunder Minimum of sunspot occurrence in the Little Ice Age in European winter climate.^[16] Sunspots themselves, in terms of the magnitude of their radiant-energy deficit, have a weak effect on terrestrial climate^[17] in a direct sense. On longer time scales, such as the solar cycle, other magnetic phenomena (faculae and the chromospheric network) correlate with sunspot occurrence.^[18]

Starspot

In 1947, G. E. Kron proposed that starspots were the reason for periodic changes in brightness on red dwarfs.^[6] Since the mid-1990s, starspot observations have been made using increasingly powerful techniques yielding more and more detail: photometry showed starspot growth and decay and showed cyclic behavior similar to the Sun's; spectroscopy examined the structure of starspot regions by analyzing variations in spectral line splitting due to the Zeeman effect; Doppler imaging showed differential rotation of spots for several stars and distributions different from the Sun's; spectral line analysis measured the temperature range of spots and the stellar surfaces. For example, in 1999, Strassmeier reported the largest cool starspot ever seen rotating the giant K0 star XX Triangulum (HD 12545) with a temperature of 3,500 K (3,230 °C), together with a warm spot of 4,800 K (4,530 °C).^[6][19]

Gallery

• 

  Detail of a sunspot in 2005. The granulation of the Sun's surface can be seen clearly
  
• 

  Sunspots, September 2011.
  
• 

  A view of the coronal structure above a different sunspot seen in October 2010.
  
• 

  Sunspot 923 at sunset and in solar scope.
  
• 

  Sunset superior mirage of sunspot #930.
  
• 

  Sunset in Bangladesh, January 2004.
  
• 

  Tracking sunspots from Mars (animation; 8 July 2015).
  

Spline (mathematics)

From Wikipedia, the free encyclopedia

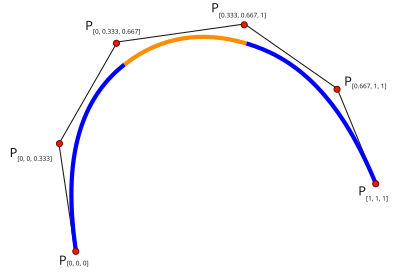
Single knots at 1/3 and 2/3 establish a spline of three cubic polynomials meeting with C² continuity. Triple knots at both ends of the interval ensure that the curve interpolates the end points

In mathematics, a spline is a special function defined piecewise by polynomials. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low degree polynomials, while avoiding Runge's phenomenon for higher degrees.

In the computer science subfields of computer-aided design and computer graphics, the term spline more frequently refers to a piecewise polynomial parametric curve^{[citation needed]}. Splines are popular curves in these subfields because of the simplicity of their construction, their ease and accuracy of evaluation, and their capacity to approximate complex shapes through curve fitting and interactive curve design^{[citation needed]}.

The term spline comes from the flexible spline devices used by shipbuilders and draftsmen to draw smooth shapes.^[1]

Introduction

The term "spline" is used to refer to a wide class of functions that are used in applications requiring data interpolation and/or smoothing. The data may be either one-dimensional or multi-dimensional. Spline functions for interpolation are normally determined as the minimizers of suitable measures of roughness (for example integral squared curvature) subject to the interpolation constraints.   Smoothing splines may be viewed as generalizations of interpolation splines where the functions are determined to minimize a weighted combination of the average squared approximation error over observed data and the roughness measure. For a number of meaningful definitions of the roughness measure, the spline functions are found to be finite dimensional in nature, which is the primary reason for their utility in computations and representation. For the rest of this section, we focus entirely on one-dimensional, polynomial splines and use the term "spline" in this restricted sense.

Definition

The simplest spline is a piecewise polynomial function, with each polynomial having a single variable. The spline S takes values from an interval [a,b] and maps them to ${\displaystyle \mathbb {R} }$, the set of real numbers,

${\displaystyle S:[a,b]\to \mathbb {R} .}$

Since S is piecewise defined, choose k subintervals to partition [a,b]:

${\displaystyle [t_{i},t_{i+1}]{\mbox{ , }}i=0,\ldots ,k-1}$

${\displaystyle [a,b]=[t_{0},t_{1}]\cup [t_{1},t_{2}]\cup \cdots \cup [t_{k-2},t_{k-1}]\cup [t_{k-1},t_{k}]}$

${\displaystyle a=t_{0}\leq t_{1}\leq \cdots \leq t_{k-1}\leq t_{k}=b}$

Each of these subintervals is associated with a polynomial P_i,

${\displaystyle P_{i}:[t_{i},t_{i+1}]\to \mathbb {R} }$.

On the ith subinterval of [a,b], S is defined by P_i,

${\displaystyle S(t)=P_{0}(t){\mbox{ , }}t_{0}\leq t$

${\displaystyle S(t)=P_{1}(t){\mbox{ , }}t_{1}\leq t$

${\displaystyle \vdots }$

${\displaystyle S(t)=P_{k-1}(t){\mbox{ , }}t_{k-1}\leq t\leq t_{k}.}$

The given k+1 points t_j (0 ≤ j ≤ k) are called knots. The vector ${\displaystyle {\mathbf {t}}=(t_{0},\dots ,t_{k})}$ is called a knot vector for the spline. If the knots are equidistantly distributed in the interval [a,b] we say the spline is uniform, otherwise we say it is non-uniform.

If the k polynomial pieces P_i each have degree at most n, then the spline is said to be of degree ≤ n (or of order ≤ n+1).

If for ${\displaystyle 1\leq i\leq k-1\;:\;S\in C^{r_{i}}}$ in a neighborhood of the k-1 points t_i, then the spline is said to be of smoothness (at least) ${\displaystyle C^{r_{i}}}$ at t_i. That is, at t_i the two pieces P_i−1 and P_i share common derivative values from the derivative of order 0 (the function value) up through the derivative of order r_i (in other words, the two adjacent polynomial pieces connect with loss of smoothness of at most n - r_i).

A vector ${\displaystyle {\mathbf {r}}=(r_{1},\dots ,r_{k-1})}$ such that the spline has smoothness ${\displaystyle C^{r_{i}}}$ at t_i for ${\displaystyle i=1,\ldots ,k-1}$ is called a smoothness vector for the spline.

Given a knot vector ${\displaystyle {\mathbf {t}}}$, a degree n, and a smoothness vector ${\displaystyle {\mathbf {r}}}$ for ${\displaystyle {\mathbf {t}}}$, one can consider the set of all splines of degree ${\displaystyle \leq n}$ having knot vector ${\displaystyle {\mathbf {t}}}$ and smoothness vector ${\displaystyle {\mathbf {r}}}$. Equipped with the operation of adding two functions (pointwise addition) and taking real multiples of functions, this set becomes a real vector space. This spline space is commonly denoted by ${\displaystyle S_{n}^{\mathbf {r}}({\mathbf {t}})}$.

A knot t_i can be "deleted" by moving it to equal another knot t_i+1. The polynomial piece P_i(t) disappears, and the pieces P_i−1(t) and P_i+1(t) join with the sum of the continuity losses for t_i and t_i+1. That is,

${\displaystyle S(t)\in C^{n-j_{i}-j_{i+1}}[t_{i}=t_{i+1}],}$ where ${\displaystyle j_{i}=n-r_{i}}$

This leads to a more general understanding of a knot vector. The continuity loss at any point can be considered to be the result of multiple knots located at that point, and a spline type can be completely characterized by its degree n and its extended knot vector

${\displaystyle (t_{0},t_{1},\cdots ,t_{1},t_{2},\cdots ,t_{2},t_{3},\cdots ,t_{k-2},t_{k-1},\cdots ,t_{k-1},t_{k})}$

where t_i is repeated j_i times for ${\displaystyle i=1,\dots ,k-1}$.

A parametric curve on the interval [a,b]

${\displaystyle G(t)=(X(t),Y(t)){\mbox{ , }}t\in [a,b]}$

is a spline curve if both X and Y are spline functions of the same degree with the same extended knot vectors on that interval.

Examples

Suppose the interval [a,b] is [0,3] and the subintervals are [0,1], [1,2], and [2,3]. Suppose the polynomial pieces are to be of degree 2, and the pieces on [0,1] and [1,2] must join in value and first derivative (at t=1) while the pieces on [1,2] and [2,3] join simply in value (at t = 2). This would define a type of spline S(t) for which

${\displaystyle S(t)=P_{0}(t)=-1+4t-t^{2}{\mbox{ , }}0\leq t<1 annotation="">$

${\displaystyle S(t)=P_{1}(t)=2t{\mbox{ , }}1\leq t<2 annotation="">$

${\displaystyle S(t)=P_{2}(t)=2-t+t^{2}{\mbox{ , }}2\leq t\leq 3}$

would be a member of that type, and also

${\displaystyle S(t)=P_{0}(t)=-2-2t^{2}{\mbox{ , }}0\leq t<1 annotation="">$

${\displaystyle S(t)=P_{1}(t)=1-6t+t^{2}{\mbox{ , }}1\leq t<2 annotation="">$

${\displaystyle S(t)=P_{2}(t)=-1+t-2t^{2}{\mbox{ , }}2\leq t\leq 3}$

would be a member of that type. (Note: while the polynomial piece 2t is not quadratic, the result is still called a quadratic spline. This demonstrates that the degree of a spline is the maximum degree of its polynomial parts.) The extended knot vector for this type of spline would be (0, 1, 2, 2, 3).

The simplest spline has degree 0. It is also called a step function. The next most simple spline has degree 1. It is also called a linear spline. A closed linear spline (i.e, the first knot and the last are the same) in the plane is just a polygon.

A common spline is the natural cubic spline of degree 3 with continuity C². The word "natural" means that the second derivatives of the spline polynomials are set equal to zero at the endpoints of the interval of interpolation

${\displaystyle S''(a)\,=S''(b)=0.}$

Algorithm for computing natural cubic splines

Cubic splines have polynomial pieces of the form
${\displaystyle P_{i}(x)=a_{i}+b_{i}(x-x_{i})+c_{i}(x-x_{i})^{2}+d_{i}(x-x_{i})^{3}.}$ Given ${\displaystyle k+1}$ coordinates ${\displaystyle (x_{0},y_{0}),(x_{1},y_{1}),\dots ,(x_{k},y_{k}),}$ we find ${\displaystyle k}$ polynomials ${\displaystyle P_{i}(x),}$ which satisfy for ${\displaystyle 1\leq i\leq k-1}$:

${\displaystyle P_{0}(x_{0})=y_{0}\quad }$ and ${\displaystyle \quad P_{i-1}(x_{i})=y_{i}=P_{i}(x_{i}),}$

${\displaystyle P'_{i-1}(x_{i})=P'_{i}(x_{i}),}$

${\displaystyle P''_{i-1}(x_{i})=P''_{i}(x_{i}),}$

${\displaystyle P''_{0}(x_{0})=P''_{k-1}(x_{k})=0.}$

One such polynomial ${\displaystyle P_{i}}$ is given by a 5-tuple ${\displaystyle (a,b,c,d,x)}$ where ${\displaystyle a,b,c\,}$ and ${\displaystyle d\,}$ correspond to the coefficients as used above and ${\displaystyle x}$ denotes the variable over the appropriate domain ${\displaystyle [x_{i},x_{i+1}]}$.

Computation of Natural Cubic Splines:

Input: a set of ${\displaystyle k+1}$ coordinates

Output: a spline as a set of polynomial pieces, each represented by a 5-tuple.

1. Create a new array a of size k + 1, and for ${\displaystyle i=0,\ldots ,k}$ set ${\displaystyle a_{i}=y_{i}}$
2. Create new arrays b, d and μ each of size k
3. Create a new array h of size k and for ${\displaystyle i=0,\ldots ,k-1}$ set ${\displaystyle h_{i}=x_{i+1}-x_{i}}$
4. Create a new array α of size k-1 and for ${\displaystyle i=1,\ldots ,k-1}$ set ${\displaystyle \alpha _{i}={\tfrac {3}{h_{i}}}(a_{i+1}-a_{i})-{\tfrac {3}{h_{i-1}}}(a_{i}-a_{i-1})}$
5. Create new arrays c, l, and z each of size ${\displaystyle k+1}$.
6. Set ${\displaystyle l_{0}=1,\;\mu _{0}=z_{0}=0}$
7. For ${\displaystyle i=1,\ldots ,k-1\,}$
   1. Set ${\displaystyle l_{i}=2(x_{i+1}-x_{i-1})-h_{i-1}\mu _{i-1}.}$
   2. Set ${\displaystyle \mu _{i}={\tfrac {h_{i}}{l_{i}}}.}$
   3. Set ${\displaystyle z_{i}={\tfrac {\alpha _{i}-h_{i-1}z_{i-1}}{l_{i}}}.}$
8. Set ${\displaystyle l_{k}=1;z_{k}=c_{k}=0.}$
9. For ${\displaystyle j=k-1,k-2,\ldots ,0}$
   1. Set ${\displaystyle c_{j}=z_{j}-\mu _{j}c_{j+1}}$
   2. Set ${\displaystyle b_{j}={\tfrac {a_{j+1}-a_{j}}{h_{j}}}-{\tfrac {h_{j}(c_{j+1}+2c_{j})}{3}}}$
   3. Set ${\displaystyle d_{j}={\tfrac {c_{j+1}-c_{j}}{3h_{j}}}.}$
10. Create the spline as a new set of polynomials and call it output_set. Populate it with k 5-tuples for the polynomials P.
11. For ${\displaystyle i=0,\ldots ,k-1}$
    1. Set P_i,a = a_i
    2. Set P_i,b = b_i
    3. Set P_i,c = c_i
    4. Set P_i,d = d_i
    5. Set P_i,x = x_i
12. Output output_set

Continuity levels

If sampled data from a function or a physical object are available, spline interpolation is an approach to creating a spline that approximates those data.

Natural continuity

The classical spline type of degree n used in numerical analysis has continuity

${\displaystyle S(t)\in \mathrm {C} ^{n-1}[a,b],\,}$

which means that every two adjacent polynomial pieces meet in their value and first n - 1 derivatives at each knot. The mathematical spline that most closely models the flat spline is a cubic (n = 3), twice continuously differentiable (C²), natural spline, which is a spline of this classical type with additional conditions imposed at endpoints a and b.

Reduced continuity

Another type of spline that is much used in graphics, for example in drawing programs such as Adobe Illustrator from Adobe Systems, has pieces that are cubic but has continuity only at most

${\displaystyle S(t)\in \mathrm {C} ^{1}[a,b].}$

This spline type is also used in PostScript as well as in the definition of some computer typographic fonts.

Many computer-aided design systems that are designed for high-end graphics and animation use extended knot vectors, for example Maya from Alias. Computer-aided design systems often use an extended concept of a spline known as a Nonuniform rational B-spline (NURBS).

Locally negative continuity

It might be asked what meaning more than n multiple knots in a knot vector have, since this would lead to continuities like

${\displaystyle S(t)\in C^{-m}{\mbox{ , }}m>0}$

at the location of this high multiplicity. By convention, any such situation indicates a simple discontinuity between the two adjacent polynomial pieces. This means that if a knot t_i appears more than n + 1 times in an extended knot vector, all instances of it in excess of the (n + 1)th can be removed without changing the character of the spline, since all multiplicities n + 1, n + 2, n + 3, etc. have the same meaning. It is commonly assumed that any knot vector defining any type of spline has been culled in this fashion.

General expression for a C² interpolating cubic spline

The general expression for the ith C² interpolating cubic spline at a point x with the natural condition can be found using the formula

${\displaystyle S_{i}(x)={\frac {z_{i}(x-t_{i-1})^{3}}{6h_{i}}}+{\frac {z_{i-1}(t_{i}-x)^{3}}{6h_{i}}}+\left[{\frac {f(t_{i})}{h_{i}}}-{\frac {z_{i}h_{i}}{6}}\right](x-t_{i-1})+\left[{\frac {f(t_{i-1})}{h_{i}}}-{\frac {z_{i-1}h_{i}}{6}}\right](t_{i}-x)}$

where

• ${\displaystyle z_{i}=f^{\prime \prime }(t_{i})}$ are the values of the second derivative at the ith knot.
• ${\displaystyle h_{i}^{}=t_{i}-t_{i-1}}$
• ${\displaystyle f(t_{i}^{})}$ are the values of the function at the ith knot.

Representations and names

For a given interval [a,b] and a given extended knot vector on that interval, the splines of degree n form a vector space. Briefly this means that adding any two splines of a given type produces spline of that given type, and multiplying a spline of a given type by any constant produces a spline of that given type. The dimension of the space containing all splines of a certain type can be counted from the extended knot vector:

${\displaystyle a=t_{0}<\underbrace {t_{1}=\cdots =t_{1}} _{j_{1}}<\cdots <\underbrace {t_{k-2}=\cdots =t_{k-2}} _{j_{k-2}}$

${\displaystyle j_{i}\leq n+1~,~~i=1,\ldots ,k-2.}$

The dimension is equal to the sum of the degree plus the multiplicities

${\displaystyle d=n+\sum _{i=1}^{k-2}j_{i}.}$

If a type of spline has additional linear conditions imposed upon it, then the resulting spline will lie in a subspace. The space of all natural cubic splines, for instance, is a subspace of the space of all cubic C² splines.

The literature of splines is replete with names for special types of splines. These names have been associated with:

• The choices made for representing the spline, for example:
  • using basis functions for the entire spline (giving us the name B-splines)
  • using Bernstein polynomials as employed by Pierre Bézier to represent each polynomial piece (giving us the name Bézier splines)
• The choices made in forming the extended knot vector, for example:
  • using single knots for C^n-1 continuity and spacing these knots evenly on [a,b] (giving us uniform splines)
  • using knots with no restriction on spacing (giving us nonuniform splines)
• Any special conditions imposed on the spline, for example:
  • enforcing zero second derivatives at a and b (giving us natural splines)
  • requiring that given data values be on the spline (giving us interpolating splines)

Often a special name was chosen for a type of spline satisfying two or more of the main items above. For example, the Hermite spline is a spline that is expressed using Hermite polynomials to represent each of the individual polynomial pieces. These are most often used with n = 3; that is, as Cubic Hermite splines. In this degree they may additionally be chosen to be only tangent-continuous (C¹); which implies that all interior knots are double. Several methods have been invented to fit such splines to given data points; that is, to make them into interpolating splines, and to do so by estimating plausible tangent values where each two polynomial pieces meet (giving us Cardinal splines, Catmull-Rom splines, and Kochanek-Bartels splines, depending on the method used).

For each of the representations, some means of evaluation must be found so that values of the spline can be produced on demand. For those representations that express each individual polynomial piece P_i(t) in terms of some basis for the degree n polynomials, this is conceptually straightforward:

• For a given value of the argument t, find the interval in which it lies ${\displaystyle t\in [t_{i},t_{i+1}]}$
• Look up the polynomial basis chosen for that interval ${\displaystyle P_{0},\ldots ,P_{k-2}}$
• Find the value of each basis polynomial at t: ${\displaystyle P_{0}(t),\ldots ,P_{k-2}(t)}$
• Look up the coefficients of the linear combination of those basis polynomials that give the spline on that interval c₀, ..., c_k-2
• Add up that linear combination of basis polynomial values to get the value of the spline at t:

${\displaystyle \sum _{j=0}^{k-2}c_{j}P_{j}(t).}$

However, the evaluation and summation steps are often combined in clever ways. For example, Bernstein polynomials are a basis for polynomials that can be evaluated in linear combinations efficiently using special recurrence relations. This is the essence of De Casteljau's algorithm, which features in Bézier curves and Bézier splines.

For a representation that defines a spline as a linear combination of basis splines, however, something more sophisticated is needed. The de Boor algorithm is an efficient method for evaluating B-splines.

History

Before computers were used, numerical calculations were done by hand. Although piecewise-defined functions like the sign function or step function were used, polynomials were generally preferred because they were easier to work with. Through the advent of computers splines have gained importance. They were first used as a replacement for polynomials in interpolation, then as a tool to construct smooth and flexible shapes in computer graphics.

A wooden spline

It is commonly accepted that the first mathematical reference to splines is the 1946 paper by Schoenberg, which is probably the first place that the word "spline" is used in connection with smooth, piecewise polynomial approximation. However, the ideas have their roots in the aircraft and shipbuilding industries. In the foreword to (Bartels et al., 1987), Robin Forrest describes "lofting", a technique used in the British aircraft industry during World War II to construct templates for airplanes by passing thin wooden strips (called "splines") through points laid out on the floor of a large design loft, a technique borrowed from ship-hull design. For years the practice of ship design had employed models to design in the small. The successful design was then plotted on graph paper and the key points of the plot were re-plotted on larger graph paper to full size. The thin wooden strips provided an interpolation of the key points into smooth curves. The strips would be held in place at discrete points (called "ducks" by Forrest; Schoenberg used "dogs" or "rats") and between these points would assume shapes of minimum strain energy. According to Forrest, one possible impetus for a mathematical model for this process was the potential loss of the critical design components for an entire aircraft should the loft be hit by an enemy bomb. This gave rise to "conic lofting", which used conic sections to model the position of the curve between the ducks. Conic lofting was replaced by what we would call splines in the early 1960s based on work by J. C. Ferguson at Boeing and (somewhat later) by M. A. Sabin at British Aircraft Corporation.

The word "spline" was originally an East Anglian dialect word.^{[citation needed]}

The use of splines for modeling automobile bodies seems to have several independent beginnings. Credit is claimed on behalf of de Casteljau at Citroën, Pierre Bézier at Renault, and Birkhoff, Garabedian, and de Boor at General Motors (see Birkhoff and de Boor, 1965), all for work occurring in the very early 1960s or late 1950s. At least one of de Casteljau's papers was published, but not widely, in 1959. De Boor's work at General Motors resulted in a number of papers being published in the early 1960s, including some of the fundamental work on B-splines.

Work was also being done at Pratt & Whitney Aircraft, where two of the authors of (Ahlberg et al., 1967)—the first book-length treatment of splines—were employed, and the David Taylor Model Basin, by Feodor Theilheimer. The work at General Motors is detailed nicely in (Birkhoff, 1990) and (Young, 1997). Davis (1997) summarizes some of this material.