In mathematics and mathematical logic, Boolean algebra is the branch of algebra in which the values of the variables are the truth values true and false, usually denoted 1 and 0 respectively. Instead of elementary algebra where the values of the variables are numbers, and the prime operations are addition and multiplication, the main operations of Boolean algebra are the conjunction and denoted as ∧, the disjunction or denoted as ∨, and the negation not denoted as ¬. It is thus a formalism for describing logical relations in the same way that ordinary algebra describes numeric relations.
Boolean algebra was introduced by George Boole in his first book The Mathematical Analysis of Logic (1847), and set forth more fully in his An Investigation of the Laws of Thought (1854).[1] According to Huntington, the term "Boolean algebra" was first suggested by Sheffer in 1913,[2] although Charles Sanders Peirce in 1880 gave the title "A Boolian Algebra with One Constant" to the first chapter of his "The Simplest Mathematics".[3] Boolean algebra has been fundamental in the development of digital electronics, and is provided for in all modern programming languages. It is also used in set theory and statistics.[4]
History
In the 1930s, while studying switching circuits, Claude Shannon observed that one could also apply the rules of Boole's algebra in this setting, and he introduced switching algebra as a way to analyze and design circuits by algebraic means in terms of logic gates. Shannon already had at his disposal the abstract mathematical apparatus, thus he cast his switching algebra as the two-element Boolean algebra. In circuit engineering settings today, there is little need to consider other Boolean algebras, thus "switching algebra" and "Boolean algebra" are often used interchangeably.[6][7][8] Efficient implementation of Boolean functions is a fundamental problem in the design of combinational logic circuits. Modern electronic design automation tools for VLSI circuits often rely on an efficient representation of Boolean functions known as (reduced ordered) binary decision diagrams (BDD) for logic synthesis and formal verification.[9]
Logic sentences that can be expressed in classical propositional calculus have an equivalent expression in Boolean algebra. Thus, Boolean logic is sometimes used to denote propositional calculus performed in this way.[10][11][12] Boolean algebra is not sufficient to capture logic formulas using quantifiers, like those from first order logic. Although the development of mathematical logic did not follow Boole's program, the connection between his algebra and logic was later put on firm ground in the setting of algebraic logic, which also studies the algebraic systems of many other logics.[5] The problem of determining whether the variables of a given Boolean (propositional) formula can be assigned in such a way as to make the formula evaluate to true is called the Boolean satisfiability problem (SAT), and is of importance to theoretical computer science, being the first problem shown to be NP-complete. The closely related model of computation known as a Boolean circuit relates time complexity (of an algorithm) to circuit complexity.
Values
Whereas in elementary algebra expressions denote mainly numbers, in Boolean algebra they denote the truth values false and true. These values are represented with the bits (or binary digits), namely 0 and 1. They do not behave like the integers 0 and 1, for which 1 + 1 = 2, but may be identified with the elements of the two-element field GF(2), that is, integer arithmetic modulo 2, for which 1 + 1 = 0. Addition and multiplication then play the Boolean roles of XOR (exclusive-or) and AND (conjunction) respectively, with disjunction x∨y (inclusive-or) definable as x + y - xy.Boolean algebra also deals with functions which have their values in the set {0, 1}. A sequence of bits is a commonly used such function. Another common example is the subsets of a set E: to a subset F of E is associated the indicator function that takes the value 1 on F and 0 outside F. The most general example is the elements of a Boolean algebra, with all of the foregoing being instances thereof.
As with elementary algebra, the purely equational part of the theory may be developed without considering explicit values for the variables.[13]
Operations
Basic operations
The basic operations of Boolean algebra are as follows:- AND (conjunction), denoted x∧y (sometimes x AND y or Kxy), satisfies x∧y = 1 if x = y = 1 and x∧y = 0 otherwise.
- OR (disjunction), denoted x∨y (sometimes x OR y or Axy), satisfies x∨y = 0 if x = y = 0 and x∨y = 1 otherwise.
- NOT (negation), denoted ¬x (sometimes NOT x, Nx or !x), satisfies ¬x = 0 if x = 1 and ¬x = 1 if x = 0.
-
0 0 0 0 1 0 0 1 0 1 0 1 1 1 1 1
0 1 1 0
Secondary operations
The three Boolean operations described above are referred to as basic, meaning that they can be taken as a basis for other Boolean operations that can be built up from them by composition, the manner in which operations are combined or compounded. Operations composed from the basic operations include the following examples:0 0 1 0 1 1 0 0 1 0 0 1 1 1 0 1 1 1 0 1
The second operation, x ⊕ y, or Jxy, is called exclusive or (often abbreviated as XOR) to distinguish it from disjunction as the inclusive kind. It excludes the possibility of both x and y. Defined in terms of arithmetic it is addition mod 2 where 1 + 1 = 0.
The third operation, the complement of exclusive or, is equivalence or Boolean equality: x ≡ y, or Exy, is true just when x and y have the same value. Hence x ⊕ y as its complement can be understood as x ≠ y, being true just when x and y are different. Equivalence's counterpart in arithmetic mod 2 is x + y + 1.
Given two operands, each with two possible values, there are 22 = 4 possible combinations of inputs. Because each output can have two possible values, there are a total of 24 = 16 possible binary Boolean operations.
Laws
A law of Boolean algebra is an identity such as x∨(y∨z) = (x∨y)∨z between two Boolean terms, where a Boolean term is defined as an expression built up from variables and the constants 0 and 1 using the operations ∧, ∨, and ¬. The concept can be extended to terms involving other Boolean operations such as ⊕, →, and ≡, but such extensions are unnecessary for the purposes to which the laws are put. Such purposes include the definition of a Boolean algebra as any model of the Boolean laws, and as a means for deriving new laws from old as in the derivation of x∨(y∧z) = x∨(z∧y) from y∧z = z∧y as treated in the section on axiomatization.Monotone laws
Boolean algebra satisfies many of the same laws as ordinary algebra when one matches up ∨ with addition and ∧ with multiplication. In particular the following laws are common to both kinds of algebra:[14]Associativity of :
Associativity of :
Commutativity of :
Commutativity of :
Distributivity of over
:
Identity for :
Identity for :
Annihilator for :
Annihilator for :
Idempotence of :
Idempotence of :
Absorption 1: Absorption 2: Distributivity of over
:
All of the laws treated so far have been for conjunction and disjunction. These operations have the property that changing either argument either leaves the output unchanged or the output changes in the same way as the input. Equivalently, changing any variable from 0 to 1 never results in the output changing from 1 to 0. Operations with this property are said to be monotone. Thus the axioms so far have all been for monotonic Boolean logic. Nonmonotonicity enters via complement ¬ as follows.[4]
Nonmonotone laws
The complement operation is defined by the following two laws.In both ordinary and Boolean algebra, negation works by exchanging pairs of elements, whence in both algebras it satisfies the double negation law (also called involution law):
Completeness
The laws listed above define Boolean algebra, in the sense that they entail the rest of the subject. The laws Complementation 1 and 2, together with the monotone laws, suffice for this purpose and can therefore be taken as one possible complete set of laws or axiomatization of Boolean algebra. Every law of Boolean algebra follows logically from these axioms. Furthermore, Boolean algebras can then be defined as the models of these axioms as treated in the section thereon.To clarify, writing down further laws of Boolean algebra cannot give rise to any new consequences of these axioms, nor can it rule out any model of them. In contrast, in a list of some but not all of the same laws, there could have been Boolean laws that did not follow from those on the list, and moreover there would have been models of the listed laws that were not Boolean algebras.
This axiomatization is by no means the only one, or even necessarily the most natural given that we did not pay attention to whether some of the axioms followed from others but simply chose to stop when we noticed we had enough laws, treated further in the section on axiomatizations. Or the intermediate notion of axiom can be sidestepped altogether by defining a Boolean law directly as any tautology, understood as an equation that holds for all values of its variables over 0 and 1. All these definitions of Boolean algebra can be shown to be equivalent.
Duality principle
Principle: If {X, R} is a poset, then {X, R(inverse)} is also a poset.There is nothing magical about the choice of symbols for the values of Boolean algebra. We could rename 0 and 1 to say α and β, and as long as we did so consistently throughout it would still be Boolean algebra, albeit with some obvious cosmetic differences.
But suppose we rename 0 and 1 to 1 and 0 respectively. Then it would still be Boolean algebra, and moreover operating on the same values. However it would not be identical to our original Boolean algebra because now we find ∨ behaving the way ∧ used to do and vice versa. So there are still some cosmetic differences to show that we've been fiddling with the notation, despite the fact that we're still using 0s and 1s.
But if in addition to interchanging the names of the values we also interchange the names of the two binary operations, now there is no trace of what we have done. The end product is completely indistinguishable from what we started with. We might notice that the columns for x∧y and x∨y in the truth tables had changed places, but that switch is immaterial.
When values and operations can be paired up in a way that leaves everything important unchanged when all pairs are switched simultaneously, we call the members of each pair dual to each other. Thus 0 and 1 are dual, and ∧ and ∨ are dual. The Duality Principle, also called De Morgan duality, asserts that Boolean algebra is unchanged when all dual pairs are interchanged.
One change we did not need to make as part of this interchange was to complement. We say that complement is a self-dual operation. The identity or do-nothing operation x (copy the input to the output) is also self-dual. A more complicated example of a self-dual operation is (x∧y) ∨ (y∧z) ∨ (z∧x). There is no self-dual binary operation that depends on both its arguments. A composition of self-dual operations is a self-dual operation. For example, if f(x, y, z) = (x∧y) ∨ (y∧z) ∨ (z∧x), then f(f(x, y, z), x, t) is a self-dual operation of four arguments x,y,z,t.
The principle of duality can be explained from a group theory perspective by the fact that there are exactly four functions that are one-to-one mappings (automorphisms) of the set of Boolean polynomials back to itself: the identity function, the complement function, the dual function and the contradual function (complemented dual). These four functions form a group under function composition, isomorphic to the Klein four-group, acting on the set of Boolean polynomials. Walter Gottschalk remarked that consequently a more appropriate name for the phenomenon would be the principle (or square) of quaternality.[15]
Diagrammatic representations
Venn diagrams
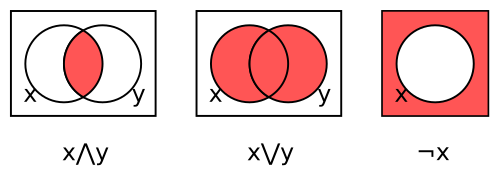
A Venn diagram[16] is a representation of a Boolean operation using shaded overlapping regions. There is one region for each variable, all circular in the examples here. The interior and exterior of region x corresponds respectively to the values 1 (true) and 0 (false) for variable x. The shading indicates the value of the operation for each combination of regions, with dark denoting 1 and light 0 (some authors use the opposite convention).The three Venn diagrams in the figure below represent respectively conjunction x∧y, disjunction x∨y, and complement ¬x.
Figure 2. Venn diagrams for conjunction, disjunction, and complement
For conjunction, the region inside both circles is shaded to indicate that x∧y is 1 when both variables are 1. The other regions are left unshaded to indicate that x∧y is 0 for the other three combinations.
The second diagram represents disjunction x∨y by shading those regions that lie inside either or both circles. The third diagram represents complement ¬x by shading the region not inside the circle.
While we have not shown the Venn diagrams for the constants 0 and 1, they are trivial, being respectively a white box and a dark box, neither one containing a circle. However we could put a circle for x in those boxes, in which case each would denote a function of one argument, x, which returns the same value independently of x, called a constant function. As far as their outputs are concerned, constants and constant functions are indistinguishable; the difference is that a constant takes no arguments, called a zeroary or nullary operation, while a constant function takes one argument, which it ignores, and is a unary operation.
Venn diagrams are helpful in visualizing laws. The commutativity laws for ∧ and ∨ can be seen from the symmetry of the diagrams: a binary operation that was not commutative would not have a symmetric diagram because interchanging x and y would have the effect of reflecting the diagram horizontally and any failure of commutativity would then appear as a failure of symmetry.
Idempotence of ∧ and ∨ can be visualized by sliding the two circles together and noting that the shaded area then becomes the whole circle, for both ∧ and ∨.
To see the first absorption law, x∧(x∨y) = x, start with the diagram in the middle for x∨y and note that the portion of the shaded area in common with the x circle is the whole of the x circle. For the second absorption law, x∨(x∧y) = x, start with the left diagram for x∧y and note that shading the whole of the x circle results in just the x circle being shaded, since the previous shading was inside the x circle.
The double negation law can be seen by complementing the shading in the third diagram for ¬x, which shades the x circle.
To visualize the first De Morgan's law, (¬x)∧(¬y) = ¬(x∨y), start with the middle diagram for x∨y and complement its shading so that only the region outside both circles is shaded, which is what the right hand side of the law describes. The result is the same as if we shaded that region which is both outside the x circle and outside the y circle, i.e. the conjunction of their exteriors, which is what the left hand side of the law describes.
The second De Morgan's law, (¬x)∨(¬y) = ¬(x∧y), works the same way with the two diagrams interchanged.
The first complement law, x∧¬x = 0, says that the interior and exterior of the x circle have no overlap. The second complement law, x∨¬x = 1, says that everything is either inside or outside the x circle.
Digital logic gates
Digital logic is the application of the Boolean algebra of 0 and 1 to electronic hardware consisting of logic gates connected to form a circuit diagram. Each gate implements a Boolean operation, and is depicted schematically by a shape indicating the operation. The shapes associated with the gates for conjunction (AND-gates), disjunction (OR-gates), and complement (inverters) are as follows.The lines on the left of each gate represent input wires or ports. The value of the input is represented by a voltage on the lead. For so-called "active-high" logic, 0 is represented by a voltage close to zero or "ground", while 1 is represented by a voltage close to the supply voltage; active-low reverses this. The line on the right of each gate represents the output port, which normally follows the same voltage conventions as the input ports.
Complement is implemented with an inverter gate. The triangle denotes the operation that simply copies the input to the output; the small circle on the output denotes the actual inversion complementing the input. The convention of putting such a circle on any port means that the signal passing through this port is complemented on the way through, whether it is an input or output port.
The Duality Principle, or De Morgan's laws, can be understood as asserting that complementing all three ports of an AND gate converts it to an OR gate and vice versa, as shown in Figure 4 below. Complementing both ports of an inverter however leaves the operation unchanged.
More generally one may complement any of the eight subsets of the three ports of either an AND or OR gate. The resulting sixteen possibilities give rise to only eight Boolean operations, namely those with an odd number of 1's in their truth table. There are eight such because the "odd-bit-out" can be either 0 or 1 and can go in any of four positions in the truth table. There being sixteen binary Boolean operations, this must leave eight operations with an even number of 1's in their truth tables. Two of these are the constants 0 and 1 (as binary operations that ignore both their inputs); four are the operations that depend nontrivially on exactly one of their two inputs, namely x, y, ¬x, and ¬y; and the remaining two are x⊕y (XOR) and its complement x≡y.
Boolean algebras
The term "algebra" denotes both a subject, namely the subject of algebra, and an object, namely an algebraic structure. Whereas the foregoing has addressed the subject of Boolean algebra, this section deals with mathematical objects called Boolean algebras, defined in full generality as any model of the Boolean laws. We begin with a special case of the notion definable without reference to the laws, namely concrete Boolean algebras, and then give the formal definition of the general notion.Concrete Boolean algebras
A concrete Boolean algebra or field of sets is any nonempty set of subsets of a given set X closed under the set operations of union, intersection, and complement relative to X.[4](As an aside, historically X itself was required to be nonempty as well to exclude the degenerate or one-element Boolean algebra, which is the one exception to the rule that all Boolean algebras satisfy the same equations since the degenerate algebra satisfies every equation. However this exclusion conflicts with the preferred purely equational definition of "Boolean algebra," there being no way to rule out the one-element algebra using only equations— 0 ≠ 1 does not count, being a negated equation. Hence modern authors allow the degenerate Boolean algebra and let X be empty.)
Example 1. The power set 2X of X, consisting of all subsets of X. Here X may be any set: empty, finite, infinite, or even uncountable.
Example 2. The empty set and X. This two-element algebra shows that a concrete Boolean algebra can be finite even when it consists of subsets of an infinite set. It can be seen that every field of subsets of X must contain the empty set and X. Hence no smaller example is possible, other than the degenerate algebra obtained by taking X to be empty so as to make the empty set and X coincide.
Example 3. The set of finite and cofinite sets of integers, where a cofinite set is one omitting only finitely many integers. This is clearly closed under complement, and is closed under union because the union of a cofinite set with any set is cofinite, while the union of two finite sets is finite. Intersection behaves like union with "finite" and "cofinite" interchanged.
Example 4. For a less trivial example of the point made by Example 2, consider a Venn diagram formed by n closed curves partitioning the diagram into 2n regions, and let X be the (infinite) set of all points in the plane not on any curve but somewhere within the diagram. The interior of each region is thus an infinite subset of X, and every point in X is in exactly one region. Then the set of all 22n possible unions of regions (including the empty set obtained as the union of the empty set of regions and X obtained as the union of all 2n regions) is closed under union, intersection, and complement relative to X and therefore forms a concrete Boolean algebra. Again we have finitely many subsets of an infinite set forming a concrete Boolean algebra, with Example 2 arising as the case n = 0 of no curves.
Subsets as bit vectors
A subset Y of X can be identified with an indexed family of bits with index set X, with the bit indexed by x ∈ X being 1 or 0 according to whether or not x ∈ Y. (This is the so-called characteristic function notion of a subset.) For example, a 32-bit computer word consists of 32 bits indexed by the set {0,1,2,…,31}, with 0 and 31 indexing the low and high order bits respectively. For a smaller example, if X = {a,b,c} where a, b, c are viewed as bit positions in that order from left to right, the eight subsets {}, {c}, {b}, {b,c}, {a}, {a,c}, {a,b}, and {a,b,c} of X can be identified with the respective bit vectors 000, 001, 010, 011, 100, 101, 110, and 111. Bit vectors indexed by the set of natural numbers are infinite sequences of bits, while those indexed by the reals in the unit interval [0,1] are packed too densely to be able to write conventionally but nonetheless form well-defined indexed families (imagine coloring every point of the interval [0,1] either black or white independently; the black points then form an arbitrary subset of [0,1]).From this bit vector viewpoint, a concrete Boolean algebra can be defined equivalently as a nonempty set of bit vectors all of the same length (more generally, indexed by the same set) and closed under the bit vector operations of bitwise ∧, ∨, and ¬, as in 1010∧0110 = 0010, 1010∨0110 = 1110, and ¬1010 = 0101, the bit vector realizations of intersection, union, and complement respectively.
The prototypical Boolean algebra
The set {0,1} and its Boolean operations as treated above can be understood as the special case of bit vectors of length one, which by the identification of bit vectors with subsets can also be understood as the two subsets of a one-element set. We call this the prototypical Boolean algebra, justified by the following observation.- The laws satisfied by all nondegenerate concrete Boolean algebras coincide with those satisfied by the prototypical Boolean algebra.
The final goal of the next section can be understood as eliminating "concrete" from the above observation. We shall however reach that goal via the surprisingly stronger observation that, up to isomorphism, all Boolean algebras are concrete.
Boolean algebras: the definition
The Boolean algebras we have seen so far have all been concrete, consisting of bit vectors or equivalently of subsets of some set. Such a Boolean algebra consists of a set and operations on that set which can be shown to satisfy the laws of Boolean algebra.Instead of showing that the Boolean laws are satisfied, we can instead postulate a set X, two binary operations on X, and one unary operation, and require that those operations satisfy the laws of Boolean algebra. The elements of X need not be bit vectors or subsets but can be anything at all. This leads to the more general abstract definition.
- A Boolean algebra is any set with binary operations ∧ and ∨ and a unary operation ¬ thereon satisfying the Boolean laws.[18]
Given any complete axiomatization of Boolean algebra, such as the axioms for a complemented distributive lattice, a sufficient condition for an algebraic structure of this kind to satisfy all the Boolean laws is that it satisfy just those axioms. The following is therefore an equivalent definition.
- A Boolean algebra is a complemented distributive lattice.
Representable Boolean algebras
Although every concrete Boolean algebra is a Boolean algebra, not every Boolean algebra need be concrete. Let n be a square-free positive integer, one not divisible by the square of an integer, for example 30 but not 12. The operations of greatest common divisor, least common multiple, and division into n (that is, ¬x = n/x), can be shown to satisfy all the Boolean laws when their arguments range over the positive divisors of n. Hence those divisors form a Boolean algebra. These divisors are not subsets of a set, making the divisors of n a Boolean algebra that is not concrete according to our definitions.However, if we represent each divisor of n by the set of its prime factors, we find that this nonconcrete Boolean algebra is isomorphic to the concrete Boolean algebra consisting of all sets of prime factors of n, with union corresponding to least common multiple, intersection to greatest common divisor, and complement to division into n. So this example while not technically concrete is at least "morally" concrete via this representation, called an isomorphism. This example is an instance of the following notion.
- A Boolean algebra is called representable when it is isomorphic to a concrete Boolean algebra.
- Every Boolean algebra is representable.
- The laws satisfied by all Boolean algebras coincide with those satisfied by the prototypical Boolean algebra.
Axiomatizing Boolean algebra
The above definition of an abstract Boolean algebra as a set and operations satisfying "the" Boolean laws raises the question, what are those laws? A simple-minded answer is "all Boolean laws," which can be defined as all equations that hold for the Boolean algebra of 0 and 1. Since there are infinitely many such laws this is not a terribly satisfactory answer in practice, leading to the next question: does it suffice to require only finitely many laws to hold?In the case of Boolean algebras the answer is yes. In particular the finitely many equations we have listed above suffice. We say that Boolean algebra is finitely axiomatizable or finitely based.
Can this list be made shorter yet? Again the answer is yes. To begin with, some of the above laws are implied by some of the others. A sufficient subset of the above laws consists of the pairs of associativity, commutativity, and absorption laws, distributivity of ∧ over ∨ (or the other distributivity law—one suffices), and the two complement laws. In fact this is the traditional axiomatization of Boolean algebra as a complemented distributive lattice.
By introducing additional laws not listed above it becomes possible to shorten the list yet further. In 1933 Edward Huntington showed that if the basic operations are taken to be x∨y and ¬x, with x∧y considered a derived operation (e.g. via De Morgan's law in the form x∧y = ¬(¬x∨¬y)), then the equation ¬(¬x∨¬y)∨¬(¬x∨y) = x along with the two equations expressing associativity and commutativity of ∨ completely axiomatized Boolean algebra. When the only basic operation is the binary NAND operation ¬(x∧y), Stephen Wolfram has proposed in his book A New Kind of Science the single axiom (((xy)z)(x((xz)x))) = z as a one-equation axiomatization of Boolean algebra, where for convenience here xy denotes the NAND rather than the AND of x and y.
Propositional logic
Propositional logic is a logical system that is intimately connected to Boolean algebra.[4] Many syntactic concepts of Boolean algebra carry over to propositional logic with only minor changes in notation and terminology, while the semantics of propositional logic are defined via Boolean algebras in a way that the tautologies (theorems) of propositional logic correspond to equational theorems of Boolean algebra.Syntactically, every Boolean term corresponds to a propositional formula of propositional logic. In this translation between Boolean algebra and propositional logic, Boolean variables x,y… become propositional variables (or atoms) P,Q,…, Boolean terms such as x∨y become propositional formulas P∨Q, 0 becomes false or ⊥, and 1 becomes true or T. It is convenient when referring to generic propositions to use Greek letters Φ, Ψ,… as metavariables (variables outside the language of propositional calculus, used when talking about propositional calculus) to denote propositions.
The semantics of propositional logic rely on truth assignments. The essential idea of a truth assignment is that the propositional variables are mapped to elements of a fixed Boolean algebra, and then the truth value of a propositional formula using these letters is the element of the Boolean algebra that is obtained by computing the value of the Boolean term corresponding to the formula. In classical semantics, only the two-element Boolean algebra is used, while in Boolean-valued semantics arbitrary Boolean algebras are considered. A tautology is a propositional formula that is assigned truth value 1 by every truth assignment of its propositional variables to an arbitrary Boolean algebra (or, equivalently, every truth assignment to the two element Boolean algebra).
These semantics permit a translation between tautologies of propositional logic and equational theorems of Boolean algebra. Every tautology Φ of propositional logic can be expressed as the Boolean equation Φ = 1, which will be a theorem of Boolean algebra. Conversely every theorem Φ = Ψ of Boolean algebra corresponds to the tautologies (Φ∨¬Ψ) ∧ (¬Φ∨Ψ) and (Φ∧Ψ) ∨ (¬Φ∧¬Ψ). If → is in the language these last tautologies can also be written as (Φ→Ψ) ∧ (Ψ→Φ), or as two separate theorems Φ→Ψ and Ψ→Φ; if ≡ is available then the single tautology Φ ≡ Ψ can be used.
Applications
One motivating application of propositional calculus is the analysis of propositions and deductive arguments in natural language. Whereas the proposition "if x = 3 then x+1 = 4" depends on the meanings of such symbols as + and 1, the proposition "if x = 3 then x = 3" does not; it is true merely by virtue of its structure, and remains true whether "x = 3" is replaced by "x = 4" or "the moon is made of green cheese." The generic or abstract form of this tautology is "if P then P", or in the language of Boolean algebra, "P → P".Replacing P by x = 3 or any other proposition is called instantiation of P by that proposition. The result of instantiating P in an abstract proposition is called an instance of the proposition. Thus "x = 3 → x = 3" is a tautology by virtue of being an instance of the abstract tautology "P → P". All occurrences of the instantiated variable must be instantiated with the same proposition, to avoid such nonsense as P → x = 3 or x = 3 → x = 4.
Propositional calculus restricts attention to abstract propositions, those built up from propositional variables using Boolean operations. Instantiation is still possible within propositional calculus, but only by instantiating propositional variables by abstract propositions, such as instantiating Q by Q→P in P→(Q→P) to yield the instance P→((Q→P)→P).
(The availability of instantiation as part of the machinery of propositional calculus avoids the need for metavariables within the language of propositional calculus, since ordinary propositional variables can be considered within the language to denote arbitrary propositions. The metavariables themselves are outside the reach of instantiation, not being part of the language of propositional calculus but rather part of the same language for talking about it that this sentence is written in, where we need to be able to distinguish propositional variables and their instantiations as being distinct syntactic entities.)
Deductive systems for propositional logic
An axiomatization of propositional calculus is a set of tautologies called axioms and one or more inference rules for producing new tautologies from old. A proof in an axiom system A is a finite nonempty sequence of propositions each of which is either an instance of an axiom of A or follows by some rule of A from propositions appearing earlier in the proof (thereby disallowing circular reasoning). The last proposition is the theorem proved by the proof. Every nonempty initial segment of a proof is itself a proof, whence every proposition in a proof is itself a theorem. An axiomatization is sound when every theorem is a tautology, and complete when every tautology is a theorem.[19]Sequent calculus
Propositional calculus is commonly organized as a Hilbert system, whose operations are just those of Boolean algebra and whose theorems are Boolean tautologies, those Boolean terms equal to the Boolean constant 1. Another form is sequent calculus, which has two sorts, propositions as in ordinary propositional calculus, and pairs of lists of propositions called sequents, such as A∨B, A∧C,… A, B→C,….
The two halves of a sequent are called the antecedent and the succedent
respectively. The customary metavariable denoting an antecedent or part
thereof is Γ, and for a succedent Δ; thus Γ,A
A, B→C,….
The two halves of a sequent are called the antecedent and the succedent
respectively. The customary metavariable denoting an antecedent or part
thereof is Γ, and for a succedent Δ; thus Γ,A  Δ would denote a sequent whose succedent is a list Δ and whose antecedent is a list Γ with an additional proposition A
appended after it. The antecedent is interpreted as the conjunction of
its propositions, the succedent as the disjunction of its propositions,
and the sequent itself as the entailment of the succedent by the antecedent.
Δ would denote a sequent whose succedent is a list Δ and whose antecedent is a list Γ with an additional proposition A
appended after it. The antecedent is interpreted as the conjunction of
its propositions, the succedent as the disjunction of its propositions,
and the sequent itself as the entailment of the succedent by the antecedent.
Entailment differs from implication in that whereas the latter is a binary operation that returns a value in a Boolean algebra, the former is a binary relation which either holds or does not hold. In this sense entailment is an external form of implication, meaning external to the Boolean algebra, thinking of the reader of the sequent as also being external and interpreting and comparing antecedents and succedents in some Boolean algebra. The natural interpretation of
 is as ≤ in the partial order of the Boolean algebra defined by x ≤ y just when x∨y = y. This ability to mix external implication
is as ≤ in the partial order of the Boolean algebra defined by x ≤ y just when x∨y = y. This ability to mix external implication  and internal implication → in the one logic is among the essential
differences between sequent calculus and propositional calculus.[20]
and internal implication → in the one logic is among the essential
differences between sequent calculus and propositional calculus.[20]
Applications
Boolean algebra as the calculus of two values is fundamental to computer circuits, computer programming, and mathematical logic, and is also used in other areas of mathematics such as set theory and statistics.[4]Computers
In the early 20th century, several electrical engineers intuitively recognized that Boolean algebra was analogous to the behavior of certain types of electrical circuits. Claude Shannon formally proved such behavior was logically equivalent to Boolean algebra in his 1937 master's thesis, A Symbolic Analysis of Relay and Switching Circuits.Today, all modern general purpose computers perform their functions using two-value Boolean logic; that is, their electrical circuits are a physical manifestation of two-value Boolean logic. They achieve this in various ways: as voltages on wires in high-speed circuits and capacitive storage devices, as orientations of a magnetic domain in ferromagnetic storage devices, as holes in punched cards or paper tape, and so on. (Some early computers used decimal circuits or mechanisms instead of two-valued logic circuits.)
Of course, it is possible to code more than two symbols in any given medium. For example, one might use respectively 0, 1, 2, and 3 volts to code a four-symbol alphabet on a wire, or holes of different sizes in a punched card. In practice, the tight constraints of high speed, small size, and low power combine to make noise a major factor. This makes it hard to distinguish between symbols when there are several possible symbols that could occur at a single site. Rather than attempting to distinguish between four voltages on one wire, digital designers have settled on two voltages per wire, high and low.
Computers use two-value Boolean circuits for the above reasons. The most common computer architectures use ordered sequences of Boolean values, called bits, of 32 or 64 values, e.g. 01101000110101100101010101001011. When programming in machine code, assembly language, and certain other programming languages, programmers work with the low-level digital structure of the data registers. These registers operate on voltages, where zero volts represents Boolean 0, and a reference voltage (often +5V, +3.3V, +1.8V) represents Boolean 1. Such languages support both numeric operations and logical operations. In this context, "numeric" means that the computer treats sequences of bits as binary numbers (base two numbers) and executes arithmetic operations like add, subtract, multiply, or divide. "Logical" refers to the Boolean logical operations of disjunction, conjunction, and negation between two sequences of bits, in which each bit in one sequence is simply compared to its counterpart in the other sequence. Programmers therefore have the option of working in and applying the rules of either numeric algebra or Boolean algebra as needed. A core differentiating feature between these families of operations is the existence of the carry operation in the first but not the second.
Two-valued logic
Other areas where two values is a good choice are the law and mathematics. In everyday relaxed conversation, nuanced or complex answers such as "maybe" or "only on the weekend" are acceptable. In more focused situations such as a court of law or theorem-based mathematics however it is deemed advantageous to frame questions so as to admit a simple yes-or-no answer—is the defendant guilty or not guilty, is the proposition true or false—and to disallow any other answer. However much of a straitjacket this might prove in practice for the respondent, the principle of the simple yes-no question has become a central feature of both judicial and mathematical logic, making two-valued logic deserving of organization and study in its own right.A central concept of set theory is membership. Now an organization may permit multiple degrees of membership, such as novice, associate, and full. With sets however an element is either in or out. The candidates for membership in a set work just like the wires in a digital computer: each candidate is either a member or a nonmember, just as each wire is either high or low.
Algebra being a fundamental tool in any area amenable to mathematical treatment, these considerations combine to make the algebra of two values of fundamental importance to computer hardware, mathematical logic, and set theory.
Two-valued logic can be extended to multi-valued logic, notably by replacing the Boolean domain {0, 1} with the unit interval [0,1], in which case rather than only taking values 0 or 1, any value between and including 0 and 1 can be assumed. Algebraically, negation (NOT) is replaced with 1 − x, conjunction (AND) is replaced with multiplication (
 ), and disjunction (OR) is defined via De Morgan's law. Interpreting these values as logical truth values yields a multi-valued logic, which forms the basis for fuzzy logic and probabilistic logic.
In these interpretations, a value is interpreted as the "degree" of
truth – to what extent a proposition is true, or the probability that
the proposition is true.
), and disjunction (OR) is defined via De Morgan's law. Interpreting these values as logical truth values yields a multi-valued logic, which forms the basis for fuzzy logic and probabilistic logic.
In these interpretations, a value is interpreted as the "degree" of
truth – to what extent a proposition is true, or the probability that
the proposition is true.
Boolean operations
The original application for Boolean operations was mathematical logic, where it combines the truth values, true or false, of individual formulas.Natural languages such as English have words for several Boolean operations, in particular conjunction (and), disjunction (or), negation (not), and implication (implies). But not is synonymous with and not. When used to combine situational assertions such as "the block is on the table" and "cats drink milk," which naively are either true or false, the meanings of these logical connectives often have the meaning of their logical counterparts. However, with descriptions of behavior such as "Jim walked through the door", one starts to notice differences such as failure of commutativity, for example the conjunction of "Jim opened the door" with "Jim walked through the door" in that order is not equivalent to their conjunction in the other order, since and usually means and then in such cases. Questions can be similar: the order "Is the sky blue, and why is the sky blue?" makes more sense than the reverse order. Conjunctive commands about behavior are like behavioral assertions, as in get dressed and go to school. Disjunctive commands such love me or leave me or fish or cut bait tend to be asymmetric via the implication that one alternative is less preferable. Conjoined nouns such as tea and milk generally describe aggregation as with set union while tea or milk is a choice. However context can reverse these senses, as in your choices are coffee and tea which usually means the same as your choices are coffee or tea (alternatives). Double negation as in "I don't not like milk" rarely means literally "I do like milk" but rather conveys some sort of hedging, as though to imply that there is a third possibility. "Not not P" can be loosely interpreted as "surely P", and although P necessarily implies "not not P" the converse is suspect in English, much as with intuitionistic logic. In view of the highly idiosyncratic usage of conjunctions in natural languages, Boolean algebra cannot be considered a reliable framework for interpreting them.
Boolean operations are used in digital logic to combine the bits carried on individual wires, thereby interpreting them over {0,1}. When a vector of n identical binary gates are used to combine two bit vectors each of n bits, the individual bit operations can be understood collectively as a single operation on values from a Boolean algebra with 2n elements.
Naive set theory interprets Boolean operations as acting on subsets of a given set X. As we saw earlier this behavior exactly parallels the coordinate-wise combinations of bit vectors, with the union of two sets corresponding to the disjunction of two bit vectors and so on.
The 256-element free Boolean algebra on three generators is deployed in computer displays based on raster graphics, which use bit blit to manipulate whole regions consisting of pixels, relying on Boolean operations to specify how the source region should be combined with the destination, typically with the help of a third region called the mask. Modern video cards offer all 223 = 256 ternary operations for this purpose, with the choice of operation being a one-byte (8-bit) parameter. The constants SRC = 0xaa or 10101010, DST = 0xcc or 11001100, and MSK = 0xf0 or 11110000 allow Boolean operations such as (SRC^DST)&MSK (meaning XOR the source and destination and then AND the result with the mask) to be written directly as a constant denoting a byte calculated at compile time, 0x60 in the (SRC^DST)&MSK example, 0x66 if just SRC^DST, etc. At run time the video card interprets the byte as the raster operation indicated by the original expression in a uniform way that requires remarkably little hardware and which takes time completely independent of the complexity of the expression.
Solid modeling systems for computer aided design offer a variety of methods for building objects from other objects, combination by Boolean operations being one of them. In this method the space in which objects exist is understood as a set S of voxels (the three-dimensional analogue of pixels in two-dimensional graphics) and shapes are defined as subsets of S, allowing objects to be combined as sets via union, intersection, etc. One obvious use is in building a complex shape from simple shapes simply as the union of the latter. Another use is in sculpting understood as removal of material: any grinding, milling, routing, or drilling operation that can be performed with physical machinery on physical materials can be simulated on the computer with the Boolean operation x ∧ ¬y or x − y, which in set theory is set difference, remove the elements of y from those of x. Thus given two shapes one to be machined and the other the material to be removed, the result of machining the former to remove the latter is described simply as their set difference.
Boolean searches
Search engine queries also employ Boolean logic. For this application, each web page on the Internet may be considered to be an "element" of a "set". The following examples use a syntax supported by Google.[21]- Doublequotes are used to combine whitespace-separated words into a single search term.[22]
- Whitespace is used to specify logical AND, as it is the default operator for joining search terms:
"Search term 1" "Search term 2"
- The OR keyword is used for logical OR:
"Search term 1" OR "Search term 2"
- A prefixed minus sign is used for logical NOT:
"Search term 1" −"Search term 2"