Computer science is the study of computation, information, and automation. Computer science spans theoretical disciplines (such as algorithms, theory of computation, and information theory) to applied disciplines (including the design and implementation of hardware and software).
Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of repositories of data. Human–computer interaction investigates the interfaces through which humans and computers interact, and software engineering focuses on the design and principles behind developing software. Areas such as operating systems, networks and embedded systems investigate the principles and design behind complex systems. Computer architecture describes the construction of computer components and computer-operated equipment. Artificial intelligence and machine learning aim to synthesize goal-orientated processes such as problem-solving, decision-making, environmental adaptation, planning and learning found in humans and animals. Within artificial intelligence, computer vision aims to understand and process image and video data, while natural language processing aims to understand and process textual and linguistic data.
The fundamental concern of computer science is determining what can and cannot be automated. The Turing Award is generally recognized as the highest distinction in computer science.
History
| History of computing |
|---|
 |



The earliest foundations of what would become computer science predate the invention of the modern digital computer. Machines for calculating fixed numerical tasks such as the abacus have existed since antiquity, aiding in computations such as multiplication and division. Algorithms for performing computations have existed since antiquity, even before the development of sophisticated computing equipment.
Wilhelm Schickard designed and constructed the first working mechanical calculator in 1623. In 1673, Gottfried Leibniz demonstrated a digital mechanical calculator, called the Stepped Reckoner. Leibniz may be considered the first computer scientist and information theorist, because of various reasons, including the fact that he documented the binary number system. In 1820, Thomas de Colmar launched the mechanical calculator industry when he invented his simplified arithmometer, the first calculating machine strong enough and reliable enough to be used daily in an office environment. Charles Babbage started the design of the first automatic mechanical calculator, his Difference Engine, in 1822, which eventually gave him the idea of the first programmable mechanical calculator, his Analytical Engine. He started developing this machine in 1834, and "in less than two years, he had sketched out many of the salient features of the modern computer". "A crucial step was the adoption of a punched card system derived from the Jacquard loom" making it infinitely programmable. In 1843, during the translation of a French article on the Analytical Engine, Ada Lovelace wrote, in one of the many notes she included, an algorithm to compute the Bernoulli numbers, which is considered to be the first published algorithm ever specifically tailored for implementation on a computer. Around 1885, Herman Hollerith invented the tabulator, which used punched cards to process statistical information; eventually his company became part of IBM. Following Babbage, although unaware of his earlier work, Percy Ludgate in 1909 published the 2nd of the only two designs for mechanical analytical engines in history. In 1914, the Spanish engineer Leonardo Torres Quevedo published his Essays on Automatics, and designed, inspired by Babbage, a theoretical electromechanical calculating machine which was to be controlled by a read-only program. The paper also introduced the idea of floating-point arithmetic. In 1920, to celebrate the 100th anniversary of the invention of the arithmometer, Torres presented in Paris the Electromechanical Arithmometer, a prototype that demonstrated the feasibility of an electromechanical analytical engine, on which commands could be typed and the results printed automatically. In 1937, one hundred years after Babbage's impossible dream, Howard Aiken convinced IBM, which was making all kinds of punched card equipment and was also in the calculator business to develop his giant programmable calculator, the ASCC/Harvard Mark I, based on Babbage's Analytical Engine, which itself used cards and a central computing unit. When the machine was finished, some hailed it as "Babbage's dream come true".
During the 1940s, with the development of new and more powerful computing machines such as the Atanasoff–Berry computer and ENIAC, the term computer came to refer to the machines rather than their human predecessors. As it became clear that computers could be used for more than just mathematical calculations, the field of computer science broadened to study computation in general. In 1945, IBM founded the Watson Scientific Computing Laboratory at Columbia University in New York City. The renovated fraternity house on Manhattan's West Side was IBM's first laboratory devoted to pure science. The lab is the forerunner of IBM's Research Division, which today operates research facilities around the world. Ultimately, the close relationship between IBM and Columbia University was instrumental in the emergence of a new scientific discipline, with Columbia offering one of the first academic-credit courses in computer science in 1946. Computer science began to be established as a distinct academic discipline in the 1950s and early 1960s. The world's first computer science degree program, the Cambridge Diploma in Computer Science, began at the University of Cambridge Computer Laboratory in 1953. The first computer science department in the United States was formed at Purdue University in 1962. Since practical computers became available, many applications of computing have become distinct areas of study in their own rights.
Etymology and scope
Although first proposed in 1956, the term "computer science" appears in a 1959 article in Communications of the ACM, in which Louis Fein argues for the creation of a Graduate School in Computer Sciences analogous to the creation of Harvard Business School in 1921. Louis justifies the name by arguing that, like management science, the subject is applied and interdisciplinary in nature, while having the characteristics typical of an academic discipline. This effort, and those of others such as numerical analyst George Forsythe, were successful, and universities went on to create such departments, starting with Purdue in 1962. Despite its name, a significant amount of computer science does not involve the study of computers themselves. Because of this, several alternative names have been proposed. Certain departments of major universities prefer the term computing science, to emphasize precisely that difference. Danish scientist Peter Naur suggested the term datalogy, to reflect the fact that the scientific discipline revolves around data and data treatment, while not necessarily involving computers. The first scientific institution to use the term was the Department of Datalogy at the University of Copenhagen, founded in 1969, with Peter Naur being the first professor in datalogy. The term is used mainly in the Scandinavian countries. An alternative term, also proposed by Naur, is data science; this is now used for a multi-disciplinary field of data analysis, including statistics and databases.
In the early days of computing, a number of terms for the practitioners of the field of computing were suggested (albeit facetiously) in the Communications of the ACM—turingineer, turologist, flow-charts-man, applied meta-mathematician, and applied epistemologist. Three months later in the same journal, comptologist was suggested, followed next year by hypologist. The term computics has also been suggested. In Europe, terms derived from contracted translations of the expression "automatic information" (e.g. "informazione automatica" in Italian) or "information and mathematics" are often used, e.g. informatique (French), Informatik (German), informatica (Italian, Dutch), informática (Spanish, Portuguese), informatika (Slavic languages and Hungarian) or pliroforiki (πληροφορική, which means informatics) in Greek. Similar words have also been adopted in the UK (as in the School of Informatics, University of Edinburgh). "In the U.S., however, informatics is linked with applied computing, or computing in the context of another domain."
A folkloric quotation, often attributed to—but almost certainly not first formulated by—Edsger Dijkstra, states that "computer science is no more about computers than astronomy is about telescopes." The design and deployment of computers and computer systems is generally considered the province of disciplines other than computer science. For example, the study of computer hardware is usually considered part of computer engineering, while the study of commercial computer systems and their deployment is often called information technology or information systems. However, there has been exchange of ideas between the various computer-related disciplines. Computer science research also often intersects other disciplines, such as cognitive science, linguistics, mathematics, physics, biology, Earth science, statistics, philosophy, and logic.
Computer science is considered by some to have a much closer relationship with mathematics than many scientific disciplines, with some observers saying that computing is a mathematical science. Early computer science was strongly influenced by the work of mathematicians such as Kurt Gödel, Alan Turing, John von Neumann, Rózsa Péter and Alonzo Church and there continues to be a useful interchange of ideas between the two fields in areas such as mathematical logic, category theory, domain theory, and algebra.
The relationship between computer science and software engineering is a contentious issue, which is further muddied by disputes over what the term "software engineering" means, and how computer science is defined. David Parnas, taking a cue from the relationship between other engineering and science disciplines, has claimed that the principal focus of computer science is studying the properties of computation in general, while the principal focus of software engineering is the design of specific computations to achieve practical goals, making the two separate but complementary disciplines.
The academic, political, and funding aspects of computer science tend to depend on whether a department is formed with a mathematical emphasis or with an engineering emphasis. Computer science departments with a mathematics emphasis and with a numerical orientation consider alignment with computational science. Both types of departments tend to make efforts to bridge the field educationally if not across all research.
Philosophy
Epistemology of computer science
Despite the word science in its name, there is debate over whether or not computer science is a discipline of science, mathematics, or engineering. Allen Newell and Herbert A. Simon argued in 1975,
Computer science is an empirical discipline. We would have called it an experimental science, but like astronomy, economics, and geology, some of its unique forms of observation and experience do not fit a narrow stereotype of the experimental method. Nonetheless, they are experiments. Each new machine that is built is an experiment. Actually constructing the machine poses a question to nature; and we listen for the answer by observing the machine in operation and analyzing it by all analytical and measurement means available.
It has since been argued that computer science can be classified as an empirical science since it makes use of empirical testing to evaluate the correctness of programs, but a problem remains in defining the laws and theorems of computer science (if any exist) and defining the nature of experiments in computer science. Proponents of classifying computer science as an engineering discipline argue that the reliability of computational systems is investigated in the same way as bridges in civil engineering and airplanes in aerospace engineering. They also argue that while empirical sciences observe what presently exists, computer science observes what is possible to exist and while scientists discover laws from observation, no proper laws have been found in computer science and it is instead concerned with creating phenomena.
Proponents of classifying computer science as a mathematical discipline argue that computer programs are physical realizations of mathematical entities and programs that can be deductively reasoned through mathematical formal methods. Computer scientists Edsger W. Dijkstra and Tony Hoare regard instructions for computer programs as mathematical sentences and interpret formal semantics for programming languages as mathematical axiomatic systems.
Paradigms of computer science
A number of computer scientists have argued for the distinction of three separate paradigms in computer science. Peter Wegner argued that those paradigms are science, technology, and mathematics. Peter Denning's working group argued that they are theory, abstraction (modeling), and design. Amnon H. Eden described them as the "rationalist paradigm" (which treats computer science as a branch of mathematics, which is prevalent in theoretical computer science, and mainly employs deductive reasoning), the "technocratic paradigm" (which might be found in engineering approaches, most prominently in software engineering), and the "scientific paradigm" (which approaches computer-related artifacts from the empirical perspective of natural sciences, identifiable in some branches of artificial intelligence). Computer science focuses on methods involved in design, specification, programming, verification, implementation and testing of human-made computing systems.
Fields
As a discipline, computer science spans a range of topics from theoretical studies of algorithms and the limits of computation to the practical issues of implementing computing systems in hardware and software. CSAB, formerly called Computing Sciences Accreditation Board—which is made up of representatives of the Association for Computing Machinery (ACM), and the IEEE Computer Society (IEEE CS)—identifies four areas that it considers crucial to the discipline of computer science: theory of computation, algorithms and data structures, programming methodology and languages, and computer elements and architecture. In addition to these four areas, CSAB also identifies fields such as software engineering, artificial intelligence, computer networking and communication, database systems, parallel computation, distributed computation, human–computer interaction, computer graphics, operating systems, and numerical and symbolic computation as being important areas of computer science.
Theoretical computer science
Theoretical computer science is mathematical and abstract in spirit, but it derives its motivation from practical and everyday computation. It aims to understand the nature of computation and, as a consequence of this understanding, provide more efficient methodologies.
Theory of computation
According to Peter Denning, the fundamental question underlying computer science is, "What can be automated?" Theory of computation is focused on answering fundamental questions about what can be computed and what amount of resources are required to perform those computations. In an effort to answer the first question, computability theory examines which computational problems are solvable on various theoretical models of computation. The second question is addressed by computational complexity theory, which studies the time and space costs associated with different approaches to solving a multitude of computational problems.
The famous P = NP? problem, one of the Millennium Prize Problems, is an open problem in the theory of computation.
|

|

| |
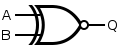
| Automata theory | Formal languages | Computability theory | Computational complexity theory |

|
|
|

|
| Models of computation | Quantum computing theory | Logic circuit theory | Cellular automata |
Information and coding theory
Information theory, closely related to probability and statistics, is related to the quantification of information. This was developed by Claude Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and communicating data. Coding theory is the study of the properties of codes (systems for converting information from one form to another) and their fitness for a specific application. Codes are used for data compression, cryptography, error detection and correction, and more recently also for network coding. Codes are studied for the purpose of designing efficient and reliable data transmission methods.

|

|

|

|

|
| Coding theory | Channel capacity | Algorithmic information theory | Signal detection theory | Kolmogorov complexity |
Data structures and algorithms
Data structures and algorithms are the studies of commonly used computational methods and their computational efficiency.
| O(n2) | 
|

|
|

|

|
| Analysis of algorithms | Algorithm design | Data structures | Combinatorial optimization | Computational geometry | Randomized algorithms |
Programming language theory and formal methods
Programming language theory is a branch of computer science that deals with the design, implementation, analysis, characterization, and classification of programming languages and their individual features. It falls within the discipline of computer science, both depending on and affecting mathematics, software engineering, and linguistics. It is an active research area, with numerous dedicated academic journals.
Formal methods are a particular kind of mathematically based technique for the specification, development and verification of software and hardware systems. The use of formal methods for software and hardware design is motivated by the expectation that, as in other engineering disciplines, performing appropriate mathematical analysis can contribute to the reliability and robustness of a design. They form an important theoretical underpinning for software engineering, especially where safety or security is involved. Formal methods are a useful adjunct to software testing since they help avoid errors and can also give a framework for testing. For industrial use, tool support is required. However, the high cost of using formal methods means that they are usually only used in the development of high-integrity and life-critical systems, where safety or security is of utmost importance. Formal methods are best described as the application of a fairly broad variety of theoretical computer science fundamentals, in particular logic calculi, formal languages, automata theory, and program semantics, but also type systems and algebraic data types to problems in software and hardware specification and verification.

|

|

|

|

| |
| Formal semantics | Type theory | Compiler design | Programming languages | Formal verification | Automated theorem proving |
Applied computer science
Computer graphics and visualization
Computer graphics is the study of digital visual contents and involves the synthesis and manipulation of image data. The study is connected to many other fields in computer science, including computer vision, image processing, and computational geometry, and is heavily applied in the fields of special effects and video games.

|

|

|

|

| |
| 2D computer graphics | Computer animation | Rendering | Mixed reality | Virtual reality | Solid modeling |
Image and sound processing
Information can take the form of images, sound, video or other multimedia. Bits of information can be streamed via signals. Its processing is the central notion of informatics, the European view on computing, which studies information processing algorithms independently of the type of information carrier – whether it is electrical, mechanical or biological. This field plays important role in information theory, telecommunications, information engineering and has applications in medical image computing and speech synthesis, among others. What is the lower bound on the complexity of fast Fourier transform algorithms? is one of the unsolved problems in theoretical computer science.

|

|

|

|

|

|
| FFT algorithms | Image processing | Speech recognition | Data compression | Medical image computing | Speech synthesis |
Computational science, finance and engineering
Scientific computing (or computational science) is the field of study concerned with constructing mathematical models and quantitative analysis techniques and using computers to analyze and solve scientific problems. A major usage of scientific computing is simulation of various processes, including computational fluid dynamics, physical, electrical, and electronic systems and circuits, societies and social situations (notably war games) along with their habitats, and interactions among biological cells. Modern computers enable optimization of such designs as complete aircraft. Notable in electrical and electronic circuit design are SPICE, as well as software for physical realization of new (or modified) designs. The latter includes essential design software for integrated circuits.

|

|
|
|
|

|

|

|

|
| Numerical analysis | Computational physics | Computational chemistry | Bioinformatics | Neuroinformatics | Psychoinformatics | Medical informatics | Computational engineering | Computational musicology |
Human–computer interaction
Human–computer interaction (HCI) is the field of study and research concerned with the design and use of computer systems, mainly based on the analysis of the interaction between humans and computer interfaces. HCI has several subfields that focus on the relationship between emotions, social behavior and brain activity with computers.

|

|

| ||
| Affective computing | Brain–computer interface | Human-centered design | Physical computing | Social computing |
Software engineering
Software engineering is the study of designing, implementing, and modifying the software in order to ensure it is of high quality, affordable, maintainable, and fast to build. It is a systematic approach to software design, involving the application of engineering practices to software. Software engineering deals with the organizing and analyzing of software—it does not just deal with the creation or manufacture of new software, but its internal arrangement and maintenance. For example software testing, systems engineering, technical debt and software development processes.
Artificial intelligence
Artificial intelligence (AI) aims to or is required to synthesize goal-orientated processes such as problem-solving, decision-making, environmental adaptation, learning, and communication found in humans and animals. From its origins in cybernetics and in the Dartmouth Conference (1956), artificial intelligence research has been necessarily cross-disciplinary, drawing on areas of expertise such as applied mathematics, symbolic logic, semiotics, electrical engineering, philosophy of mind, neurophysiology, and social intelligence. AI is associated in the popular mind with robotic development, but the main field of practical application has been as an embedded component in areas of software development, which require computational understanding. The starting point in the late 1940s was Alan Turing's question "Can computers think?", and the question remains effectively unanswered, although the Turing test is still used to assess computer output on the scale of human intelligence. But the automation of evaluative and predictive tasks has been increasingly successful as a substitute for human monitoring and intervention in domains of computer application involving complex real-world data.
Computer systems
Computer architecture and microarchitecture
Computer architecture, or digital computer organization, is the conceptual design and fundamental operational structure of a computer system. It focuses largely on the way by which the central processing unit performs internally and accesses addresses in memory. Computer engineers study computational logic and design of computer hardware, from individual processor components, microcontrollers, personal computers to supercomputers and embedded systems. The term "architecture" in computer literature can be traced to the work of Lyle R. Johnson and Frederick P. Brooks Jr., members of the Machine Organization department in IBM's main research center in 1959.
Concurrent, parallel and distributed computing
Concurrency is a property of systems in which several computations are executing simultaneously, and potentially interacting with each other. A number of mathematical models have been developed for general concurrent computation including Petri nets, process calculi and the parallel random access machine model. When multiple computers are connected in a network while using concurrency, this is known as a distributed system. Computers within that distributed system have their own private memory, and information can be exchanged to achieve common goals.
Computer networks
This branch of computer science aims studies the construction and behavior of computer networks. It addresses their performance, resilience, security, scalability, and cost-effectiveness, along with the variety of services they can provide.
Computer security and cryptography
Computer security is a branch of computer technology with the objective of protecting information from unauthorized access, disruption, or modification while maintaining the accessibility and usability of the system for its intended users.
Historical cryptography is the art of writing and deciphering secret messages. Modern cryptography is the scientific study of problems relating to distributed computations that can be attacked. Technologies studied in modern cryptography include symmetric and asymmetric encryption, digital signatures, cryptographic hash functions, key-agreement protocols, blockchain, zero-knowledge proofs, and garbled circuits.
Databases and data mining
A database is intended to organize, store, and retrieve large amounts of data easily. Digital databases are managed using database management systems to store, create, maintain, and search data, through database models and query languages. Data mining is a process of discovering patterns in large data sets.
Discoveries
The philosopher of computing Bill Rapaport noted three Great Insights of Computer Science:
- Gottfried Wilhelm Leibniz's, George Boole's, Alan Turing's, Claude Shannon's, and Samuel Morse's insight: there are only two objects that a computer has to deal with in order to represent "anything".
- All the information about any computable problem can be represented using only 0 and 1 (or any other bistable pair that can flip-flop between two easily distinguishable states, such as "on/off", "magnetized/de-magnetized", "high-voltage/low-voltage", etc.).
- Alan Turing's insight: there are only five actions that a computer has to perform in order to do "anything".
- Every algorithm can be expressed in a language for a computer consisting of only five basic instructions:
- move left one location;
- move right one location;
- read symbol at current location;
- print 0 at current location;
- print 1 at current location.
- Every algorithm can be expressed in a language for a computer consisting of only five basic instructions:
- Corrado Böhm and Giuseppe Jacopini's insight: there are only three ways of combining these actions (into more complex ones) that are needed in order for a computer to do "anything".
- Only three rules are needed to combine any set of basic instructions into more complex ones:
- sequence: first do this, then do that;
- selection: IF such-and-such is the case, THEN do this, ELSE do that;
- repetition: WHILE such-and-such is the case, DO this.
- The three rules of Boehm's and Jacopini's insight can be further simplified with the use of goto (which means it is more elementary than structured programming).
- Only three rules are needed to combine any set of basic instructions into more complex ones:
Programming paradigms
Programming languages can be used to accomplish different tasks in different ways. Common programming paradigms include:
- Functional programming, a style of building the structure and elements of computer programs that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It is a declarative programming paradigm, which means programming is done with expressions or declarations instead of statements.
- Imperative programming, a programming paradigm that uses statements that change a program's state. In much the same way that the imperative mood in natural languages expresses commands, an imperative program consists of commands for the computer to perform. Imperative programming focuses on describing how a program operates.
- Object-oriented programming, a programming paradigm based on the concept of "objects", which may contain data, in the form of fields, often known as attributes; and code, in the form of procedures, often known as methods. A feature of objects is that an object's procedures can access and often modify the data fields of the object with which they are associated. Thus object-oriented computer programs are made out of objects that interact with one another.
- Service-oriented programming, a programming paradigm that uses "services" as the unit of computer work, to design and implement integrated business applications and mission critical software programs.
Many languages offer support for multiple paradigms, making the distinction more a matter of style than of technical capabilities.
Research
Conferences are important events for computer science research. During these conferences, researchers from the public and private sectors present their recent work and meet. Unlike in most other academic fields, in computer science, the prestige of conference papers is greater than that of journal publications. One proposed explanation for this is the quick development of this relatively new field requires rapid review and distribution of results, a task better handled by conferences than by journals.