Chemical equilibrium

From Wikipedia, the free encyclopedia   

In a chemical reaction, chemical equilibrium is the state in which both reactants and products are present in concentrations which have no further tendency to change with time.^[1] Usually, this state results when the forward reaction proceeds at the same rate as the reverse reaction. The reaction rates of the forward and backward reactions are generally not zero, but equal. Thus, there are no net changes in the concentrations of the reactant(s) and product(s). Such a state is known as dynamic equilibrium.^[2][3]

Historical introduction

Burette, a common laboratory apparatus for carrying out titration, an important experimental technique in equilibrium and analytical chemistry.

The concept of chemical equilibrium was developed after Berthollet (1803) found that some chemical reactions are reversible. For any reaction mixture to exist at equilibrium, the rates of the forward and backward (reverse) reactions are equal. In the following chemical equation with arrows pointing both ways to indicate equilibrium, A and B are reactant chemical species, S and T are product species, and α, β, σ, and τ are the stoichiometric coefficients of the respective reactants and products:

The equilibrium position of a reaction is said to lie "far to the right" if, at equilibrium, nearly all the reactants are consumed. Conversely the equilibrium position is said to be "far to the left" if hardly any product is formed from the reactants.

Guldberg and Waage (1865), building on Berthollet’s ideas, proposed the law of mass action:

where A, B, S and T are active masses and k₊ and k₋ are rate constants. Since at equilibrium forward and backward rates are equal:

and the ratio of the rate constants is also a constant, now known as an equilibrium constant.

By convention the products form the numerator. However, the law of mass action is valid only for concerted one-step reactions that proceed through a single transition state and is not valid in general because rate equations do not, in general, follow the stoichiometry of the reaction as Guldberg and Waage had proposed (see, for example, nucleophilic aliphatic substitution by S_N1 or reaction of hydrogen and bromine to form hydrogen bromide). Equality of forward and backward reaction rates, however, is a necessary condition for chemical equilibrium, though it is not sufficient to explain why equilibrium occurs.

Despite the failure of this derivation, the equilibrium constant for a reaction is indeed a constant, independent of the activities of the various species involved, though it does depend on temperature as observed by the van 't Hoff equation. Adding a catalyst will affect both the forward reaction and the reverse reaction in the same way and will not have an effect on the equilibrium constant. The catalyst will speed up both reactions thereby increasing the speed at which equilibrium is reached.^[2][4]
Although the macroscopic equilibrium concentrations are constant in time, reactions do occur at the molecular level. For example, in the case of acetic acid dissolved in water and forming acetate and hydronium ions,

CH₃CO₂H + H₂O ⇌ CH₃CO₂⁻ + H₃O⁺

a proton may hop from one molecule of acetic acid on to a water molecule and then on to an acetate anion to form another molecule of acetic acid and leaving the number of acetic acid molecules unchanged. This is an example of dynamic equilibrium. Equilibria, like the rest of thermodynamics, are statistical phenomena, averages of microscopic behavior.

Le Chatelier's principle (1884) gives an idea of the behavior of an equilibrium system when changes to its reaction conditions occur. If a dynamic equilibrium is disturbed by changing the conditions, the position of equilibrium moves to partially reverse the change. For example, adding more S from the outside will cause an excess of products, and the system will try to counteract this by increasing the reverse reaction and pushing the equilibrium point backward (though the equilibrium constant will stay the same).

If mineral acid is added to the acetic acid mixture, increasing the concentration of hydronium ion, the amount of dissociation must decrease as the reaction is driven to the left in accordance with this principle. This can also be deduced from the equilibrium constant expression for the reaction:

If {H₃O⁺} increases {CH₃CO₂H} must increase and {CH₃CO₂⁻} must decrease. The H₂O is left out as it is a pure liquid and its concentration is undefined.

A quantitative version is given by the reaction quotient.

J. W. Gibbs suggested in 1873 that equilibrium is attained when the Gibbs free energy of the system is at its minimum value (assuming the reaction is carried out at constant temperature and pressure).
What this means is that the derivative of the Gibbs energy with respect to reaction coordinate (a measure of the extent of reaction that has occurred, ranging from zero for all reactants to a maximum for all products) vanishes, signalling a stationary point. This derivative is called the reaction Gibbs energy (or energy change) and corresponds to the difference between the chemical potentials of reactants and products at the composition of the reaction mixture.^[1] This criterion is both necessary and sufficient. If a mixture is not at equilibrium, the liberation of the excess Gibbs energy (or Helmholtz energy at constant volume reactions) is the “driving force” for the composition of the mixture to change until equilibrium is reached. The equilibrium constant can be related to the standard Gibbs free energy change for the reaction by the equation

where R is the universal gas constant and T the temperature.

When the reactants are dissolved in a medium of high ionic strength the quotient of activity coefficients may be taken to be constant. In that case the concentration quotient, K_c,

where [A] is the concentration of A, etc., is independent of the analytical concentration of the reactants. For this reason, equilibrium constants for solutions are usually determined in media of high ionic strength. K_c varies with ionic strength, temperature and pressure (or volume). Likewise K_p for gases depends on partial pressure. These constants are easier to measure and encountered in high-school chemistry courses.

Thermodynamics

At constant temperature and pressure, one must consider the Gibbs free energy, G, while at constant temperature and volume, one must consider the Helmholtz free energy: A, for the reaction; and at constant internal energy and volume, one must consider the entropy for the reaction: S.

The constant volume case is important in geochemistry and atmospheric chemistry where pressure variations are significant. Note that, if reactants and products were in standard state (completely pure), then there would be no reversibility and no equilibrium. The mixing of the products and reactants contributes a large entropy (known as entropy of mixing) to states containing equal mixture of products and reactants. The combination of the standard Gibbs energy change and the Gibbs energy of mixing determines the equilibrium state.^[5][6]

In this article only the constant pressure case is considered. The relation between the Gibbs free energy and the equilibrium constant can be found by considering chemical potentials.^[1]

At constant temperature and pressure, the Gibbs free energy, G, for the reaction depends only on the extent of reaction: ξ (Greek letter xi), and can only decrease according to the second law of thermodynamics. It means that the derivative of G with ξ must be negative if the reaction happens; at the equilibrium the derivative being equal to zero.

: equilibrium

In general an equilibrium system is defined by writing an equilibrium equation for the reaction

In order to meet the thermodynamic condition for equilibrium, the Gibbs energy must be stationary, meaning that the derivative of G with respect to the extent of reaction: ξ, must be zero. It can be shown that in this case, the sum of chemical potentials of the products is equal to the sum of those corresponding to the reactants. Therefore, the sum of the Gibbs energies of the reactants must be the equal to the sum of the Gibbs energies of the products.

where μ is in this case a partial molar Gibbs energy, a chemical potential. The chemical potential of a reagent A is a function of the activity, {A} of that reagent.

, ( is the standard chemical potential ).

Substituting expressions like this into the Gibbs energy equation:

in the case of a closed system.

Now

( corresponds to the Stoichiometric coefficient and is the differential of the extent of reaction ).

At constant pressure and temperature we obtain:

which corresponds to the Gibbs free energy change for the reaction .

This results in:

.

By substituting the chemical potentials:

,

the relationship becomes:

: which is the standard Gibbs energy change for the reaction. It is a constant at a given temperature, which can be calculated, using thermodynamical tables.

( is the reaction quotient when the system is not at equilibrium ).

Therefore

At equilibrium

 ; the reaction quotient becomes equal to the equilibrium constant.

leading to:

and

Obtaining the value of the standard Gibbs energy change, allows the calculation of the equilibrium constant

Addition of reactants or products

For a reactional system at equilibrium: ; .

If are modified activities of constituents, the value of the reaction quotient changes and becomes different from the equilibrium constant:

and

then

• If activity of a reagent increases

, the reaction quotient decreases.

then

and  : The reaction will shift to the right (i.e. in the forward direction, and thus more products will form).

• If activity of a product increases

then

and  : The reaction will shift to the left (i.e. in the reverse direction, and thus less products will form).
Note that activities and equilibrium constants are dimensionless numbers.

Treatment of activity

The expression for the equilibrium constant can be rewritten as the product of a concentration quotient, K_c and an activity coefficient quotient, Γ.

[A] is the concentration of reagent A, etc. It is possible in principle to obtain values of the activity coefficients, γ. For solutions, equations such as the Debye–Hückel equation or extensions such as Davies equation^[7] Specific ion interaction theory or Pitzer equations^[8] may be used.^{Software (below)}. However this is not always possible. It is common practice to assume that Γ is a constant, and to use the concentration quotient in place of the thermodynamic equilibrium constant. It is also general practice to use the term equilibrium constant instead of the more accurate concentration quotient.
This practice will be followed here.

For reactions in the gas phase partial pressure is used in place of concentration and fugacity coefficient in place of activity coefficient. In the real world, for example, when making ammonia in industry, fugacity coefficients must be taken into account. Fugacity, f, is the product of partial pressure and fugacity coefficient. The chemical potential of a species in the gas phase is given by

so the general expression defining an equilibrium constant is valid for both solution and gas phases.

Concentration quotients

In aqueous solution, equilibrium constants are usually determined in the presence of an "inert" electrolyte such as sodium nitrate NaNO₃ or potassium perchlorate KClO₄. The ionic strength of a solution is given by

where c_i and z_i stands for the concentration and ionic charge of ion type i, and the sum is taken over all the N types of charged species in solution. When the concentration of dissolved salt is much higher than the analytical concentrations of the reagents, the ions originating from the dissolved salt determine the ionic strength, and the ionic strength is effectively constant. Since activity coefficients depend on ionic strength the activity coefficients of the species are effectively independent of concentration. Thus, the assumption that Γ is constant is justified. The concentration quotient is a simple multiple of the equilibrium constant.^[9]

However, K_c will vary with ionic strength. If it is measured at a series of different ionic strengths the value can be extrapolated to zero ionic strength.^[8] The concentration quotient obtained in this manner is known, paradoxically, as a thermodynamic equilibrium constant.

To use a published value of an equilibrium constant in conditions of ionic strength different from the conditions used in its determination, the value should be adjusted^{Software (below)}.

Metastable mixtures

A mixture may be appear to have no tendency to change, though it is not at equilibrium. For example, a mixture of SO₂ and O₂ is metastable as there is a kinetic barrier to formation of the product, SO₃.

2SO₂ + O₂ 2SO₃

The barrier can be overcome when a catalyst is also present in the mixture as in the contact process, but the catalyst does not affect the equilibrium concentrations.

Likewise, the formation of bicarbonate from carbon dioxide and water is very slow under normal conditions

CO₂ + 2H₂O HCO₃^- +H₃O⁺

but almost instantaneous in the presence of the catalytic enzyme carbonic anhydrase.

Pure substances

When pure substances (liquids or solids) are involved in equilibria their activities do not appear in the equilibrium constant^[10] because their numerical values are considered one.

Applying the general formula for an equilibrium constant to the specific case of acetic acid one obtains

CH₃CO₂H + H₂O ⇌ CH₃CO₂⁻ + H₃O⁺

It may be assumed that the concentration of water is constant. This assumption will be valid for all but very concentrated solutions. The equilibrium constant expression is therefore usually written as

where now



a constant factor is incorporated into the equilibrium constant.

A particular case is the self-ionization of water itself

The self-ionization constant of water is defined as



It is perfectly legitimate to write [H⁺] for the hydronium ion concentration, since the state of solvation of the proton is constant (in dilute solutions) and so does not affect the equilibrium concentrations. K_w varies with variation in ionic strength and/or temperature.

The concentrations of H⁺ and OH^- are not independent quantities. Most commonly [OH^-] is replaced by K_w[H⁺]⁻¹ in equilibrium constant expressions which would otherwise include hydroxide ion.

Solids also do not appear in the equilibrium constant expression, if they are considered to be pure and thus their activities taken to be one. An example is the Boudouard reaction:^[10]

for which the equation (without solid carbon) is written as:

Multiple equilibria

Consider the case of a dibasic acid H₂A. When dissolved in water, the mixture will contain H₂A, HA^- and A^2-. This equilibrium can be split into two steps in each of which one proton is liberated.

K₁ and K₂ are examples of stepwise equilibrium constants. The overall equilibrium constant,, is product of the stepwise constants.

Note that these constants are dissociation constants because the products on the right hand side of the equilibrium expression are dissociation products. In many systems, it is preferable to use association constants.

β₁ and β₂ are examples of association constants. Clearly β₁ = 1/K₂ and β₂ = 1/β_D; lg β₁ = pK₂ and lg β₂ = pK₂ + pK₁^[11] For multiple equilibrium systems, also see: theory of Response reactions.

Effect of temperature

The effect of changing temperature on an equilibrium constant is given by the van 't Hoff equation

Thus, for exothermic reactions, (ΔH is negative) K decreases with an increase in temperature, but, for endothermic reactions, (ΔH is positive) K increases with an increase temperature. An alternative formulation is

At first sight this appears to offer a means of obtaining the standard molar enthalpy of the reaction by studying the variation of K with temperature. In practice, however, the method is unreliable because error propagation almost always gives very large errors on the values calculated in this way.

Effect of electric and magnetic fields

The effect of electric field on equilibrium has been studied by Manfred Eigen^{[citation needed]} among others.

Types of equilibrium

1. In the gas phase. Rocket engines^[12]
2. The industrial synthesis such as ammonia in the Haber–Bosch process (depicted right) takes place through a succession of equilibrium steps including adsorption processes.
   

   

   Haber–Bosch process
3. atmospheric chemistry
4. Seawater and other natural waters: Chemical oceanography
5. Distribution between two phases
   1. LogD-Distribution coefficient: Important for pharmaceuticals where lipophilicity is a significant property of a drug
   2. Liquid–liquid extraction, Ion exchange, Chromatography
   3. Solubility product
   4. Uptake and release of oxygen by haemoglobin in blood
6. Acid/base equilibria: Acid dissociation constant, hydrolysis, buffer solutions, indicators, acid–base homeostasis
7. Metal-ligand complexation: sequestering agents, chelation therapy, MRI contrast reagents, Schlenk equilibrium
8. Adduct formation: Host–guest chemistry, supramolecular chemistry, molecular recognition, dinitrogen tetroxide
9. In certain oscillating reactions, the approach to equilibrium is not asymptotically but in the form of a damped oscillation .^[10]
10. The related Nernst equation in electrochemistry gives the difference in electrode potential as a function of redox concentrations.
11. When molecules on each side of the equilibrium are able to further react irreversibly in secondary reactions, the final product ratio is determined according to the Curtin–Hammett principle.

In these applications, terms such as stability constant, formation constant, binding constant, affinity constant, association/dissociation constant are used. In biochemistry, it is common to give units for binding constants, which serve to define the concentration units used when the constant’s value was determined.

Composition of a mixture

When the only equilibrium is that of the formation of a 1:1 adduct as the composition of a mixture, there are any number of ways that the composition of a mixture can be calculated. For example, see ICE table for a traditional method of calculating the pH of a solution of a weak acid.

There are three approaches to the general calculation of the composition of a mixture at equilibrium.

1. The most basic approach is to manipulate the various equilibrium constants until the desired concentrations are expressed in terms of measured equilibrium constants (equivalent to measuring chemical potentials) and initial conditions.
2. Minimize the Gibbs energy of the system.^[13]
3. Satisfy the equation of mass balance. The equations of mass balance are simply statements that demonstrate that the total concentration of each reactant must be constant by the law of conservation of mass.

Mass-balance equations

In general, the calculations are rather complicated or complex. For instance, in the case of a dibasic acid, H₂A dissolved in water the two reactants can be specified as the conjugate base, A^2-, and the proton, H⁺. The following equations of mass-balance could apply equally well to a base such as 1,2-diaminoethane, in which case the base itself is designated as the reactant A:

With T_A the total concentration of species A. Note that it is customary to omit the ionic charges when writing and using these equations.

When the equilibrium constants are known and the total concentrations are specified there are two equations in two unknown "free concentrations" [A] and [H]. This follows from the fact that [HA]= β₁[A][H], [H₂A]= β₂[A][H]² and [OH] = K_w[H]⁻¹

so the concentrations of the "complexes" are calculated from the free concentrations and the equilibrium constants. General expressions applicable to all systems with two reagents, A and B would be

It is easy to see how this can be extended to three or more reagents.

Polybasic acids

Species concentrations during hydrolysis of the aluminium.

The composition of solutions containing reactants A and H is easy to calculate as a function of p[H]. When [H] is known, the free concentration [A] is calculated from the mass-balance equation in A.

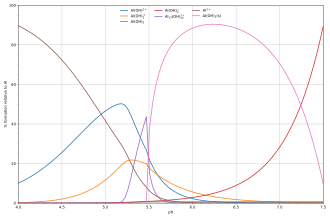
The diagram alongside, shows an example of the hydrolysis of the aluminium Lewis acid Al³⁺_aq^[14] shows the species concentrations for a 5×10⁻⁶M solution of an aluminium salt as a function of pH. Each concentration is shown as a percentage of the total aluminium.

Solution and precipitation

The diagram above illustrates the point that a precipitate that is not one of the main species in the solution equilibrium may be formed. At pH just below 5.5 the main species present in a 5μM solution of Al³⁺ are aluminium hydroxides Al(OH)²⁺, Al(OH)₂⁺ and Al₁₃(OH)₃₂⁷⁺, but on raising the pH Al(OH)₃ precipitates from the solution. This occurs because Al(OH)₃ has a very large lattice energy. As the pH rises more and more Al(OH)₃ comes out of solution. This is an example of Le Chatelier's principle in action: Increasing the concentration of the hydroxide ion causes more aluminium hydroxide to precipitate, which removes hydroxide from the solution. When the hydroxide concentration becomes sufficiently high the soluble aluminate, Al(OH)₄^-, is formed.

Another common instance where precipitation occurs is when a metal cation interacts with an anionic ligand to form an electrically neutral complex. If the complex is hydrophobic, it will precipitate out of water. This occurs with the nickel ion Ni²⁺ and dimethylglyoxime, (dmgH₂): in this case the lattice energy of the solid is not particularly large, but it greatly exceeds the energy of solvation of the molecule Ni(dmgH)₂.

Minimization of free energy

At equilibrium, G is at a minimum:

For a closed system, no particles may enter or leave, although they may combine in various ways.
The total number of atoms of each element will remain constant. This means that the minimization above must be subjected to the constraints:

where is the number of atoms of element i in molecule j and b_i⁰ is the total number of atoms of element i, which is a constant, since the system is closed. If there are a total of k types of atoms in the system, then there will be k such equations.

This is a standard problem in optimisation, known as constrained minimisation. The most common method of solving it is using the method of Lagrange multipliers, also known as undetermined multipliers (though other methods may be used).

Define:

where the are the Lagrange multipliers, one for each element. This allows each of the to be treated independently, and it can be shown using the tools of multivariate calculus that the equilibrium condition is given by

    and    

(For proof see Lagrange multipliers)

This is a set of (m+k) equations in (m+k) unknowns (the and the ) and may, therefore, be solved for the equilibrium concentrations as long as the chemical potentials are known as functions of the concentrations at the given temperature and pressure. (See Thermodynamic databases for pure substances).

This method of calculating equilibrium chemical concentrations is useful for systems with a large number of different molecules. The use of k atomic element conservation equations for the mass constraint is straightforward, and replaces the use of the stoichiometric coefficient equations.^[12]

Entropy

Introduction to entropy

From Wikipedia, the free encyclopedia

 

The idea of "irreversibility" is central to the understanding of entropy. Everyone has an intuitive understanding of irreversibility (a dissipative process) - if one watches a movie of everyday life running forward and in reverse, it is easy to distinguish between the two. The movie running in reverse shows impossible things happening - water jumping out of a glass into a pitcher above it, smoke going down a chimney, water "unmelting" to form ice in a warm room, crashed cars reassembling themselves, and so on. The intuitive meaning of expressions such as "you can't unscramble an egg", "don't cry over spilled milk" or "you can't take the cream out of the coffee" is that these are irreversible processes. There is a direction in time by which spilled milk does not go back into the glass.

In thermodynamics, one says that the "forward" processes – pouring water from a pitcher, smoke going up a chimney, etc. – are "irreversible": they cannot happen in reverse, even though, on a microscopic level, no laws of physics would be violated if they did. All real physical processes involving systems in everyday life, with many atoms or molecules, are irreversible. For an irreversible process in an isolated system, the thermodynamic state variable known as entropy is always increasing. The reason that the movie in reverse is so easily recognized is because it shows processes for which entropy is decreasing, which is physically impossible. In everyday life, there may be processes in which the increase of entropy is practically unobservable, almost zero. In these cases, a movie of the process run in reverse will not seem unlikely. For example, in a 1-second video of the collision of two billiard balls, it will be hard to distinguish the forward and the backward case, because the increase of entropy during that time is relatively small. In thermodynamics, one says that this process is practically "reversible", with an entropy increase that is practically zero. The statement of the fact that entropy never decreases is found in the second law of thermodynamics.

In a physical system, entropy provides a measure of the amount of thermal energy that cannot be used to do work. In some other definitions of entropy, it is a measure of how evenly energy (or some analogous property) is distributed in a system. Work and heat are determined by a process that a system undergoes, and only occur at the boundary of a system. Entropy is a function of the state of a system, and has a value determined by the state variables of the system.

The concept of entropy is central to the second law of thermodynamics. The second law determines which physical processes can occur. For example, it predicts that the flow of heat from a region of high temperature to a region of low temperature is a spontaneous process – it can proceed along by itself without needing any extra external energy. When this process occurs, the hot region becomes cooler and the cold region becomes warmer. Heat is distributed more evenly throughout the system and the system's ability to do work has decreased because the temperature difference between the hot region and the cold region has decreased. Referring back to our definition of entropy, we can see that the entropy of this system has increased. Thus, the second law of thermodynamics can be stated to say that the entropy of an isolated system always increases, and such processes which increase entropy can occur spontaneously. Since entropy increases as uniformity increases, the second law says qualitatively that uniformity increases.

The term entropy was coined in 1865 by the German physicist Rudolf Clausius, from the Greek words en-, "in", and trope "a turning", in analogy with energy.^[1]

Explanation

The concept of thermodynamic entropy arises from the second law of thermodynamics. It uses entropy to quantify the capacity of a system for change, namely that heat flows from a region of higher temperature to one with lower temperature, and to determine whether a thermodynamic process may occur.

Entropy is defined by two descriptions, first as a macroscopic relationship between heat flow into a system and the system's change in temperature, and second, on a microscopic level, as the natural logarithm of the number of microstates of a system.

Following the formalism of Clausius, the first definition can be mathematically stated as:^[2]

Where dS is the change in entropy, δq is the heat added to the system, which holds only during a reversible process^[why?], and T is temperature. If the temperature is allowed to vary, the equation must be integrated over the temperature path. This definition of entropy does not allow the determination of an absolute value, only of differences. In this context, the Second Law of Thermodynamics may be stated that for heat transferred over any valid process for any system, whether isolated or not,

The second definition of entropy comes from statistical mechanics. The entropy of a particular macrostate is defined to be Boltzmann's constant times the natural logarithm of the number of microstates corresponding to that macrostate, or mathematically

Where S is the entropy, k_B is Boltzmann's constant, and Ω is the number of microstates.

The macrostate of a system is what we know about the system, for example the temperature, pressure, and volume of a gas in a box. For each set of values of temperature, pressure, and volume there are many arrangements of molecules which result in those values. The number of arrangements of molecules which could result in the same values for temperature, pressure and volume is the number of microstates.

The concept of energy is related to the first law of thermodynamics, which deals with the conservation of energy and under which the loss in heat will result in a decrease in the internal energy of the thermodynamic system. Thermodynamic entropy provides a comparative measure of the amount of this decrease in internal energy of the system and the corresponding increase in internal energy of the surroundings at a given temperature. A simple and more concrete visualization of the second law is that energy of all types changes from being localized to becoming dispersed or spread out, if it is not hindered from doing so. Entropy change is the quantitative measure of that kind of a spontaneous process: how much energy has flowed or how widely it has become spread out at a specific temperature.

Entropy has been developed to describe any of several phenomena, depending on the field and the context in which it is being used. Information entropy takes the mathematical concepts of statistical thermodynamics into areas of probability theory unconnected with heat and energy.

Ice melting provides an example of entropy increasing

Example of increasing entropy

Ice melting provides an example in which entropy increases in a small system, a thermodynamic system consisting of the surroundings (the warm room) and the entity of glass container, ice, water which has been allowed to reach thermodynamic equilibrium at the melting temperature of ice. In this system, some heat (δQ) from the warmer surroundings at 298 K (77 °F, 25 °C) transfers to the cooler system of ice and water at its constant temperature (T) of 273 K (32 °F, 0 °C), the melting temperature of ice. The entropy of the system, which is δQ/T, increases by δQ/273K. The heat δQ for this process is the energy required to change water from the solid state to the liquid state, and is called the enthalpy of fusion, i.e. ΔH for ice fusion.

It is important to realize that the entropy of the surrounding room decreases less than the entropy of the ice and water increases: the room temperature of 298 K is larger than 273 K and therefore the ratio, (entropy change), of δQ/298K for the surroundings is smaller than the ratio (entropy change), of δQ/273K for the ice and water system. This is always true in spontaneous events in a thermodynamic system and it shows the predictive importance of entropy: the final net entropy after such an event is always greater than was the initial entropy.

As the temperature of the cool water rises to that of the room and the room further cools imperceptibly, the sum of the δQ/T over the continuous range, “at many increments”, in the initially cool to finally warm water can be found by calculus. The entire miniature ‘universe’, i.e. this thermodynamic system, has increased in entropy. Energy has spontaneously become more dispersed and spread out in that ‘universe’ than when the glass of ice + water was introduced and became a 'system' within it.

Origins and uses

Originally, entropy was named to describe the "waste heat," or more accurately, energy losses, from heat engines and other mechanical devices which could never run with 100% efficiency in converting energy into work. Later, the term came to acquire several additional descriptions, as more was understood about the behavior of molecules on the microscopic level. In the late 19th century, the word "disorder" was used by Ludwig Boltzmann in developing statistical views of entropy using probability theory to describe the increased molecular movement on the microscopic level. That was before quantum behavior came to be better understood by Werner Heisenberg and those who followed. Descriptions of thermodynamic (heat) entropy on the microscopic level are found in statistical thermodynamics and statistical mechanics.

For most of the 20th century, textbooks tended to describe entropy as "disorder", following Boltzmann's early conceptualisation of the "motional" (i.e. kinetic) energy of molecules. More recently, there has been a trend in chemistry and physics textbooks to describe entropy as energy dispersal.^[3] Entropy can also involve the dispersal of particles, which are themselves energetic. Thus there are instances where both particles and energy disperse at different rates when substances are mixed together.

The mathematics developed in statistical thermodynamics were found to be applicable in other disciplines. In particular, information sciences developed the concept of information entropy where a constant replaces the temperature which is inherent in thermodynamic entropy.

Heat and entropy

At a microscopic level, kinetic energy of molecules is responsible for the temperature of a substance or a system. “Heat” is the kinetic energy of molecules being transferred: when motional energy is transferred from hotter surroundings to a cooler system, faster-moving molecules in the surroundings collide with the walls of the system which transfers some of their energy to the molecules of the system and makes them move faster.

• Molecules in a gas like nitrogen at room temperature at any instant are moving at an average speed of nearly 500 miles per hour (210 m/s), repeatedly colliding and therefore exchanging energy so that their individual speeds are always changing. Assuming an ideal-gas model, average kinetic energy increases linearly with temperature, so the average speed increases as the square root of temperature.
  • Thus motional molecular energy (‘heat energy’) from hotter surroundings, like faster-moving molecules in a flame or violently vibrating iron atoms in a hot plate, will melt or boil a substance (the system) at the temperature of its melting or boiling point. That amount of motional energy from the surroundings that is required for melting or boiling is called the phase-change energy, specifically the enthalpy of fusion or of vaporization, respectively. This phase-change energy breaks bonds between the molecules in the system (not chemical bonds inside the molecules that hold the atoms together) rather than contributing to the motional energy and making the molecules move any faster – so it does not raise the temperature, but instead enables the molecules to break free to move as a liquid or as a vapor.
  • In terms of energy, when a solid becomes a liquid or a vapor, motional energy coming from the surroundings is changed to ‘potential energy‘ in the substance (phase change energy, which is released back to the surroundings when the surroundings become cooler than the substance's boiling or melting temperature, respectively). Phase-change energy increases the entropy of a substance or system because it is energy that must be spread out in the system from the surroundings so that the substance can exist as a liquid or vapor at a temperature above its melting or boiling point. When this process occurs in a 'universe' that consists of the surroundings plus the system, the total energy of the 'universe' becomes more dispersed or spread out as part of the greater energy that was only in the hotter surroundings transfers so that some is in the cooler system. This energy dispersal increases the entropy of the 'universe'.

The important overall principle is that ”Energy of all types changes from being localized to becoming dispersed or spread out, if not hindered from doing so. Entropy (or better, entropy change) is the quantitative measure of that kind of a spontaneous process: how much energy has been transferred/T or how widely it has become spread out at a specific temperature.

Classical calculation of entropy

When entropy was first defined and used in 1865 the very existence of atoms was still controversial and there was no concept that temperature was due to the motional energy of molecules or that “heat” was actually the transferring of that motional molecular energy from one place to another. Entropy change, , was described in macroscopic terms that could be directly measured, such as volume, temperature, or pressure. However, today the classical equation of entropy, can be explained, part by part, in modern terms describing how molecules are responsible for what is happening:

• is the change in entropy of a system (some physical substance of interest) after some motional energy (“heat”) has been transferred to it by fast-moving molecules. So, .

• Then, , the quotient of the motional energy (“heat”) q that is transferred "reversibly" (rev) to the system from the surroundings (or from another system in contact with the first system) divided by T, the absolute temperature at which the transfer occurs.
  • “Reversible” or “reversibly” (rev) simply means that T, the temperature of the system, has to stay (almost) exactly the same while any energy is being transferred to or from it. That’s easy in the case of phase changes, where the system absolutely must stay in the solid or liquid form until enough energy is given to it to break bonds between the molecules before it can change to a liquid or a gas. For example in the melting of ice at 273.15 K, no matter what temperature the surroundings are – from 273.20 K to 500 K or even higher, the temperature of the ice will stay at 273.15 K until the last molecules in the ice are changed to liquid water, i.e., until all the hydrogen bonds between the water molecules in ice are broken and new, less-exactly fixed hydrogen bonds between liquid water molecules are formed. This amount of energy necessary for ice melting per mole has been found to be 6008 joules at 273 K. Therefore, the entropy change per mole is , or 22 J/K.
  • When the temperature isn't at the melting or boiling point of a substance no intermolecular bond-breaking is possible, and so any motional molecular energy (“heat”) from the surroundings transferred to a system raises its temperature, making its molecules move faster and faster. As the temperature is constantly rising, there is no longer a particular value of “T” at which energy is transferred. However, a "reversible" energy transfer can be measured at a very small temperature increase, and a cumulative total can be found by adding each of many small temperature intervals or increments. For example, to find the entropy change from 300 K to 310 K, measure the amount of energy transferred at dozens or hundreds of temperature increments, say from 300.00 K to 300.01 K and then 300.01 to 300.02 and so on, dividing the q by each T, and finally adding them all.
  • Calculus can be used to make this calculation easier if the effect of energy input to the system is linearly dependent on the temperature change, as in simple heating of a system at moderate to relatively high temperatures. Thus, the energy being transferred “per incremental change in temperature” (the heat capacity, ), multiplied by the integral of from to , is directly given by .

Introductory descriptions of entropy

Traditionally, 20th century textbooks have introduced entropy as order and disorder so that it provides "a measurement of the disorder or randomness of a system". It has been argued that ambiguities in the terms used (such as "disorder" and "chaos") contribute to widespread confusion and can hinder comprehension of entropy for most students. A more recent formulation associated with Frank L. Lambert describing entropy as energy dispersal.^[4]