From Wikipedia, the free encyclopedia

Simulated view of a black hole (center) in front of the Large Magellanic Cloud. Note the gravitational lensing effect, which produces two enlarged but highly distorted views of the Cloud. Across the top, the Milky Way disk appears distorted into an arc.
Hawking radiation is black body radiation that is predicted to be released by black holes, due to quantum effects near the event horizon.
It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974,[1] and sometimes also after Jacob Bekenstein, who predicted that black holes should have a finite, non-zero temperature and entropy.[2]
Hawking's work followed his visit to Moscow in 1973 where the Soviet scientists Yakov Zeldovich and Alexei Starobinsky showed him that according to the quantum mechanical uncertainty principle, rotating black holes should create and emit particles.[3] Hawking radiation reduces the mass and the energy of the black hole and is therefore also known as black hole evaporation. Because of this, black holes that lose more mass than they gain through other means are expected to shrink and ultimately vanish. Micro black holes (MBHs) are predicted to be larger net emitters of radiation than larger black holes and should shrink and dissipate faster.
In September 2010, a signal that is closely related to black hole Hawking radiation (see analog gravity) was claimed to have been observed in a laboratory experiment involving optical light pulses. However, the results remain unverified and debatable.[4][5] Other projects have been launched to look for this radiation within the framework of analog gravity. In June 2008, NASA launched the Fermi space telescope, which will search for the terminal gamma-ray flashes expected from evaporating primordial black holes. In the event that speculative large extra dimension theories are correct, CERN's Large Hadron Collider may be able to create micro black holes and observe their evaporation.[6][7][8][9][10]
Overview
Black holes are sites of immense gravitational attraction. Classically, the gravitation is so powerful that nothing, not even electromagnetic radiation (including light), can escape from the black hole. It is yet unknown how gravity can be incorporated into quantum mechanics. Nevertheless, far from the black hole the gravitational effects can be weak enough for calculations to be reliably performed in the framework of quantum field theory in curved spacetime. Hawking showed that quantum effects allow black holes to emit exact black body radiation, which is the average thermal radiation emitted by an idealized thermal source known as a black body. The electromagnetic radiation is as if it were emitted by a black body with a temperature that is inversely proportional to the black hole's mass.Physical insight into the process may be gained by imagining that particle-antiparticle radiation is emitted from just beyond the event horizon. This radiation does not come directly from the black hole itself, but rather is a result of virtual particles being "boosted" by the black hole's gravitation into becoming real particles.[11] As the particle-antiparticle pair was produced by the black hole's gravitational energy, the escape of one of the particles takes away some of the mass of the black hole.[12]
A slightly more precise, but still much simplified, view of the process is that vacuum fluctuations cause a particle-antiparticle pair to appear close to the event horizon of a black hole. One of the pair falls into the black hole while the other escapes. In order to preserve total energy, the particle that fell into the black hole must have had a negative energy (with respect to an observer far away from the black hole). By this process, the black hole loses mass, and, to an outside observer, it would appear that the black hole has just emitted a particle. In another model, the process is a quantum tunnelling effect, whereby particle-antiparticle pairs will form from the vacuum, and one will tunnel outside the event horizon.[11]
An important difference between the black hole radiation as computed by Hawking and thermal radiation emitted from a black body is that the latter is statistical in nature, and only its average satisfies what is known as Planck's law of black body radiation, while the former fits the data better. Thus thermal radiation contains information about the body that emitted it, while Hawking radiation seems to contain no such information, and depends only on the mass, angular momentum, and charge of the black hole (the no-hair theorem). This leads to the black hole information paradox.
However, according to the conjectured gauge-gravity duality (also known as the AdS/CFT correspondence), black holes in certain cases (and perhaps in general) are equivalent to solutions of quantum field theory at a non-zero temperature. This means that no information loss is expected in black holes (since the theory permits no such loss) and the radiation emitted by a black hole is probably the usual thermal radiation. If this is correct, then Hawking's original calculation should be corrected, though it is not known how (see below).
A black hole of one solar mass (M☉) has a temperature of only 60 nanokelvin (60 billionths of a kelvin); in fact, such a black hole would absorb far more cosmic microwave background radiation than it emits. A black hole of 4.5 × 1022 kg (about the mass of the Moon) would be in equilibrium at 2.7 kelvin, absorbing as much radiation as it emits. Yet smaller primordial black holes would emit more than they absorb and thereby lose mass.[11]
Trans-Planckian problem
The trans-Planckian problem is the observation that Hawking's original calculation requires talking about quantum particles in which the wavelength becomes shorter than the Planck length near the black hole's horizon. It is due to the peculiar behavior near a gravitational horizon where time stops as measured from far away. A particle emitted from a black hole with a finite frequency, if traced back to the horizon, must have had an infinite frequency there and a trans-Planckian wavelength.The Unruh effect and the Hawking effect both talk about field modes in the superficially stationary space-time that change frequency relative to other coordinates which are regular across the horizon. This is necessarily so, since to stay outside a horizon requires acceleration which constantly Doppler shifts the modes.
An outgoing Hawking radiated photon, if the mode is traced back in time, has a frequency which diverges from that which it has at great distance, as it gets closer to the horizon, which requires the wavelength of the photon to "scrunch up" infinitely at the horizon of the black hole. In a maximally extended external Schwarzschild solution, that photon's frequency only stays regular if the mode is extended back into the past region where no observer can go. That region doesn't seem to be observable and is physically suspect, so Hawking used a black hole solution without a past region which forms at a finite time in the past. In that case, the source of all the outgoing photons can be identified–it is a microscopic point right at the moment that the black hole first formed.
The quantum fluctuations at that tiny point, in Hawking's original calculation, contain all the outgoing radiation. The modes that eventually contain the outgoing radiation at long times are redshifted by such a huge amount by their long sojourn next to the event horizon, that they start off as modes with a wavelength much shorter than the Planck length. Since the laws of physics at such short distances are unknown, some find Hawking's original calculation unconvincing.[13][14][15][16][17][18]
The trans-Planckian problem is nowadays mostly considered a mathematical artifact of horizon calculations.[16][19] The same effect occurs for regular matter falling onto a white hole solution. Matter which falls on the white hole accumulates on it, but has no future region into which it can go. Tracing the future of this matter, it is compressed onto the final singular endpoint of the white hole evolution, into a trans-Planckian region. The reason for these types of divergences is that modes which end at the horizon from the point of view of outside coordinates are singular in frequency there. The only way to determine what happens classically is to extend in some other coordinates that cross the horizon.
There exist alternative physical pictures which give the Hawking radiation in which the trans-Planckian problem is addressed. The key point is that similar trans-Planckian problems occur when the modes occupied with Unruh radiation are traced back in time.[20] In the Unruh effect, the magnitude of the temperature can be calculated from ordinary Minkowski field theory, and is not controversial.
Emission process
Hawking radiation is required by the Unruh effect and the equivalence principle applied to black hole horizons. Close to the event horizon of a black hole, a local observer must accelerate to keep from falling in. An accelerating observer sees a thermal bath of particles that pop out of the local acceleration horizon, turn around, and free-fall back in. The condition of local thermal equilibrium implies that the consistent extension of this local thermal bath has a finite temperature at infinity, which implies that some of these particles emitted by the horizon are not reabsorbed and become outgoing Hawking radiation.[20]A Schwarzschild black hole has a metric
The field theory is defined by a local path integral, so if the boundary conditions at the horizon are determined, the state of the field outside will be specified. To find the appropriate boundary conditions, consider a stationary observer just outside the horizon at position
 .
.The local metric to lowest order is
 and
and  . The metric describes a frame that is accelerating to keep from falling into the black hole. The local acceleration diverges as
. The metric describes a frame that is accelerating to keep from falling into the black hole. The local acceleration diverges as  .
.The horizon is not a special boundary, and objects can fall in. So the local observer should feel accelerated in ordinary Minkowski space by the principle of equivalence. The near-horizon observer must see the field excited at a local inverse temperature
The gravitational redshift is by the square root of the time component of the metric. So for the field theory state to consistently extend, there must be a thermal background everywhere with the local temperature redshift-matched to the near horizon temperature:
 is the near-horizon position, near
is the near-horizon position, near  , so this is really
, so this is really ), the temperature is
), the temperature is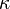 is the surface gravity of the horizon. So a black hole can only be in equilibrium with a gas of radiation at a finite temperature. Since radiation incident on the black hole is absorbed, the black hole must emit an equal amount to maintain detailed balance. The black hole acts as a perfect blackbody radiating at this temperature.
is the surface gravity of the horizon. So a black hole can only be in equilibrium with a gas of radiation at a finite temperature. Since radiation incident on the black hole is absorbed, the black hole must emit an equal amount to maintain detailed balance. The black hole acts as a perfect blackbody radiating at this temperature.In SI units, the radiation from a Schwarzschild black hole is black-body radiation with temperature
 is the reduced Planck constant, c is the speed of light, kB is the Boltzmann constant, G is the gravitational constant, and M is the mass of the black hole.
is the reduced Planck constant, c is the speed of light, kB is the Boltzmann constant, G is the gravitational constant, and M is the mass of the black hole.From the black hole temperature, it is straightforward to calculate the black hole entropy. The change in entropy when a quantity of heat dQ is added is
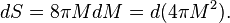 .
.
Black hole evaporation
When particles escape, the black hole loses a small amount of its energy and therefore some of its mass (mass and energy are related by Einstein's equation E = mc²).The power emitted by a black hole in the form of Hawking radiation can easily be estimated for the simplest case of a nonrotating, non-charged Schwarzschild black hole of mass
 . Combining the formulas for the Schwarzschild radius of the black hole, the Stefan–Boltzmann law of black-body radiation, the above formula for the temperature of the radiation, and the formula for the surface area of a sphere (the black hole's event horizon), equation derivation:
. Combining the formulas for the Schwarzschild radius of the black hole, the Stefan–Boltzmann law of black-body radiation, the above formula for the temperature of the radiation, and the formula for the surface area of a sphere (the black hole's event horizon), equation derivation:Stefan–Boltzmann constant:
 :
: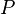 is the energy outflow,
is the energy outflow,  is the reduced Planck constant,
is the reduced Planck constant,  is the speed of light, and
is the speed of light, and  is the gravitational constant. It is worth mentioning that the above formula has not yet been derived in the framework of semiclassical gravity.
is the gravitational constant. It is worth mentioning that the above formula has not yet been derived in the framework of semiclassical gravity.The power in the Hawking radiation from a solar mass (
 ) black hole turns out to be a minuscule 9 × 10−29 watts. It is indeed an extremely good approximation to call such an object 'black'.
) black hole turns out to be a minuscule 9 × 10−29 watts. It is indeed an extremely good approximation to call such an object 'black'. (the initial mass of the black hole) to zero (complete evaporation), and over t from zero to
(the initial mass of the black hole) to zero (complete evaporation), and over t from zero to  :
: is the mass of the black hole.
is the mass of the black hole.The lower classical quantum limit for mass for this equation is equivalent to the Planck mass,
 .
.Planck mass quantum black hole Hawking radiation evaporation time:
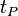 is the Planck time.
is the Planck time.For a black hole of one solar mass (
 = 1.98892 × 1030 kg), we get an evaporation time of 2.098 × 1067 years—much longer than the current age of the universe at 13.798 ± 0.037 x 109 years.[21]
= 1.98892 × 1030 kg), we get an evaporation time of 2.098 × 1067 years—much longer than the current age of the universe at 13.798 ± 0.037 x 109 years.[21]However, since the universe contains the cosmic microwave background radiation, in order for the black hole to dissipate, it must have a temperature greater than that of the present-day black-body radiation of the universe of 2.7 K = 2.3 × 10−4 eV. This implies that
 must be less than 0.8% of the mass of the Earth[22] - approximately the mass of the Moon.
must be less than 0.8% of the mass of the Earth[22] - approximately the mass of the Moon.Cosmic microwave background radiation universe temperature:
 is the total Earth mass.
is the total Earth mass.In common units,
Black hole evaporation has several significant consequences:
- Black hole evaporation produces a more consistent view of black hole thermodynamics, by showing how black holes interact thermally with the rest of the universe.
- Unlike most objects, a black hole's temperature increases as it radiates away mass. The rate of temperature increase is exponential, with the most likely endpoint being the dissolution of the black hole in a violent burst of gamma rays. A complete description of this dissolution requires a model of quantum gravity, however, as it occurs when the black hole approaches Planck mass and Planck radius.
- The simplest models of black hole evaporation lead to the black hole information paradox. The information content of a black hole appears to be lost when it dissipates, as under these models the Hawking radiation is random (it has no relation to the original information). A number of solutions to this problem have been proposed, including suggestions that Hawking radiation is perturbed to contain the missing information, that the Hawking evaporation leaves some form of remnant particle containing the missing information, and that information is allowed to be lost under these conditions.
Large extra dimensions
Formulae from the previous section are only applicable if laws of gravity are approximately valid all the way down to the Planck scale. In particular, for black holes with masses below Planck mass (~10−5 g), they result in unphysical lifetimes below Planck time (~10−43 s). This is normally seen as an indication that Planck mass is the lower limit on the mass of a black hole.In the model with large extra dimensions, values of Planck constants can be radically different, and formulas for Hawking radiation have to be modified as well. In particular, the lifetime of a micro black hole (with radius below the scale of extra dimensions) is given by (Equation (9) in [23]) & (Equation(25) (26) in [24])
 is the low energy scale (which could be as low as a few TeV), and n is the number of large extra dimensions. This formula is now consistent with black holes as light as a few TeV, with lifetimes on the order of "new Planck time" ~10−26 s.
is the low energy scale (which could be as low as a few TeV), and n is the number of large extra dimensions. This formula is now consistent with black holes as light as a few TeV, with lifetimes on the order of "new Planck time" ~10−26 s.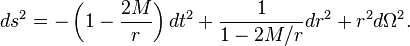

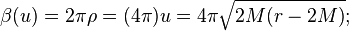







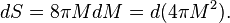 .
.


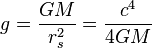

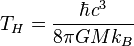
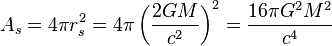




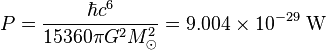



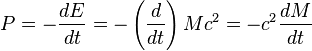







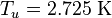


![P = 3.563 \, 45 \times 10^{32} \left[\frac{\mathrm{kg}}{M}\right]^2 \mathrm{W} \;](http://upload.wikimedia.org/math/b/3/0/b307eaf7dbd95b8f481e6157ecec7f95.png)
![t_\mathrm{ev} = 8.407 \, 16 \times 10^{-17} \left[\frac{M_0}{\mathrm{kg}}\right]^3 \mathrm{s}
\ \ \approx\ 2.66 \times 10^{-24} \left[\frac{M_0}{\mathrm{kg}}\right]^3 \mathrm{yr} \;](http://upload.wikimedia.org/math/5/c/8/5c88d81003c9522455c01af0acaae841.png)
![M_0 = 2.282 \, 71 \times 10^5 \left[\frac{t_\mathrm{ev}}{\mathrm{s}}\right]^{1/3} \mathrm{kg}
\ \ \approx\ 7.2 \times 10^7 \left[\frac{t_\mathrm{ev}}{\mathrm{yr}}\right]^{1/3} \mathrm{kg} \;](http://upload.wikimedia.org/math/e/d/8/ed81cf2b437f30c4ba0a27788b403357.png)