From Wikipedia, the free encyclopedia

Methane, CH4, in line-angle representation, showing four carbon-hydrogen single (σ) bonds in black, and the 3D shape of such tetrahedral molecules, with ~109° interior bond angles, in green. Methane is the simplest organic chemical and simplest hydrocarbon, and molecules can be built up conceptually from it by exchanging up to all 4 hydrogens with carbon or other atoms.
Organic chemistry is a chemistry subdiscipline involving the scientific study of the structure, properties, and reactions of organic compounds and organic materials, i.e., matter in its various forms that contain carbon atoms.[1][2] Study of structure includes using spectroscopy (e.g., NMR), mass spectrometry, and other physical and chemical methods to determine the chemical composition and constitution of organic compounds and materials. Study of properties includes both physical properties and chemical properties, and uses similar methods as well as methods to evaluate chemical reactivity, with the aim to understand the behavior of the organic matter in its pure form (when possible), but also in solutions, mixtures, and fabricated forms. The study of organic reactions includes probing their scope through use in preparation of target compounds (e.g., natural products, drugs, polymers, etc.) by chemical synthesis, as well as the focused study of the reactivities of individual organic molecules, both in the laboratory and via theoretical (in silico) study.
The range of chemicals studied in organic chemistry include hydrocarbons (compounds containing only carbon and hydrogen), as well as myriad compositions based always on carbon, but also containing other elements,[1][3][4] especially:
- oxygen, nitrogen, sulfur, phosphorus (these, included in many organic chemicals in biology) and the radiostable elements of the halogens.
- Group 1 and 2 organometallic compounds, i.e., involving alkali (e.g., lithium, sodium, and potassium) or alkaline earth metals (e.g., magnesium), or
- metalloids (e.g., boron and silicon) or other metals (e.g., aluminium and tin).
- transition metals (e.g., zinc, copper, palladium, nickel, cobalt, titanium, chromium, etc.).
Three representations of an organic compound, 5α-Dihydroprogesterone (5α-DHP), a steroid hormone. For molecules showing color, the carbon atoms are in black, hydrogens in gray, and oxygens in red. In the line angle representation, carbon atoms are implied at every terminus of a line and vertex of multiple lines, and hydrogen atoms are implied to fill the remaining needed valences (up to 4).
Finally, organic compounds form the basis of all earthly life and constitute a significant part of human endeavors in chemistry. The bonding patterns open to carbon, with its valence of four—formal single, double, and triple bonds, as well as various structures with delocalized electrons—make the array of organic compounds structurally diverse, and their range of applications enormous. They either form the basis of, or are important constituents of, many commercial products including pharmaceuticals; petrochemicals and products made from them (including lubricants, solvents, etc.); plastics; fuels and explosives; etc. As indicated, the study of organic chemistry overlaps with organometallic chemistry and biochemistry, but also with medicinal chemistry, polymer chemistry, as well as many aspects of materials science.[1]
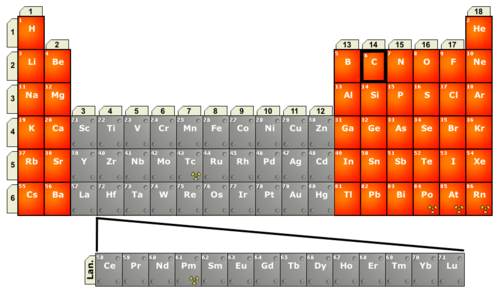
Periodic table of elements of interest in organic chemistry. The table illustrates all elements of current interest in modern organic and organometallic chemistry, indicating main group elements in orange, and transition metals and lanthanides (Lan) in grey.
History
Main article: History of chemistry
Before the nineteenth century, chemists generally believed that compounds obtained from living organisms were endowed with a vital force that distinguished them from inorganic compounds. According to the concept of vitalism (vital force theory), organic matter was endowed with a "vital force".[5] During the first half of the nineteenth century, some of the first systematic studies of organic compounds were reported. Around 1816 Michel Chevreul started a study of soaps made from various fats and alkalis. He separated the different acids that, in combination with the alkali, produced the soap. Since these were all individual compounds, he demonstrated that it was possible to make a chemical change in various fats (which traditionally come from organic sources), producing new compounds, without "vital force". In 1828 Friedrich Wöhler produced the organic chemical urea (carbamide), a constituent of urine, from the inorganic ammonium cyanate NH4CNO, in what is now called the Wöhler synthesis. Although Wöhler was always cautious about claiming that he had disproved the theory of vital force, this event has often been thought of as a turning point.[5]
In 1856 William Henry Perkin, while trying to manufacture quinine, accidentally manufactured the organic dye now known as Perkin's mauve. Through its great financial success, this discovery greatly increased interest in organic chemistry.[6]
The crucial breakthrough for organic chemistry was the concept of chemical structure, developed independently and simultaneously by Friedrich August Kekulé and Archibald Scott Couper in 1858.[7] Both men suggested that tetravalent carbon atoms could link to each other to form a carbon lattice, and that the detailed patterns of atomic bonding could be discerned by skillful interpretations of appropriate chemical reactions.
The pharmaceutical industry began in the last decade of the 19th century when the manufacturing of acetylsalicylic acid (more commonly referred to as aspirin) in Germany was started by Bayer.[8] The first time a drug was systematically improved was with arsphenamine (Salvarsan). Though numerous derivatives of the dangerous toxic atoxyl were examined by Paul Ehrlich and his group, the compound with best effectiveness and toxicity characteristics was selected for production.[citation needed]
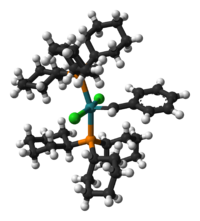
An example of an organometallic molecule, a catalyst called Grubbs' catalyst, as a ball-and-stick model based on an X-ray crystal structure.[9] The formula of the catalyst is often given as RuCl2(PCy3)2(=CHPh), where the ruthenium metal atom, Ru, is at very center in turquoise, carbons are in black, hydrogens in gray-white, chlorine in green, and phosphorus in orange. The metal ligand at the bottom is a tricyclohexyl phosphine, abbreviated PCy, and another of these appears at the top of the image (where its rings are obscuring one another). The group projecting out to the right has a metal-carbon double bond, as is known as an alkylidene. Robert Grubbs shared the 2005 Nobel prize in chemistry with Richard R. Schrock and Yves Chauvin for their work on the reactions such catalysts mediate, called olefin metathesis.
Early examples of organic reactions and applications were often serendipitous. The latter half of the 19th century however witnessed systematic studies of organic compounds, Illustrative is the development of synthetic indigo. The production of indigo from plant sources dropped from 19,000 tons in 1897 to 1,000 tons by 1914 thanks to the synthetic methods developed by Adolf von Baeyer. In 2002, 17,000 tons of synthetic indigo were produced from petrochemicals.[10]
In the early part of the 20th Century, polymers and enzymes were shown to be large organic molecules, and petroleum was shown to be of biological origin.
The multistep synthesis of complex organic compounds is called total synthesis. Total synthesis of complex natural compounds increased in complexity to glucose and terpineol. For example, cholesterol-related compounds have opened ways to synthesize complex human hormones and their modified derivatives. Since the start of the 20th century, complexity of total syntheses has been increased to include molecules of high complexity such as lysergic acid and vitamin B12.[11]
The development of organic chemistry benefited from the discovery of petroleum and the development of the petrochemical industry. The conversion of individual compounds obtained from petroleum into different compound types by various chemical processes led to the birth of the petrochemical industry, which successfully manufactured artificial rubbers, various organic adhesives, property-modifying petroleum additives, and plastics.
The majority of chemical compounds occurring in biological organisms are in fact carbon compounds, so the association between organic chemistry and biochemistry is so close that biochemistry might be regarded as in essence a branch of organic chemistry. Although the history of biochemistry might be taken to span some four centuries, fundamental understanding of the field only began to develop in the late 19th century and the actual term biochemistry was coined around the start of 20th century. Research in the field increased throughout the twentieth century, without any indication of slackening in the rate of increase, as may be verified by inspection of abstraction and indexing services such as BIOSIS Previews and Biological Abstracts, which began in the 1920s as a single annual volume, but has grown so drastically that by the end of the 20th century it was only available to the everyday user as an online electronic database.[12]
Characterization
Since organic compounds often exist as mixtures, a variety of techniques have also been developed to assess purity, especially important being chromatography techniques such as HPLC and gas chromatography. Traditional methods of separation include distillation, crystallization, and solvent extraction.Organic compounds were traditionally characterized by a variety of chemical tests, called "wet methods", but such tests have been largely displaced by spectroscopic or other computer-intensive methods of analysis.[13] Listed in approximate order of utility, the chief analytical methods are:
- Nuclear magnetic resonance (NMR) spectroscopy is the most commonly used technique, often permitting complete assignment of atom connectivity and even stereochemistry using correlation spectroscopy. The principal constituent atoms of organic chemistry - hydrogen and carbon - exist naturally with NMR-responsive isotopes, respectively 1H and 13C.
- Elemental analysis: A destructive method used to determine the elemental composition of a molecule. See also mass spectrometry, below.
- Mass spectrometry indicates the molecular weight of a compound and, from the fragmentation patterns, its structure. High resolution mass spectrometry can usually identify the exact formula of a compound and is used in lieu of elemental analysis. In former times, mass spectrometry was restricted to neutral molecules exhibiting some volatility, but advanced ionization techniques allow one to obtain the "mass spec" of virtually any organic compound.
- Crystallography is an unambiguous method for determining molecular geometry, the proviso being that single crystals of the material must be available and the crystal must be representative of the sample. Highly automated software allows a structure to be determined within hours of obtaining a suitable crystal.
Properties
Physical properties of organic compounds typically of interest include both quantitative andqualitative features. Quantitative information includes melting point, boiling point, and index of refraction. Qualitative properties include odor, consistency, solubility, and color.
Melting and boiling properties
Organic compounds typically melt and many boil. In contrast, while inorganic materials generally can be melted, many do not boil, tending instead to degrade. In earlier times, the melting point (m.p.) and boiling point (b.p.) provided crucial information on the purity and identity of organic compounds. The melting and boiling points correlate with the polarity of the molecules and their molecular weight. Some organic compounds, especially symmetrical ones, sublime, that is they evaporate without melting. A well-known example of a sublimable organic compound is para-dichlorobenzene, the odiferous constituent of modern mothballs. Organic compounds are usually not very stable at temperatures above 300 °C, although some exceptions exist.Solubility
Neutral organic compounds tend to be hydrophobic; that is, they are less soluble in water than in organic solvents. Exceptions include organic compounds that contain ionizable(which can be converted in ions) groups as well as low molecular weight alcohols, amines, and carboxylic acids where hydrogen bonding occurs. Organic compounds tend to dissolve in organic solvents. Solvents can be either pure substances like ether or ethyl alcohol, or mixtures, such as the paraffinic solvents such as the various petroleum ethers and white spirits, or the range of pure or mixed aromatic solvents obtained from petroleum or tar fractions by physical separation or by chemical conversion.Solubility in the different solvents depends upon the solvent type and on the functional groups if present.
Solid state properties
Various specialized properties of molecular crystals and organic polymers with conjugated systems are of interest depending on applications, e.g. thermo-mechanical and electro-mechanical such as piezoelectricity, electrical conductivity (see conductive polymers and organic semiconductors), and electro-optical (e.g. non-linear optics) properties. For historical reasons, such properties are mainly the subjects of the areas of polymer science and materials science.Nomenclature

The names of organic compounds are either systematic, following logically from a set of rules, or nonsystematic, following various traditions. Systematic nomenclature is stipulated by specifications from IUPAC. Systematic nomenclature starts with the name for a parent structure within the molecule of interest. This parent name is then modified by prefixes, suffixes, and numbers to unambiguously convey the structure. Given that millions of organic compounds are known, rigorous use of systematic names can be cumbersome. Thus, IUPAC recommendations are more closely followed for simple compounds, but not complex molecules. To use the systematic naming, one must know the structures and names of the parent structures. Parent structures include unsubstituted hydrocarbons, heterocycles, and monofunctionalized derivatives thereof.
Nonsystematic nomenclature is simpler and unambiguous, at least to organic chemists. Nonsystematic names do not indicate the structure of the compound. They are common for complex molecules, which includes most natural products. Thus, the informally named lysergic acid diethylamide is systematically named (6aR,9R)-N,N-diethyl-7-methyl-4,6,6a,7,8,9-hexahydroindolo-[4,3-fg] quinoline-9-carboxamide.
With the increased use of computing, other naming methods have evolved that are intended to be interpreted by machines. Two popular formats are SMILES and InChI.
Structural drawings
Organic molecules are described more commonly by drawings or structural formulas, combinations of drawings and chemical symbols. The line-angle formula is simple and unambiguous. In this system, the endpoints and intersections of each line represent one carbon, and hydrogen atoms can either be notated explicitly or assumed to be present as implied by tetravalent carbon. The depiction of organic compounds with drawings is greatly simplified by the fact that carbon in almost all organic compounds has four bonds, nitrogen three, oxygen two, and hydrogen one.Classification of organic compounds
Functional groups

The family of carboxylic acids contains a carboxyl (-COOH) functional group. Acetic acid, shown here, is an example.
The concept of functional groups is central in organic chemistry, both as a means to classify structures and for predicting properties. A functional group is a molecular module, and the reactivity of that functional group is assumed, within limits, to be the same in a variety of molecules. Functional groups can have decisive influence on the chemical and physical properties of organic compounds. Molecules are classified on the basis of their functional groups. Alcohols, for example, all have the subunit C-O-H. All alcohols tend to be somewhat hydrophilic, usually form esters, and usually can be converted to the corresponding halides. Most functional groups feature heteroatoms (atoms other than C and H). Organic compounds are classified according to functional groups, alcohols, carboxylic acids, amines, etc.
Aliphatic compounds
The aliphatic hydrocarbons are subdivided into three groups of homologous series according to their state of saturation:- paraffins, which are alkanes without any double or triple bonds,
- olefins or alkenes which contain one or more double bonds, i.e. di-olefins (dienes) or poly-olefins.
- alkynes, which have one or more triple bonds.
Both saturated (alicyclic) compounds and unsaturated compounds exist as cyclic derivatives. The most stable rings contain five or six carbon atoms, but large rings (macrocycles) and smaller rings are common. The smallest cycloalkane family is the three-membered cyclopropane ((CH2)3). Saturated cyclic compounds contain single bonds only, whereas aromatic rings have an alternating (or conjugated) double bond. Cycloalkanes do not contain multiple bonds, whereas the cycloalkenes and the cycloalkynes do.
Aromatic compounds
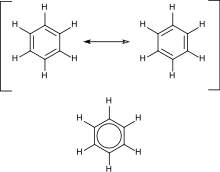
Benzene is one of the best-known aromatic compounds as it is one of the simplest and most stable aromatics.
Aromatic hydrocarbons contain conjugated double bonds. This means that every carbon atom in the ring is sp2 hybridized, allowing for added stability. The most important example is benzene, the structure of which was formulated by Kekulé who first proposed the delocalization or resonance principle for explaining its structure. For "conventional" cyclic compounds, aromaticity is conferred by the presence of 4n + 2 delocalized pi electrons, where n is an integer. Particular instability (antiaromaticity) is conferred by the presence of 4n conjugated pi electrons.
Heterocyclic compounds
The characteristics of the cyclic hydrocarbons are again altered if heteroatoms are present, which can exist as either substituents attached externally to the ring (exocyclic) or as a member of the ring itself (endocyclic). In the case of the latter, the ring is termed a heterocycle. Pyridine and furan are examples of aromatic heterocycles while piperidine and tetrahydrofuran are the corresponding alicyclic heterocycles. The heteroatom of heterocyclic molecules is generally oxygen, sulfur, or nitrogen, with the latter being particularly common in biochemical systems.Examples of groups among the heterocyclics are the aniline dyes, the great majority of the compounds discussed in biochemistry such as alkaloids, many compounds related to vitamins, steroids, nucleic acids (e.g. DNA, RNA) and also numerous medicines. Heterocyclics with relatively simple structures are pyrrole (5-membered) and indole (6-membered carbon ring).
Rings can fuse with other rings on an edge to give polycyclic compounds. The purine nucleoside bases are notable polycyclic aromatic heterocycles. Rings can also fuse on a "corner" such that one atom (almost always carbon) has two bonds going to one ring and two to another. Such compounds are termed spiro and are important in a number of natural products.
Polymers

This swimming board is made of polystyrene, an example of a polymer.
One important property of carbon is that it readily forms chains, or networks, that are linked by carbon-carbon (carbon to carbon) bonds. The linking process is called polymerization, while the chains, or networks, are called polymers. The source compound is called a monomer.
Two main groups of polymers exist: synthetic polymers and biopolymers. Synthetic polymers are artificially manufactured, and are commonly referred to as industrial polymers.[14] Biopolymers occur within a respectfully natural environment, or without human intervention.
Since the invention of the first synthetic polymer product, bakelite, synthetic polymer products have frequently been invented.[citation needed]
Common synthetic organic polymers are polyethylene (polythene), polypropylene, nylon, teflon (PTFE), polystyrene, polyesters, polymethylmethacrylate (called perspex and plexiglas), and polyvinylchloride (PVC).[citation needed]
Both synthetic and natural rubber are polymers.[citation needed]
Varieties of each synthetic polymer product may exist, for purposes of a specific use. Changing the conditions of polymerization alters the chemical composition of the product and its properties. These alterations include the chain length, or branching, or the tacticity.[citation needed]
With a single monomer as a start, the product is a homopolymer.[citation needed]
Secondary component(s) may be added to create a heteropolymer (co-polymer) and the degree of clustering of the different components can also be controlled.[citation needed]
Physical characteristics, such as hardness, density, mechanical or tensile strength, abrasion resistance, heat resistance, transparency, colour, etc. will depend on the final composition.[citation needed]
Biomolecules
Biomolecular chemistry is a major category within organic chemistry which is frequently studied by biochemists. Many complex multi-functional group molecules are important in living organisms. Some are long-chain biopolymers, and these include peptides, DNA, RNA and the polysaccharides such as starches in animals and celluloses in plants. The other main classes are amino acids (monomer building blocks of peptides and proteins), carbohydrates (which includes the polysaccharides), the nucleic acids (which include DNA and RNA as polymers), and the lipids. In addition, animal biochemistry contains many small molecule intermediates which assist in energy production through the Krebs cycle, and produces isoprene, the most common hydrocarbon in animals. Isoprenes in animals form the important steroid structural (cholesterol) and steroid hormone compounds; and in plants form terpenes, terpenoids, some alkaloids, and a class of hydrocarbons called biopolymer polyisoprenoids present in the latex of various species of plants, which is the basis for making rubber.
Small molecules
In pharmacology, an important group of organic compounds is small molecules, also referred to as 'small organic compounds'. In this context, a small molecule is a small organic compound that is biologically active, but is not a polymer. In practice, small molecules have a molar mass less than approximately 1000 g/mol.
Fullerenes
Fullerenes and carbon nanotubes, carbon compounds with spheroidal and tubular structures, have stimulated much research into the related field of materials science. The first fullerene was discovered in 1985 by Sir Harold W. Kroto (one of the authors of this article) of the United Kingdom and by Richard E. Smalley and Robert F. Curl, Jr., of the United States. Using a laser to vaporize graphite rods in an atmosphere of helium gas, these chemists and their assistants obtained cagelike molecules composed of 60 carbon atoms (C60) joined together by single and double bonds to form a hollow sphere with 12 pentagonal and 20 hexagonal faces—a design that resembles a football, or soccer ball. In 1996 the trio was awarded the Nobel Prize for their pioneering efforts. The C60 molecule was named buckminsterfullerene (or, more simply, the buckyball) after the American architect R. Buckminster Fuller, whose geodesic dome is constructed on the same structural principles. The elongated cousins of buckyballs, carbon nanotubes, were identified in 1991 by Iijima Sumio of Japan.Others
Organic compounds containing bonds of carbon to nitrogen, oxygen and the halogens are not normally grouped separately. Others are sometimes put into major groups within organic chemistry and discussed under titles such as organosulfur chemistry, organometallic chemistry, organophosphorus chemistry and organosilicon chemistry.Organic synthesis

A synthesis designed by E.J. Corey for oseltamivir (Tamiflu). This synthesis has 11 distinct reactions.
Synthetic organic chemistry is an applied science as it borders engineering, the "design, analysis, and/or construction of works for practical purposes". Organic synthesis of a novel compound is a problem solving task, where a synthesis is designed for a target molecule by selecting optimal reactions from optimal starting materials. Complex compounds can have tens of reaction steps that sequentially build the desired molecule. The synthesis proceeds by utilizing the reactivity of the functional groups in the molecule. For example, a carbonyl compound can be used as a nucleophile by converting it into an enolate, or as an electrophile; the combination of the two is called the aldol reaction. Designing practically useful syntheses always requires conducting the actual synthesis in the laboratory. The scientific practice of creating novel synthetic routes for complex molecules is called total synthesis.
Strategies to design a synthesis include retrosynthesis, popularized by E.J. Corey, starts with the target molecule and splices it to pieces according to known reactions. The pieces, or the proposed precursors, receive the same treatment, until available and ideally inexpensive starting materials are reached. Then, the retrosynthesis is written in the opposite direction to give the synthesis. A "synthetic tree" can be constructed, because each compound and also each precursor has multiple syntheses.
Organic reactions
Organic reactions are chemical reactions involving organic compounds. Many of these reactions are associated with functional groups. The general theory of these reactions involves careful analysis of such properties as the electron affinity of key atoms, bond strengths and steric hindrance. These factors can determine the relative stability of short-lived reactive intermediates, which usually directly determine the path of the reaction.The basic reaction types are: addition reactions, elimination reactions, substitution reactions, pericyclic reactions, rearrangement reactions and redox reactions. An example of a common reaction is a substitution reaction written as:
- Nu− + C-X → C-Nu + X−
The number of possible organic reactions is basically infinite. However, certain general patterns are observed that can be used to describe many common or useful reactions. Each reaction has a stepwise reaction mechanism that explains how it happens in sequence—although the detailed description of steps is not always clear from a list of reactants alone.
The stepwise course of any given reaction mechanism can be represented using arrow pushing techniques in which curved arrows are used to track the movement of electrons as starting materials transition through intermediates to final products.








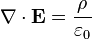 (
(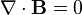 (
(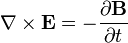 (
( (
( is the charge density, which can (and often does) depend on time and position,
is the charge density, which can (and often does) depend on time and position, 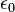 is the
is the 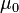 is the
is the 
 (current-free)
(current-free) (charge-free)
(charge-free)
 of each medium:
of each medium:
 of each medium:
of each medium:


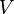 is a solution to
is a solution to  is also a solution to Maxwell's equations and no experiment can distinguish between these two solutions. In other words the laws of physics governing electricity and magnetism (that is, Maxwell equations) are invariant under gauge transformation.
is also a solution to Maxwell's equations and no experiment can distinguish between these two solutions. In other words the laws of physics governing electricity and magnetism (that is, Maxwell equations) are invariant under gauge transformation.
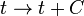 , rotations, etc., but become completely arbitrary, so that for example one can define an entirely new timelike coordinate according to some arbitrary rule such as
, rotations, etc., but become completely arbitrary, so that for example one can define an entirely new timelike coordinate according to some arbitrary rule such as 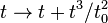 , where
, where 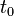 has units of time, and yet
has units of time, and yet